轨道坐标系到星固坐标系的四元数转换方法

李萌萌，王潜心，李怀展，饶鹏文

(1.中国矿业大学 国土环境与灾害监测国家测绘地理信息局重点实验室，江苏 徐州 221116；2.中国矿业大学 太空采矿国际研究中心，江苏 徐州 221116)

0 引 言

能源是人类活动的物质基础，是整个世界发展和经济增长的最基本驱动力。社会的不断发展导致人类面临越来越严峻的资源危机。随着宇宙探测时代的到来，人们认识到太空是人类赖以生存的资源宝库[1]，仅就太阳系而言，月球、火星、小行星等天体上具有丰富的稀有金属和其他矿产资源[2]，类木行星和彗星上有丰富的氢能资源[3]。为了解决地球矿产资源面临枯竭的难题，开发与利用丰富的太空资源势在必行。

开展深空探测并绘制星体表面资源分布图是太空采矿的前提和基础，目前资源分布图的绘制一般是采用遥感影像制图来完成的[4]，然而利用深空探测器直接获取的遥测影像通常是在轨道坐标系下[5]，因此需要转换到星固坐标系下，以便绘制星体表面矿产资源分布图。轨道坐标系到星固坐标系的转换是采用两步转换法完成的，第一步是从轨道坐标系转换到星体天球坐标系，第二步是从星体天球坐标系转换到星固坐标系。对于轨道坐标系到星体天球坐标系的转换，刘洋等[6]介绍了两种轨道坐标系到地心天球坐标系的转换方法，分别为直接转换法和间接转换法，并对两种转换方法对比分析，得出直接转换法优于间接转换法的结论。对于星体天球坐标系到星固坐标系的转换，只需要通过天体的定向参数信息即可完成转换，转换参数一般由相关组织利用高精度观测资料计算得到，比如月心天球坐标系到月固坐标系的转换参数从JPL(jet propulsion laboratory)发布的行星星历文件中获取，转换方法由W.M.Folkner 等[7]详细给出。但是两步转换过程中，转换参数的获取相对比较麻烦，当探测器在较低轨道运行时，通过星体表面测站可以获取探测器在星固坐标系下的轨道数据，此时可采用一步转换法完成轨道坐标系到星固坐标系的转换，一步转换法是通过空间向量旋转来完成转换，而四元数是高效的空间向量方位表示及旋转操作的工具，且四元数叉乘的效率明显高于矩阵做同样的操作，基于此，窦长勇等[8]应用四元数方法实现质心轨道坐标系到地固坐标系的转换，并证明该方法的可用性和有效性，但是该方法仅能够达到两步转换法同等精度，且该方法的转换精度受星固坐标系下探测器的轨道数据精度影响较大。为提高基于四元数的轨道坐标系到星固坐标系转换精度，解决星固坐标系下探测器的轨道数据中存在退化数据影响坐标转换精度的问题，本文采用基于四元数的三维坐标转换解析解法实现轨道坐标系到星固坐标系的转换，利用STK软件仿真月面反射器和月球探测器的数据通过3种方法实现坐标转换，并对比分析3种方法的精度和适用性。

1 坐标系的定义

本文主要研究从探测器轨道坐标系到星固坐标系的坐标转换方法，所涉及的坐标系有3个：探测器轨道坐标系OCS、星体天球坐标系ACCS和星固坐标系AFCS，如图1所示。

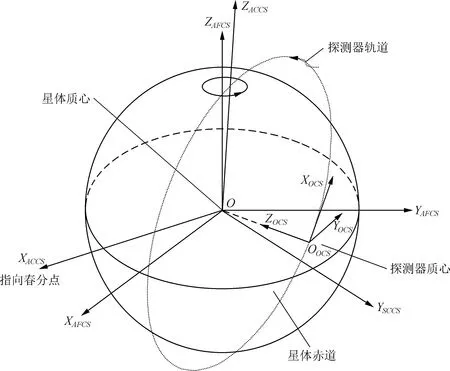
图1 深空探测器轨道坐标系、星体天球坐标系、星固坐标系示意图Fig.1 Schematic diagram of deep space probeorbit coordinate system,astral celestial coordinatesystem and astral fixed coordinate system

探测器轨道坐标系OCS：原点位于探测器的质心OOCS，ZOCS为指向星体的质心O，YOCS为ZOCS和探测器瞬时速度的叉乘积，其方向和探测器的瞬时角动量矢量相反。XOCS为YOCS和ZOCS的叉乘积[8]。

星体天球坐标系ACCS：原点位于星体的质心O，参考平面为平行于地球的J2000平赤道，ZACCS为从原点O指向J2000的平均北天极点，XACCS为从原点指向J2000的平均春分点，YACCS为ZACCS轴和XACCS的叉乘积[9]。

星固坐标系AFCS：原点为星体的质心O，参考平面为星体的赤道面，XAFCS为指向星体的起始子午线方向。ZAFCS沿星体自转角动量方向，该坐标系为右手坐标系。

2 两步转换法

两步转换法的基本思想是：首先将被探测星体表面点从轨道坐标系利用探测器在星体天球坐标系下的位置和速度转换到星体天球坐标系，再从星体天球坐标系利用星体的定向参数转换到星固坐标系。

2.1 从探测器轨道坐标系到星体天球坐标系的 转换

探测器轨道坐标系到星体天球坐标系转换过程的旋转矩阵为

(1)

式中,b1,b2和b3由式(2)求得

(2)

其中,PACCS和VACCS为探测器在星体天球坐标系下的位置和速度矢量[8]。

从轨道坐标系到星体天球坐标系的转换公式为

(3)

2.2 从星体天球坐标系到星固坐标系的转换

从星体天球坐标系到星固坐标系的旋转矩阵为

(4)

从星体天球坐标系到星固坐标系的转换公式为

(5)

2.3 星体定向参数的获取

以月球为例，月球的定向参数是物理天平动的3个欧拉角，利用行星星历文件通过切比雪夫插值可以得到，本文采用的是JPL发布的DE430星历文件。

2.3.1 行星星历文件的结构

对于DE430的ASCⅡ星历文件，星历数据的主要部分被分割成100 a跨度的子文件块，每个子文件块包含了若干个32 d的星历数据记录。每个星历数据记录的前两个数据分别为该星历数据记录的起始儒略日和结束儒略日，其余的数据为天体位置、地球章动、月球天平动的切比雪夫插值多项式系数[9]。

32 d的星历数据记录通过包含在ASCⅡ头文件的GROUP 1050中的标志指示器来区别。标志指示器由3组，每组13个数据组成，这13列整数提供了13个插值项目对应的切比雪夫多项式系数在星历数据记录中的位置、次序和时间跨度[10]。对应的13个项目分别为水星、金星、地月系质心、火星、木星、土星、天王星、海王星、冥王星、月球、太阳、地球章动和月球天平动[11]。DE430历表标志指示器的结构如表1所示。

表1 DE430历表标志指示器结构

表1中，标志指示器包含13个插值项目，对于第i个插值项目，第1行第i列指出了该项目在星历数据记录中切比雪夫系数的起始位置，第2行第i列表示每个组成部分的切比雪夫系数的数目，第3行第i列指出在此星历数据记录中该项目在星历数据由几个部分组成。第13列数据代表月球天平动的数据，第13列第1行数据899表示月球天平动的切比雪夫多项式系数从星历数据记录的第899个数据开始，第2行数据10表示每个子数据块中月球天平动的3个欧拉角分别含有10个切比雪夫多项式系数，第3行数据4表示数据块被分为4个子数据块，每个小块的时间跨度为8 d[9]。

2.3.2 切比雪夫插值多项式

(6)

式中：Tk(t)为第一类切比雪夫多项式；ak切比雪夫多项式的系数。

t是一个标准化的时刻，其值为

(7)

式中：T为当前的儒略日数；T0为星历数据记录中该系数节点开始处的儒略日数；ΔT为星历数据记录中每个小块的时间跨度[10]。

3 一步转换法

该方法根据轨道坐标系和星固坐标系的定义，直接利用在星固坐标系下探测器的绝对位置和绝对速度矢量求解旋转矩阵和平移参量，完成轨道坐标系到星固坐标系的转换。该方法与两步转换法中的第一步相似，只是计算转换参数的数据是探测器在星固坐标系下的位置和速度矢量，具体公式见2.1节。

4 基于四元数的解析法

基于四元数的解析法具有存储空间较小、计算效率较高、对退化数据的鲁棒性较好等优点。而遥感影像制图中利用探测器获取的遥测影像点位较多，因此需要进行坐标转换的点位较多，存储空间较大；且星固坐标系下探测器的位置和速度矢量精度较低，将会对坐标转换的精度产生一定的影响。因此，基于四元数的解析法应用于探测器轨道坐标系到星固坐标系的转换可以提高计算效率，并能够对退化数据进行抗差，提高转换精度。四元数解析法应用定义在星固坐标系下探测器的位置和速度矢量，求解星固坐标系下轨道坐标轴的矢量表达，以轨道坐标轴作为公共矢量建立矢量转换模型，用单位四元数来表达旋转矩阵，根据最小二乘原理和单位四元数的性质构建拉格朗日函数求得单位四元数，完成轨道坐标系到星固坐标系的转换。

根据轨道坐标系的定义，轨道坐标轴在星固坐标系下表示为

(8)

轨道坐标轴在其自身坐标系中分别表示为zocs=(0,0,1)，yocs=(0,1,0)，xocs=(1,0,0)。建立矢量转换模型为

(9)

式中：λ为尺度参数；R为旋转矩阵。

实四元数是一种四元矢量，可以表示为[12-13]

q=iq1+jq2+kq3+q4=q+q4，

(10)

(11)

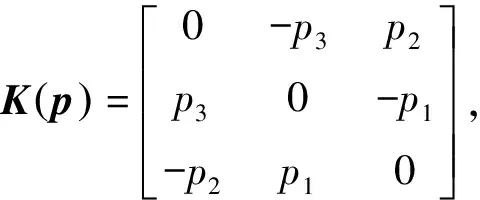
(12)

式中，记

(13)

(14)

式中，I为单位矩阵。

旋转矩阵与四元数的关系为[16]

(15)

转换模型可以表示为

由于轨道坐标轴在其自身坐标系中的矢量表示不存在误差，只考虑轨道坐标轴在星固坐标系下的矢量表示存在误差，可得

Pi+εi=λW(q)TQ(q)pi。

(17)

根据最小二乘的准则，选择合适的参数，式(18)可取得最小值[17]

[λW(q)TQ(q)pi-Pi]。

(18)

由于qTq-1=0，可构建拉格朗日函数：

Q(q)pi-Pi]+β1(qTq-1)，

(19)

式中，β1为拉格朗日乘子。

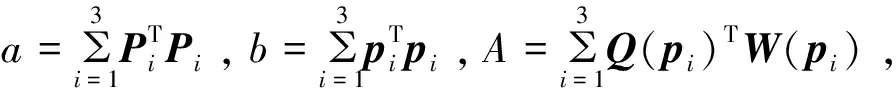
l′=a+bλ2-λqT(A+AT)q+β1(qTq-1)，

(21)

(22)

(23)

(24)

对式(22)求转置,可得

2β1q-2(A+AT)q=0。

(25)

Q(pi)TW(pi)是对称矩阵，所以A是对称矩阵。式(25)可以写为

2β1q-4Aq=0⟹2Aq=β1q⟹Dq=β1q，

(26)

式中：β1和q是D的特征值和特征向量，矩阵D有4个实特征值和正交实特征向量。

对式(26)左乘qT得

β1-2qTAq=0，

(27)

将式(27)代入误差函数l,得

l=a+b-β1，

(28)

因此,当β1为最大特征值时，l取得最小值，q为矩阵D的最大特征值对应的特征向量。

由式(25)可知

(29)

由此完成轨道坐标系与星固坐标系之间的转换。两坐标系之间的转换关系：

该方法采用探测器轨道坐标轴矢量作为公共矢量进行转换，仅在轨道坐标系轴附近方向的点位转换精度较高，所以对于星固坐标系下探测器轨道数据精度较高的情况，该方法适用于探测器正下方的小范围区域。

5 仿真与分析

5.1 获取仿真数据与实验过程

为获取仿真数据，本文首先利用STK软件建立1个月球场景，在月球场景中插入4个月面反射器Apollo 11，Apollo 14，Apollo 15，Luna 21，并在月面反射器的正上方分别插入1个低轨探测器。利用STK软件的可见性分析功能分别分析4个月球探测器与4个月面反射器的可见性，获取特定时刻月面反射器在探测器轨道坐标系下的三维坐标，并利用STK软件获取特定时刻探测器在月心天球坐标系和月固坐标系下的位置和速度。

通过STK软件获取月心天球坐标系和月固坐标系下探测器的位置和速度矢量，以及探测器轨道坐标系下月面反射器的三维坐标。由于实际场景中月固坐标系下探测器轨道数据的精度较低，且探测器轨道数据精度对3种坐标转换方法精度的影响较大，因此为了更准确地对比实际场景中一步转换法和四元数解析法的转换精度，在月固坐标系下探测器的位置和速度矢量数据中增加一定的误差。分别利用STK软件仿真的数据通过3种坐标转换方法实现月面反射器从轨道坐标系到月固坐标系的转换，并利用包含一定误差的月固坐标系下探测器的轨道数据通过一步转换法和四元数解析法实现月面反射器从轨道坐标系到月固坐标系的转换。最后，对3种方法的转换结果与实际坐标的点位误差进行对比分析，得出3种方法的适用范围。

5.2 仿真结果与分析

对3种坐标转换方法的转换结果与月面反射器月固坐标的点位误差进行对比分析，得出3种方法的适用范围。为了直观地对3种方法的精度进行对比，给出利用3种方法实现月面反射器从轨道坐标系到月固坐标系转换的点位误差对比图(图2)。

图2 利用3种方法实现月面反射器从轨道坐标系到月固坐标系转换的点位误差对比图

由图2可知：(1)使用STK软件仿真的数据进行坐标转换时，两步转换法和一步转换法的转换误差不随月面点与星下点距离的变化而变化；四元数解析法的转换误差随月面点与星下点距离的变化而变化；当月面点与星下点的距离最近时，四元数解析法和一步转换法的转换误差相等，均小于两步转换法；随着月面点与星下点距离的逐渐增大，四元数解析法的转换误差比一步转换法的误差大，但仍小于两步转换法，直到月面点与星下点的距离达到阈值，两步转换法的转换误差小于四元数解析法。(2)使用增加一定误差的月固坐标系下探测器轨道数据进行坐标转换时，四元数解析法的转换精度优于一步转换法。

6 结 论

(1)本文详细给出常用的两步转换法和一步转换法的公式，针对两步转换法和一步转换法的精度受探测器轨道数据精度影响较大的弊端，提出四元数解析法，并详细推导该方法的坐标转换公式，利用仿真数据对比了四元数解析法、两步转换法和一步转换法的点位误差。

(2)根据3种方法的坐标转换点位误差对比情况，分析3种坐标转换方法的适用范围，结果表明3种方法均有其特定的适用范围，而本文提出的四元数解析法对于星固坐标系下探测器轨道数据精度较低，且探测器位于点位过顶区域附近的情况具有较高的精度。