多种环境下GNSS-RTK监测噪声特性分析

陈 刚，于丽娜

（1.中海石油技术检测有限公司，天津 300452；2.天津大学 建筑工程学院，天津 300350）

0 引言

新兴的全球卫星导航系统（global navigation satellite system, GNSS），由于具备自动化程度高，受环境影响小，支持全天候监测，可直接获取三维坐标信息等诸多优势，目前已广泛应用于遥感、测绘、工程结构变形监测等诸多领域。实时动态差分（real time kinematic, RTK）是一种基于载波相位双差模型进行定位的技术，RTK模式下，GNSS监测具有较高的精度[1-3]。随着星座系统的完善和设备采样频率的提升，GNSS-RTK技术能够提供更加安全可靠的监测数据。

然而，由于多路径误差在测站间不具相关性，无法通过差分方式消除，多路径效应成为影响GNSS-RTK监测精度的主要因素。基于多路径误差的周期重复特性，人们尝试构建误差修正模型进行恒星日滤波，对削弱多路径效应具有良好效果[4-6]。但是，在实际的工程监测中，周边环境随时可能发生改变，导致GNSS-RTK监测难以获取精准的误差修正模型。此外，GNSS-RTK监测精度还受仪器内部噪声的干扰。研究表明，仪器内部噪声呈现明显的高斯白噪声特性[7]。文献[8-9]通过经验模态分解（empirical mode decomposition, EMD）算法，获取固有模式函数（intrinsic mode function, IMF），基于白噪声分量的能量密度与其平均周期的乘积为常量这一特性，筛选IMF分量进而实现白噪声与多路径误差分离，这为本次研究提供了参考借鉴。为了提升GNSS-RTK监测精度，需要充分了解其误差特性，并考虑监测环境的影响。为此，本文提出一种改进的噪声分解算法，对GSSS-RTK监测噪声信号进行分解，从而实现多路径误差与仪器内部噪声分离。

本文利用改进的自适应噪声完备集合经验模态分解（complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN）算法联合平均周期图法，对不同环境下GNSS-RTK监测稳定性试验数据进行噪声特性分析。首先介绍了联合算法的基本原理和应用流程；然后应用矩阵实验室（matrix laboratory, MATLAB）软件建立仿真信号， 验证改进CEEMDAN 算法的噪声分离效果；在此基础上，对4种环境（水域，水泥地，草地，变电站）GNSS-RTK稳定性试验数据进行处理和分析，进而评估不同环境下 GNSS-RTK的监测噪声特性。

2 改进 CEEMDAN算法联合平均周期图法基本原理

2.1 CEEMDAN算法基本原理

CEEMDAN算法是对EMD经典算法的最新发展，通过添加自适应白噪声并且计算唯一残余分量，解决了 EMD分解中模态混叠、白噪声污染、附加模态[10-14]等问题，其基本原理如下：

1）对原始信号x(t)添加N次白噪声ε0ωi(t)（i= 1,2,…，N） ，并进行 EMD分解，得到第一组IMF分量，可表示为

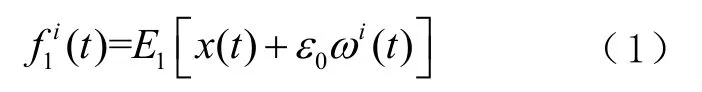
式中：E1[·]表示第一次EMD分解得到的IMF分量；ω(t)为正态白噪声；ε0为第一次添加的白噪声幅值系数。

2）对第一组 IMF分量进行平均处理，成为CEEMDAN分解的第一阶IMF分量，即

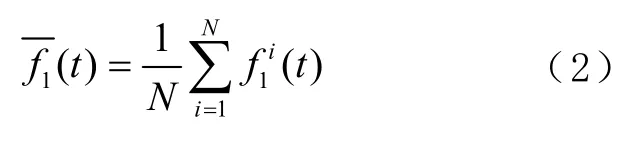
式中，f1i(t)为第一组IMF分量。

3）第一个残余信号可表示为

4）对r1(t)添加新的白噪声1E1i(t)εω，并继续分解，得到第二阶IMF分量，即

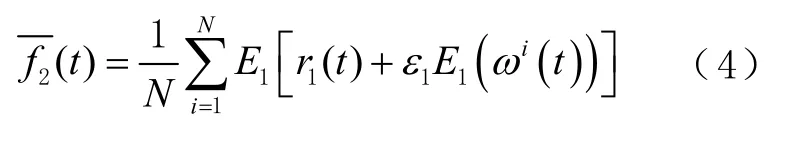
5）以此类推，得到第j个残余信号，即

6）第j+1阶IMF分量可表示为

7）循环步骤4）、步骤5），直到分解完成，得到最终的残余分量，即

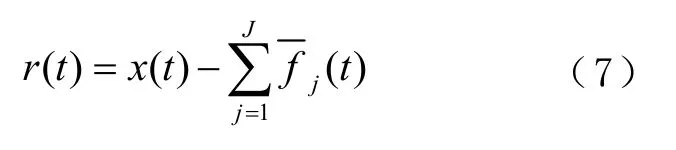
式中，J为IMF分量总阶数。

2.2 基于相关系数和有效系数重构IMF分量

在充分考虑 GNSS-RTK监测噪声特性的基础上，提出基于有效系数和相关系数相结合的方法，来筛选含有高斯白噪声的IMF分量。

1）相关系数。相关系数是用以反映两个变量间相关程度的统计指标，可表示为

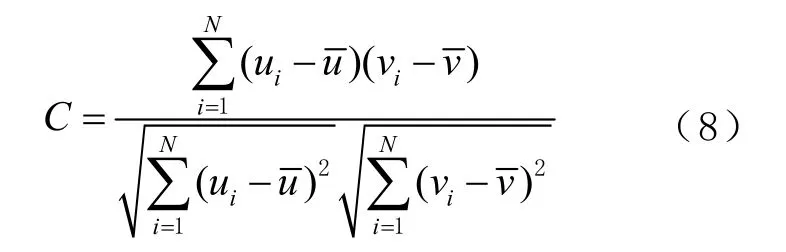
式中：N为数据长度；u,v代表两个独立变量（信号）；分别为变量u,v的平均值，可分别表示为

信号经CEEMDAN分解后，得到一系列按频率由高到低排列的 IMF分量。根据高斯白噪声的随机特性，白噪声主导的 IMF分量与原始不含噪序列的相关程度较低，因而可根据 IMF分量与原始信号的相关系数阈值判定其是否为白噪声主导分量。参考文献[15]，阈值可取

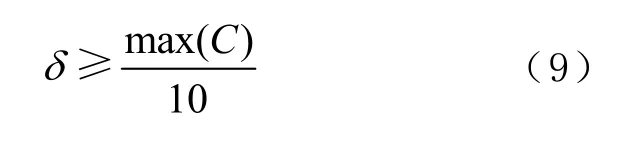
式中，C为相关系数。

2）有效系数。将能量密度与平均周期的乘积定义为能量系数，其表达式为

式中：D为能量密度；为平均周期。

能量密度的表达式为

式中：M为信号长度；fl(n)为第l个 IMF分量的幅值。

平均周期的表达式为

式中，Ol为第l个IMF分量的极值点个数。

白噪声主导的IMF分量，其能量系数为常量。根据这一特性，构造有效系数作为判定标准筛选白噪声[16]。有效系数可表示为

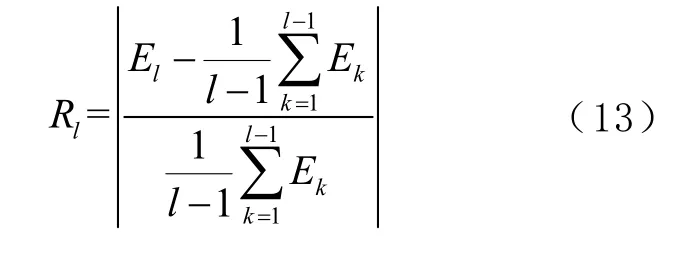
当Rl≥1时，说明第l个IMF分量对应的能量系数，较前l-1项 IMF 分量能量系数的平均值成倍增大，表明前l-1项 IMF 分量的能量系数为常量，即白噪声分量。

3）相关系数和有效系数相结合的阈值。考虑到从 GNSS-RTK实测信号无法获取不含噪声的纯净信号，只能选择原始监测信号（包含噪声）与其经CEEMDAN分解得到的IMF分量进行相关系数的计算，因而筛选结果可能存在偏差。此外，有效系数仅适用于筛选高频白噪声分量，无法识别低频噪声分量。鉴于此，本文将相关系数和有效系数相结合，以有效系数判定前几项高频白噪声主导分量，以相关系数判定后几项低频噪声分量。具体方法将在下节仿真信号处理中详述。

2.3 平均周期图法基本原理

为了解 GNSS-RTK监测噪声的时频特性，本文基于平均周期图法对信号进行时频变换，进而获取信号的归一化功率谱密度[17]。功率谱密度函数的表达式为

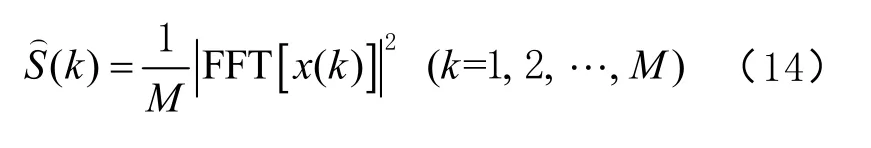
式中：x(k)为监测信号；FFT [x(k)]为x(k)快速傅里叶变换（fast Fourier transform,FFT）结果。

归一化功率谱密度的表达式为

2 仿真信号验证

为了验证本文所提出的、改进CEEMDAN算法联合平均周期图法的有效性，本节通过仿真信号进行验证。利用MATLAB软件，生成一组频率为0.2 Hz的正弦函数信号，其表达式为

再对正弦信号叠加正态高斯白噪声ynoise，构成叠加信号

对信号按照0.1 s间隔进行采样，采样时长为100 s，共计1 000个采样点。正弦信号、噪声信号和叠加信号如图1（a）至图1（c）所示。

运用改进CEEMDAN算法对叠加信号进行分解，并计算了相应的有效系数（R）、IMF分量与正弦信号的相关系数（C1）和 IMF分量与叠加信号的相关系数（C2），结果如表1所示。根据公式（9）计算相关系数阈值，分别为δC1=0.0959和δC2=0.0833 。可以看出，根据IMF分量与叠加分量的相关系数（C2），难以有效筛分白噪声分量；而根据有效系数，可以有效地筛分白噪声分量，其结果与C1判定结果一致，但无法判定低频噪声分量。接下来，基于相关系数和有效系数的单一方法阈值和组合方法阈值筛选 IMF分量，并计算了重构IMF分量与原始正弦函数的相关系数：

1）基于有效系数重构IMF4至IMF9，相关系数为0.972 8；

2）基于相关系数（C2）重构IMF 1至IMF6，相关系数为0.828 3；

3）基于有效系数和相关系数重构 IMF4至IMF6，相关系数为0.975 7。

可以得出，基于相关系数和有效系数相结合阈值的 IMF筛选方法，能够取得最佳效果。此外，根据IMF4至IMF6重构的去噪信号如图1（d）所示，与原始正弦信号（图3（a））呈现了极大的相似性。

3 GNSS-RTK稳定性试验及噪声特性分析

3.1 试验介绍

为了分析环境对 GNSS-RTK监测的影响，进行了不同环境下 GNSS-RTK监测稳定性试验。本次试验选用中海达公司生产的海星达 H32型GNSS-RTK接收机，试验地点位于天津市滨海新区郊外。选择水泥地、亲水平台、草地和变电站等几种环境安置流动站；基准站安置在开阔的水泥地环境下，尽量避免遮挡和强反射造成的多路径效应。接收机采样频率为10 Hz，持续采样3 h。实测信号经过海星达差分软件处理后，电离层误差、对流层误差等与空间相关的误差被大大削弱，残差影响可忽略不计，误差主要来自仪器内部白噪声和不同环境下的多路径效应。首先，对监测点信号进行坐标转换处理；继而，去除平均值，获取GNSS-RTK相对位移时间序列。

图2 GNSS-RTK稳定性试验环境

3.1 数据处理与分析

为了便于计算和展示，截取高程方向时长为1 000 s的序列进行计算。经过改进CEEMDAN分解，得到4种监测环境下的白噪声序列和多路径误差时程序列，并基于平均周期图法计算了 4种环境下多路径误差序列的归一化功率谱密度函数，结果如图3至图6所示。

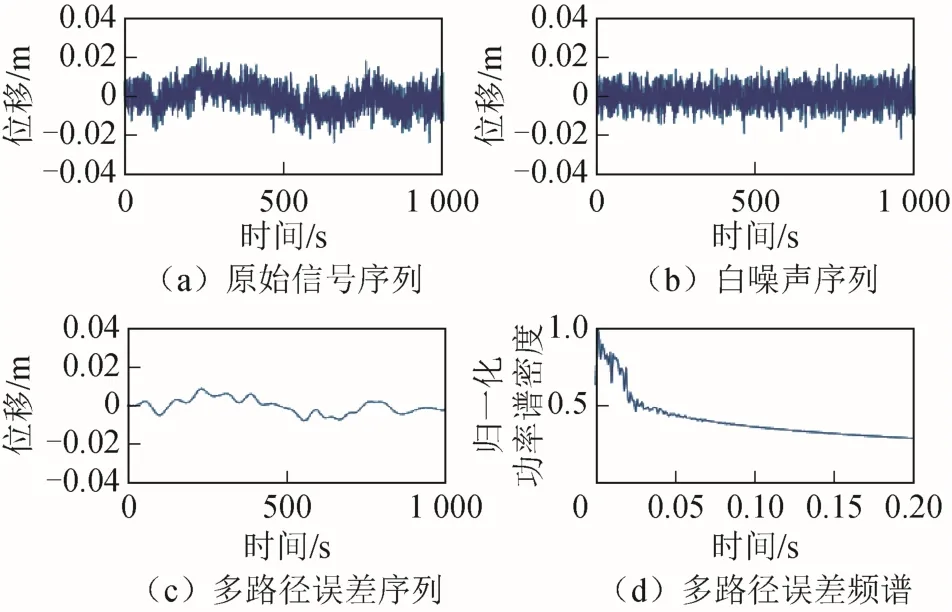
图3 在水泥地环境下，高程方向监测信号时频序列

图4 在水域环境下，高程方向监测信号时频序列

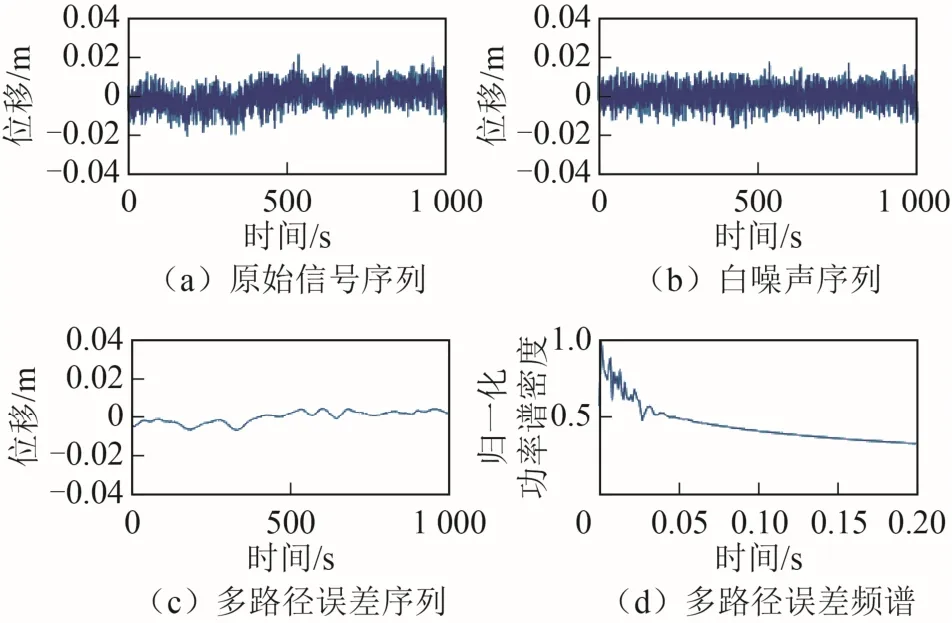
图5 在草地环境下，高程方向监测信号时频序列

图6 在变电站环境下，高程方向监测信号时频序列

除变电站环境外，在水泥地、草地和水域3种环境下，监测信号的位移幅值主要分布在± 0.02 m范围内，监测精度与仪器本身标定精度一致，证明了 GNSS-RTK监测的可靠性。然而，在变电站环境下，监测信号的位移出现较大波动，幅值分布在± 0.04 m范围内。这是由于在变电站环境下，监测信号受到草地、高压电、高压线塔等多重环境因素的干扰，导致监测噪声较大。通过归一化功率谱密度-频率曲线可知，水泥地、草地和水域3种环境下多路径误差主要分布在0.05 Hz范围内，在变电站环境下，多路径误差频谱主要分布在 0.1 Hz范围内。总的来说，多路径误差的频域分布较小，在实际的结构工程监测中，可通过高通滤波器予以滤除。此外，为了避免监测信号淹没在噪声中，采用H32型GNSS-RTK接收机进行监测时，结构的动态变形位移幅值应保证大于0.02 m。

4 结束语

本文研究了环境对 GNSS-RTK监测精度的影响，在4种环境（水泥地，水域，草地，高压电）下，进行了 GNSS-RTK稳定性试验，提出利用改进CEEMDAN算法联合平均周期图法对监测噪声进行分析，得出如下结论：

1）通过采用MATLAB构造仿真信号，证实了改进CEEMDAN算法能够有效提取白噪声。基于相关系数和有效系数相结合的阈值方法，能够筛分IMF分量，其精度高于应用单一方法。

2）通过对4种环境下的实测信号进行时频分析得出：在一般环境下，GNSS-RTK监测位移幅值在± 0.02 m范围内，其精度与仪器标定精度一致，证明了GNSS-RTK监测的可靠性；然而，在草地、高压电、高压线塔等多重因素干扰下，GNSS-RTK监测噪声较大。此外，多路径误差的频域分布较小，主要分布在0.05 Hz范围内，因而可通过高通滤波器予以滤除。