BDS卫星钟时频特性分析研究

张健铤，张晓博，董 哲，李忠华

（1.北京卫星导航中心，北京 100094；2.中国科学院精密测量科学与技术创新研究院 大地测量与地球动力学国家重点实验室，武汉 430071）

0 引言

基于国家安全和经济社会发展需要，我国自主独立建设了北斗卫星导航系统（BeiDou navigation satellite system, BDS），BDS也是继全球定位系统（global positioning system, GPS）、格洛纳斯卫星导航系统（global navigation satellite system,GLONASS）之后的第三个成熟的卫星导航系统[1]。BDS包含地球静止轨道（geostationary Earth orbit,GEO）、倾斜轨道（inclined geosynchronous orbit, IGSO）和中圆地球轨道（medium Earth orbit,MEO）三种不同轨道的卫星。BDS搭载了我国自主研发的高精度小型原子钟，其中北斗卫星导航（区域）系统即北斗二号（BeiDou navigationsatellite (regional) system, BDS-2）搭载的卫星钟，均为国产铷原子钟，北斗三号全球卫星导航系统（BeiDou-3 navigation satellite system, BDS-3）搭载的卫星钟，为国产铷原子钟和国产新型氢原子钟。由于卫星所处的高度、运动状态以及环境存在差异，使得不同轨道的卫星钟性能表现出不同的变化特征[2]。与卫星广播星历相比，高精度的精密卫星钟钟差，更能满足在轨卫星钟钟差特性分析的需要。因此，为了改善BDS的服务能力，有必要根据 BDS的卫星轨道特征和原子钟的物理特性，对BDS卫星钟钟差的特性进行分析[1]。

卫星钟差与轨道密切相关，卫星钟差会吸收轨道径向的误差，因此卫星钟差数据中会呈现出一定的周期特性[3-4]。诸多学者对BDS卫星钟差的周期特性进行了深入研究，如文献[5]研究了 BDS GEO卫星钟差的周期特性，发现其周期分别为24、12、8、6 h；文献[6]基于近一年的钟差数据，全面分析了BDS卫星钟差数据的周期特性，发现BDS GEO卫星钟差的三个主周期依次为12、24和8 h，IGSO卫星钟差的三个主周期依次为24、12和8 h，MEO卫星钟差的三个主周期依次为 12.91、6.44和24 h；文献[7]也指出，卫星钟差存在显著周期项，主要周期分别近似为轨道周期的1/2倍、1倍或2倍。这些研究都充分证明了BDS卫星钟差中显著存在周期项，本文利用标准时频理论，分析了BDS卫星钟周期项的时频特性，并利用具有良好鲁棒性的无为方法[4]，对BDS卫星钟差中显著存在的24 h周期项进行了提取，发现其幅值存在显著变化。

1 BDS星载原子钟

高准确度、高稳定度的原子频标是时间系统的核心，也是确保高精度导航定位的关键。原子频标作为卫星导航系统有效载荷的核心部分，其性能直接决定着导航定位的精度和时频传递的精度[8]。因此，有必要对星载原子钟的在轨性能特征进行分析研究，从而为定位、导航、授时（positioning,navigation and time, PNT）服务提供保障。

截至2018年年底，BDS-3基本系统建成并提供全球服务，在轨工作卫星已达33颗，其中包含15颗BDS-2卫星和18颗BDS-3卫星，具体为5颗地球静止轨道卫星、7颗倾斜地球同步轨道卫星和21颗中圆地球轨道卫星。至2020年6月23号，BDS已经发射完55颗导航卫星，BDS导航卫星发射全部完成，BDS卫星钟在轨情况如表1所示。

表1 BDS卫星钟在轨情况[9]

2 时频分析方法

2.1 标准时频变换理论

标准时频变换（normal time-frequency transform,NTFT）理论，自2007年提出以来，在地球自转参数、卫星钟差等方面得到了广泛的应用[10-14]。

对于函数f(t)，其时频变换为

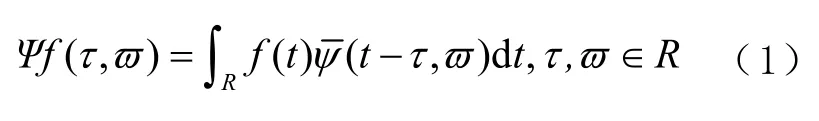
式中：τ和ϖ分别为时间因子和频率因子，线‘-’表示共轭，R为实数域，“||”为取模。

如果式（1）中变换核ψ(t,)ϖ的傅里叶变换

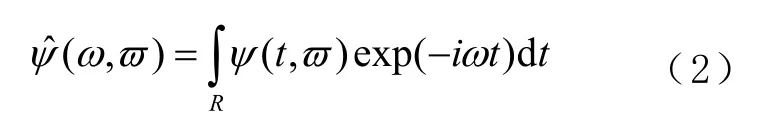
满足：

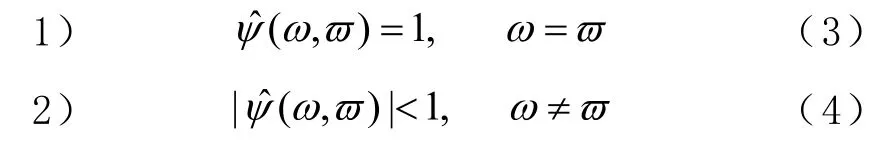
则称式（1）为标准时频变换。

典型的NTFT核函数通常可以表示为

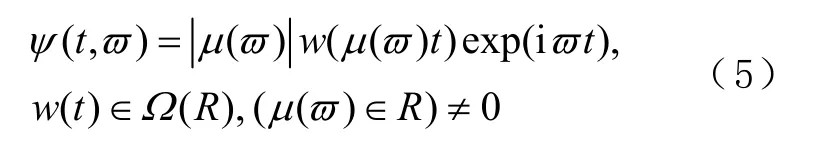
式中，i为虚数符号；Ω(R)为标准窗w(t)的函数空间；尺度因子μ(ϖ)为任何情况下都不一直为0的函数，比如为：ϖ,ϖ2/3,ϖ5等。若μ(ϖ)=1，则式（2）为相位无偏的加博尔（Gabor）变换（Gabor transform, GT），若μ(ϖ)=ϖ，则式（2）为标准的小波变换（normal wavelet transform, NWT），即

在式（5）和式（6）中，若窗函数的傅里叶变换满足式（7）的条件，则该窗函数为标准窗。式（7）的表达式为

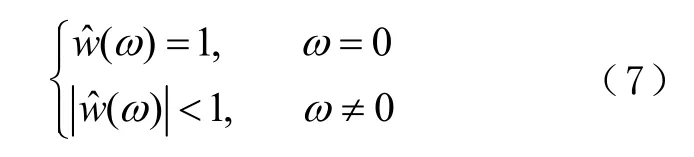
窗函数w(t)通常选择标准的高斯窗，其表达式为

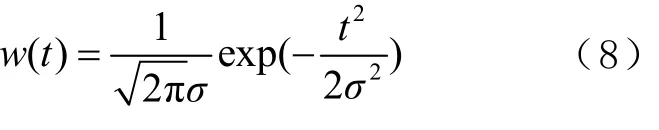
式（8）中的σ＞0，因子σ的设置至关重要，该参数直接影响NTFT的时频分辨率。

2.2 无为方法

为了从标准时频谱上简洁、高精度地获取调和函数和时变调和函数，文献[11, 14]提出了无为方法，该方法本质是一种线通滤波器，是一种对调和函数和时变调和函数的估计。

无为方法的准则如下：调和函数h(t)表达式为

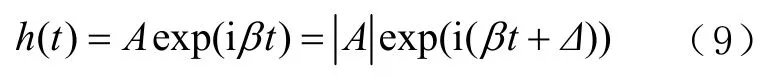
将式（7）代入标准时频变换，即可得到

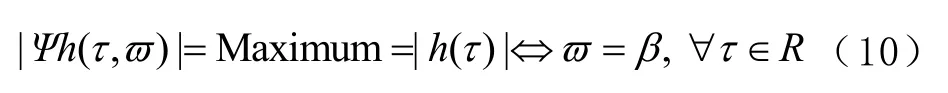
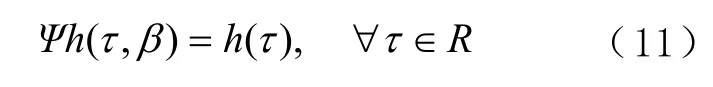
式中：A为复数幅值；常数β为角频率；Δ∈ [ 0,2π)为初始相位；(βt+Δ)为瞬时相位；∀为“任何情况下”，“⇔”为“当且仅当”。

3 BDS卫星钟时频分析结果

3.1 数据来源

本文数据采用的来源于武汉大学卫星导航定位技术研究中心[9]发布的间隔 30 s，从 2020年 3月1日至2020年5月23日一共84 d的BDS-2卫星钟差数据数据，为了更好的分析BDS卫星钟周期项的时频特性，本文选取其中没有明显异常的49天数据作为分析对象。

3.2 时频分析结果

针对BDS卫星钟差数据，首先利用高次多项式（文中采用四次多项式）消除趋势项，然后利用NTFT得到标准时频谱，如图1所示。

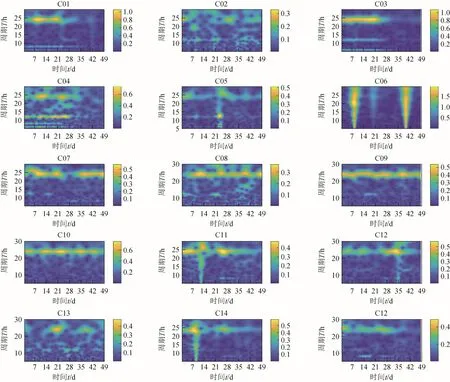
图1 BDS-2卫星钟的时频

本文分析了正在运行的、在轨的 C01至 C14及C16号卫星的钟差，从图1中可以看出，除C06号卫星受异常值干扰外，其它BDS卫星钟都存在显著的24 h周期项，部分卫星钟存在12、8、6 h周期项（如C04号卫星）。

由于24 h周期项普遍存在BDS卫星钟差中，本文采用无为方法对其进行提取，得到选取 BDS卫星钟差的24 h周期项，如图2所示。

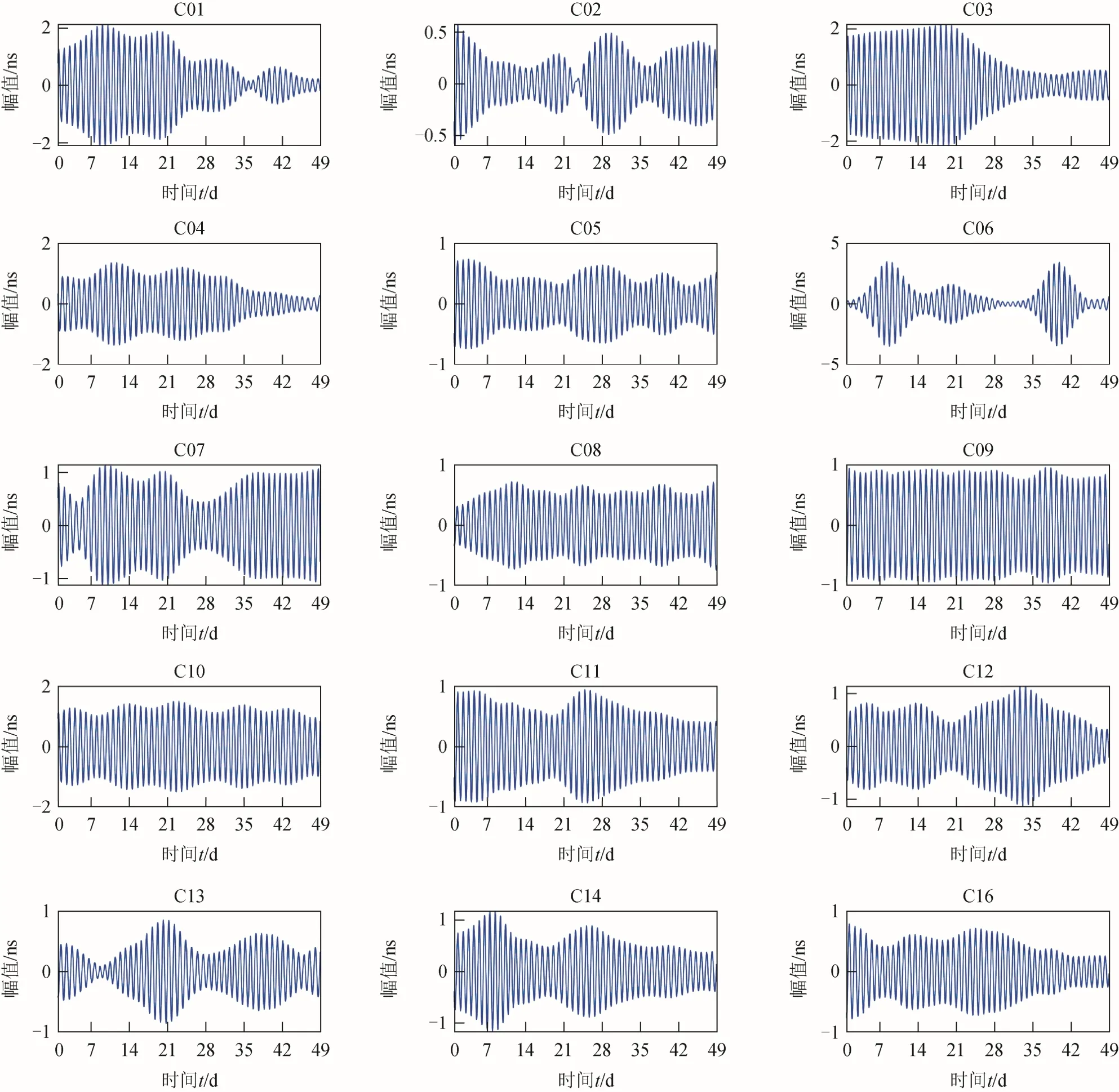
图2 BDS卫星钟的24 h周期项

从图2中可以看出，BDS卫星钟的24 h周期项，幅值最大为2 ns（如C01、C03号卫星），普遍为1 ns，最小为0.5 ns（如C02号卫星），C06号卫星由于受异常值影响较大，因此幅值大于2 ns的部分为不可信部分。另外，从图2还可以看出，BDS卫星钟的24 h周期项幅值存在显著变化。

4 结束语

本文利用标准时频变换理论对选取的BDS-2卫星钟的时频特性进行了分析，并对显著存在的24 h周期项进行了有效提取，得到如下结论：

1）BDS卫星钟都显著存在24h周期项，部分卫星钟还存在12、8、6 h周期项；

2）BDS卫星钟的24 h周期项幅值普遍在1 ns左右，最大值为2 ns，最小值为0.5 ns；

3）BDS卫星钟的 24 h周期项幅值存在显著变化。

随着BDS-3卫星钟开始启用，其时频特性需要进一步分析，对于BDS卫星钟差周期项幅值出 现幅值变化的原因还需要进一步研究。