基于信道状态信息的非接触式人员动作识别方法

郝占军，张岱阳，党小超，段 渝

（1.西北师范大学 计算机科学与工程学院，兰州 730070；2.甘肃省物联网工程研究中心，兰州 730070）

0 概述

动作识别是当前的热门研究方向之一，具有广阔的应用前景［1］。传统的动作识别技术基于传感器以及摄像头等设备，如文献［2］利用视频中提取的信息来识别人体行为动作。虽然利用摄像头识别动作的精度较高，但是摄像头在无光或弱光环境下无法有效工作，且存在拍摄盲区等问题。基于传感器的动作识别技术应用范围广泛，技术较成熟，如文献［3］利用传感器进行医疗动作识别，但多数传感器需要进行穿戴，且传感器的部署和维护成本较高。利用Wi-Fi 信号进行动作识别能够有效克服上述两种方法的缺陷。首先随着Wi-Fi设备的大量部署，Wi-Fi 的普适性大幅增强，其次利用Wi-Fi 信号进行的动作识别属于非侵入式检测，较好地保护了用户的隐私。到目前为止，很多相关研究都是以Wi-Fi 信号为基础的，如文献［4-5］利用Wi-Fi 信号进行室内人员的定位，文献［6］利用Wi-Fi 信号检测人员的日常行为。

在基于Wi-Fi 信号的相关研究中，主要是利用从Wi-Fi 设备通信协议中媒介控制层提取的接收信号强度（Received Signal Strength，RSS）来进行研究，如文献［7］使用RSS 信息进行室内人员活动识别，但是由于RSS 受多径效应和窄带干扰的影响较大，导致其不稳定，对人体的动作不敏感，最终造成测量精准度不高。相较于RSS，信道状态信息（Channel State Information，CSI）具有更大的优势，CSI 是细粒度的物理信息，并且CSI 受多径效应的影响较小，具有较高的稳定性。很多动作识别方法的设计是基于CSI的，如文献［8］利用CSI 进行穿墙人体动作的检测，文献［9］检测人的驾驶动作，文献［10］使用CSI 进行细粒度的手势识别。

本文提出一种基于CSI 的非接触式人员动作感知方法Wi-Opera。离线阶段采集大量京剧动作数据形成样本集，利用巴特沃斯低通滤波器过滤高频的环境噪声，并运用多贝西小波（Daubechies Wavelets）及符号小波（Symlet Wavelets）对低频部分进行去噪和平滑。通过PCA 算法提取每个动作的特征并为每个京剧动作建立各自的决策树，将所有决策树集成为随机森林模型，并对其进行训练。在线阶段采集动作的原始CSI 信号，经过相同处理后输入随机森林进行分类识别，匹配每一棵决策树，最终以多投票机制输出识别结果。

1 相关理论

1.1 信道状态信息

信道状态信息（CSI）描述无线通信链路的信道特性。多路径场景下的信道频响R(f)表示为：

其中，K为多路径的总数，αl为第l条链路的振幅信息，θl表示第l条链路的相位信息，δ(∂)表示一个脉冲函数。根据正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术，路由器采用相互正交的多载波传递信息［11］，可以从Wi-Fi 信道中提取到CSI 信息，在信道带宽为40 MHz 时每组CSI 都含有114 个子载波的相位和振幅信息，其第k个子载波函数表示为：

其中，|fk|为第k个子载波的振幅值，j sinθk为相位值，相较于相位信息，振幅更加稳定。因此，本文采用振幅信息作为特征值进行研究。

1.2 巴特沃斯低通滤波器

巴特沃斯低通滤波器是电子滤波器的一种［12］，目的是过滤由环境引起的高频噪声并保留由人体动作引起的低频段CSI 信号，其幅度平方函数为：

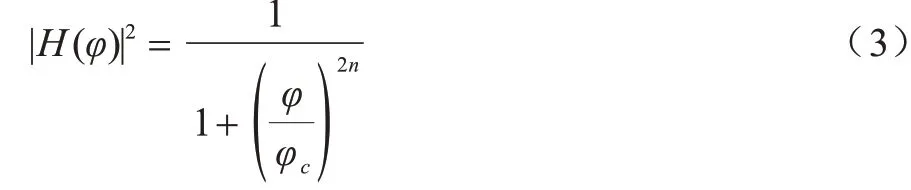
其中，n为滤波器的阶数，φc为截止频率。过滤后的CSI 动作数据去除了高频的环境噪声，使低频部分的动作信息得到保留。

1.3 小波变换

由于小波变换具有多分辨率以及时频局部化方面的良好表现［13］，本文利用多贝西小波与符号小波对数据进行处理。多贝西小波也称为db 小波［14］，其主要特性是能突出信号在某一方面的特征。小波函数的计算公式如下：

其中，a为小波函数的尺度，τ为平移量。Symlet小波是对db 小波的一种改进［15］，简称sym 小波。Symlet 小波具有更好的对称性，因此能减少小波变换对CSI 信息进行拆分处理和重新构组时的失真率。利用多贝西小波可以处理CSI 信息低频部分，使其特征更加突出。然后使用Symlet小波处理，可以使CSI数据更加平滑。通过实验得出利用多贝西3 号小波（下文称db3 小波）进行5层分解后再利用Symlet8号小波（下文称sym8小波）分解8 层，处理后的数据效果最好。

1.4 PCA 降维

PCA 算法是利用数学降维的方法找出一个或几个综合变量代替原来众多的变量，使这些综合变量尽可能多地反映原来变量的信息量［16］。在高维的空间中寻找一个低维的正交坐标系，通过推导和投影，将高维的数据转化为低维数据。PCA 算法的步骤为首先进行去中心化，求出每个特征的均值，再用每个特征的数据减去均值，然后计算协方差矩阵，其计算公式为：

其中，m为元素个数，piqi为矩阵中的元素位置。计算协方差矩阵的特征值以及特征向量，再将特征值从大到小进行排列，最后选取最大的特征。

2 Wi-Opera 方法

2.1 Wi-Opera 方法介绍

本文以京剧动作为对象进行研究。首先离线阶段采集每个京剧动作的CSI 信息，并且把振幅作为每个动作的描述，将采集的CSI 原始信号进行预处理并用PCA 算法提取每个动作的特征值，利用提取的特征值为每个京剧动作建立各自的决策树，将所有动作的决策树集成为随机森林模型并用样本集进行训练。在线阶段，采集实验人员在不同的实验环境中做出的动作数据并对所有数据进行预处理，最后将数据输入随机森林模型中识别出具体的京剧动作。图1 所示为Wi-Opera 的流程。

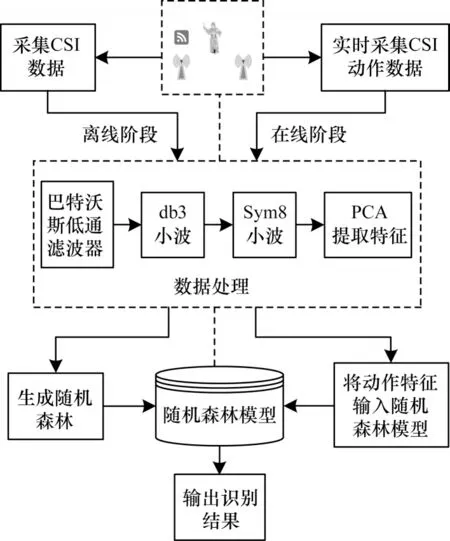
图1 Wi-Opera 方法流程Fig.1 Procedure of Wi-Opera method

2.2 数据获取

本文共选取了6 个京剧动作，分别为生角、刀马旦、青衣、老旦、净角、丑角。通过支持IEEE 820.11N协议且搭载了Atheros AR9580 无线网卡的商用路由器采集CSI 京剧动作信号。实验设置了2 根发射天线、3 根接收天线和6 条数据链路。

由于身体不同部位对信号的折射、反射和散射，导致每个动作对6 条链路的影响是不同的。但是由于每个动作都是站立动作，因此不同动作的区分主要是手臂以及腿部的位置。躯干部位的振幅对不同动作的区别度并不是很大，如果将6 条链路的数据全部进行训练会导致数据过于复杂，过于冗余的数据会使计算量上升从而使性能下降。

如何将一个动作中产生影响最显著的链路提取出来是一个需要解决的问题。在上文的研究中发现手臂以及腿部对链路的振幅影响最大，所以选择了能反映这3 个部位的链路作为该动作的特征。

本文对文献［17］提出的链路选取方法进行改进，构建一个适用于本文方法的模型。通过PCA 方法计算每条链路的主要影响因素，然后构造拉格朗日函数［18］并对其求偏导从而为动作的每条链路赋予一个权重，选取权重前三的链路作为该动作的主要特征。

具体操作的伪代码如下：

通过上述的链路选取操作，6 个动作的振幅特征如图2 所示。

图2 对应于不同动作的CSI 振幅特征Fig.2 CSI amplitude characteristics corresponding to different actions

2.3 数据处理

2.3.1 动作数据降噪

由于环境噪声的影响，CSI 振幅数据出现很多毛刺，掩盖了人体动作引起的CSI 信号。为了去除环境噪声，本文采用了Matlab 自带的巴特沃斯低通滤波器。经过实验得出，设置通带频率为50 Hz，阻带频率设置为100 Hz，通频带波动设置为2 dB，阻带衰减设置为3 dB 时滤波器过滤出的数据效果最好。然后将动作CSI 数据输入设计好的滤波器中，最后得出滤波后的数据波形。根据巴特沃斯低通滤波器在通带内频率响应曲线具有最大限度的特性，保证了在滤掉噪声的同时，保留了由动作引起的CSI 振幅真实变化。数据过滤前后的对比如图3 所示，其中，图3（a）方框中为噪声数据波形。从图3 可以看出，过滤后的CSI 信号变得平滑，证明利用该方法可以有效去除高频环境噪声。对于滤除高频噪声的信号，本文利用db3 小波及sym8 小波进行进一步处理。首先将数据输入第一个小波函数中，第一个小波函数的波基函数设置为db3，细节系数为sure，分解层数为8。将经过db3 小波处理后的数据输入第二个小波函数中，第二个小波函数的波基函数设置为sym8，分解层数为5。通过小波函数的处理，进一步去除了噪声，也使动作数据的特征更加明显。

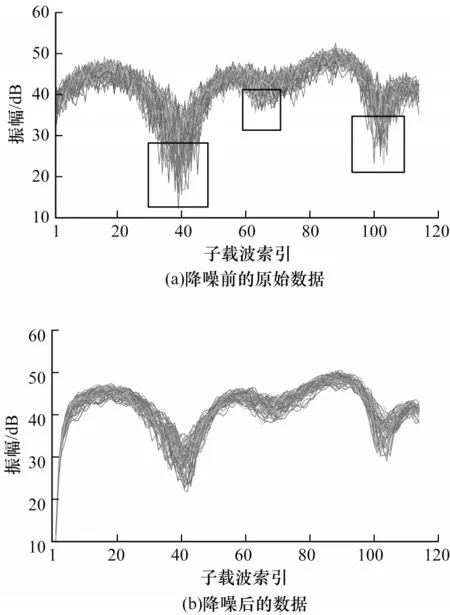
图3 CSI 动作数据的降噪Fig.3 Noise reduction of CSI action data

图4（a）为未经过处理的数据，图4（b）为经过db3 小波以及sym8 小波处理后的数据。从图4 结果可以看出，处理后的数据进一步去除了噪声并且变得更加平滑，有利于下一步的特征提取。

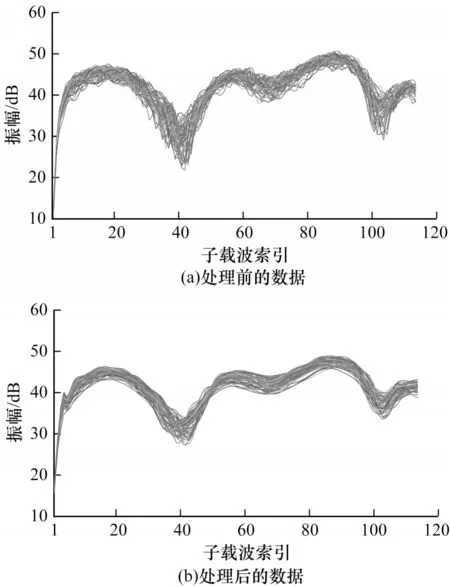
图4 小波变换处理前后数据的对比Fig.4 Comparison of data before and after processing using wavelet transform

2.3.2 特征提取

图5所示为利用PCA算法提取的特征，其中，图5（a）为一个丑角动作所有包的CSI信息，图5（b）为利用PCA算法提取到其中的主成分信息。

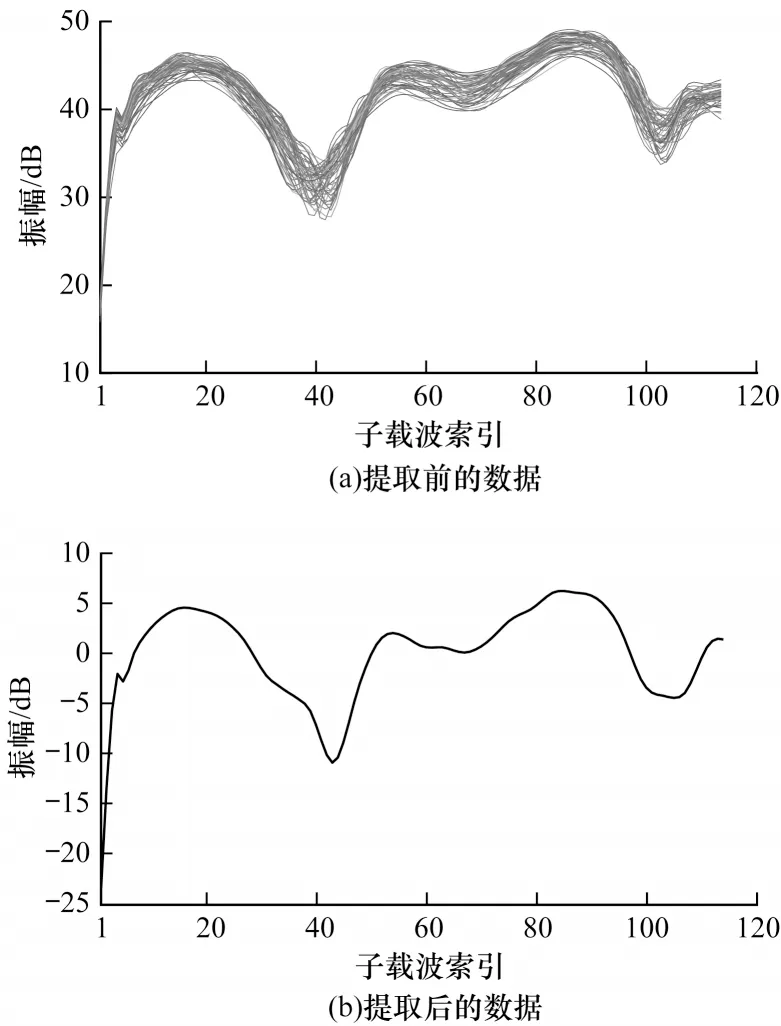
图5 PCA 算法提取的特征Fig.5 Features extracted by PCA algorithm

利用PCA 算法对去噪后的CSI 动作信息降维之后进行主成分的提取。首先将利用小波变换处理后的动作数据输入到主成分分析函数［coeff，score，latent］中。其中，coeff 为各个主成分的系数，score 为各个主成分的得分，latent 为输入动作数据的特征值。计算输入动作数据的特征值贡献率，若累计贡献率到达85%以上，则可以使用此动作数据的特征信息表示该动作大部分信息。将该主成分提取出来作为输入动作数据的主要特征。由于输出的数据只有114 个特征，从而达到了降维的效果。

2.4 离线阶段

2.4.1 决策树

分类和回归树（Classification and Regression Tree，CART）算法是以实例为基础的归纳学习算法，具有易于实现和高效性等优点［19］。本文利用CART算法进行CSI 京剧动作振幅特征的划分，所以只生成分类树。分类树的生成以基尼指数为基础，计算公式为：

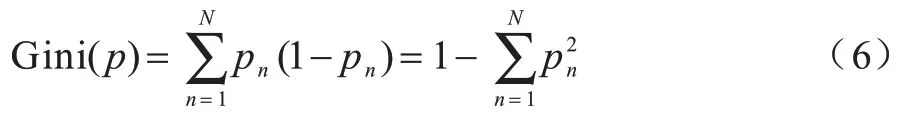
其中，N为样本的个数，pn为样本属于第n类的概率。基尼指数的意义是用来表示不确定性，所以对于一个给定的样本集M，其基尼指数为：

其中，Cn为第n个样本值。此时对于该样本集M，根据其特征A是否取某个值a可以将M分为M1和M2两个部分。在A的条件下，M的基尼指数表达式为：

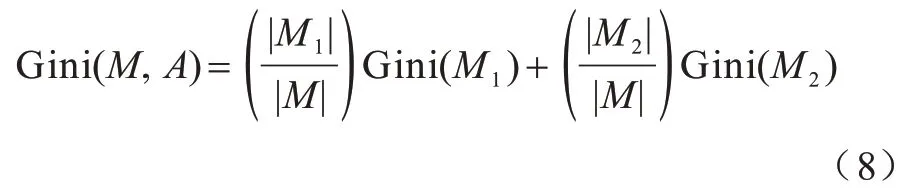
其中，Gini(M,A)表示特征A在取a值分割样本集M后的不确定性，相当于根据A划分的两个集合分别求基尼指数，然后根据经验概率期望得到特征A下的M的基尼指数。Gini(M,A)越大，不确定性越高。

决策树生成的具体步骤如下：

步骤1采集大量京剧动作数据，进行去噪后利用PCA 算法提取其每个动作振幅的特征值。每个动作数据的特征值构成一个样本集，最后生成6 个样本集。

步骤2对每个京剧动作的样本随机有放回地抽取其中的2/3 作为每个动作的训练集。

步骤3对于一个动作的样本值，选取其所有的振幅特征值，然后根据式（6）～式（8）计算其基尼指数。

步骤4选择基尼指数最小的特征及其对应可能的划分点作为最优特征与最优划分点，从结点分裂两个子结点，将样本集中的数据分配到两个子结点中。

步骤5递归调用步骤3、步骤4，直到样本集的基尼指数小于设定的阈值、结点中的样本数小于设定的阈值或特征值全部用完时停止建树。

步骤6生成完整的决策树。

2.4.2 随机森林

随机森林是以多棵决策树为基本分类器，通过集成学习后得到的一个组合分类器，也是一种非参数集成方法［20］。将6 个京剧动作的决策树集成为随机森林模型，如图6 所示，其中，●为动作特征。

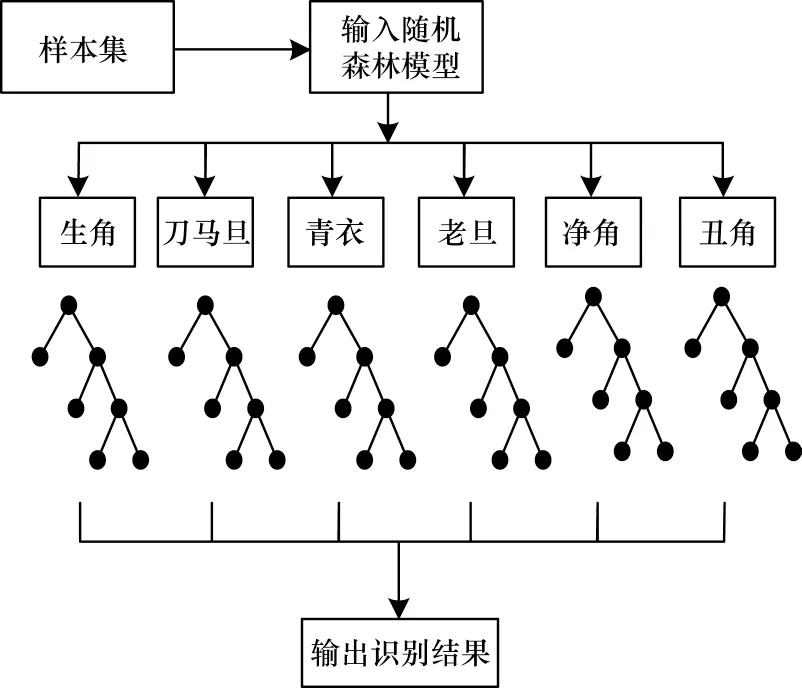
图6 随机森林模型Fig.6 Random forest model

由于决策树建立的随机性，因此不需要进行剪枝处理，每棵决策树完全生长，最后利用多投票机制得出分类识别结果。样本抽取和决策树建立的随机性，使得随机森林算法针对样本不均衡的问题得到了很好的解决，并且也解决了决策树过拟合的问题。同时，随机森林的学习过程较快，易于实现并行化，节约了运行时间。

2.5 在线阶段

在线阶段利用设备采集到京剧动作原始的CSI振幅信息，经过去噪和特征提取后取得动作的振幅特征值。将振幅特征值输入随机森林模型中进行识别，最后模型输出识别结果，具体步骤如下：

步骤1实时采集实验人员的京剧动作CSI 振幅数据。

步骤2将实时采集到的动作振幅数据进行去噪及平滑处理。

步骤3利用PCA 算法提取该动作数据的主要振幅特征。

步骤4将该动作的振幅特征值输入到随机森林模型中，并行遍历其中所有的决策树，每个决策树都输出一个分类结果。

步骤5将每棵决策树的结果进行汇总，在所得到的结果中，利用投票机制得到该动作的分类结果。

3 实验验证

3.1 实验配置

本文实验采用两台装载Atheros AR9580 网卡芯片的TP-Link WDR4310 路由器以及两台Dell Alienware m15 笔记本电脑。

两台路由器通过使用OpenWrt 修改其内核，可以利用CSI Tool［21］将Wi-Fi 信号中的CSI 信息提取出来。两台笔记本电脑都装有Xshell6 以及Winscp，并分别与两台路由器相连，一台连接发射端（Rx），另一台连接接收端（Tx），其作用为路由器内核OS 的操作入口。通过发射端电脑建立热点构建局域网，接收端电脑接入局域网的方式使两台设备建立连接。通过Xshell6 可以让电脑连接到路由器并控制发射端和接收端路由器分别进行发包和收包的操作。之后接收端电脑通过Winscp 将动作数据从路由器中提取出来，以进行下一步数据预处理操作。

为研究不同实验环境对Wi-Opera 方法的影响，实验环境选择了空旷的实验室、办公室以及走廊。图7 为3 个实验环境图，图8 为实验环境平面结构。

图7 3 种实验环境图Fig.7 Three experimental environment diagrams

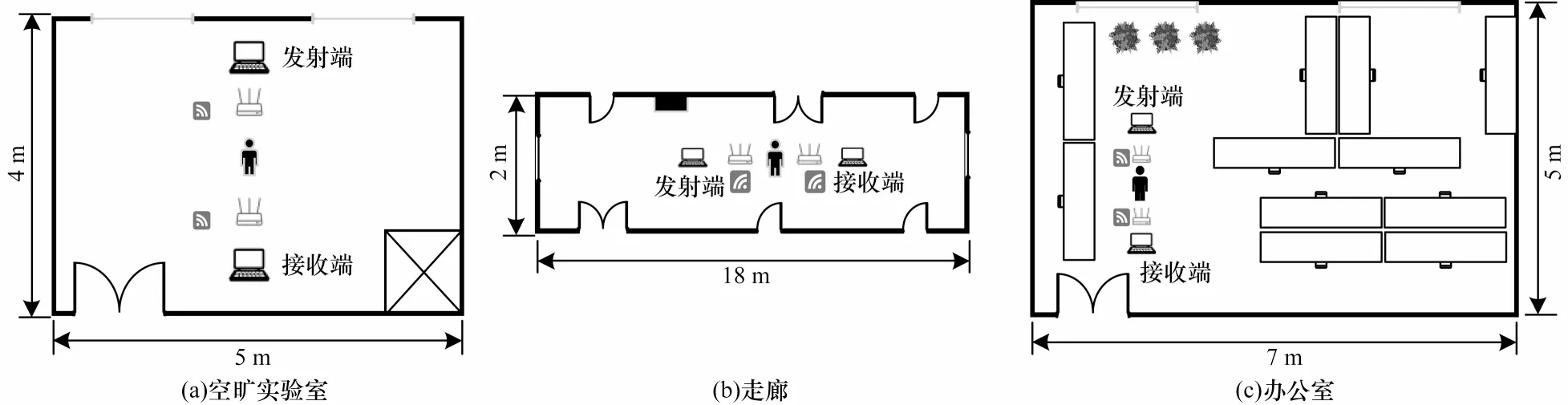
图8 实验环境平面结构Fig.8 Plan structure of experiment environment

3.2 实验设计

本文共进行4 组对比实验，分别是：发射端与接收端间距对动作识别结果的影响；不同实验环境对识别结果的影响；不同频段对识别结果的影响，用户多样性对识别结果的影响。为了获得较大的信噪比以提高CSI 信号对人体动作的灵敏度，本文实验将发包速率设置为10 包/s。实验选取4 名实验人员在发射端与接收端之间做不同或相同的京剧动作。

1）离线阶段。分别采集6 个京剧动作的数据，每个动作数据采集1 000 个样本构成样本集，经过Wi-Opera 方法的处理，构建随机森林模型并对其进行训练。表1 为4 名实验人员的具体数据。

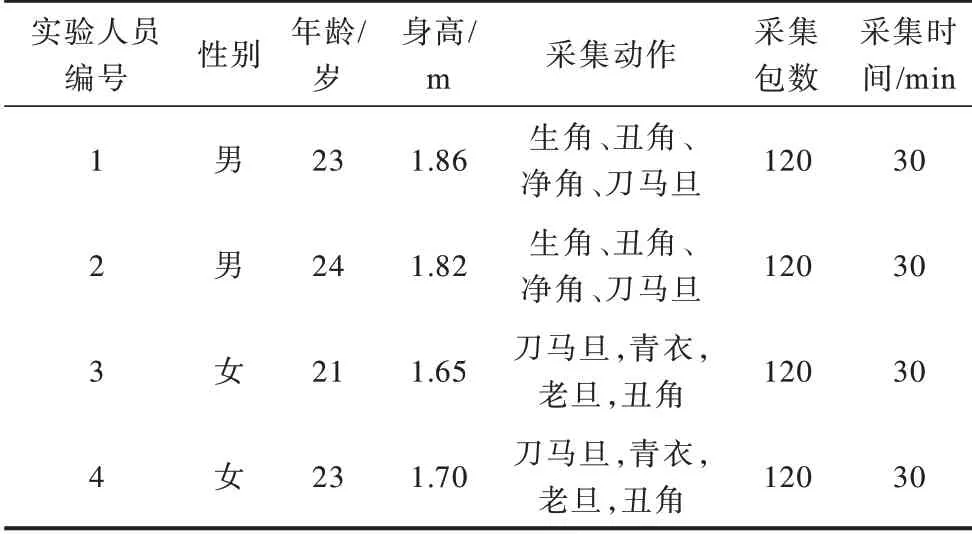
表1 实验人员参数Table 1 Experimenter parameters

2）在线阶段。在3 个实验环境中，实验人员在发射端和接收端中间做出京剧动作，接收端电脑实时采集该动作的CSI 数据并保存。使用Wi-Opera 方法对实时采集的动作数据进行处理，再将处理过的数据输入随机森林模型，最终输出识别结果。

3.3 实验验证

3.3.1 发射端与接收端间距对识别结果的影响

发射端与接收端不同的间距也会对识别结果产生影响。为找到识别效果最好的距离，本文在3 种环境中各做了9 组实验。在其他变量不变的情况下，改变发射端与接收端的间距进行实验，实验间距分别为1.1 m、1.2 m，1.3 m、1.4 m、1.5 m、1.6 m、1.7 m、1.8 m、1.9 m。将这9 组实验采集到的数据经过Wi-Opera 方法处理后，输入随机森林模型进行识别。3 种环境的识别结果如图9 所示。

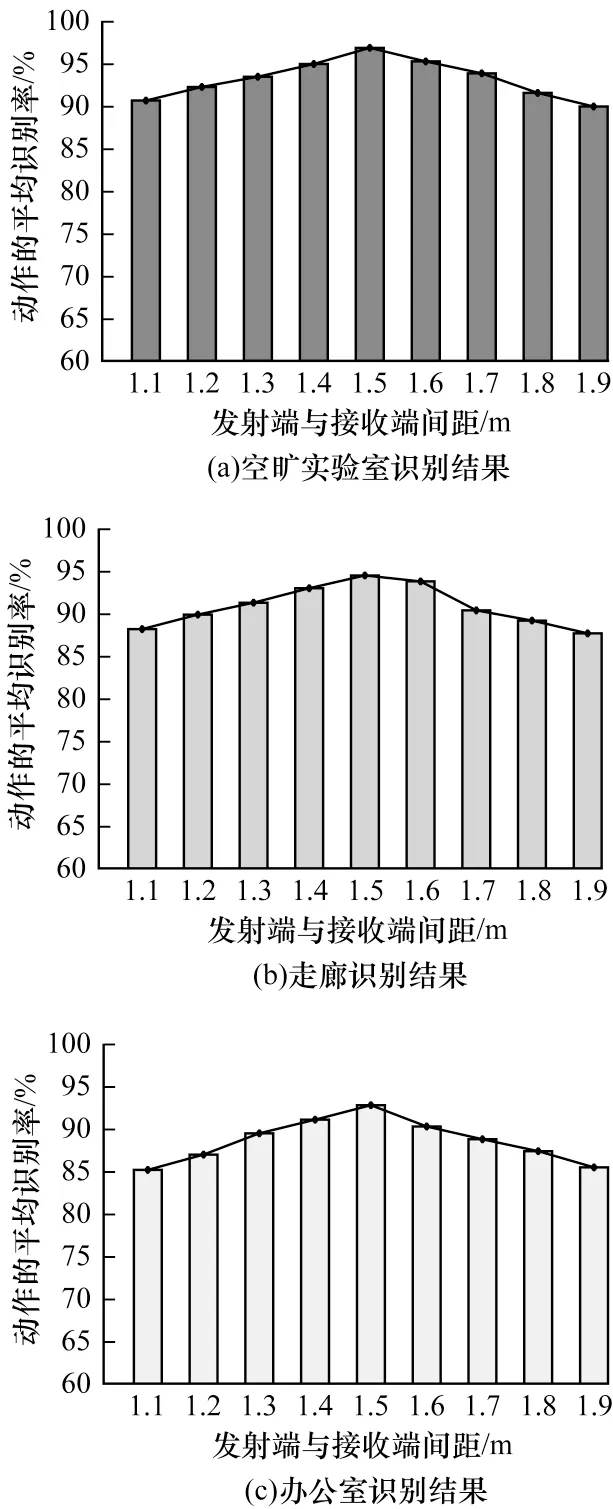
图9 3 种环境下不同间距的识别结果Fig.9 Recognition results of different spacing under three environments

从图9 可以看出，在3 种环境下发射端与接收端的间距在1.1 m～1.5 m 时识别结果逐步上升，间距在1.5 m～1.9 m 时识别结果逐步下降，在1.5 m 时识别结果达到最佳。因此得出发射端与接收端的间距在1.5 m 时为最佳实验距离。

3.3.2 不同实验环境对识别结果的影响

为验证多径效应对实验结果的影响，本文分别在3 个不同的实验环境下采集数据，并且考虑到在同一环境中，图10 所示的LOS（Line Of Sight）场景与NLOS（Non Line Of Sight）场景也会对实验结果造成影响，因此也测试了在3 个不同环境下LOS 与NLOS 的影响。

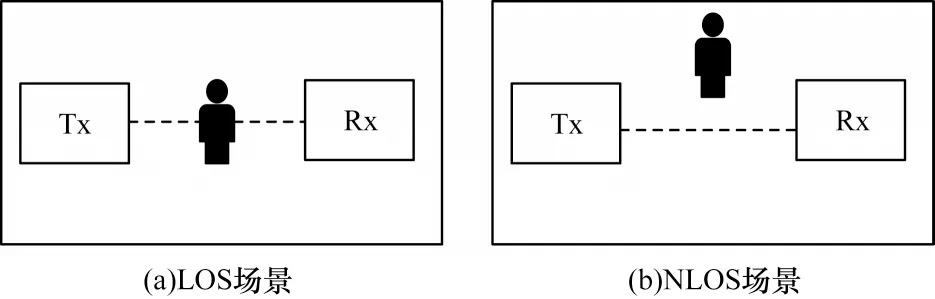
图10 LOS 场景与NLOS 场景Fig.10 LOS and NLOS scenarios

3 个实验环境的多径效应从高到低排列依次为办公室、走廊和空旷实验室。将发射端与接收端的间距设为1.5 m，3 个环境的动作识别结果如图11 所示。

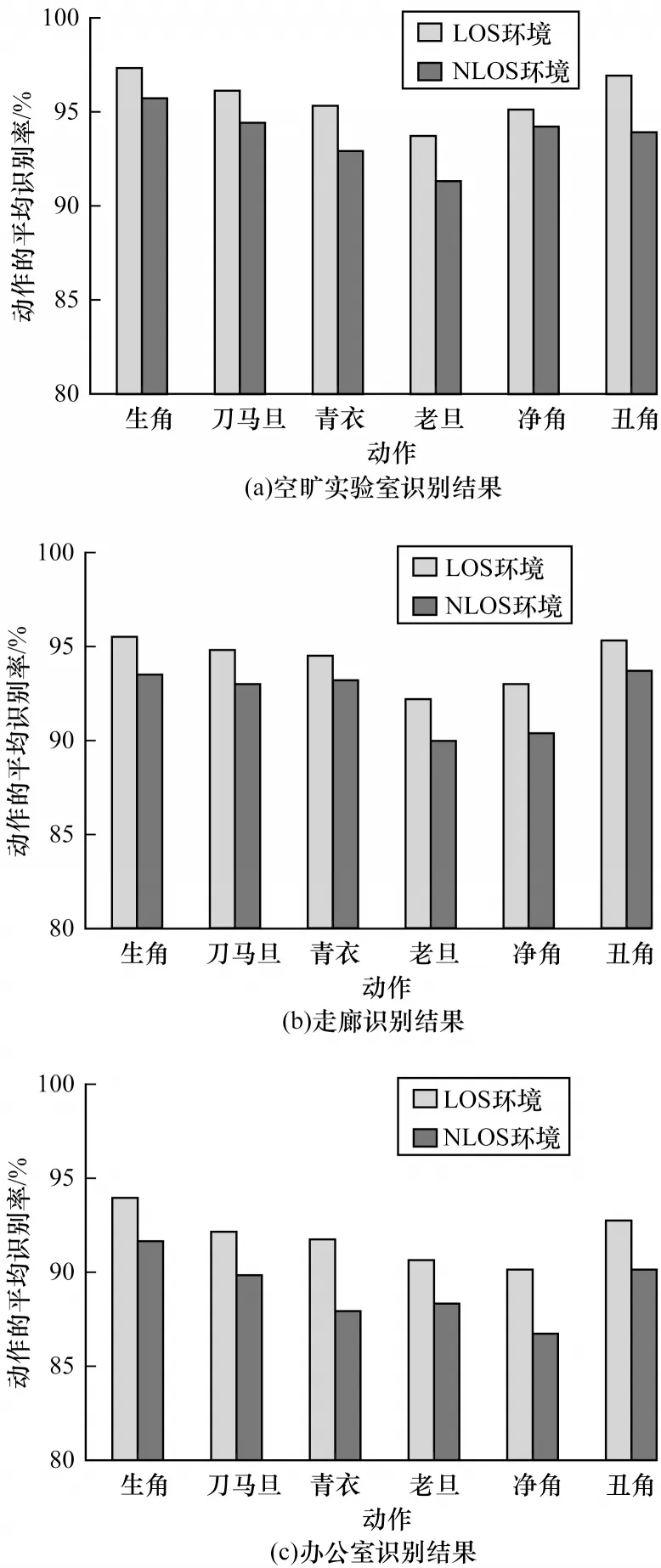
图11 3 种环境下LOS 与NLOS 的识别结果Fig.11 Recognition results of LOS and NLOS under three environments

从实验结果可以看出，空旷实验室环境的识别结果最高，办公室环境的识别结果最低，表明在受多径效应影响小的环境中实验效果好。此外，在LOS环境下的实验结果比NLOS 环境下要更好。

3.3.3 用户多样性的影响

本文选取了两男两女共4 名实验人员。在空旷教室环境下，让4 名实验人员做同一京剧动作，以此来验证用户多样性对Wi-Opera 方法的影响。将发射端与接收端距离设置为1.5 m，4 名实验人员分别在发射端与接收端中间做丑角动作，4 名实验人员的丑角动作CSI 振幅数据如图12所示。

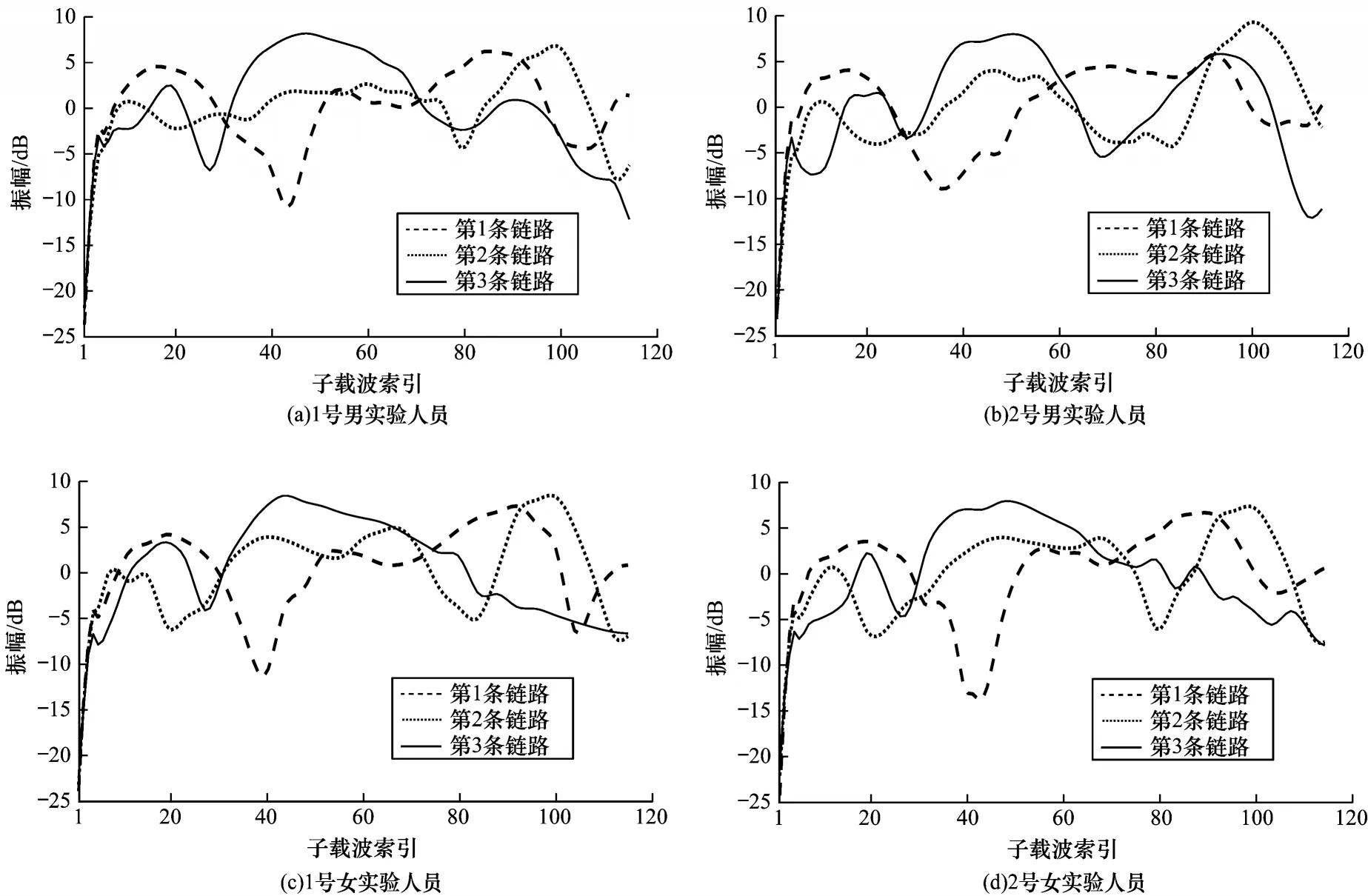
图12 4 名实验者丑角动作的振幅特征图Fig.12 Amplitude characteristic diagram of four experimenters Harlequin action

从图12 可以看出，由于每个人的体型和动作幅度有所差异，4 名实验者的动作CSI 振幅也存在较少差异，但总体动作变化趋势基本一致。以上结果表明Wi-Opera 方法具有较强的鲁棒性。

3.3.4 不同频段对识别结果的影响

本文选择在40 MHz 带宽和5 GHz 的频段下进行实验，其原因为相较于20 MHz 带宽和2.4 GHz 频段，5 GHz 频段具有更强的抗干扰性，能提供更加稳定的信号。为验证5 GHz 频段的识别结果高于2.4 GHz 频段，分别在5 GHz 频段与2.4 GHz 频段下采集相同人员的6 个动作数据。由于2.4 GHz 频段下共有56 条子载波，而在5 GHz 频段下有114 条子载波，因此用前文中同样的方法训练了一个适用于2.4 GHz 频段下的随机森林模型。在3 种环境下，分别在5 GHz 频段和2.4 GHz 频段下采集同一实验人员的全部动作数据，将实验数据分别输入两个随机森林模型进行识别，其综合识别结果如图13 所示。

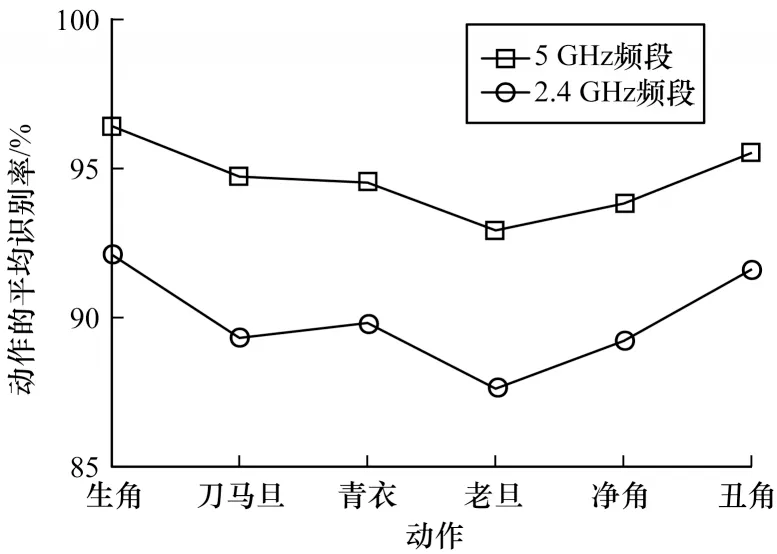
图13 不同频段识别结果对比Fig.13 Comparison of different frequency bands identification results

从图13 可以看出，在3 种环境下，2.4 GHz 频段下的平均识别结果为89.9%，5 GHz 频段下的平均识别结果为94.6%。实验结果表明，本文方法中5 GHz频段下的识别结果高于2.4 GHz 频段下的识别结果。

3.3.5 动作规范性对实验结果的影响

动作的规范与否也会对实验结果造成影响，所以本文研究了动作规范性对实验结果的影响。不规范动作的定义是身体大体的趋势跟规范动作相似，只是动作的幅度和手臂及腿部的位置跟规范动作有很大的区别。因此，采集所有的动作振幅数据并用Wi-Opera 方法进行处理和识别。规范动作与不规范动作的综合识别结果如图14 所示。

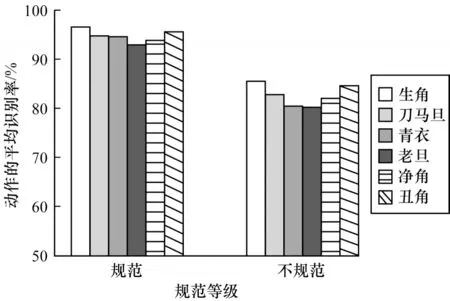
图14 不同规范等级识别结果对比Fig.14 Comparison of recognition results of different specification levels

从图14可以看出，动作的规范程度会对识别精度造成影响。当动作不规范时，识别的结果也会相应下降。当动作规范时综合识别结果为94.6%，但是当动作的规范等级为不规范时，综合识别结果仍有82.3%。实验结果表明，Wi-Opera方法具有较强的鲁棒性。

4 实验结果与分析

本文选取了4 名实验者分别做6 个动作进行测试，其综合实验结果如图15 的混淆矩阵所示。

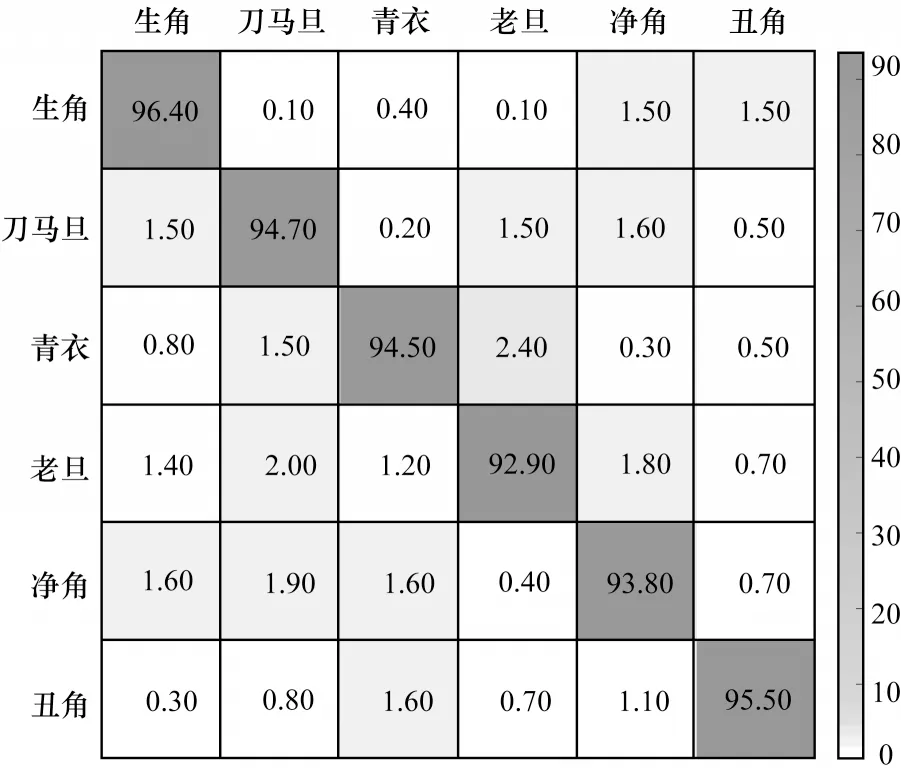
图15 综合混淆矩阵Fig.15 Comprehensive confusion matrix

从混淆矩阵的结果可以得出，Wi-Opera 方法的综合识别结果为94.6%。每个动作的综合识别结果均在90%以上，证明Wi-Opera 方法能很好地区别6 个京剧动作并具有较强的鲁棒性。

此外，为验证Wi-Opera 方法具有较好的整体性能，本文还与文献［22-24］中的动作识别方法进行了对比。对比结果如表2 所示。

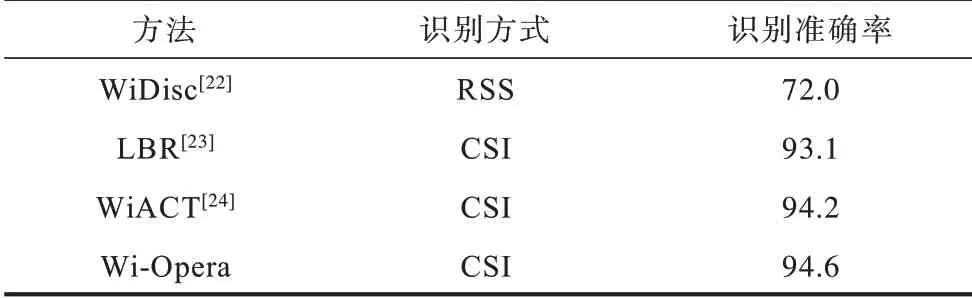
表2 不同方法识别结果比较Table 2 Comparison of recognition results of different methods %

文献［22］运用RSS 信号进行动作的识别，识别结果约为72%。文献［23］提出了一种轻量级的CSI动作识别方法，代表了以一种动作识别方法的体系，识别结果达到了93.1%。文献［24］利用多普勒频移作为特征并使用极限学习机进行动作分类，识别结果达到了94.2%。从表2 结果可以看出，本文利用的CSI 动作识别方法明显优于基于RSS 动作识别的方法。并且对比两种基于CSI 的动作识别方法，本文的识别效果也具有较高的识别结果，证明Wi-Opera方法具有较高的识别精度。

5 结束语

本文提出一种基于信道状态信息的非接触式人员动作感知方法Wi-Opera。离线阶段采集京剧动作数据经过巴特沃斯低通滤波器，通过小波变换对动作信号进行去噪和平滑后再利用PCA 算法降维并提取特征，最终构建每个京剧动作的决策树形成随机森林模型。在线阶段将实时采集的动作振幅数据经过相同方法处理后，输入随机森林模型进行识别，从而输出识别结果。实验结果表明，Wi-Opera 方法具有较好的识别精度和较高的鲁棒性。