光子静质量与库仑定律关系的再论证

何池航 李智华

(华中科技大学物理学院 湖北 武汉 430074)

1 引言

库仑定律与光子静质量为零有着密切的关系，当库仑定律严格遵守平方反比律时，光子的静质量严格等于零.反过来，若库仑定律出现偏差，光速将不为常量，光子静质量不为零，即使远小于电子质量，这样的结论都会对现有物理框架产生巨大冲击，这将会带来一系列原则性问题：规范不变性将不成立；电荷守恒定律将被破坏；麦克斯韦方程组将被普鲁卡方程组取代,等等[1].

本文从假设平方反比律存在的偏差出发，通过数学变换修正麦克斯韦方程，利用麦克斯韦方程组推导出光速的表达式，并与量子力学观点推导出的结果进行定性比较.

2 从库仑定律到光子静质量

库仑定律表述为：真空中两个点电荷之间的静电力与两点电荷电量乘积成正比，与它们之间距离的平方成反比,力的方向在两点电荷连线上，同性相斥异性相吸.

由库仑定律和场强定义式得出场源电荷Q在距离它为r处的电场强度大小为

若库仑平方反比律存在δ的偏差，修正后的表达式为

(1)

考虑到静磁场的麦克斯韦方程，有

实施绿色GDP，必须要改变目前的政绩考核机制。首先，对各地方政府官员的政绩考核机制不应该单纯的以GDP为核心，而应该以扣除环境污染成本之后的绿色GDP作为考核指标；其次，各地方政府官员应该消除地方保护主义的思想，加强对当地企业的监督管理，对不重视环境保护的企业应该加强惩罚力度。

(2)

假设电荷守恒，有

(3)

假设空间中电荷分布为:ρ=p(r,θ,φ)，记所取坐标原点为O，面元为dS，r处电荷到面元dS矢量为r′，r处电荷在面元处产生电场强度为E，面元法向量为n，α为R与r夹角，如图1所示.

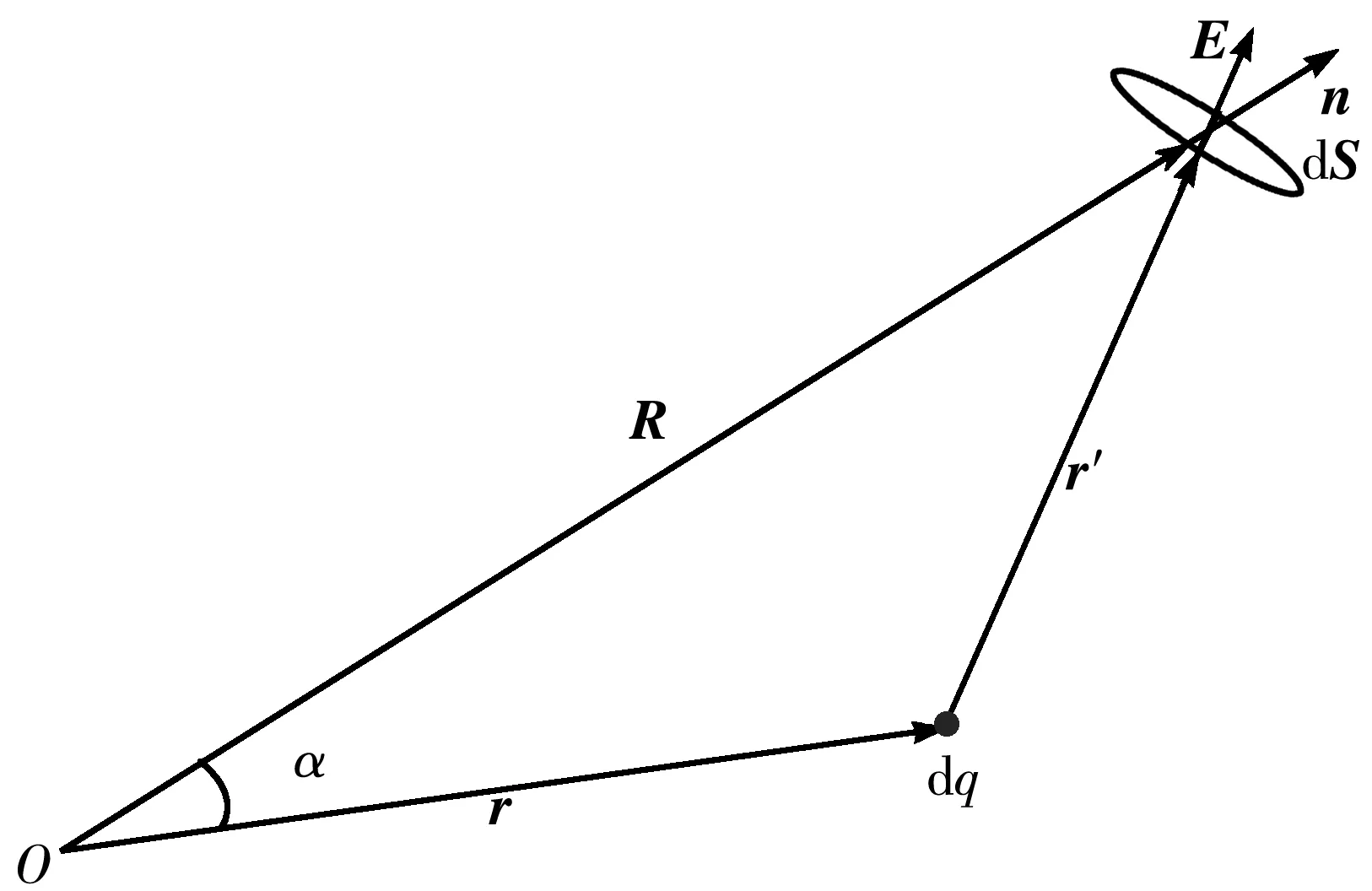
图1 体电荷元在面元的电通量

体电荷元在面元的电通量为

(4)

取半径为R的封闭球面S，由几何关系，并对式(4)在全空间积分，有

其次，加强宣传工作，营造良好的绩效目标管理考核氛围。为了能够使学校全体工作人员都能够以积极的态度和饱满的热情参加到考核工作中来，必须从思想意识领域使其意识到绩效目标管理考核的重要性与必要性，使其充分认识到所肩负的责任和承担的使命，只有在此基础上才能够营造出协同共进的绩效目标管理考核氛围，推动考核工作法顺利开展。

sinαdα=SE·dS

(5)

假设电荷分布在有限区域内的情况下，总能在有限空间找到一个足够大的面S，使得其包围所有电荷，ρ在S外取值为零，则式(5)化为

(6)

取电荷分布仅与r有关的情况，即

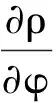
(7)

记

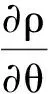
(8)

R2sinαdα

(9)

(10)

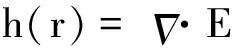
(11)

式(6)等价于

4.注重企业金融会计队伍建设。金融会计风险要想控制在一定的范围内，就先要建立完善的体系，强化参与人员的专业技能和基本素质，创建一支专业化的队伍，不仅在专业技能上要过硬，思想素质和个人觉悟上也要够强，只有这样，在外来诱惑面前才能抵御住。所以在培训方面也要对从业人员进行定期的教育，不仅仅是专业技能上的，还有思想道德上的。其次在人员的招聘上，也有制定严格的招聘制度，不用品德有问题的人，对于各方面都胜任的人员进行培养，同时岗位之间要进行划分，各个岗位间的职责要明确。

(12)

f(r)=rk

(13)

记

式中：m0表示小波函数；ω表示角向量；hk1是有限长度实数数列；k1=0,1,…,2N-1，为调整系数；N是小波阶数；e-iωk1是小波基。

(14)

(r+)2sinαdα

(15)

(16)

其中C1和C2为常数.

这时，掌声、唢呐声、锣鼓声停了。我一看，这些家伙真不够哥们儿，排得整齐的仪仗队自行解体，都悄悄地溜到远处指指点点——整个车站只剩下我们仨人。我知道四周有无数的眼睛向这儿望着，简直就像看马戏。

利用式(15)和(16)，有

(17)

其中C0为常数.

示意图如图2所示.

有

(18)

由于δ≪1，在δ=0处将g(r,R)展开并忽略二阶以上小量

(19)

可得

尽管现在从语义网上提取信息的技术有了很大的进步，但是产生的RDF知识库仍然存在大量的噪音和与事实不一致的问题，需要添加一些额外的一致性约束。本节就是根据扩展的有效时间的现实意义，分析时态RDF数据存在的不一致性，根据不同情况进行了分类，并对存在的所有类型的不一致性提出修复算法。

ln(r2+r2-2r2cosα)dα

(20)

对式(20)积分换元

取Δx→0，并写成偏导数形式，得

(21)

化简为

(22)

对于函数ξ(x)，以及δ≪1，有

ξδ(x)=1+δln[ξ(x)]

(23)

利用式(22)和(23)

(24)

利用式(17)和(24)

(25)

其中C为常数.

代入f(r)和h(r)有

(26)

考虑到δ极小，且由边界条件，取C=1.

可得到对非静磁场情况下修正后的方程

(27)

代入式(26)，由于此方程应在空间任意处成立，故可消去拉普拉斯算符，得到修正后的麦克斯韦方程

(28)

取电磁波传播方向为x方向，E矢量在xy平面内振动，B矢量在xz平面振动，振动方程分别为

E=E0sin(kx-ωt)

①关于“法律规定的机关”。从现行法律体系和有关法理上看，水资源保护公益诉讼中 “法律规定的机关”应当仅限定为各级水行政主管部门和检察机关。检察机关作为法律监督机关，当然具有提起公益诉讼的主体资格。水行政主管部门之所以应当具有水资源保护公益诉讼主体资格，理由：一是水行政主管部门具有保护水事公共利益的法定职责，基于保护水事公共利益考虑理应有权提起公益诉讼；二是水行政主管部门具有启动公益诉讼程序的便利性和及时性，在发现破坏水事公共利益案件、及时启动公益诉讼程序方面，具有天然优势；三是水行政主管部门具有设备、专业知识以及能力方面的优势，更易于通过诉讼维护水事公共利益。

(29)

B=B0sin(kx-ωt)

储罐火灾产生强烈辐射热，消防人员难以靠近。油罐火灾燃烧时高温可能使罐壁塌陷、破裂，储罐火灾统计数据表明，10 min内储罐罐壁温度最高可达700 ℃，罐壁钢板机械强度降低90%左右，此时储罐将发生变形和破裂，形成大面积流淌火及燃烧死角，一次性扑灭比较困难[6]。

(30)

又

图2 电磁波在空间中传播

在xE平面内取如图3回路，B方向垂直于xE平面，在x0处取长为dx，高为E(x0)的长方形回路，回路方向如箭头所示,示意图如图3所示.

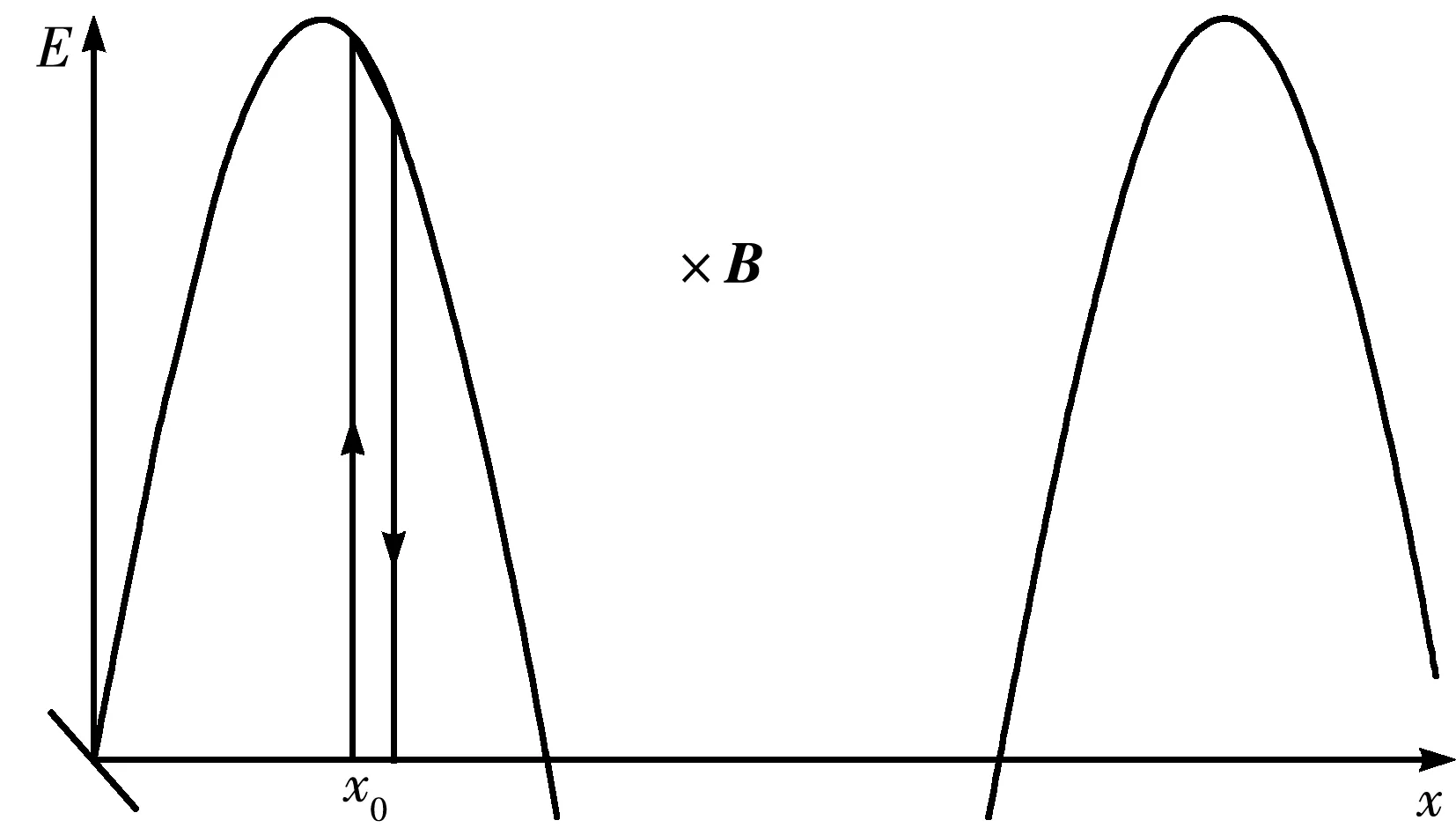
图3 电磁波在xE平面投影

将式(29)和(30)代入式(37)，得

(31)

将式(31)改写为

(32)

ln(r2+r2-2r2x)dx

(33)

将式(29)和(30)代入式(33)，得

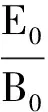
(34)

其中c为r处光速.

在电流密度j=0的场中，将式(28)写成积分形式，为

(35)

在xB平面内取如图4回路，E方向垂直于xB平面，在x0处取长为dx，高为B(x0)的长方形回路，回路方向如箭头所示，示意图如图4所示.

图4 电磁波在xB平面投影

利用式(35)，有

(36)

取Δx→0，并写成偏导数形式，得

(37)

由麦克斯韦方程

由图9分解结构图所示，并按照小波分解式(1)、式(2)，采用MATLAB小波工具箱对数据进行小波分解，采用双正交小波db3[14]作为母小波，对拱顶位移序列进行三尺度小波分解，可以得到低频序列a3，以及高频序列d1、d2、d3，如图10所示。

(38)

式(34)与式(38)相乘并化简可得

(39)

两组治疗后房颤负荷与心率均低于治疗前，且观察组治疗后房颤负荷低于对照组，差异有统计学意义（P＜0.05）；两组治疗后心率相比，差异无统计学意义（P＞0.05）。见表1。

相对论指出，静质量为零的物体速度不变，故当δ≠0时，光子静质量不可能为零.

3 从光子静质量到库仑定律

假设光子存在静质量为m0，光子能量动量应满足[2]

(40)

在核设施的辐射防护上，起初认为只要保护了人类，也就保护了其他物种。1976年，国际原子能机构(IAEA)明确提出非人类物种的保护问题，1990年国际放射防护委员会(ICRP)提出的在保护人类的同时还需要保护人类赖以生存和发展的其他生物的辐射防护观点逐渐为人们所认可。因此，从保护环境、维持生物多样性的角度，需要评价核设施对于生物的辐射影响。国外在该方面进行了较多的研究，并研发了专门软件，得到了广泛应用。

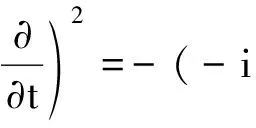
(41)

式(41)作用在电势函数φ(r,t)上

(42)

(43)

(44)

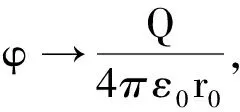
c1=0

(45)

(46)

将式(45)和(46)代入式(44)，得

另外，CSS缩写性质还能将多个性质/属性同时压缩进CSS样式表中的某一行列代码中。例如:smplel {margin-top:l6px;margin-r i g h t:2 2 px；m a r g i n-bottoma13px;margin-1eft:26px；padding-top:6px;利用CSS缩写性质后，就可将原来的代码缩减成：samplel{margin:16px、22px、13px、26px;paddmg 6px、12px、5px、9px;border-topahin solid #000000;}这样既不会影响到性质作用，还会扩大网页空间。

(47)

对φ求偏导，同时利用m<10-49g[3]，舍去小量，得

(48)

可以看出，当光子静质量m0≠0时，电场强度在平方反比衰减的基础上还存在一个指数衰减，平方反比律不再成立，其偏移项δ≠0，且随着r变化而变化.当且仅当m0=0时，偏移项δ=0，式(48)满足标准的平方反比定律.

4 结论

本文提出了一种全新的论证光子静质量等于零与库仑定律符合平方反比律互为充要条件的方法，若库仑定律平方反比律存在偏移，光速会随着电磁波传播距离变化，同时光子静质量也会随着传播距离改变，光子静质量由电磁波传播距离和偏移量决定，而改变趋势是由偏移量唯一决定的.

量子力学的结论指出，若光子静质量为定值，库仑定律的平方偏移量会随着电磁波传播距离变化，偏移量的大小由电磁波传播距离和光子静质量决定，而偏移量改变趋势由电磁波传播距离唯一决定.

本文对有源相控阵天线接收链路等效噪声进行了理论分析，并在此基础上详细推导出等效噪声计算公式，该计算方法中每个T/R通道的增益、噪声系数等技术指标都分别作用于最终结果，适用于任意变化的有源相控阵天线。该方法推导出的等效噪声计算公式已经在仿真及雷达系统中获得了实际应用，该公式有助于精确计算有源相控阵天线接收系统的性能。

但是值得说明的是，两者矛盾的来源是由于基本假设的不同，对于光子静质量为零的情况，两者不会产生矛盾，对于光子静质量不为零的情况，具体的结果还需要实验验证.

另外，对于光子静质量上限的估计实验到如今依然在进行着，2004年国际基本粒子数据组给出的光子质量上限为m≤10-49g[3]，比电子质量小了20多个数量级，由于光子质量如此之小，要从实验中得到光子静质量为零是很困难的，两个结论同时指出，在点电荷激发的场中，库仑定律和光速的偏差会随着电磁波传播距离的增加趋近于零.由此启发通过改进检测很小距离的电场的方法改进测试手段，提高测量精度.

对于光子静质量是否为零的讨论与验证会长期存在下去，这样不断修正理论，指导改进实验，同时利用实验结论完善理论的过程，无疑是非常有趣且有意义的.