Slacklining: A narrative review on the origins, neuromechanical models and therapeutic use

Charles Philip Gabel, Bernard Guy, Hamid Reza Mokhtarinia, Markus Melloh

Charles Philip Gabel, Research Section, Access Physiotherapy, Coolum Beach 4573, Australia

Bernard Guy, Ecole des Mines de Saint-Etienne, Saint Etienne 4200, Loire, France

Hamid Reza Mokhtarinia, Department of Ergonomics and Physiotherapy, University of Social Welfare and Rehabilitation Sciences, Tehran 12345, Iran

Markus Melloh, School of Health Professions, Institute of Health Sciences, Zurich University of Applied Sciences, Winterthur 8410, Switzerland

Markus Melloh, School of Medicine, The University of Western Australia, Perth WA 6009, Australia

Markus Melloh, Curtin Medical School, Curtin University, Bentley WA 6102, Australia

Abstract Slacklining, the neuromechanical action of balance retention on a tightened band, is achieved through self-learned strategies combining dynamic stability with optimal energy expenditure.Published slacklining literature is recent and limited, including for neuromechanical control strategy models.This paper explores slacklining’s definitions and origins to provide background that facilitates understanding its evolution and progressive incorporation into both prehabilitation and rehabilitation.Existing explanatory slacklining models are considered, their application to balance and stability, and knowledge-gaps highlighted.Current slacklining models predominantly derive from human quiet-standing and frontal plane movement on stable surfaces.These provide a multi-tiered context of the unique and complex neuro-motoric requirements for slacklining’s multiple applications, but are not sufficiently comprehensive.This consequently leaves an incomplete understanding of how slacklining is achieved, in relation to multi-directional instability and complex multi-dimensional human movement and behavior.This paper highlights the knowledge-gaps and sets a foundation for the required explanatory control mechanisms that evolve and expand a more detailed model of multi-dimensional slacklining and human functional movement.Such a model facilitates a more complete understanding of existing performance and rehabilitation applications that opens the potential for future applications into broader areas of movement in diverse fields including prostheses, automation and machine-learning related to movement phenotypes.

Key Words: Slacklining; Neuromechanics; Human movement; Model; Balance; Rehabilitation

INTRODUCTION

Slacklining is defined as a complex neuromechanical task involving achievement of functional independence while maintaining dynamic stability through balance retention.This occurs from the interactions of the individual’s whole-body where internal dynamics drive the response to external environmental changes, while treading on an unstable, three-dimensional moveable, tightened, webbing-band fixed at each end[1,2].The concepts explored in this paper consider and address what slacklining is, and its historical origins, in order to provide essential background understanding of the activity and its evolution, recognition and progressive incorporation into prehabilitation and rehabilitation.With this background knowledge, the existing explanatory models can be considered, how they apply to an individual’s capacity to achieve stability, and whether they provide a complete recognition and understanding of the explanatory control mechanisms for multi-directional instability and complex multi-dimensional movement.As such, they should be able to explain slacklining as a harmonious functional movement (HFM), namely the integrated interrelation of neural and muscular components to facilitate and enable a stable harmonized full-body functional movement[3].Examining these current models enables the determination and recognition that there are knowledge-gaps, which indicates that existing models must be evolved and expanded in order to encompass the broad conceptual circumstances that achieve slacklining stability.

THE ORIGINS AND ACTIONS OF SLACKLINING

As a trend-sport, modern slacklining is an adaptation of the ancient performing art of traditional rope-walking.Modern slacklining was initially started by climbers and outdoor enthusiasts in the 1960s and 1970s in the European Alps of Switzerland, France and Austria as well as in Yosemite National Park in the United States of America, where ropes and cables were replaced with adapted lightweight webbing and ratchet technology that incorporated an easier, safer and more elastic line[4,5].Slacklining was originally termed “line-walking” or “funambulaire” (the precursor term to slacklining) in Latin European regions and “Jultagi” or “Eoreum” in Korea as a representation of Central Asia[5,6].Slacklining has very ancient, established history and cultural traditions.The earliest records are insinuated as being possible from approximately 40000 years Before Christ (BC) when man first invented ropes[7].Consequently, the necessity and challenge arose to walk along these ropes to enable the completion of normal tasks in construction, movement along and between habitation sites such as cliffs and trees[8], for communication and social interaction such as crossing gorges as continues in the Russian Dagestan region, on the ropes of early Phoenician sailing vessels in ancient Crete around 1000 BC, and eventually for entertainment[4,9].More direct inference is made at approximately 20000 BC where, “line-walking” or “funambulaire” was an established societal activity in pre-ancient Greece, China and the Korean Peninsula[4,6,10].The earliest documentation appears to be in pottery and figurines of Cycladic acrobats from around 3000 BC[11]; and as a performance component of the ancient Greek Olympics from 776 BC and earlier Greek Games where the “Thaumatron”was awarded to those who performed a marvelous act or spectacle[6].

However, historical writings suggest the ancient Olympics were an extension of games from earlier periods, particularly the bronze age of Anatolia (3000-2500 BC), Crete (3000-1100 BC) and Mycenae (1600-1100), with some archaeological data suggesting games dated back to the 10thcentury BC[12].Funambulaire was an integral social performing art from at least 3000 BC[4,6]; and demonstrated in the fresco paintings of Selini funambulist rope-walkers from the Villa of Cicero in Pompeii’s ash covered ruins estimated as approximately 100-50 BC[13].The natural progression from ropes and cables to ratchets and webbing reflects human evolutionary capacity found in multiple incorporations and replacements of traditional and established items into modern product developments and activities[8].The graded incorporation into rehabilitation could have been initiated at any time, but medical literary writings insinuate at least around 150 Anno Domini (AD) during the period of Imperial Roman (31BC-AD476)[10,14], while the first published papers were in European sports science literature around 2009[15,16] (Figure 1).

SLACKLINING: EXERCISE, REHABILITATION AND THERAPY

Slacklining in exercise and rehabilitation

The incorporation of such a fundamental yet physically complex recreational or cultural activity into the fields of therapy and rehabilitation is another evolutionary reflection.Slacklining, as therapy, has only been formally investigated and documented in the published scientific literature over the last decade[15-17].There is anecdotal evidence of slacklining’s therapeutic use since the 1970’s and 1980’s as both prehabilitation and rehabilitation for Alpine sports and athletes.This includes Ingemar Stenmark for downhill slalom ski[15], within Australia’s competitive surfing community and elite training programs that led to the high performance center at Casuarina on the Australian East Coast[2], and for rock-climbing[17,18].However, its first recorded application may be inferred from the Greek-Roman physician Galen-of-Pergamon from 150-200 AD.Galen is recognized as the father of “Exercise in Medicine”[10,19] with over 500 medical Treatises[20] that provide potential documentation for the use of rope walking for rehabilitation and prehabilitation purposes.The texts considered[21-23] do not mention rope walking specifically as an activity, but such an activity or exercise is highly likely to have been used and can be insinuated from the following knowledge: rope walking was, as mentioned, an accepted and integral activity within Imperial Roman Society[4,6]; Galen is considered the “father of rehabilitation” who advocated the importance of exercise, his texts and teaching were the recognized authority for almost 1600 years[24], particularly for exercise and health[22,25].Galen wrote extensively on knee injuries including loss of function and balance in athletes and Gladiators, noting that knee muscle control required considerable time to regain due to loss of muscle activation, with “wasting in the absence of local muscle or nerve damage”[24], a reference to arthrogenic muscle inhibition (AMI)[6,11,14,18].Galen prescribed exercise for rehabilitation and prehabilitation as essential for “… health and good condition”[26], and ”… strength for function”[19,22].Consequently, though not specific in detail, slacklining could have occurred through the informal or guided inclusion of an existing, recognized and challenging balance activity.Consequently, the incorporation of slacklining into rehabilitation may not be “that” recent, but actually date back some 2000 years.

Slacklining and arthrogenic muscle inhibition

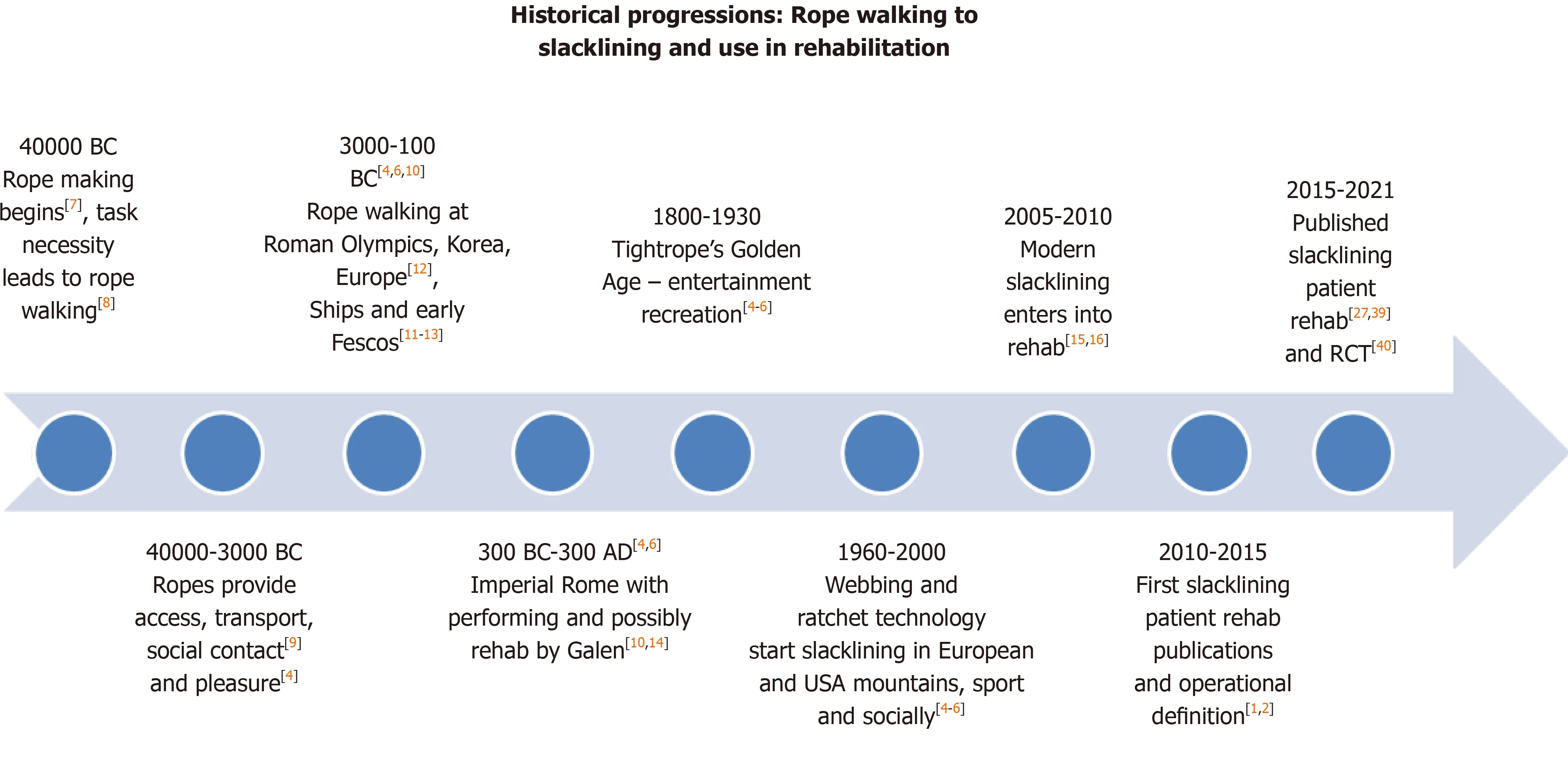
Figure 1 Historical progressions: Rope walking to slacklining and use in rehabilitation.

The discussion of AMI is an important consideration as slacklining appears to negate the local muscular inhibitory action, particularly in the knee quadriceps[2] and potentially in the spinal lumbar multifidi[27].AMI is defined as muscular activation failure, about a damaged or distended joint, due to ongoing neural activation deficit[28,29].AMI has been well recognised since at least the 19thcentury as having a central-neural basis[30], being a consequence of articular sensory receptor discharge from joint afferents[31] due to swelling, inflammation, joint laxity[32] and tissue damage.The presence of AMI is consistent across different joints and joint pathologies, particularly the knee[29,30,32,33], hip[34], elbow[35], shoulder[31] ankle[36] and intersegmental spinal muscles[37].Evidence indicates that with AMI, supra-spinal pathways potentially play a significant role through inhibitory down regulation that affects central nervous system (CNS) neural inhibition, that in-turn prevents full muscle activation.This is in conjunction with spinal reflex contributions through the Group-I non-reciprocal inhibitory pathway reflexes including the flexion and Gamma (γ)-loop[28].Today, the full understanding of AMI remains incomplete and is the subject of significant investigative research[38].However, slacklining’s recognized effect in over-riding this down regulation, in the lumbo-pelvic[27] and lower limb regions[2,18] is gradually being recognized and is a significant advancement in anatomical and condition specific regional rehabilitation[39,40].

Slacklining as therapy

The therapeutic direction of slacklining has evolved over the past decade to become an adjunct in both injury prevention, such as falls in the elderly[41], and specific sports including judo[42], basketball[43], badminton[44], handball[45], and football/soccer[46]; as well as in rehabilitation[2], including orthopedics[2,27], neuro-logy[27,39,40], sports training[47], general physical training[46] perfor-mance[43], and recreation[5].This inclusion of slacklining with other prevention and rehabilitation themes derives from the triad of sensory system contributors of proprioception, vision, and vestibular somatosensory inputs[48].This is a consequence of the unique properties of slacklining[2] due to its distinct action from other conventional balance activities[49] and apparatus[41,43] as a composite-chain activity,i.e.there is a weak link in the kinetic chain resulting in abnormal motor synergy patterns due to the contact surface of the loaded limbs having free, partially supported but unstable movement on a recoil resistance surface[50].The coupling of these qualities and the CNS contributors results in slacklining having four integrated qualities[2]: Balance - the equilibrium control regulating the body’s segmental dynamic movement and center-of-mass (CoM) within the base of support[51]; postural control - the body's positional control in space[52]; muscle strength - the muscular generated forces[43,53]; and neuromechanical demand - the integration of neurobiology and biomechanics[1].

MATHEMATICAL AND GENERAL MODELS THAT EXPLAIN SLACKLINING

Manifold models

It is recognised that the neuromechanical control strategies employed during slacklining are not fully understood[54].Several detailed proposed models seek to explain slacklining and predominantly utilise a conceptual “manifold model”.However, the term manifold has two denotations: firstly, within a general context as a “conceptual dimension inside a general discussion”; and secondly, within a mathematical context as a “mathematical subset with lower dimension inside a mathematical model”[55].The latter context is a defined shaped space where all activity and analysis occurs[56], which for slacklining likely simulates a saddle-shape within ordinary task space[57].This saddle-manifold is shaped concave in the dimensions of the direction of the slackline (X) and convex in the direction of its lateral shift (Y) and the dimension of gravity or sag (Z)[58,59].

Scientifically and mathematically a “manifold”has the same or lower dimensionality as the underlying mathematical model, though mathematically the number of dimensions possible is arbitrary.Each point within the manifold has its own “homeomorphic” space.Consequently, a “bi-continuous function” exists between all points being on both a continuum in a given direction, while concurrently having an opposing continuous inverse function[60].The manifold model concept was initially proposed within robotics as the “self-motion manifold”[61], and, subsequently applied to human movement and functional tasks as the “un-controlled manifold” (UCM) model[62].Such a model suitably explains quiet-standing[58,59] and simple functional frontal plane movementse.g.,walking and postural sway[57,63], but was not proposed for complicated tasks involving dynamic contact,e.g.,slacklining[1,54].

The UCM may still, however, provide a potential solution as it proposes a motor control strategy for redundant systems by using the abundant solutions inherent to them[62].This postulates that the task redundant space of the effector is not homogeneous,but structured according to task requirements[61,64].Consequently, the UCM model may be expanded to accommodate slacklining as the increased variability and redundancy found in such challenging actions can be redistributed, allowing acceptable levels of task variability to be maintained[56,65].

In human quiet-standing and frontal plane movement on stable surfaces, the Newtonian equations in classical mechanics of an inverted pendulum are generally considered acceptable mechanical models for self-balancing[51,59,66].These considerations are critical in acknowledging“how”the body estimates its current orientation in space, in order to, subsequently, generate the corrective stabilizing actions required to maintain what is a mechanically unstable upright stance.However, for slacklining, this model is not suitable.The base is not fixed: Consequently, body neuromechanical dynamics are coupled with the slackline’s external dynamics, and the natural actions and subsequent responses of body-sway[1,54,67].

Application of the manifold model to slacklining

To consider these attributes within a global encompassing model to describe slacklining as a dynamic and changing series of quantitative factors, Paolettiet al[1] proposed that “an optimal strategy is achieved”for self-balance.This is through the consideration of a nonlinear model that accounts for potential parameter coupling and overall CNS performance delays that occur on multiple time scales.These can be visualized as a system with passive coupled dynamics working in unison with sensory modalities, enabling orientation and activated motor coordination of the body to be self-directed or “inferred”.In Serrienet al[68], where the balance strategy was examined within an “expanded manifold of a higher dimension” that the subjects must remain within, this approach in turn enabled the model to account for coordination from the perspective of “self-organizing maps”[68].This modelmodification allowed an entire kinematic chain response where equilibrium is achieved as an integrated CNS solution to the presented task-environment-subject dependent situation and allows for a large set of degrees of freedom (DoF) that facilitate understanding of postural control within the human motor system[69].Additional perspectives from Valleryet al[53] clarify that these neuromuscular actions involve a decoupling of the stance leg/s, and its produced vector forces from the residual body, through muscular co-contraction at the hip.This is augmented by arm movement and bimanual arm coordination[70] that act as the primary initial compensatory reaction to CoM displacement[47], and in turn the arms concurrently provide angular momentum influences[54].

BALANCE AND HARMONIOUS FUNCTIONAL MOVEMENT

In the balance model for achieving slackline independence through human HFM, the manifold’s defined space contains variables with a significant set of DoF that contribute to particular movements or functions[69], some of which provide the amalgamation of stability and mobility[3] through CNS control[56].Consequently, the model’s manifold contains both stable controlled variables and unstable un-controlled variables, where no action control is required as a task-variable’s position is not affected[62].Any given set of CNS controlled DoF that provide stability, consequently, have variables separated into two orthogonal/opposing-directional subspaces: one with actions that have no effect (on the controlled variables); the other with orthogonal-subspace actions that do[62].If variability in the controlled subspace is smaller than that of the opposing orthogonal-subspace, then the CNS, and, consequently, stability control, is unaffected[56].These manifold models simplify reality[1] and enable a mathematical representation and analysis.They also provide insight into what CNS control aspects are present when postural balance strategies are implemented[71,72], and that all responses occur within physically defined boundary limitations[47].

SUMMARY

The outlined existing hypothetical models of slacklining describe the neuromechanical control strategies that achieve this activity, predominantly through use of a conceptual “manifold” that simulates a “saddle-shaped” task space[58,59].Through the use of classic mechanics this is envisaged as a self-balancing mechanical model of an inverted pendulum[51,66].These concepts critically acknowledge spatial orientation and subsequently corrective stabilization actions.However, this is generally hypothesized around a stable or fixed base which is inadequate for a body dynamically coupled with external changes and response actions[1,54,67].Consequently, there is a knowledgegap and a required evolution and expansion of these ideas, not only from the perspective of mechanics[1,51,54], but also from that of the neurological[73] and biopsychosocial[74] constraints of the individual.

PHYSICAL FORCES AND ORDINARY SPACE

Existing models of harmonious functional movement

Models of human HFM and self-balancing generally consider two concurrent spheres of input: firstly, mathematical mechanical precision models bound by classical mechanics equations and; secondly, supplementary sensory and motoric neural control[47,67].The mechanical models were initiated over the last 600 years, most likely from Da Vinci’s documented model proposition:“motion is created by the destruction of balance, that is, of equality of weight, for nothing can move by itself which does not leave its state of balance, and that thing moves most rapidly which is furthest from its balance”[75].In contrast, the importance and relevance of the control aspects of a neural source were not proposed till the mid to late 1800’s, when the understanding of sensory input and neural latency were detailed in seminal German publications.

The initial aspects of sensory control include the perspective of frames of reference as used by the nervous system, and the kinematic constraints that these place upon any control aspect.Initially, this came from the role of vision and was established from Donders[75]’ Law, namely “that there is a unique orientation of the eye when looking in any specific direction”[76].This was supplemented by Listing's law which “… specifies what this orientation is”[77,78], being a principle that governs eye movements through the three dimensional (3D) planes of horizontal, vertical, and torsional,and is actively implemented by a neural mechanism[79].Fick[79] proposed that Listing’s law enhanced motor efficiency by “minimizing the rotational eccentricity of the eye”[80].This sensory-motoric control system was quantified by von Helmholtz[80] who measured the time delay that occurs due to the finite speed of neural signal transmission, where response time is dependent on the input-output delays of single neurons and neural chains.Donders[81] furthered these control phenomena in his work related to “The speed of mental processing”,which determined a relationship was present between an individual’s “choice-response” and the number of stimuli present[82].This was, subsequently, supported and progressed by Merkel[82] who defined that “the response time is longer when a stimulus belongs to a larger set of stimuli”.This eventually led to Hick’s Law[83], or the Hick-Hyman Law almost 100 years later that proposed “…information is intimately concerned with reaction time” and describes “… the rate of gain of information”, and assesses the involvement of “cognitive capacity”[84].

The Hick-Hyman Law denotes that the time an individual requires for decisionmaking results from the choices available, and will increase logarithmically with the number of choices.In slacklining, these choices increase dramatically compared to simple frontal plane movements[54,57,63].Consequently, transmission rates vary significantly between cell types and transmission mediums being affected by neuron size, the presence of axon myelination and its composition[85], sheath number, length, thickness and distribution[86], the size and distance between nodes of Ranvier, types of intervening synapses and how many occur between the CNS and peripheral receptors, and the stimuli strength, and quality[85,87].The sphere of task control and the time-delay present is due to the sensory and motoric neural pathways necessary signaling processes, such that delay increases as the system and its requirements become more complicated[58,73].This accounts for the balance organ with the integrated labyrinthine and vision systems that are adapted to account for these time delays[67], and ensure the essential limitations necessary for the human body to remain stable[64].

This is particularly relevant for more complex movements, such as those that occur on unstable surfaces, at higher speeds and require greater skill, with slacklining being such an example.Accordingly, in human movement, the more complex the task and the more stimuli present, the slower the action[17,88] or the greater the response time, Fitts’s[88] Law (Table 1), and the higher the neuronal firing rate[1].Further considerations are the large variation in effects of normal and pathological ageing[85] on human mechanical structures[67,86], neural system time delays[64]; and that injured tissue and individuals at the global level (such as neurological conditions) will not be able to achieve the required levels of adaptation, and, consequently, the individual will exhibit postural deficiency or balance loss[53,89,90].The overall consequence is a simplified large-scale time-delayed model that provides insight from classical mechanics into the integrated functioning of the body systems and organs that support the theories and hypotheses of “integrated control”[48,67].

The subsequent progressions in the mathematical mechanical human movement and self-balancing models came at the start of last century when Graham-Brown[90] reported on “dynamic principles involved in progression”.He stated that: “The cycle of progression may be supposed to commence at a point at which one of the limbs is perpendicular to the ground.The “initial velocity” then carries the body past this point, and it then falls forwards along the circumference of a circle the radius of which is the limb in contact with the ground”.Over the last half century there has been further evolution and progression with Bresleret al[91] who remarked that the “Dynamic balance of the “head, arms and trunk” about the supporting hip is dependent upon the control of pelvic motion by the hip musculature”; while Saunderset al[92] recognised the significance of “Pelvic lateral tilt (being) identified as one of the primary determinants of gait”.

In 1971, Adams[93] proposed the Classical model of “…a closed-loop theory for learning simple movements”, that incorporated feedback, error detection and error correction as key elements.This model required that the output of the system had feedback, and compared the reference for error detection and, if necessary corrected for this to provide the resulting movement, such that it was “… self-regulating by compensating for deviating from the reference”.More recently, MacKinnonet al[50] described “Control of whole body balance in the frontal plane during human walking” through the model of the “inverted pendulum” which relies on the principles of equations from classical mechanics.This model was progressed through a series of evolving modifications to account for the influence of both random disturbance and control torque.This neurologically controlled delay is effectively present at the ankle joint due to the concurrent relationship between: the passive stiffness from the viscoelastic nature of the muscle-tendon-ligament complex; and the active modulating influence of regional muscles[73].This is supplemented by the triceps surae muscles that maintains balance by ”predictively controlling the proximal offset of the springlike element in a ballistic-like manner”[94,95].

Within the mechanical model it is also critical to consider that the inherently unstable upright position, where the smallest deviation eliminates equilibrium, is retained through uniformity between retarding and controlling forces[67,96].These provide contributing components that can be low-level, such as passive ankle stiffness,vshigh level, such as the growth-rate of the gravitational toppling torque[58,95].Together these forces are considered a simple closed-loop control model[48] as a progression of Adams “closed loop” model[94].A further mechanical model input consideration integrates neural sensory aspects, where feedback mechanisms are based predominantly on body-sway motion[63] from balance perturbations[97].These evoke “sensory weights”, a form of neural control representing comparative contributions of each sensory systems and integrated as a “package”[48].This provides an internal estimate of orientation[71], where the assessed and adjusted responses are determined by how these inputs contribute to the total balance system as a single component[1].Consequently, this “package” is itself dynamic and varies sufficiently to ensure equilibrium and prevent instability from corrective actions being either over- or under-produced[48].The inputs themselves therefore exhibit bi-fold competing variations, due to the quality of the sensory information received.This is a consequence of changes in: (1) The external environmental conditions; and (2) The internal conditions affected by injury, neurologic disorders[90,98], or other psychosocial factors[65,74].In the presence of a moving platform, as with slacklining, the vestibular and somatic sensory feedback is more highly weighted; while in quietstanding the proprioceptive and visual systems are dominant[71].Further, during afferent motor control the CNS creates“muscle synergies” where groups of muscles are combined as a common neural signal to control a range of movements which can be modulated differently by each individual, consequently demonstrating the neuromuscular capacity for adaptive strategies to facilitate stability while slacklining[99].This reinforces the findings of neuroplastic change, automatic or “packaged” signals[48,71], engrams[100] and homunculus smudging[37], all of which occur as a response to complex, demanding, balance challenge activities[100], which will, consequently, include slacklining[2,101].

Table 1 Glossary of definitions and explanation of scientific terms

The consequential reactive motoric action that produces the stability, in the mechanical paradigm perspective, is achieved through the generation of joint torques that appropriately correct for any deviations from a desired orientation[48,72].The original perturbation changes are detected primarily by inputs from the visual, proprioceptive, and vestibular sensory sub-systems[67,71], with the resultant reflex delay[1,72] enabling a “Hopf bifurcation point”[2] (Table 1).This achieves a temporary, though dynamic, “solution”for equilibrium and self-balance, with suitable active control strategies[58,67].This “equilibrium solution”is explained by both the mechanical and sensory aspects within a“saddle-like” 3D phase-space that is characterized by geometrical properties and spatial relations of position and velocity[58].It is achieved through the optimal parity between two competing manifolds: one which is stable along the saddle and provides slow convergent motion in a direction toward the equilibrium; and the other which is unstable and provides divergent spiral motions such as pitch, roll, and yaw[97] about the axis of the phase planes, which further increase the number of dimensions and DoF present, as these actions occur in directions away from the equilibrium[58].This “solution”is overseen by an intermittent“proportional and derivative”feedback system controller, that is characterized by the switching function at the “Hopf bifurcation point” in such a way that the proportional and derivative control is“off” when the net force is near the stable manifold of the saddle and is“on”in all other circumstances.This controller is able to use considerably smaller regional space and feedback parameters, which make it more robust[58] in the designated phase plane, as it exhibits the “two-thirds power law”[3] (Table 1) scaling regimes typically found in physiological sway movements in humans.Concurrently, the nominal equilibrium state is itself surrounded by a “dead zone” that reflects the time-delay from the sensory neural control inputs[72] that will allow a motoric reaction[64] that provides spontaneous movement patterns, like sway, to occur[95].As a simple feedback loop system, this can provide an acceptable model for dynamic stability to ensue[52,58].It also accounts for: Age-related differential findings due to physiological change - such as passive joint stiffness and damping from osseous degeneration, and proprioceptive delay, which affect center-of-pressure-based sway behaviors[57,66]; plus notably increased “noise” from larger amplitude, plus false and extraneous input signals[57,73] that can all be viewed from a “classical mechanics”influence perspective[67].

Any integrated mechanical and sensory model must also consider and discuss optimization approaches occurring, concurrently, within both aspects of the model, and that account for the “smoothness” or “flow” of HFM[3,102],e.g.,compare a curve joining multiple points to a series of straight lines.This smooth, HFM is a consequence of the process of “speed-curvature coupling”[103] which is optimized by the coordinated brain action of sensory and motoric control under the influence of preplanning and “temporal segmentation”, the process that “…identifies motion breakpoints and separates the different constituent phases”[104].These sensory considerations are based on the mechanical assumptions of Riemannian or elliptic geometry[4,103] (Table 1).There is also a need to consider geometrical transformations that are both “affine”[5] (Table 1) and “equi-affine”[6] (Table 1), particularly in unstable settings, such as on a slackline, where the involved rotation, translation and shearing actions are both achieved and minimized in order to provide constant speed[102], such as occurs in the jerk response or Hoffman reflex[105].

This is of significant importance in relation to sensory input, particularly visual processing, as it confirms that “temporal segmentation”[7] (Table 1) of movement control complies with “equi-affine geometry”[103].This geometrical transformation consequently accounts for the “two-thirds power law”, which governs the relationship between the geometrical and temporal parameters of human movement.This is centrally represented in “motion-planning”[61] and “human vision processing” and ensures that the “Isochrony principle”[8] (Table 1) is upheld[103].This, consequently, allows for the application of differentiable manifolds of higher dimensions, an important consideration for complex activities on unstable mobile surfaces, such as slacklining.The consideration of these additional aspects within a mechanical model clarifies that human locomotion complies with the principles of “Kinematic redundancy”[9] (Table 1); and the “Inter-segmental law of coordination”[10,103] (Table 1).

Together, these multiple aspects and considerations form the sensory and motoric neural control sphere, as noted previously from 18thCentury German scientists, concepts that were, subsequently, integrated with the mechanical sphere.In unison they explain functional independence and balance control as the aforementioned closed-loop feedback system[94], with parity between the different integrated sensory orientation source information on one hand, and system feedback control constraints on the other[48].However, such a conceptual model and presentation of balance, functional independence, and postural control, is only truly valid on stable surfaces[58].When unstable surfaces, such as a slackline, are considered in such models, then further descriptive initiates, progressions, and evolutions are required[1,54] to account for the dynamic changing postures and positions[2,27,106].This has led to the concept of “dimensionally-bound” manifold models, which require that the size-volume of the manifold is expanded.This accounts for the patterns of movement, control and balance-retention, that require higher levels of complexity within the significant DoF available for human motor system postural control[54].

THE CURRENT DESCRIPTIVE MODEL OF SLACKLINING

The concept of functional independence and self-balance being explained by dimensionally bound models, with expanded size-volume, takes into account activities such as slacklining that are significant progressions from those found in quiet-standing and simple frontal plane walking.This complexity occurs through the forces being produced more rapidly with the requirement for greater control occurring through smaller, more precise action-reaction dissipation[68].There is a simultaneous reduction in both frequency and velocity in most available DoF, coupled with increased control of range of motion (RoM)[69].This expanded manifold model allows greater distance in the Y and Z dimensions for any given X dimension position, but is limited by the physical constraints of the given slackline length (X dimension), its width and how far it can be moved laterally (Y Dimension) and the elastic-stretch that enables an optimal sag (Z Dimension).Consequently, a minimal effort or energy expenditure must be achieved and utilized to maintain stability in the presence of any perturbation[47].This is consistent with the strategies of quiet-standing and stable surface walking[70].However, any perturbation must be limited within the Y Axis, or lateral component of movement, to a distance in the order of 10 cm, for novices to moderate skilled slackliners, if control and balance on the line is to be retained[47].Expert slackliners appear to exhibit greater lateral movement limitations within an expanded manifold[69].

This 3D model form has been envisaged and detailed with mathematical equations to validate positions[1,58].However, to compound the descriptive difficulty of the model, it must be recognized that the optimal adopted strategy is individually selected.It can only be one of two methods prior to the introduction of any perturbation: (1) Two feet on the slackline, including use of an unloaded limb to touch and stabilize the line; or (2) One foot[2,5], with the other not touching but as a counterbalance that indirectly affects the manifold of the contacted and weight bearing foot[47].In recognition of this deficiency the model was subsequently modified[54] through introducing a regional decoupling at the hips of the arms and trunk from the legs.This then accounted for the discrepancy that action-reaction forces generated by the arms, trunk, or free leg, could influence the point of contact, without moving the foot or changing the anterior-posterior direction by virtue of sheer forces, and ensures the principle of “energy optimization” was maintained[54].This then allowed for individual joint torque and segmental interplay, where there is task distribution between the legs as the ultimate dissipater of the force vectorsviathe CoP dynamics at the foot/feet, but decoupled at the hips from the trunk and arms that influence, but do not control, angular momentum[47].

This 3D model then has the context that simulates the following example: an inverted pendulum[51] (the person), mounted on a cart (the slackline), that is moving on a circular or elliptical track[1] (the physical finite 3D ordinary space limitations of possible slackline movement), to a maximal distance from the slackline contact point[47] during instantaneous stability.Concurrently, the segments of the arms and trunk facilitate angular momentum control, and are decoupled by muscular co-contraction at the hips from the stance leg/s, that dynamically direct the vector forces[54].

The acquired movement control to achieve balance on a slackline is a set of selflearned patterns[96].These form an instantaneous but fluid and interactive dynamic saddle-shaped manifold[58] that the individual must remain within to ensure stability[69] through balance control[66].Stability is retained by the production of forces that are pro-active and re-active to those of the slackline’s 3D reciprocal forces at and through a point/s of fixed contact with the bodyviathe foot[47] or feet[47].Consequently, the slackline’s reactionary forces line of action always passes through the subject’s contact foot/feet and cannot be influenced without a dissipated moment from the force vector.This force,viathe foot to the leg, is in the X-dimension or anterior-posterior direction[54], the Y-dimension of lateral deviation within the physical limit of the slackline’s topographical space[47], and the Z-dimension of available sag or reactionary bounce[107].These forces form within the “highdimensional manifold” “… in which the subjects have to stay in order to maintain balance”[68].

The expansion of this manifold can be learnt, with the improved balance then interpreted as enabling an increased RoM before the manifold edges are reached and balance is lost.Because the expanded manifold’s edge is now further, the frequency of movement change is lower, as the need to adapt or change is less, which in-turn leads to a reduced velocity of motion and less kinetic energy being required when reaching the manifold’s edge.Consequently, maintaining balance is easier and the energy used to counter the perturbation is dissipated in a stepwise manner[47,97].

FACTORS THAT NECESSITATE CHANGES TO THE CLASSICAL MECHANICS MANIFOLD MODEL

Currently, the models of HFM and self-balance are limited to those described above.They can account for all available DoFs as found with dynamic unpredictable movement on unstable surfaces that consider and account for kinematic redundancy in consort with inter-segmental coordination.

This can be summarised as follows: An integrated mathematical mechanical precision model, bound by classical mechanics equations in parity with sensory and motoric neural controls that approximates a dynamic “saddle-like” phase-space, highdimensional manifold characterized by two internal competing manifolds of convergent and divergent motion.

This hypothetical model facilitates understanding the mechanisms for independent HFM and balance.These mechanical and neural components increase their complexity when considering the influence of “qualitative-implicit-knowledge”, such as the physics of gravity[108].Generally, the brain hypothetically uses a qualitative internal model that incorporates classical mechanics-based equations from its existing knowledge of gravity and time as a multi-faceted perspective that include a quantified unit and both a spatial and cortical experience, even if this knowledge is quantitatively based[108].This supplements sensory information when estimating more complex activities that involve external components, and not simply a body activity in isolation, including interceptive actions like hitting or catching[109].However, when performing a “catch” in zero-gravity, movement is initiated earlier[109] as “qualitative-implicitknowledge” is relied upon to pre-empt and approximate interceptive timing through pre-information that compensates for “no-gravity”[108].This is analogous to core muscle pre-activation when using a limb.Further, “qualitative-implicit-knowledge” is influenced by the individual’s psychological state, motivation level, past activityspecific experience, the social context where the activity is performed and the presence of positive support or negative perceived social pressure to participate or “perform”[53,74].Current movement models do not accommodate or acknowledge these additional aspects.By considering a highly skilled complex activity, such as slacklining as opposed to quiet standing, the intent is to consequently, recognize the areas of knowledge-gap so an evolved and expanded hypothetical model and paradigm can be proposed.

CONCLUSION

The successful achievement strategy that enables an individual to balance and remain on a slackline is currently explained as: A saddle shaped manifold model, where a moving inverted pendulum is subjected to self-generated and environmental forces within a defined 3D space, where the arm and trunk segments provide dynamic force influences but are decoupled from the hips and legs.This model integrates with gravity and the slackline’s elastic reactive properties being governed by classical mechanics.However, there remains a knowledge-gap as this dynamic stability is transitory, momentary, and acquired through the integration of additional dimensions not hereto considered.Consequently, within the context of historical and contemporary slacklining, the existing models are insufficient for the required explanatory control mechanisms that can accommodate multi-directional instability and complex multi-dimensional human HFM.This knowledge-gap requires an evolved and expanded model in order to provide an explanation for the control mechanisms in place.This evolved model will represent multiple, integrated dimensions that will facilitate the understanding of existing performance and incorporate general and rehabilitation activity.With such a model these applications can be applied more broadly in the future to movement in diverse fields that would potentially include prostheses, mechanized automation, altered gravity, robotics, mechatronics, artificialintelligence-driven movement and machine-learning related to movement phenotypes.

ACKNOWLEDGEMENTS

The author group acknowledges and specifically thank Dr.Ben Serrien for his invaluable input in the areas of physics, classical and quantum mechanics and assistance in manuscript editing.Without his input this article would not be completed.