基于有限元分析的某型雷达天线舱框架的拓扑优化减重设计

陈 弼，叶 堃，杨春鹏，李高杰

（中国船舶集团有限公司第八研究院，南京211153）

0 引 言

在雷达总体结构尺寸确定的前提下控制结构的总质量，对其进行轻量化设计可大幅提升装备的综合性能。目前，轻量化设计主要体现为结构优化、材质轻量化及力学性能最优化。相对而言，结构优化更为容易实现。通过有限元分析软件拓扑优化求解是取得结构优化的重要手段。

天线舱框架是旋转型相控阵雷达的重要组成部分，其静态与动态特性直接关系到整套设备的稳定性和安全性，在进行结构设计时希望能在满足基座刚强度的前提下尽可能减轻其质量。本文结合天线舱框架的实际受力情况，使用三维设计软件NX与有限元分析软件对结构进行拓扑优化设计，并对改进前后的基座静态和动态特性进行对比分析论证。

1 拓扑优化理论

拓扑优化的目标是在最大应力和最大位移保持不变的前提下尽可能减小结构的质量，即充分利用材料实现结构轻量化。结合有限元法的拓扑优化本质上是一个设计空间单元有无的问题，通过迭代计算，保留对结构传力性能有利的单元，删除对结构传力作用不大的单元，最后得到满足要求的较优结构。

ANSYS也是将拓扑优化问题转化为一种特殊形式的形状优化问题。优化的目标是在一定约束的情况下寻求结构的材料最有效性，对目标（体积、全局刚度及自然频率）取最大或者最小值。在拓扑优化中，结构的材料分配功能为优化参数。使用者需要定义结构问题（材料属性、有限元模型、加载等）、目标函数以及状态变量。

拓扑优化的理论是在限制条件（gj）定义下寻求最大或者最小的目标函数（f），在拓扑问题中设计变量赋予每个有限单元（i）内部伪密度（ηi）。伪密度值为0－1，ηi≈1则代表材料应该被保留。总体积就是所有单元体积之和，V＝∑iηi Vi。伪密度影响每个单元的体积和弹性张量，[Ei]＝[E（ηi）]。在常用的线弹性方程中，弹性张量用来等价于应力应变矢量，{σi}＝，其中{σi}为单元i的应力矢量，{εi}为单元i的应变矢量。

以求最大静态结构刚度为例，在体积约束的条件下，求最大结构刚度就是在给定载荷下寻求最小静态变形能，即

式中，uc为柔顺性N为单元数量；V为计算体积；V0为原体积；V∗为被除掉体积。

对于多负载条件下，求最大刚度问题可表达为

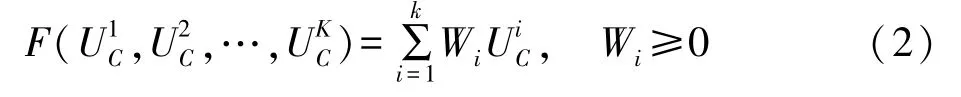
式中，为第i种载荷下的柔顺性，Wi为最小变形能的载荷分量。

基于以上理论，用Workbench中的Shape Optimi⁃zation模块对有限元模型进行拓扑优化。以单元材料密度为设计变量，体积减少百分比为约束函数，以结构的柔顺度最小化作为求解的目标函数。［1］

2 有限元分析

2.1 建立有限元模型

使用三维建模软件NX进行天线舱框架的三维建模。在此过程中，结合圣维南原理［2］对框架的部分倒角、凸台及螺钉孔之类的结构进行了适当简化，既不影响基座的强度和刚度，又提高了有限元分析的效率。

将框架三维模型以NX原格式导入有限元分析软件中，坐标系设置为默认坐标系。按照设计要求，框架壁厚均匀，内部布有十字交叉加强筋，所使用材料为防锈铝5A30，取其弹性模量E＝1.96 GPa，屈服强度275 MPa，泊松比λ＝0.28，密度ρ＝2 700 kg／m3。

2.2 网格划分

由于模型体积较大，采用自由划分网格往往失败，选择大的单元会对计算结果产生较大影响，采用太小的单元会导致计算时间过长。根据计算经验，网格划分方法为Hex Dominant，同时将Relevance设置为100，对内部筋板的单元大小定义为20 mm。

2.3 边界条件简化及载荷

本文根据天线舱框架实际使用情况对模型进行如下约束与加载，如图1所示：

（1）在框架底面法兰的螺栓孔处施加固定约束；

（2）重力加速度G，上部设备重量5F1＝5 000 N，风载F3＝3 400 N；

（3）框架内部电缆、管接件F2＝820 N。

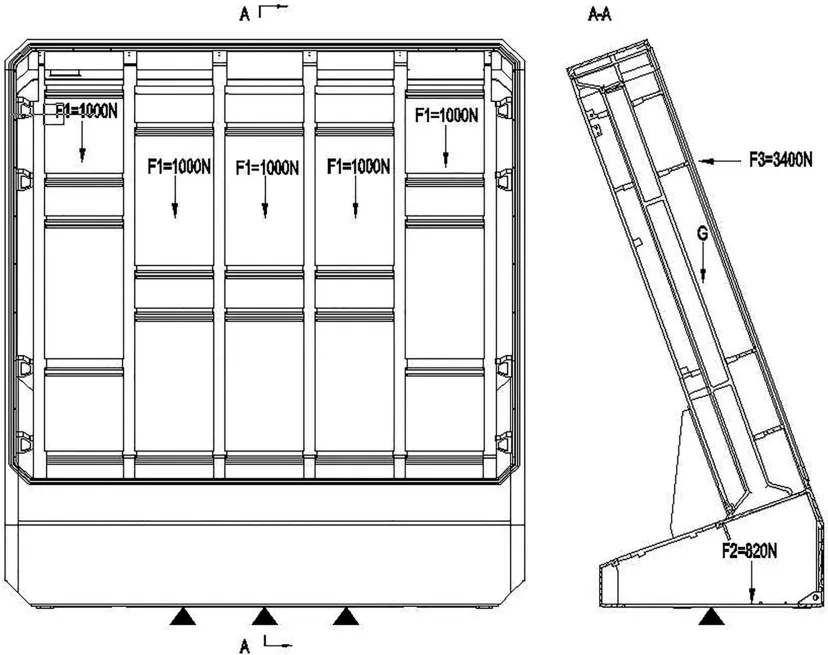
图1 某型雷达天线舱框架约束与加载图

2.4 静力、模态分析结果

经过Workbench静力求解计算得到强度分析结果。由应力云图和位移云图（图2）可以得到最大应力为114.2 MPa，最大位移为2.49 mm。

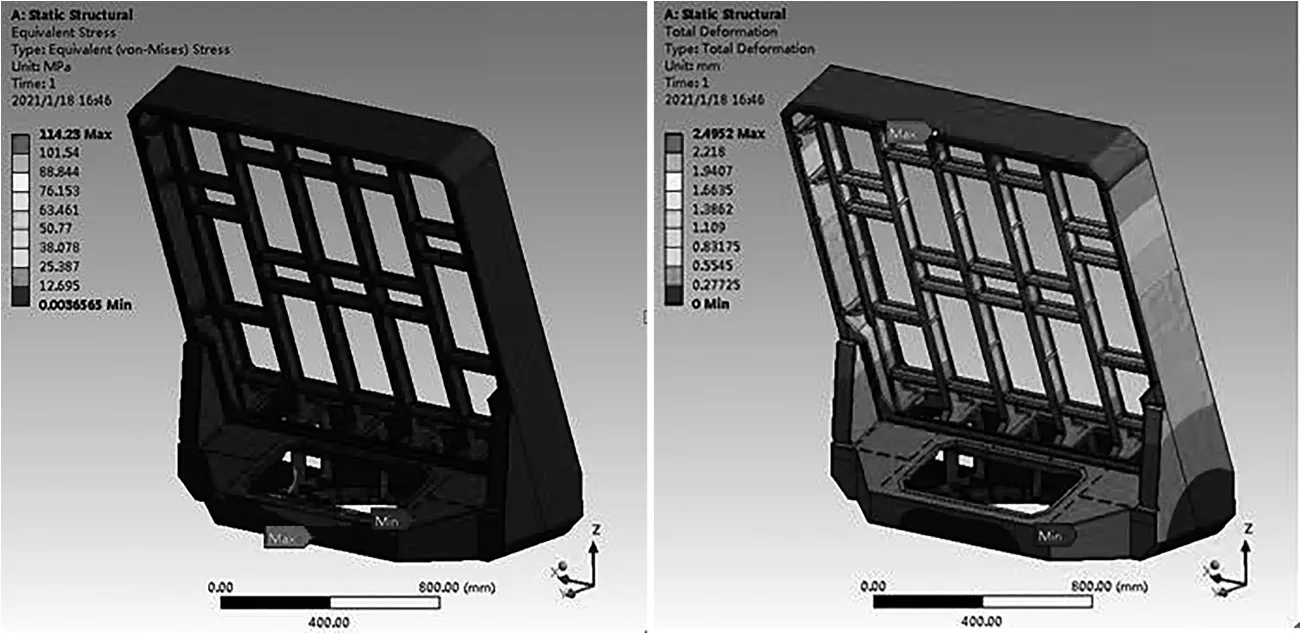
图2 天线舱框架应力与位移云图

经过Workbench模态求解器计算进行模态分析，可提取出模型的固有频率和模态振型。对基座施加约束，进行前6阶模态的分析计算，得到基座固有频率如表1所示。

表1 天线舱框架优化前固有频率

3 天线舱框架的拓扑优化设计

3.1 有限元拓扑优化求解

基于Workbench中的Shape Optimization模块对有限元模型进行拓扑优化。以单元材料密度为设计变量，体积减少百分比为约束函数，以结构的柔顺度最小化为目标函数。［2］

在Workbench中，导入模型后进行拓扑优化相关设置：首先进行模型约束设置，设置同静力分析一样；然后设置Shape Finder中的Target Reduction（质量减少目标函数）＝15%，进行运算求解，得出框架伪应力云图如图3，图中深色斑块区域位置表示经计算后在保证结构刚强度的前提下可去除的部分。

3.2 天线舱框架模型优化改进

如图3所示，可以优化的部分集中于框架前部、底部法兰、维修孔、加强筋以及安装组件的纵横梁处。结合整套设备的实际运行环境与受力情况，在三维设计软件NX中对原有结构进行规则切除与重塑［3］。如图4（a）所示，深色规则凹槽处为减重区域，同时在跨度较大的部位设置加强筋板，得出新的天线舱框架模型如图4（b）所示，与改进前模型相比，结构重量由140.6 kg下降为117.3 kg，结构减重16.5%。

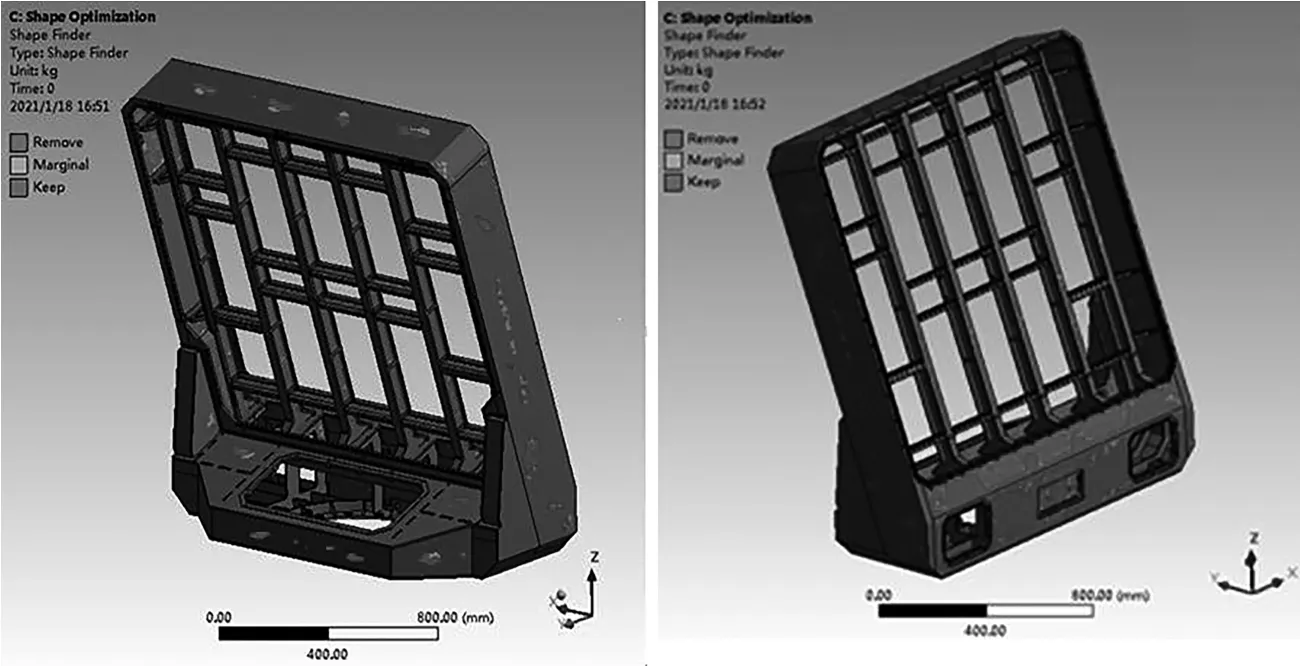
图3 天线舱框架伪应力云图

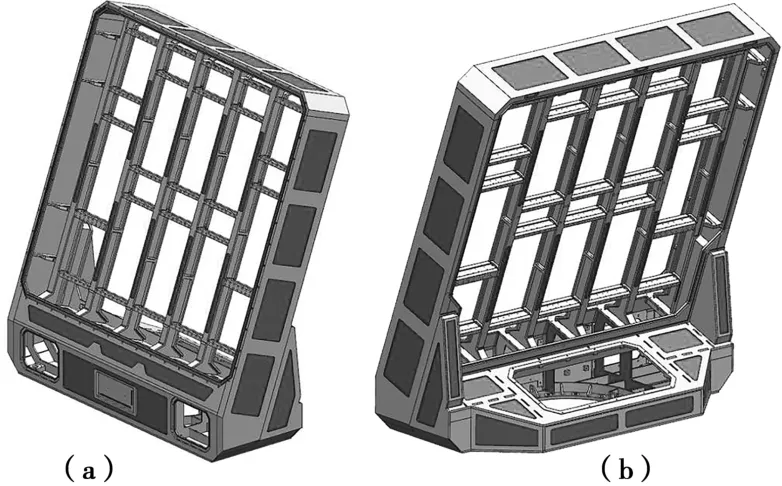
图4 改进后框架截面模型

3.3 优化后结构有限元分析

经过Workbench静力求解计算得到优化后静力学分析结果，由应力云图和位移云图（图5）可以得到最大应力为117.6 MPa，最大位移为2.94 mm。结构最大应力出现在框架底部与转台安装处，最大形变出现在面阵最上部，按照5A30铝合金材料的屈服强度275 MPa，安全系数1.5校核。因此，该框架在工作环境载荷激励下满足设计要求。改进前后模型的有限元分析结果见表2所示［4］。

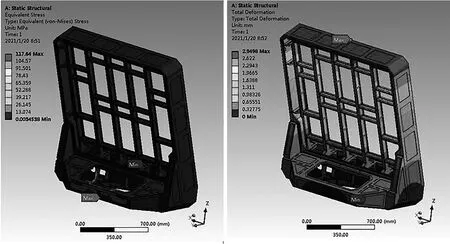
图5 优化后应力与位移云图

表2 框架优化前后静力学性能对比表

经过Workbench模态求解器计算进行模态分析，可提取出优化后模型的固有频率和模态振型［5］。对基座施加约束，进行前6阶模态的分析计算，得到天线舱框架优化前后固有频率对比如表3所示。

表3 框架优化前后模态对比表（单位：Hz）

4 结束语

本文使用三维设计软件NX与有限元分析软件联合对天线舱框架进行静力学和动力学分析，快速、有效地验证了结构设计对使用需求的满足性，极大地缩短了产品研制周期。通过有限元分析软件对天线舱框架结构进行拓扑优化设计，同时结合伪应力云图、边界条件改进框架构型，在三维设计软件NX中对原有结构进行规则切除与重塑，既保证了基座的刚强度和模态特性，又有效降低了设备质量（减重约16%），得到了较为优良的设计方案。有限元拓扑优化设计不仅为结构轻量化设计提供解决方法，同时对优化后的结构给予验证，进而大幅提高设计效率。拓扑分析方法也适用于其他大中型雷达的结构静、动力学仿真分析及轻量化设计。