磁场作用下倾斜方腔内纳米流体自然对流数值模拟
2021-06-17齐美娜罗小红
齐美娜,罗小红,陈 庆
(吉林化工学院 机电工程学院,吉林 吉林 132022)
随着纳米流体自然对流技术的广泛应用,如用于电子设备和动力电池等[1].纳米流体的热传导率也吸引了广大研究者对其进行深入研究.目前,关于纳米流体热传导率的研究主要集中在边界层问题、腔体形状及纳米颗粒的体积份额等.苏立功等人[2]研究了倾斜方腔内纳米流体的自然对流,他们得出结论,在方腔倾斜角度一定的情况下,换热速率随着Ra数增大而增大.王刚等人[3]在方腔一侧壁面温度按照正弦变化时,研究了CuO-水纳米流体的非稳态自然对流.研究结果表明考虑布朗运动比不考虑布朗运动时Nu数大.金翼等人[4]研究了TiO2纳米流体的对流换热系数,他们发现纳米流体的导热系数和对流换热系数是随纳米颗粒浓度的增大而提高的.Hussam等人[5]数值模拟了方腔内磁场对Al2O3纳米流体自然对流的影响,他们采用的参数为Ra(103≤Ra≤107)、纳米颗粒体积份额(0≤φ≤0.06)、Ha(0≤Ha≤60)、Pr=6.2.研究表明传热率随着Ra数的增大而增大.传热率随着Ha数的增大而减小.增大纳米颗粒体积份额可能导致传热率的升高或降低,主要取决于Ha数和Ra数.目前很多学者将纳米流体的研究方向集中在布朗运动对纳米流体以及纳米颗粒形状对传热的影响[6-11].很少有学者研究倾斜方腔并且施加与水平方向成γ角的磁场,不同纳米颗粒受Gr数和方腔倾斜角度的自然对流.
1 物理模型和数值模型
1.1 物理模型
该问题的物理模型,如图1所示.

图1 具有磁场的倾斜方腔的物理模型
倾斜方腔的左右壁面为恒温壁面,左壁面为高温壁面(Th),右壁面为低温壁面(Tc),上下壁面为绝热且为不渗透壁面.施加了与水平方向成γ角度的磁场强度为B0的稳恒磁场.方腔内充满为了以水为基液、分别为球形CuO、Al2O3、TiO2纳米颗粒的纳米流体(Pr=6.2),基液和CuO、Al2O3、TiO2纳米颗粒的热物性质参数,如表1所示[12-14].

表1 水和CuO,Al2O3,TiO2纳米颗粒的热物理性质
1.2 数学模型
本数值模拟中,做如下假设:
(1)纳米流体为各向同性、不可压缩、做层流运动的牛顿流体;
(2)因浮升力引起的纳米流体密度的变化采用Boussinesq假设;
(3)纳米颗粒和流体无相互滑动,纳米颗粒形状和纳米颗粒粒径分布均匀,纳米颗粒与基液处于热平衡状态;
(4)不考虑黏性耗散和hall效应;
(5)不考虑熵产的影响.
因此,对应物理模型的无量纲控制方程如下:
(1)
(2)

(3)
(4)
采用的无量纲变量如下:
(5)
式(5)的变量为:
其中,Gr为格拉晓夫数;Pr为普朗特数;Ha为哈特曼数;Nu为努塞尔数.
对应的无量纲边界条件为:
左壁面(X=0) ,U=V=0 ,Θ=1;
右壁面(X=1),U=V=0,Θ=0;
恒温壁面上局部的Nu数为:
(6a)
(6b)
无量纲流函数为:

(7)
在上述变量和部分方程中出现的下标f和nf分别代表水和纳米颗粒,本文中所采用的纳米属性应用模型,如表2所示.

表2 纳米流体属性应用的模型
2 网格独立解和数值验证
2.1 网格独立解
因为网格无关解是数值计算的基础,所以在数值模拟之前,先研究了网格无关解,相关数据如表3所示.
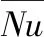
表3 不同Ha数下壁面上的数

2.2 数值验证
网格节点数为41×41,在采用Chebyshev配置点谱方法对磁场作用下倾斜方腔内纳米流体自然对流数值模拟之前,要先验证该文所采用算法的有效性.
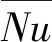

表4 不同体积份额下,壁面上的的对比
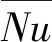
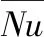
表5 在不同的纳米颗粒体积份额下,壁面上的的对比
3 结果与讨论
采用谱投影(IPS)[18]对控制方程进行时间上的离散,配置点谱方法对控制方程进行空间上离散,写成矩阵相乘[17]的形式,并用MATLAB软件编程求解.对倾斜方腔施加与水平方向成γ角度的稳恒磁场B0.数值模拟中的无量纲参数:普朗特数(Pr=6.2),纳米颗粒体积份额(φ=0.03),哈特曼数(Ha=30)保持不变.
如图2所示,Gr=2.0×105数保持不变,从左列温度场可以看出:方腔倾斜角度γ从0到π/4时,等温线中间部分由水平方向变为向下倾斜,说明此时的TiO2纳米流体传热加快;方腔倾斜角度从π/4到π/3时,中间段等温线变化不大.从右列的流场可以看到:方腔倾斜角度γ从0到π/4时,流函数绝对值由14变为24,流线由向上倾斜转为向下倾斜并形成两个涡.说明此时的流动加强;方腔倾斜角度从π/4到π/3时,流函数绝对值由24变为26,流线与竖直壁面平行.

(a)γ=0

(b) γ=π/4

(c) γ=π/3图2 Pr=6.2、Gr=2.0×105、φ=0.03、Ha=30时温度场(左侧)和流场(右侧)


表6 在Gr数和γ共同作用下,壁面上的
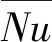

表7 不同纳米颗粒在不同的方腔倾斜角度作用下,壁面上的
4 结 论
本文采用Chebyshev配置点谱方法对磁场作用下倾斜方腔内纳米流体自然对流问题进行了数值模拟.在方腔的左右壁面分别给定恒温,方腔倾斜角度γ,不同纳米颗粒(TiO2、CuO和Al2O3),在Pr=6.2、φ=0.03、Ha=30的条件下,研究了方腔倾斜角度γ、Gr数对不同纳米流体自然对流的影响.研究结果如下:
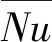
(2)纳米流体流动与传热受Gr数影响比较显著;
(3)不同纳米颗粒对传热影响趋势大致相同,Al2O3纳米流体的换热最好.
