西南电网异步联网后的负荷预测及频率波动抑制
2021-06-17罗卫华余锐兰强吴京驰王民昆肖嵩
罗卫华,余锐,兰强,吴京驰,王民昆,肖嵩
(1. 国家电网有限公司西南分部,四川 成都 610041;2. 西南交通大学电气工程学院,四川 成都 611756)
0 引言
电力系统负荷是电力系统稳定分析的重要指标之一,代表系统中所有用电设备瞬时消耗功率的总和。由于电力系统中电能储存量有限,发电量与负荷量需实时保持供需平衡。2014年12月29日,四川、重庆电网分别脱离华中电网与原西藏电网,组成了西南电网。2019年6月19日,随着渝鄂直流工程全部投运,西南电网与华中电网脱离交流同步互联,两大电网的交流输电线路全部断开。依靠背靠背直流输电工程,西南电网互联格局由交直流混联变为直流异步互联。电网的异步互联意味着两端电网旋转转动惯量相互分隔,各电网的频率稳定性能下降,增加了频率失稳风险。
西南电网异步互联工程启用以来,西南电网频率波动加剧,频率波动越过动作频率界限的情况频发,直流频率控制(frequency control,FC)装置动作频繁。电力系统有功瞬时不平衡将导致频率波动,由于西南电网的异步运行,有功不平衡对频率造成的影响将扩大,频率波动也随之加剧。因此,有效准确地预测有功出力及制定发电计划对频率偏差控制具有重大意义[1—4]。
随着现代人工智能技术的发展,机器学习方法被逐渐用于电力系统负荷预测[5—8],如经典时间序列预测法、人工神经网络方法、支持向量回归(support vector regression,SVR)等。其中时间序列预测法建模简单、预测速度快,但对于波动性大的负荷,预测精度较低。文献[9]采用双链马尔科夫方法预测负荷,达到了预期精度,但预测结果较为固定,无法跟随预测日的实际工况改变预测趋势。文献[10—11]使用长短期记忆网络(long short term memory,LSTM)进行负荷预测,该方法基于时间序列进行预测,未考虑多方面因素影响,故精度较低。人工神经网络预测精度高、优化潜力大,但存在一定问题,如收敛速度慢、难以确定网络结构和易陷入局部最优等。文献[11]使用反向传播(back propagation,BP)神经网络对某电力系统的负荷进行预测,考虑了气温对预测结果的影响,取得了一定效果。文献[12]所述的双层随机森林算法也取得了较好的效果。通常SVR算法只能进行单步预测,对于存在大量杂散干扰的数据,预测误差较大且预测效果滞后[13]。文献[14]使用基于气象综合因素指数和关联分析加权的最小二乘支持向量机(least squares support vector machine,LSSVM)算法,建立组合预测模型,气象综合指数仅表达了气象对人体的影响程度,无法客观反映气象对负荷的影响程度。
为提高负荷预测精度并弥补上述算法的缺陷,文中结合BP神经网络与SVR各自的优点,提出一种新型混合算法模型。使用预测精度较高的BP神经网络对系统负荷水平进行预测,使用不易陷入局部最优的SVR预测最终负荷值。其中,BP神经网络利用训练集的气象数据预测当日最大负荷,确定当日负荷水平。基于所得负荷水平,使用当日一段已知的负荷数据确定训练集权重并训练SVR模型,进而预测当日剩余时间的负荷曲线。该混合算法模型每隔一段时间根据最新的已知负荷重新训练模型,实现滚动预测,可适应突发工况。为了应对西南电网异步互联后的频率问题,使用BPA仿真将预测的负荷跟踪系统的有功出力,结果表明预测方法相较于未考虑负荷分布特性的传统预测方法,频率偏移抑制效果更佳。文中所提模型及方法对未来电网发电计划制定以及电力系统频率稳定性提升具有重要意义。
1 西南电网异步运行现存频率问题分析
西南电网异步运行后与西北、华中和华东电网之间的输电新格局如图1所示。异步运行的启动,意味着西南电网与华中电网的频率异步,依靠有功联络线输送功率。频率的变动规律与异步互联前有所变化。
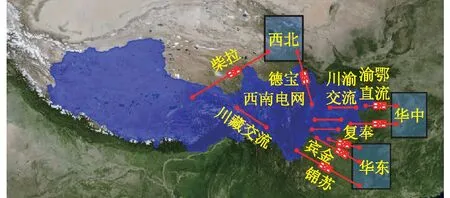
图1 西南电网与各大电网间的输电新格局Fig.1 New transmission pattern between Southwest Power Grid and other major power grids
西南电网异步运行前后相邻两周同一工作日的频率见图2。系统频率由相量测量单元(pha-sor measurement unit,PMU)测得。

图2 西南电网异步运行前后的系统量测频率Fig.2 Measured system frequency of Southwest Power Grid before and after asynchronous operation
西南电网异步运行前后,t-1到t+12共14 d的频率波动量超过±0.07 Hz,对期间直流FC动作次数进行统计,如表1所示。其中,t为异步运行启动当日,t-1为异步运行前一日,t+1为异步运行后一日,以此类推。

表1 直流FC动作次数Table 1 Action times of direct current FC
结合图2与表1可知,西南电网异步运行后,系统频率较异步运行前波动加剧,直流FC动作较为频繁。
结合数据与转子运动方程的理论分析可知,西南电网异步运行后系统的总惯量下降。当系统有功功率与负荷不匹配时,频率波动幅度加剧。因此,负荷预测可以预先把控有功平衡、提前制定发电计划、实施自动发电控制(automatic generation control,AGC)超前控制等,从负荷端抑制频率波动。
西南电网异步运行前后共14 d的负荷曲线见图3。图中,14 d的最大、最小负荷分别为47 422 MW,27 840 MW。由图3可知,西南电网的负荷呈周期性,负荷变化特征受异步互联影响有限。异步互联工程的启用通常对负荷影响很小,电力负荷具有明显的日周期特性。负荷存在极大值和极小值点,在极大值点,每日的负荷变化趋势总体一致。但由于每日的负荷受生活习惯、气象等因素影响,相同时间点的实时负荷存在一定差值。

图3 西南电网异步运行前后14 d的负荷曲线Fig.3 14-day load curve before and after asyn- chronous operation of Southwest Power Grid
西南地区分别以1 s,1 min为时间尺度的负荷波动幅值概率分布如图4所示。可以看出,1 s时间尺度下,负荷波动范围限制在100 MW以内,波动大于60 MW的概率不足1%,波动比较平缓。1 min时间尺度下,负荷波动主要集中在200 MW以内,波动变化在200 MW以上的概率不足1%。文中将秒级与分钟级的负荷波动概率纳入负荷预测过程,提高负荷预测精度。

图4 西南地区负荷波动幅值概率分布Fig.4 Probability distribution of load fluctuation amplitude in Southwest China
2 预测算法原理
根据西南电网负荷特点,文中提出一种新型混合算法对负荷进行预测。该算法在BP神经网络预测日负荷水平的基础上,使用SVR算法预测负荷曲线,并将待预测日已知的一段负荷数据与历史相同时间节点的负荷数据进行比较,调整训练集的权重。根据历史数据的负荷波动幅值概率分布修正预测结果,提高模型预测精度及可靠性。
2.1 SVR原理
SVR算法分为ε-SVR模型和v-SVR模型[15]。ε-SVR模型的初始参数优化较为困难,v-SVR模型使用改进网格搜索算法可以得到较好的初始参数[16],文中所述SVR算法采用v-SVR模型。
对于训练数据x=[x1,x2,…,xi,…,xn],对应的训练目标为y,二者之间存在从特征集到目标集的映射关系f,即求解目标函数f(x) =wΦ(x) +b。其中Φ(x)为非线性函数;w,b为权值矩阵和对应偏置。SVR可训练f(x)的风险函数最小化,即最大化分隔超平面。SVR训练过程如图5所示。

图5 SVR模型训练原理Fig.5 Training principle of SVR model
风险函数可表示为:
(1)
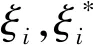
约束条件为:
(2)
式中:ε为线性不敏感损失函数。
构建拉格朗日函数为:
(3)

考虑Karush Kuhn Tucker(KKT)边界条件和对偶问题,最优对偶变量和约束的乘积为0。
(4)
线性函数逼近式可表示为:
(5)
式中:K(x,xi)为SVR的核函数;b可由式(5)求得。
核函数通常分为4类。
(1) 线性核函数。
K(hi,hj)=〈hi·hj〉
(6)
式中:hi,hj为样本集向量;〈hi·hj〉为hi和hj的内积。
(2) 多项式核函数。
K(hi,hj)=(〈hi·hj〉+1)d
(7)
式中:d为多项式的次数。
(3) 径向基核函数。
K(hi,hj)=e-‖hi-hj‖2/(2σ2)
(8)
式中:σ为径向基核函数的带宽。
(4) Sigmoid核函数。
K(hi,hj)=tanh(a〈hi,hj〉+c)
(9)
式中:tanh(·)为双曲正切函数;a,c为相关参数。
2.2 基于相关影响因素的最大负荷值预测
文献[17—20]指出,电力系统的负荷与负荷日的类型相关。考虑天气及是否工作日等因素,针对每日预测的最大负荷值,选取相关特征如表2所示。

表2 影响负荷的相关特征Table 2 Related features affecting load
上述每个相关特征都对应BP神经网络的特征,将每个参数归一化处理后,输入BP神经网络进行训练。对于西南地区,每个小地区同一日的气候数据通常不同。收集到的气象数据仅代表局部区域特点,不能很好地反映整个区域的气象水平。针对西南大区域的负荷预测,采集到每个小区域的气象数据后,大区域的总体气象特征可以表示为:
(10)
式中:xij为小区域j中特征量i的气象特征;Sj为小区域j的面积;N为区域数量。
针对该类型问题,通常使用神经网络方法进行预测。神经网络具有反馈调节网络权值的能力,对于非线性回归问题有较好的预测效果。基于表2中的特征,以每日最大负荷为目标训练BP神经网络,然后对目标进行预测。BP神经网络训练结构示意如图6所示。

图6 BP神经网络训练结构Fig.6 Training structure of BP neural network
训练神经网络可使特征量以各自的权重表达当日最大负荷值,使预测值与实际值的误差在训练集基础上达到总体最小。模型训练完成后可以根据待预测日的天气预测最大负荷值,为后续模型的准确预测提供基础。
2.3 新型混合算法
负荷量通常会根据工作日、休息日、节假日等特殊日期发生相应变化。目前已有研究将该类特殊日期作为特征值对模型进行训练[3,21]。同类型日期的负荷数据通常具有较高的重复度,不同类型日期的负荷数据通常差异较大。
实际电网运行中,特征值的选择不限于表2,还可能存在国民经济提升、产业结构改变、自然天气突变等不可预知因素。这些因素特征不稳定且提取困难。文中提出一种新型混合算法,将SVR算法和BP神经网络算法相结合。基于气象数据采用BP神经网络预测负荷水平,利用所得负荷水平作为SVR算法训练集的选取依据。从历史数据中选取接近该日预测负荷最大值的数据作为SVR的训练集。模型训练过程中使用搜索网格算法优化SVR的参数与核函数。获得混合算法模型的预测结果后,通过西南地区历史负荷波动幅值概率分布修正SVR结果并滚动更新负荷预测结果,使预测结果能更适应西南地区的负荷特点。具体模型训练流程如图7所示。

图7 新型混合算法模型训练流程Fig.7 Training process of novel hybrid algorithm model
SVR模型的训练从训练集选取待预测日已知的一段时间负荷数据作为测试样本的特征集,用于输入模型预测整日的负荷曲线。训练集的选取通过历史日负荷峰值与当日预测峰值的差异调整训练集的权重,差异较小的权重大,差异较大的权重小。目标集选取剩下时间段待预测的负荷。将当日已知一段时间的负荷测试样本输入模型,预测当日剩余时间的负荷。并随着时间推移,对当日负荷进行滚动预测。训练SVR的数据划分方式见图8。

图8 训练SVR的数据具体划分方式Fig.8 The specific division of data for training SVR
2.4 误差评价标准
误差评价标准是用于比较预测值与实际值之间误差的指标。用平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)表示短期负荷Pl的预测误差。MAPE用来衡量预测值与实际值之间的相对误差大小,RMSE用来衡量预测值与实际值之间误差的离散程度。
(11)
(12)
式中:M为误差评价的样本数;Pl,pre,Pl,real分别为负荷预测值和实际值。
3 负荷预测算例
算例选取西南区域电网异步运行后一个月的历史负荷作为新型混合算法模型的训练集数据库,同时采集对应时间段的相关气象数据作为特征预测当日最大负荷值。
3.1 工作日负荷预测结果分析
此次预测选择周一至周五任意工作日作为测试样本。将已知待预测日负荷的前30 min数据作为测试样本的特征集,后23.5 h的数据作为测试样本的目标集。采用图7的训练流程,模型训练完成后,使用测试集进行检验。使用新型混合算法所得的第1次负荷预测结果及绝对误差(预测值与实际值之差的绝对值)如图9所示。

图9 工作日第1次预测结果及绝对误差Fig.9 The first forecasting result and absolute error on weekdays
第1次负荷预测的eMAPE为0.940 9%,eRMSE为348.46 MW。预测间隔选取30 min,该日一共进行47次滚动预测,从当日00:30开始,每次时间步进30 min,将实时获得的每30 min负荷数据作为SVR的特征集,进而预测后续负荷,每次预测误差如图10所示。
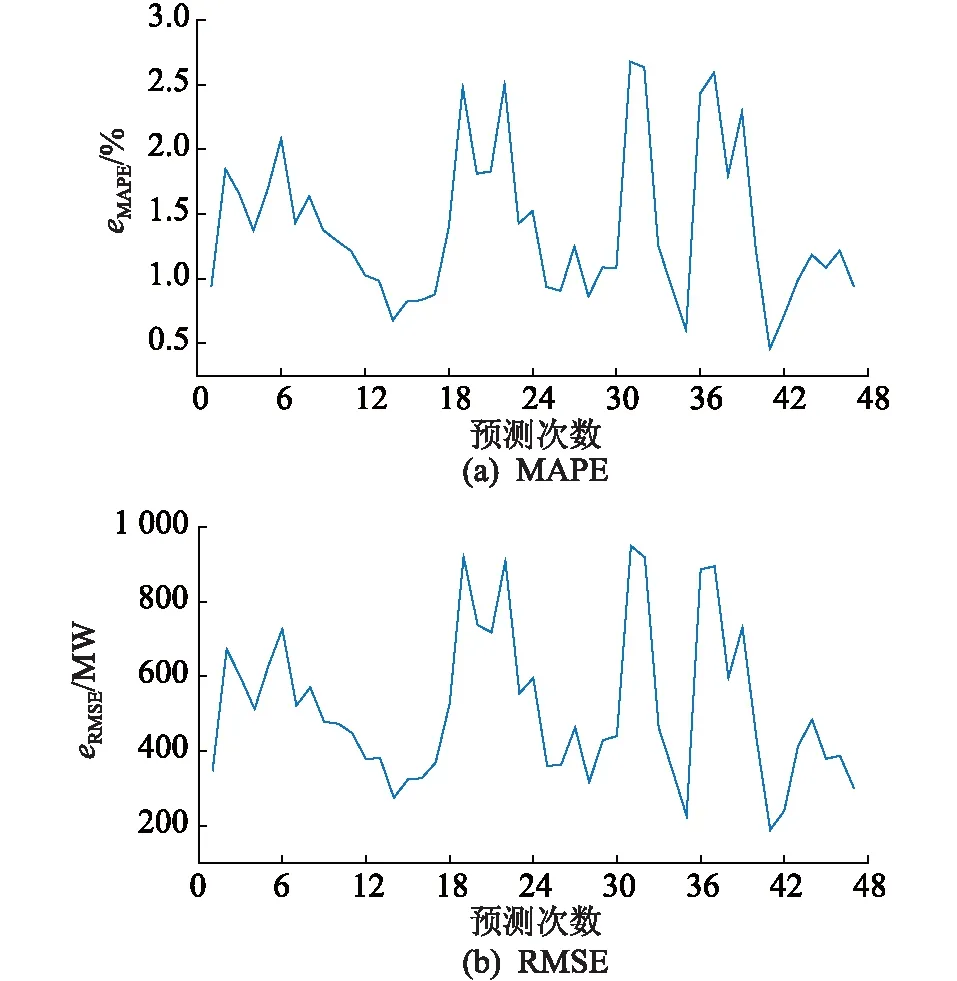
图10 工作日负荷预测误差Fig.10 Load forecasting error on weekdays
由图10可知,工作日负荷预测eMAPE均处于2.7%以下,eMAPE的平均值为1.401 2%,eRMSE均处于950 MW以下。
3.2 休息日负荷预测结果分析
与工作日预测方法相似,休息日同样选取30 min作为模型更新步长,第1次预测将前30 min作为测试样本特征集,后23.5 h为目标集。第1次预测结果如图11所示。

图11 休息日第1次预测结果及绝对误差Fig.11 The first forecasting result and absolute error on weekends
由图11可知,当对休息日进行预测时,混合模型对前半日的预测较为准确,后半日预测误差较大。随着待预测日时间的推移,模型将进行多次预测,每次步长30 min,当进行第27次预测时,模型受实时负荷影响,不断修正预测结果,如图12所示。
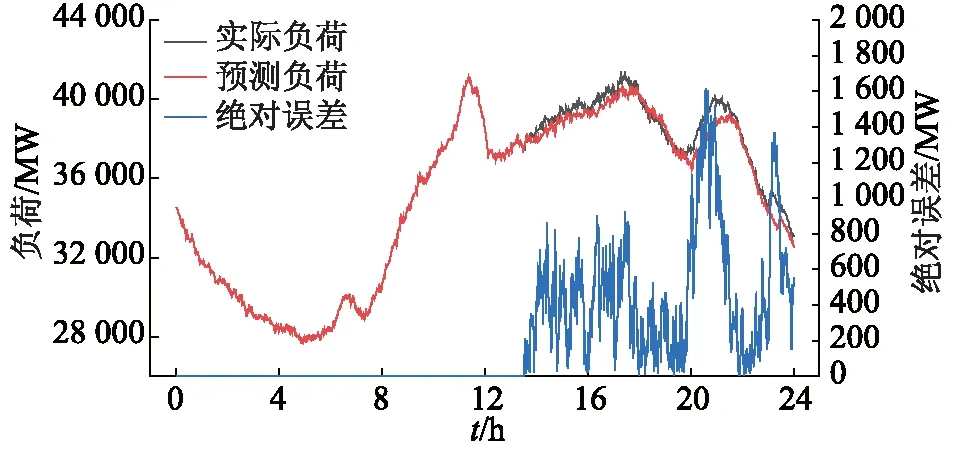
图12 休息日第27次预测结果及绝对误差Fig.12 The 27th forecasting result and absolute error on weekends
随着预测日当天时间的推移,不断会有当天的实际负荷数据生成,这些数据比历史数据更有意义。每隔30 min,模型将最近30 min的实时负荷数据作为模型的输入,预测当日的后续负荷。当突发事件发生时,模型会根据实时数据滚动更新后续预测结果。该新型混合预测算法选定的时间步长为30 min,每经过30 min,训练模型会抛弃预测当天相对久远的数据,使用新数据作为SVR测试集特征,回归预测当日剩余时间的负荷,每日一共滚动预测47次。使用此方法可以一定程度减小随机事件造成的误差。预测日共47次预测误差如图13所示。
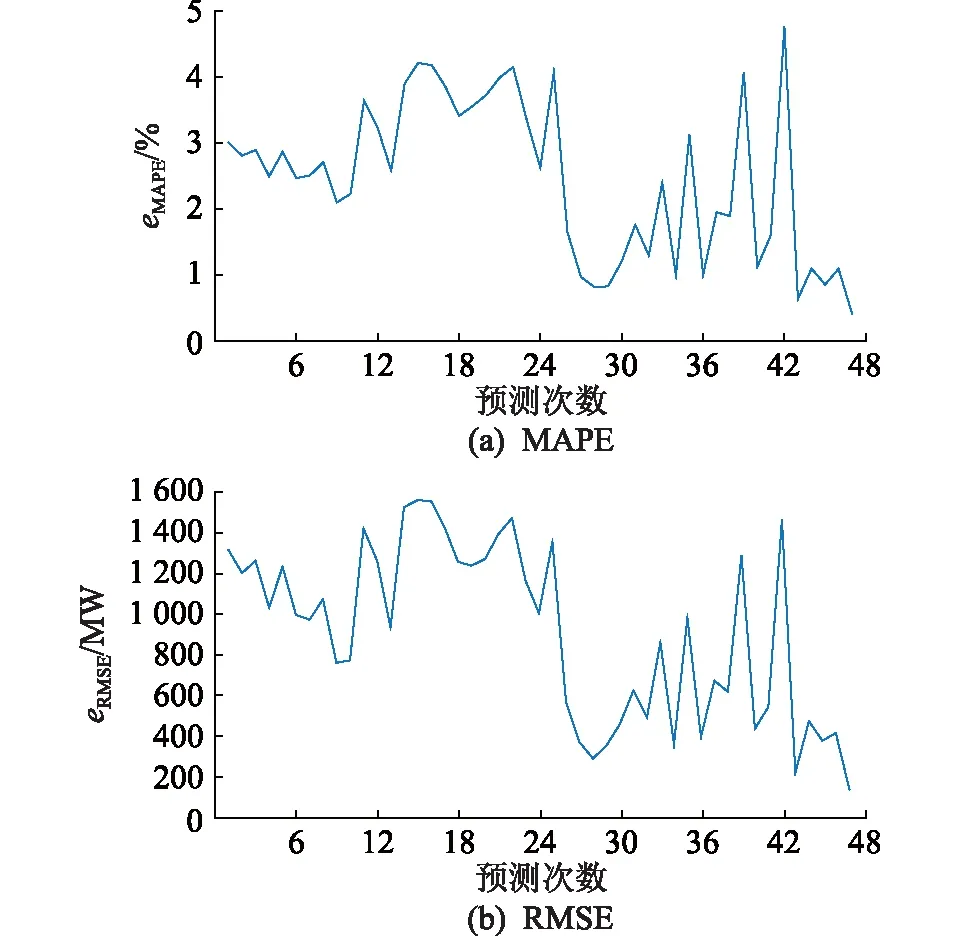
图13 休息日负荷预测误差Fig.13 Load forecasting error on weekends
由图13可知,当待预测日为休息日时,使用模型进行第1次预测,结果显示该日后半段负荷预测误差较大。经过27次预测后,实际负荷参与混合模型训练,可对预测结果进行调整。待预测日的后半段预测结果与实际负荷误差减小,预测精度提升。从第27次预测开始,eMAPE和eRMSE减小,可见实时负荷数据的更新可对模型进行修正。
3.3 负荷预测误差比较
为体现BP神经网络对负荷预测结果的影响,基于预测和实际负荷分别对模型进行训练,14 d的eMAPE平均值分别为1.67%,1.55%。可见,BP神经网络的预测精度与实际情况的误差较小,即精度较高。
使用文中所提新型混合算法与文献[10—11]所述的LSTM、文献[22]所述的双层随机森林算法进行比较,eMAPE结果如表3所示。

表3 3种机器学习方法的eMAPE比较Table 3 eMAPE comparison of three machine learning methods %
4 基于负荷预测结果的频率仿真
为验证负荷预测结果对西南电网的频率控制效果,基于几种机器学习方法的负荷预测结果,利用BPA仿真软件对负荷波动下的西南电网频率响应进行仿真。仿真模型基于西南异步后的系统,选取真实系统平衡运行时某一时刻的潮流作为潮流仿真数据,选取该时间节点后15 min的负荷数据进行频率响应仿真。实际及预测负荷如图14所示,图中选取与文中预测精度更接近的双层随机森林算法进行比较。

图14 实际负荷及两种算法的负荷预测结果Fig.14 Actual load and load forecasting results of two algorithms
仿真过程中,设置负荷波动为:
ΔPL(i)=PL(i+1)-PL(i)
(13)
式中:PL(i)为当前时刻的实际负荷;PL(i+1)为下一仿真时刻的实际负荷;ΔPL(i)为仿真设置的负荷变化量。
根据算法预测结果,可提前安排有功功率。设置系统有功增量为:
ΔPG(i)=PG(i+1)-PG(i)
(14)
式中:PG(i)为当前时刻的系统有功发出值;PG(i+1)为下一仿真时刻的负荷预测值;ΔPG(i)为仿真设置的有功变化量。
仿真基于实际西南电网简化后的模型,包括282台发电机,1 825条母线。模型考虑了发电机的励磁系统、系统稳定器、调速器等数学模型。设置仿真步长为0.01 s,总时长为900 s,负荷类型为40%恒功率负荷及60%恒阻抗负荷。负荷每隔6 s产生一次扰动,负荷扰动曲线如图15所示。

图15 负荷扰动曲线Fig.15 Load disturbance curve
作为典型含高比例水电的电网,西南电网水电装机总容量突破8 000万kW,水电容量占比70%以上,频率稳定需要网内机组一次调频与AGC相互配合动作。调频主要依靠水电机组完成,由于水电机组水锤效应,初始功率变化与导叶开度变化相反,造成水轮机环节相位滞后,高比例水电系统调频过程中小干扰稳定问题突出。大型水电机组的AGC信号传输延迟大约20 s,AGC控制调节到位的时间则需按照爬坡速率折算(1 min可调整装机容量的15%~20%,即8 000 MW/min)。由图15可知,15 min内的负荷波动在200 MW以内,故AGC控制在2 s内自动调用发电机旋转备用容量。算例负荷数据选取该时间节点后15 min的负荷进行仿真,西南电网各电站可根据30 s时段负荷预测结果调整发电出力。故在15 min内,AGC控制可根据负荷预测结果实时调整发电计划约30次。对西南电网一次调频下该段负荷的频率响应进行仿真,不同负荷预测算法的频率响应结果如图16所示。

图16 不同算法预测的西南电网一次调频频率波动Fig.16 Frequency fluctuation of primary frequency modulation in Southwest Power Grid predicted by different algorithms
由图16可知,在一次调频作用下,相对未采用负荷预测算法(实际的频率波动)而言,根据负荷预测结果制定的发电计划可极大抑制频率波动最大值,且在电网一次调频作用下,系统频率波动有所减缓。采用文中新型混合算法、双层随机森林算法、未采用负荷预测算法的频率响应eRMSE分别为0.022 7 Hz,0.026 0 Hz,0.037 1 Hz。相较双层随机森林算法的预测结果,使用文中提出的新型混合算法的预测结果对系统进行一次调频,频率波动更小。
5 结语
西南电网异步运行后,有功不平衡导致频率问题突出、直流FC装置动作频繁。为解决有功不平衡导致的频率问题,文中提出了采用组合BP神经网络和SVR算法的新型混合算法用于电力系统负荷预测。基于气象数据、电力系统历史数据以及预测日当天已有数据,采用BP神经网络对当日最大负荷进行预测,从历史数据选择与最大负荷最相近的训练样本建立模型。采用当日一段已知数据作为SVR模型的输入,结合BP神经网络划分的训练集训练模型,预测当日剩余时间的负荷。误差分析结果表明,新型混合算法所得结果满足负荷预测需求。同时,基于新型混合算法所得负荷预测结果制定的发电计划对频率控制有着积极作用,可极大改善系统频率偏移与波动程度。
下一步可从如下方面开展研究:基于丰富的历史数据库建立考虑多特征的预测模型;优化预测模型结构、核心算法等,如选择预测精度更高的人工智能网络。旨在进一步提高电力系统负荷预测精度,有效制定发电计划,抑制电网频率波动。
