双最小二乘支持向量数据描述

张仙伟，邢佳瑶

(西安石油大学 计算机学院，陕西 西安 710065)

0 引 言

TAX提出支持向量数据描述(support vector data description，SVDD)[1]算法，在单值分类领域得到了广泛应用。陆从德将SVDD推广至分类领域，根据数据的描述边界进行分类并采用乘性规则求解[2]。从提高SVDD求解速度入手，ZHAO F等构造一种简化算法，寻求特征空间中支持向量的基函数以提高测试速度[3]。LAN J C将SVDD算法拓宽应用于在模拟电路，并通过独立成分分析进行特征选择以提高训练速度[4]。NIAZMARDI S等利用SVDD改进模糊C均值聚类算法，并用于无监督高光谱数据分类[5]。PENG X J等设计避免矩阵求逆的运算方法，提高传统SVDD的分类精度[6]。刘富等从提高分类精度角度，设计根据位置分布构造可变惩罚参数的方法[7]。CAO J等拓宽SVDD用于癌症多分类的快速基因选择方法[8]。REKHA A G等根据SVDD目标函数的梯度下降方向找到球心的近似原像，避免了拉格朗日乘子的计算问题并降低了复杂度[9]。陶新民等设计密度敏感最大间隔SVDD算法，根据样本在空间的分布，解决不均衡的数据分类问题[10]。GUO Y等将SVDD与多核学习结合构造多分类器[11]。引入集成学习理念，Pranjal利用斜二叉树和SVDD构造改进的多分类算法[12]。GORNITZ N进一步应用集成学习思想[13]，利用SVDD和K均值聚类构造单值分类算法。YIN L L等将SVDD应用于奇异值检测，构造具有较好鲁棒性的积极学习算法[14]。在无线传感器网络领域，HUAN Z等设计SVDD算法进行奇异值检测[15]，而SHI P等在此基础上设计改进的SVDD算法[16]。陶新民等针对故障检测设计一种不均衡的最大间隔SVDD模型[17]。WANG K Z等设计针对污染数据的鲁棒支持向量域描述算法[18]。为了进一步提高SVDD的训练速度和降低计算复杂度，ZHANG L等利用超球球心和半径之比选择特征[19]。ZHENG S F修改SVDD模型的拉格朗日函数为可微凸函数，并设计一种迭代算法求解，更加快速有效且分类精度较高[20]。高罗莹等在室内无线局域网中引入SVDD算法[21]，解决了已有检测技术的适应性较差和检测性能较低的问题。吕国俊等学者结合蚁群优化算法进行相似重复记录检测[22]。这些研究取得了一定的进展，拓宽了SVDD的应用领域，或提高SVDD的分类精度，或降低SVDD的复杂度，或增加SVDD的鲁棒性。然而，设计过程中往往需要借助其余算法，例如独立成分分析、多核学习、K均值聚类、粒子群优化等，计算较为复杂。

如果构造出既能够缩短运行时间、提高可处理问题的规模，又能够保证较高的分类精度的分类算法，则能有效提高算法在各个领域的运算效率。最小二乘支持向量机将标准算法的不等式约束改为等式约束，具有计算简单、分类精度高的优点[23]；对SVDD进行分片[24]和对SVM进行分区域处理[25]的思想，有效提高了相应算法的分类精度。笔者受最小二乘思想和分块处理思想的启发，构造双最小二乘支持向量数据描述DLSSVDD；将支持向量数据描述中的不等式约束修改为等式约束，同时结合样本到2个最小包围超球的距离设计分区域的分类准则。DLSSVDD仅需求解一个线性方程组而非凸二次规划，训练仅对一类样本进行且考虑样本在空间的位置分布；预计DLSSVDD具有较低复杂度、较短的分类时间、较高的分类精度。

1 双最小二乘支持向量数据描述

简要给出最小二乘支持向量机和支持向量数据描述的工作原理。

1.1 最小二乘支持向量机

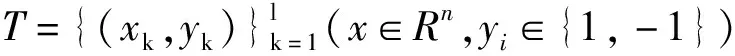
s.t.yi[w·φ(xi)+b]=1-ξi,i=1,…,l

(1)

以拉格朗日乘子αi≥0乘以每个等式约束，加入优化目标得到拉格朗日函数L。

(2)

根据KKT最优解条件，置L对变量w,ξi,b,αi的偏导为零，得到的最优解条件可以表述为如下线性方程组

(3)

这里Ωij=yiyjk(xi,xj)，I为单位矩阵；k(xi,xj)=φ(xi)Tφ(xj)为核函数，y=[y1,…,yl]T,e=[1,…,1]T。

根据线性方程组(3)的解α和b，构造分类判别函数

(4)

1.2 支持向量数据描述

记{xi}(i=1,…,N)为n维空间Rn中的目标类样本，SVDD求取一个半径最小的超球来覆盖全体目标类样本。由于样本并非总是球形分布，SVDD通过非线性映射φ∶x→φ(x)将样本投影到一个高维的特征空间。SVDD对样本xi引入松弛变量ξi>0以放松约束条件，并引入正比于违反约束总量的惩罚参数C>0。记最小包围超球的半径和球心分别为R和a，SVDD在非线性空间中求解如下凸二次规划

s.t.(φ(xi)-a)T(φ(xi)-a)≤R2+ξi,

ξi≥0,i=1,…,N

(5)

SVDD采用Lagrange乘子法，求解(5)的对偶规划得到原问题的解

(6)

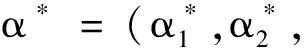
最小包围超球的球心按照下式进行计算

(7)

最小包围超球半径根据下式计算

(8)

如果待测样本z到最小包围超球球心的距离平方小于超球半径R2，接受该测试样本为目标类；否则，拒绝该样本，将其作为非目标类。

‖φ(z)-a‖2≤R2⟹

(9)

1.3 双最小二乘支持向量数据描述

s.t.[φ(xi)-a+]T[φ(xi)-a+]=[R+]2+ξi,ξi≥0,i=1,…,N

(10)

这里R+(R-)和a+(a-)为正(负)类样本最小包围超球S1(S2)的半径和球心；ξi为样本xi的松弛。

构造上述规划的拉格朗日函数

(11)

这里R+和a+为正类样本最小包围超球S1的半径和球心；ξi为样本xi的松弛。

对上述拉格朗日函数关于所含变量求导，并置变量的偏导数为零，得到

(12)

将所得等式带入目标函数，得到如下问题

(13)

这里α=[α1,α2,L,αN]T，IN是N×N阶的单位阵;K=[k(x1,x1),k(x1,x2),…,k(xN,xN)]为核矩阵，K(xp，xq)=φ(xp)·φ(xq)为核函数。

KKT最优性条件整理为

(14)

式中Φ为对核矩阵K进行正交分解所得矩阵，也即非线性映射矩阵。

根据式(14)求得的最优解，得到正类样本的最小包围超球半径的计算公式

(15)

给定测试样本z，其与超球球心的距离按照如下2式计算。

d1=D(z,S1)=‖φ(z)-a+‖2

(16)

d2=D(z,S2)=‖φ(z)-a-‖2

(17)

给定待测样本z，双最小二乘支持向量数据描述以如下函数作为分类决策函数

(18)

式中R1=R+，R2=R-,S1=(R+,a+)为正类样本的最小包围超球；S2=(R-,a-)为负类样本的最小包围超球。

2 数值试验

为验证DLSSVDD的性能，选取不同规模的基准数据集和正态分布数据集进行实验。所有实验均在P4CPU，3.06 GHz，内存为0.99 GB的PC机上进行；所有程序均采用Matlab 7.01编写。

例1 正态分布数据集

在二维空间中，调用Matlab中的mvnrnd 函数生成满足正态分布的正类和负类样本各250个。正负类样本的均值分别取为μ1=[0.4,0.8]和μ2=[0.8,0.4]，协方差矩阵均取为单位矩阵；数据集利用r=mvnrnd(mu，SIGMA，250)生成，其中mu为均值，SIGMA为协方差矩阵，250为样本总数。

为了验证DLSSVDD的分类精度，选取径向基核函数K(x,y)=exp(-‖x-y‖2/σ2)进行数值实验，取径向基核参数σ=0.5，并取惩罚参数为C=1。视正类样本作为目标类(Target)，其余样本作为奇异值类(Outlier)。图1给出了样本集的分布，以及算法DLSSVDD对目标类和奇异值类的分类精度。

图1 DLSSVDD的分类精度

例2 Diabetics数据集

Diabetics为含有768个样本的8维数据集。随机选取468个样本参与训练，其余300个参与测试。为避免随机性，进行10次随机抽取实验，并列出训练集和测试集上的平均结果。

实验选取径向基核函数，惩罚参数取为C=1；随着径向基核参数的变化，以分类精度和运行时间作为评价指标，对比DLSSVDD和SVDD的分类表现，并列出相应结果见表1。

从表1可以看出，对于不同的核参数取值，DLSSVDD的分类精度和分类时间均比SVDD要低。同时可以看到，当核宽参数从σ=0.1增加到σ=0.5时，2种算法的分类精度均随核参数的增加而降低，只是变化幅度不同；SVDD分类精度的变化幅度约为5.6%；而DLSSVDD分类精度的变化幅度约为2.3%。

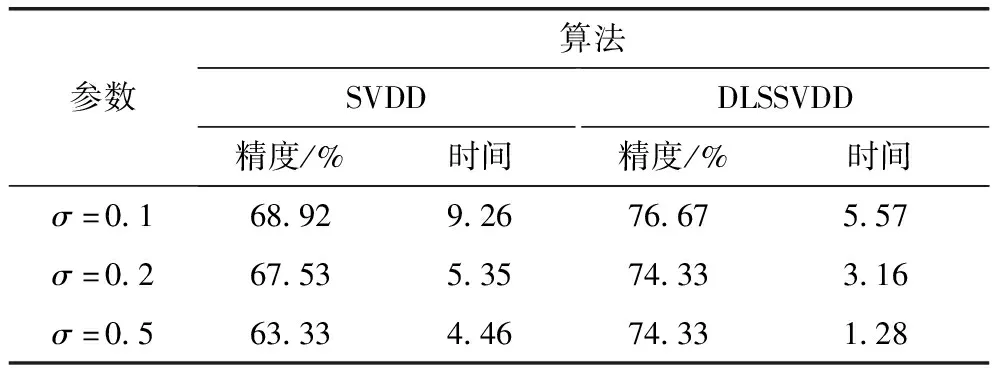
表1 DLSSVDD和SVDD的比较

例2 Breast Cancer和Banana数据集

另取UCI数据集中的Breast Cancer和Banana数据集进行测试。前者为包含277个样本的9维数据集，随机选取200个参与训练，其余77个参与测试。后者为包含5 300个样本的2维数据集，随机抽取400个样本参与训练，其余参与测试。

为便于比较，对不同算法设置相同的参数，均取径向基核函数，取惩罚参数为C=1，核宽参数为σ=0.1；列出不同算法在训练集和测试集上的平均分类精度和分类时间见表2，并将最优分类结果加黑表出。

表2 不同算法的表现

由表2看出，DLSSVDD在不同的数据集上均具有最高的分类精度和最短的分类时间。由于Banana数据集的测试集规模较大，在其上的分类精度可以代表算法的泛化能力；不妨以Banana数据集为例展开分析。DLSSVDD的分类精度分别比SVM、LSSVM和SVDD高1.76%，2.64%和0.22%；而分类时间依次是三者的16.51%，49.30%和77.43%。显见，DLSSVDD对训练精度提高的幅度较低，在分类时间上具有著优势。

例3 大规模数据集

本例依旧调用Matlab中的Mvnrnd 函数生成满足正态分布的二维空间数据集，并保持正类和负类样本的的数据均等。为了验证算法在大规模数据集上的分类表现，依次增加正类和负类样本的数目，并随机交换部分样本的正负号，使得有5%的重合。正类和负类样本的均值分别取为μ1=[0.2,0.6]和μ2=[0.6,0.2]，协方差矩阵依旧取单位矩阵，正态分布数据集的规模为2 000，4 000，8 000和10 000。

随机选取50%的样本参与训练，其余参与测试；取10次随机抽取实验的平均结果。设置惩罚参数C=1，取径向基核函数并取核宽参数σ=1；表2对比给出不同算法的分类性能。

由表3显见：DLSSVDD的分类精度与SVDD的相当，而分类时间远远低于SVDD的分类时间；同时这种分类精度和分类时间上的优势在样本规模较大时，也即参与训练的样本集数目较多时，体现的更为明显。

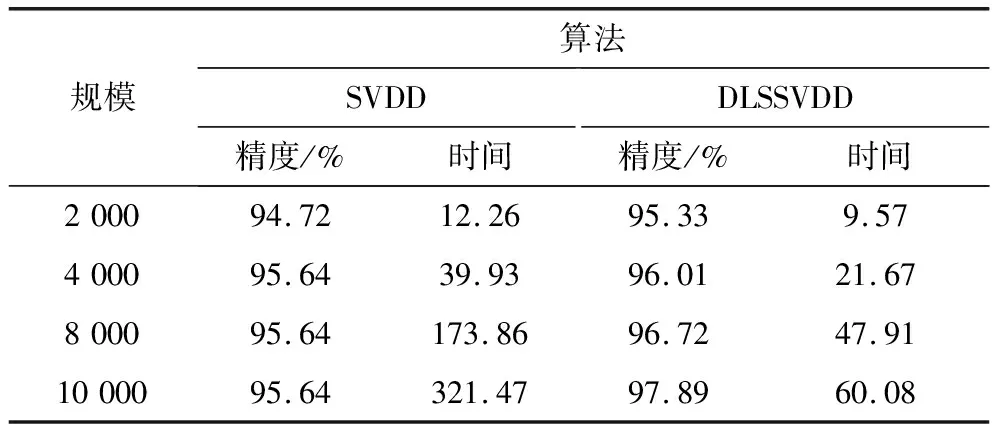
表3 SVDD与DLSSVDD的分类性能

以2 000个数据集为例，DLSSVDD的分类时间9.57 s是SVDD分类时间12.26 s的78.06%；当样本数目增加到10 000时，DLSSVDD的分类时间60.08 s是后者12.26 s的18.69%。

3 结 论

1)DLSSVDD具有比SVDD更短的分类时间。DLSSVDD在分类时间上具有明显优势，一方面是因为DLSSVDD减少了参与训练的样本规模，仅需带入单一类别的样本进行训练，而不需要像SVDD那样带入全体样本参与训练；另一方面是因为DLSSVDD将支持向量数据描述中的不等式约束改为等式约束，采用类似最小二乘支持向量机的思想，通过求解一个线性方程组得到最优解。

2)DLSSVDD具有比SVDD略高的分类精度。这是因为DLSSVDD同时考虑了正类样本和负类样本，根据待测样本与2个最小包围超球修心的距离，通过一个分段函数来判断类别标签。这样更符合样本的空间分布。

3)与SVDD相比，DLSSVDD分类时间方面的优势在大规模样本集上体现的更为明显。以正态分布数据集上的数值实验为例，DLSSVDD保持了较高的分类精度，而分类时间随样本规模的变化而增加的幅度并不明显。这得益于DLSSVDD仅通过求解一个线性方程组得到最优解，而避免了传统SVDD算法对凸二次规划的求解。鉴于DLSSVDD在这3个方面的优势，下一步研究方向将拓宽DLSSVDD在大规模样本集的分类问题以及奇异值检测等实际问题中的应用。