基于2D-VMD和双边滤波的医学超声图像去噪算法

薛双青，贺东东

(山西省临汾市气象局，山西 临汾 041000)

0 引 言

在超声成像过程中会因信号的强弱与差异形成散斑噪声，会导致图像不清晰，降低超声图像的质量，由此图像去噪技术在其中起着至关重要的作用[1]。目前图像去噪方法一般分为2类：时间域和频率域的去噪方法，这些方法虽然有很好去除噪声的效果，但是存在边缘被过度平滑现象，造成了细节信息损失[2-3]。对于时间域的去噪方法来说，双边滤波算法具有良好的滤波效果和边缘保持特性。双边滤波器是一种非线性滤波器，能对空间邻近度和灰度相似度折衷处理，它将每个像素点的灰度值替换为邻近像素点灰度值的加权平均，邻近像素点所占的权重取决于它与中心像素点的空间欧氏距离和灰度相似度[4-6]。对于频域的去噪方法，2014年，研究学者提出基于经验模态分解(empirical mode decomposition，EMD)基础上改进的变分模态分解算法(variational modal decomposition，VMD)，该算法主要是通过变分方法来寻求每个固有模态分量的最优值，从而克服EMD的不足[7]。另外，VMD也被延伸到二维范围，即二维变分模态分解(two-dimensional variational modal decomposition，2D-VMD)方法。

二维变分模态分解能够很好地将其图像分解为低频分量和高频分量，另外双边滤波较其他滤波方法在处理超声图像来说，去除噪声和保留细节信息这两方面效果较好。为了克服几种常用方法在超声成像中去除噪声的缺点，文中主要是结合其2种方法的特点，提出一种将二维变分模态分解和双边滤波相结合的超声图像去噪的新方法。首先通过二维变分模态分解将图像分解成低频分量和高频分量，然后利用双边滤波对低频分量进行滤波处理，最后重构滤波后的分量。

1 二维变分模态分解

1.1 二维解析信号

(1)

对式(1)进行傅里叶变换得到谱域中的一维解析信号

(2)

(3)

对式(3)进行傅里叶变换得到谱域中的二维解析信号为

(4)

1.2 2D-VMD函数及求解uk和wk

1.2.1 2D-VMD函数

(5)

由此对式(5)转为约束最小模型作为目标函数来评估模态带宽即为二维VMD函数

(6)

采用的方法即乘法算子交替方向法(ADMM)，则得到非约束问题-扩展的拉格朗日函数[9]

L({uk},{wk},λ)=

(7)

由此求解无约束模型的鞍点即为某个方向的极大值或极小值。

1.2.2 求解及更新uk和wk

1)更新uk

对于求解及更新uk转化为在Ω中寻找uk使其公式(7)的函数值最小，其表达式为

(8)

根据卷积性质和傅里叶变换，将式(8)转化到频域中

(9)

另外将其中第1项调整为w→w-wk，式(9)转化为

(10)

对第1项进行调整是为了使真实信号的解析信号的带宽分布在正半平面w∈{〈w,wk〉>0}，根据式(4)，可将式(10)调整为

(11)

(12)

(13)

对式(13)进行傅里叶逆变换后的实数部分即为所对应的IMF分量uk。

2)更新wk

关于更新及求解wk，主要使其中心频率出现在带宽中，由此目标函数为

(14)

则式(14)变换到频域中的表达式为

(15)

然后令式(15)中积分部分对wk的偏导数等于零得出的wk值为其第n+1次更新的结果，其表达式为

(16)

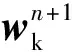
(17)

2 双边滤波算法

双边滤波是一种非线性滤波器，它可以达到保持边缘、降噪平滑的效果[10]。双边滤波的2个权重概念就是空间域与像素范围域。双边滤波的基本模型见式(18)(19)(20)

(18)

(19)

(20)

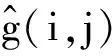
3 医学图像去噪算法原理及具体步骤

为了实现在去除噪声的同时能最大程度的保留原始图像特征，由此提出一种基于2D-VMD和双边滤波相结合的超声图像去噪算法，算法步骤如下。

步骤2：将灰度处理后的图像g(x,y)通过2D-VMD算法进行分解成k个模态分量IMF图像imgk(x,y)。

步骤3：将分解后的k个模态分量IMF图像imgk(x,y)通过评价指标系数筛选出有效的模态I图像分量。

步骤4：对有效的IMF图像分量进行双边滤波处理，得到去噪后的有效模态分量。

4 实验评价方法与结果分析

4.1 实验评价方法

对于评价滤波算法的效果以及性能，主要是由去噪和保护细节信息这2个方面来衡量的，由此将峰值信噪比(PSNR)和均方根误差(RMSE)分别作为判定去除噪声和保留细节信息的能力的指标[12]。

4.1.1 峰值信噪比

峰值信噪比作为衡量滤波算法去除图像噪声的能力的主要评价指标，该指标的值越大，说明滤波算法去除噪声能力较强[13]。其定义见式(23)。

(23)

4.1.2 均方根误差

RMSE作为评价图像质量的主要指标，主要是描述了原始图像与去噪图像在像素上的相似程度。若该值越小，相似程度越高，细节保持能力越强[14]。其定义见式(24)。

(24)

4.2 实验结果分析

该实验分别选取由Field工具模拟仿真生成超声胎儿和超声肾脏的2组图像[15]。由于在超声成像过程中噪声的不确定性，分别对二组不同特性的图像加入噪声方差为0.02和0.05[16]。另外，将维纳滤波、中值滤波、双边滤波、2D-VMD与中值滤波结合以及文中的方法应用于超声图像中，最后通过比较峰值信噪比和均方根误差2个系数来评价各种方法的去噪性能。

首先选取二组图像的噪声方差为0.05，比较分解后模态分量的评价指标并筛选出有效IMF分量，在二维变分模态分解中惩罚参数α=5 000，模态数k=4[17]。分解后的超声肾脏图像的模态分量以及模态分量对应频谱图，如图1、图2所示，分解后的超声胎儿图像的模态分量以及模态分量对应频谱图，如图3、图4所示。

从图1、图3可以看出，二组图像经分解后得到4个不同的模态分量，且每一个分量表示的是原始图像中不同频段的信息特征。从图2，图4可以得到，IMF1的中心频率位于中心位置，则其为低频分量，IMF2～IMF4的中心频率偏离中心位置，则其为高频分量。为了筛选出有效分量，由此比较二组图像中模态分量的峰值信噪比和均方根误差的值，见表1。

图1 超声肾脏的分解

图2 超声肾脏的IMF频谱

图3 超声胎儿的分解

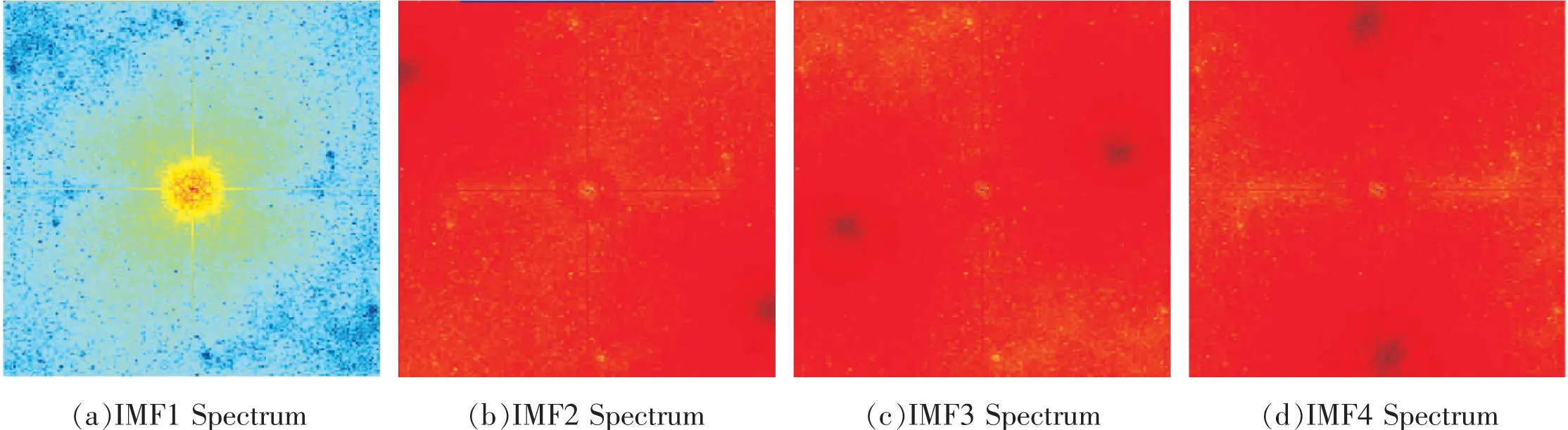
图4 超声胎儿的IMF频谱

表1 3组图像的各IMF指标

超声肾脏、超声胎儿二组图像中各模态分量的峰值信噪比和均方根误差的值差异比较大。第1模态分量IMF1的峰值信噪比最高、均方根误差最小，其他的模态分量IMF2、IMF3、IMF4的峰值信噪比较低而均方根误差较高，并且它们之间的值差异较小。由此可知，二组图像经分解后的第1模态分量能较好保留原始图像的信息特征且噪声成分较少，因此将其第1模态分量判定为有效分量；其他的模态分量IMF2、IMF3、IMF4的噪声成分较高，从而导致原始图像的信息特征损失，因此将其他的模态分量判定为噪声分量[18-21]。通过对超声肾脏以及超声胎儿二组图像的各模态分量进行对比，将其第1分量IMF1作为有效的模态分量，但其模态分量含有较少的噪声成分，需要对其有效分量进行双边滤波处理，最后对滤波后的有效分量进行重构即为去噪的图像。

为了验证该方法在超声图像处理中能否较好地在去除噪声的同时能更好地保留细节信息，将在不同方差(0.02，0.05)的噪声情况下，用4种方法对二组图像进行去噪处理并且采用峰值信噪比和均方根误差这2个指标作为衡量4种方法的去噪性能，4种方法PSNR值的对比见表2。

从表2可知，对于去噪后的方差为0.02的二组图像来说，文中方法与其他方法相比较，峰值信噪比最大且高出其他的方法大约1～0.2，说明该方法在去除噪声的效果方面优于其他的方法；从不同噪声密度来看，随着噪声密度的增加，文中方法在峰值信噪比这个方面比其它模型波动性要小，即其他的方法去噪性能受图像噪声密度影响较大。为了衡量各方法在保护细节方面的性能，5种方法RMSE值的对比见表3。

表2 PSNR的比较

从表3可知，在均方根误差方面，该方法与其他的方法相比较其均方根误差最小且与其他的方法相差大约1.1～0.2之间，表明该方法在保护细节信息方面优于其他的方法。综合表2，表3分析可知，在不同方差噪声情况下，该方法在峰值信噪比和均方根误差这两方面优于其他的方法，表明文中方法能在提高去噪效果的同时能够很好保留细节信息。

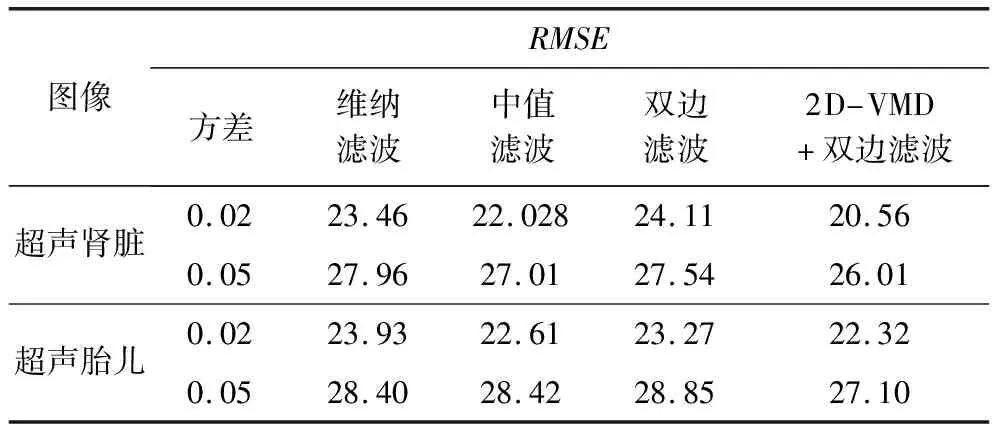
表3 RMSE的比较

为了更好地比较各方法在视觉上的效果，图5，图6分别表示是超声肾脏、超声胎儿在噪声方差为0.02情况下的各方法去噪的效果图。

从图5，图6可以看出，该方法将二维变分模态分解和双边滤波相结合应用于超声图像，其去噪效果优于其他的几种方法。

图5 超声肾脏的各方法对比

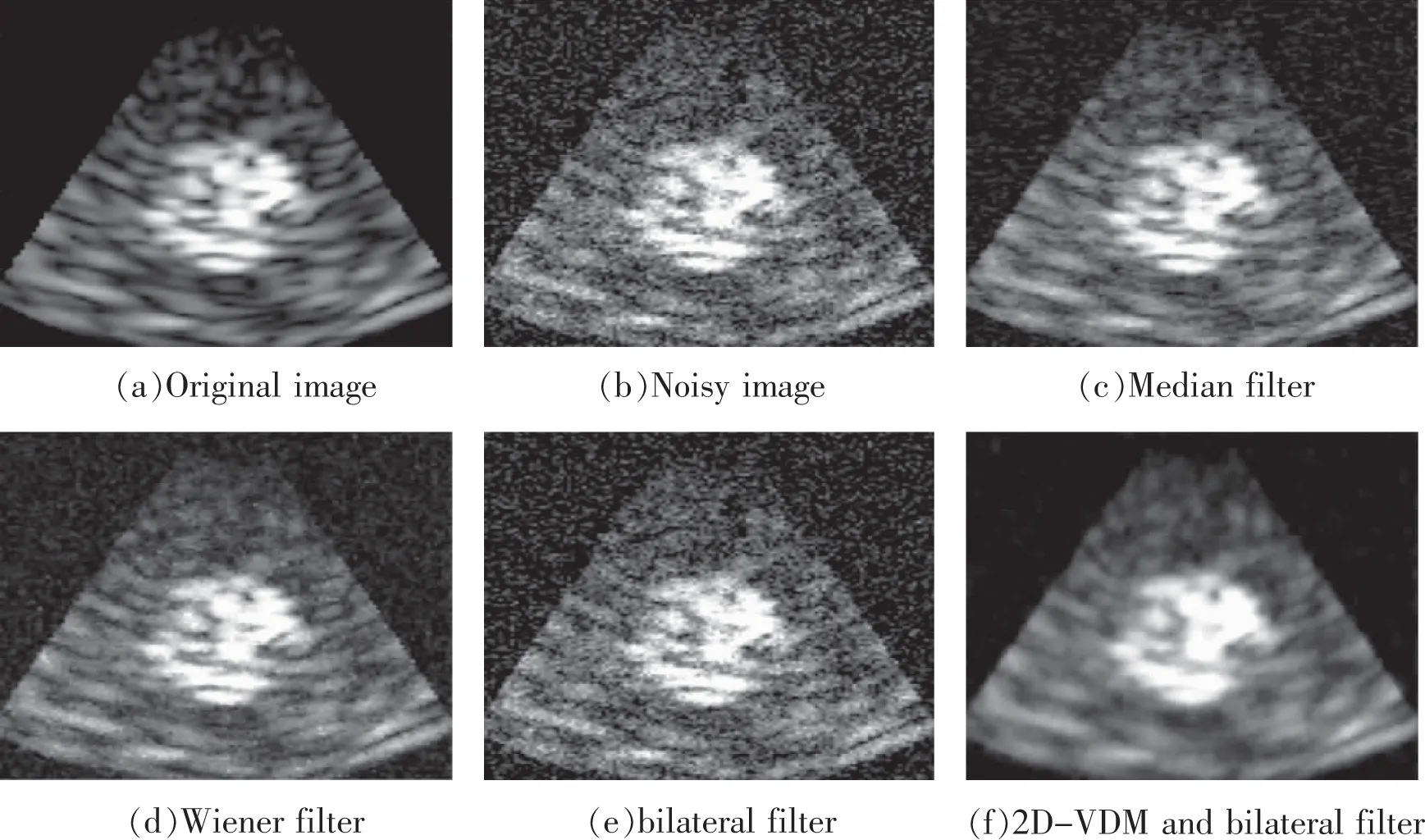
图6 超声胎儿的各方法对比

5 结 论

1)对于在抑制超声图像噪声和保护细节信息两方面的问题，提出基于2D-VMD和双边滤波的图像去噪算法，该算法主要是将二维变分模态分解和双边滤波相结合应用在超声图像处理中。

2)二维变分模态分解能够很好将其图像分解为低频分量和高频分量，双边滤波较其他滤波方法，在处理超声图像来说，去噪效果和保留细节信息这两方面效果较好；基于2D-VMD和双边滤波的超声图像去噪算法主要是结合2种方法的优点。

3)基于2D-VMD和双边滤波的超声图像去噪算法主要选取峰值信噪比和均方根误差作为衡量算法的性能指标。从实验结果来看，该算法在消除图像中的噪声和保留原有的细节内容这2个层面都优于其他的算法。

4)该方法在去除噪声方面效果不错，但是存在一些不足的地方，比如二维模态分解分解速度较慢、需要选择合适的模态分解个数[22-24]。