THE PROXIMAL RELATION,REGIONALLY PROXIMAL RELATION AND BANACH PROXIMAL RELATION FOR AMENABLE GROUP ACTIONS∗

(连媛)

College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China

E-mail:20140602035@cqu.edu.cn

Xiaojun HUANG(黄小军)†

College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China Chongqing Key Laboratory of Analytic Mathematics and Applications,Chongqing University,Chongqing 401331,China

E-mail:hxj@cqu.edu.cn

Zhiqiang LI(李智强)

College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China

E-mail:zqli@cqu.edu.cn

Abstract In this paper,we study the proximal relation,regionally proximal relation and Banach proximal relation of a topological dynamical system for amenable group actions.A useful tool is the support of a topological dynamical system which is used to study the structure of the Banach proximal relation,and we prove that above three relations all coincide on a Banach mean equicontinuous system generated by an amenable group action.

Key words Proximal relation;amenable group;mean equicontinuity

1 Introduction

Let X be a compact metric space with a metric d,and let T be a continuous map from X to itself.The pair(X,T)will be called a(topological)dynamical system;such a system can be regarded as a topological dynamical system for an action of integer groups.A dynamical system(X,T)is called equicontinuous if for every ε>0 there is a δ>0 such that whenever x,y∈X with d(x,y)<δ,d(Tnx,Tny)<ε for n=0,1,2...;that is,the family of maps{Tn|n∈Z+}is equicontinuous.The notion of stability in the mean,in the sense of Lyapunov,or simply mean-L-stable,was introduced by Fomin[12]when studying dynamical systems with a discrete spectrum;he proved that if a minimal system is mean-L-stable,then it is uniquely ergodic.In[25]Oxtoby proved that each transitive mean-L-stable system is uniquely ergodic.For additional accounts of this,see[1]and[32].If X has a compatible metric d,there is a family Ω of maps from X to itself;one can express this by saying that for every ε>0,there is a δ>0 such that for all f∈Ω and all x,y∈X satisfying d(x,y)<δ,one has d(f(x),f(y))<ε.In 2015,Li,Tu and Ye[22]introduced the concept of mean equicontinuity and proved that mean-L-stable is equivalent to mean equicontinuity.

When studying equicontinuous dynamical systems,the proximal relation P(X,T),the Banach proximal relation and the regional proximal relation play a significant role.It is well known that the system induced by the smallest closed T×T−invariant equivalence relation generated by P(X,T)is the maximal distal factor of(X,T)(see[2],for example).In general,however,P(X,T)is neither closed nor equivalent.For more about P(X,T),readers can also refer to[28].The author in[5]established the notion of a syndetically proximal relation SP(X,T)of(X,T).It is shown in[5]that SP(X,T)is an invariant equivalence relation in X,but it may not be closed.If P(X,T)is closed in X×X,then P(X,T)=SP(X,T)and P(X,T)is an invariant closed equivalence relation in X.Syndetically proximal pairs were studied in detail in[23,24].The paper[21]is devoted to the study of Banach proximal pairs BP(X,T)and the authors Li and Tu showed that BP(X,T)is an invariant equivalence relation.Clearly,if every set with Banach density one is syndetic,then a Banach proximal pair is syndetically proximal.Note that it is shown in[20]that for an interval map with zero topological entropy,every proximal pair is Banach proximal.In addition,a regional proximal relation is introduced in[11]and it is shown that the equicontinuous structure relation is the smallest closed invariant equivalence relation containing the regional proximal relation,and the distal structure relation is the smallest closed invariant equivalence relation containing the proximal relation.

Using the properties of unique ergodicity,Li,Tu and Ye[22]proved that for a mean equicontinuous system(X,T),a pair of points is proximal if and only if it is Banach proximal and if and only if it is regionally proximal,the collection of all proximal pairs is a closed invariant equivalence relation.They also proved that a mean equicontinuous system has a discrete spectrum using the above basic fact,so the topological entropy of(X,T)is zero.Later they introduced the Banach mean equicontinuity concept,with which the dynamical system has better properties.We know that Banach mean equicontinuity is equivalent to mean equicontinuity,as was proved by Downarowicz and Glasner[7]for a minimal system,and by Qiu and Zhao[30]for general cases of Z-actions.It is not difficult to see that a Banach mean equicontinuous system is a mean equicontinuous system.Therefore,the topological entropy of a Banach mean equicontinuous system is also zero.We refer the reader to the textbook[35]and the paper[14]for the basic properties of topological entropy.For even more information,please refer to[9,10,26,27,36].

A natural question now is:what would be the situation in a Banach mean equicontinuous system for amenable group actions?We show that this question has a good answer.In[18],cka and Pietrzyk studied the Banach density of amenable group actions.Their results give quite a number of contributions to dealing with the Banach mean equicontinuity of amenable group actions(see[38]and[13]).Wely-mean equicontinuity is introduced in[13]and the paper[38]defined Banach mean equicontinuity.Stimulated by these two papers,we have the a number of results.Firstly,we make use of Banach density to define the concept of mean-L-stable,and observe that Banach mean equicontinuity is equivalent to the mean-L-stability.Furthermore,we introduce notion of the support of a topological dynamical system and study the structure of the Banach proximal relation using this useful tool.Finally,we prove that three relations all coincide in a Banach mean equicontinuous system.

Theorem 1.1Let G be a countable discrete amenable group and let X be a compact metric space.Let G↷X be a continuous action.If the action G↷X is Banach mean equicontinuous,then

and it is a closed invariant equivalence relation.

We organize this paper as follows:Section 2 gives some basic notions which we will use in this paper.In Section 3,we study the unique ergodicity and Banach mean equicontinuity and obtain several equivalent conditions of unique ergodicity for the amenable group action dynamical system.In Section 4,we study the support of a dynamical system for amenable group actions and show its connection with the subsets of amenable group G with some kind of density.This property is very useful in the discussion of the structure of the Banach proximal relation.Finally,Section 5 is devoted to studying the relationship of the proximal relation,the regionally proximal relation and the Banach proximal relation.Moreover,we establish an analogue of Theorem 3.5 in[22]for the Banach mean equicontinuous system for amenable group actions.

2 Preliminaries

By an action of the group G on a set X we mean a map α:G×X→X such that,writing the first argument as a subscript,αs(αt(x))=αst(x)and αe(x)=x for all x∈X and s,t∈G.Most of the time we will write the action as G↷X with the image of a pair(s,x)written as sx.We refer the reader to the textbook[16]for more information on following statements:

Definition 2.1([16,Definition 1.2]) By a p.m.p.(probability-measure-preserving)action of G,we mean an action of G on a standard probability space(X,µ)by measure-preserving transformations.In this case,we will combine the notation and simply write G↷(X,µ).

Given an action G↷X on a set X,we say that a set A⊆X is G-invariant if GA=A,which is equivalent to GA⊆A.When the action is probability-measure preserving and A is a measurable set,we interpret G-invariance to mean GA=A modulo a null set,that is,µ(sA△A)=0 for all s∈G.

Given two actions G↷X and G↷Y on ordinary sets,we can form the product action G↷X×Y by setting s(x,y)=(sx,sy)for all(x,y)∈X×Y and s∈G.If G↷(X,µ)and G↷(Y,ν)are p.m.p.actions,then so is the product action with respect to the probability measureµ×ν.

Let G be a group.A mean for G on ℓ∞(G)is a unital positive linear functional σ:ℓ∞(G)→C(unital means that σ(1)=1).The mean σ is left invariant if σ(sf)=σ(f)for all s∈G and f∈ℓ∞(G),where(sf)(t)=f(s−1t)for all t∈G.

Definition 2.2The group G is said to be amenable if there is a left invariant mean onℓ∞(G).

The above definition of a countable amenable group G is equivalent to the existence of a sequence of finite subsets{Fn}of G which is asymptotically invariant,that is,

where gFn={gf:f∈Fn},|·|denotes the cardinality of a set,and Δ is the symmetric difference.Such sequence is called a(left)Følner sequence.A sequence of finite subsets{Fn}of G is a right Følner sequence if

It is called a two-sided Følner sequence if both conditions hold.

The class of amenable groups contains,in particular,all finite groups,all abelian groups and,more generally,all solvable groups.

Throughout this paper,the group G is countable discrete amenable and X is a compact metric space with metric d.

Any dynamical system admits invariant probability measures and the ergodic measures can be shown to be the extremal points of the set of invariant probability measures(see,for example,the monographs[6,35]).Let M(X),MG(X),and(X)denote the sets of all Borel probability measures on X,G-invariant regular Borel probability measures on X,and ergodic measures in MG(X),respectively.Let C(X)be the set of continuous real functions on X with the supremum norm‖f‖∞=supx∈X|f(x)|.We regard M(X)as a closed convex subset of C(X)∗,which is the dual space of C(X),equipped with the weak*topology.Then M(X)is a compact metric space.

In this section we recall some notions which were introduced and discussed by[4]and[8].

Let E⊆G.The upper asymptotic density of E with respect to a Følner sequence F={Fn}n∈N,denoted by(E),is defined by

Similarly,the lower asymptotic density of E with respect to a Følner sequence F={Fn}n∈N,denoted by(E),is defined by

One may say that E has asymptotic density dF(E)of E with respect to a Følner sequence F={Fn}n∈Nifin which dF(E)is equal to this common value.In our further considerations,we need the notion of Banach density,which we now briefly recall.

Let Fin(G)be the family of all non-empty finite subsets of G.The upper Banach density of E is defined as

If{Fn}n∈Nis a Følner sequence,then we have(see[8,Lemma 2.9])

In particular,given that the above limit exists and does not depend on the choice of{Fn}n∈N,it follows from(2.1)that(2.2)give us

where the supremum is taken over all Følner sequences F={Fn}n∈N.

The lower Banach density of E is given by BD∗(E)=1−BD∗(GE).

Clearly,for any E⊆G,one has BD∗(E)≤BD∗(E).If BD∗(E)=BD∗(E),then we say that there exists the Banach density of E and denote it by BD(E).It is not difficult to observe the following:

Lemma 2.3Let F,F1,F2be subsets of G and s∈G.Then

1.If F1has Banach density one and F1⊆F2,then so does F2.

2.If F has Banach density one,then GF is a set of Banach density zero.

3.If F1and F2have Banach density one,then so does F1∩F2.

4.If F has Banach density one,then so does Fs.

3 Unique Ergodicity and Banach Mean Equicontinuity

In 2015,Li,Tu and Ye[22]showed that for a system the notions of mean equicontinuity and mean-L-stable are equivalent for Z+-actions.Inspired by[22],we will introduce notions of mean-L-stablity on a dynamical system generated by an amenable group action,and we get a similar relation between Banach mean equicontinuity and mean-L-stablity.After that,we study uniquely ergodic systems and Banach mean equicontinuous systems for amenable group actions.We obtain several equivalent conditions of a uniquely ergodic system.We also state some properties of Banach mean equicontinuous systems for a countable discrete amenable group action.

Definition 3.1([38]) Let G be a countable discrete group and let X be a compact metric space with metric d.For x,y∈X,we denote

Thus we say that the action G↷X is Banach mean equicontinuous or simply B-mean equicontinuous if,for any ε>0,there is a positive real number δ>0 such that<ε whenever d(x,y)<δ for x,y∈X.

In[13],Fuhrmann,Gröger and Lenz introduced the concepts Besicovitch-and Weyl-mean equicontinuity for amenable action systems.

Definition 3.2Let G be an amenable group and F={Fn}n∈Nbe a Følner sequence of G.We say that the action G↷X is Besicovitch-F-mean equicontinuous if,for every ε>0,there exists δ>0 such that

for all x,y∈X with d(x,y)<δ.The dependence on the Følner sequence immediately motivates the next definition.We say that the action G↷X is Weyl-mean equicontinuous if,for every ε>0,there exists δ>0 such that,for all x,y∈X with d(x,y)<δ,we have

For the relationship between Banach mean equicontinuity and Weyl-mean equicontinuity,we have the following result:

Proposition 3.3When G is a countable discrete amenable group,Banach mean equicontinuity and Weyl-mean equicontinuity are equivalent.

For proof of Proposition 3.3,please refer to[38].

Remark 3.4The definition of Banach mean equicontinuity may seem to depend on the particular choice of the metric.However,by the compactness of the underlying space X,it turns out to hold for one metric if and only if it holds for any metric(which induces the same topology).

Definition 3.5The action G↷X is called stable in the mean in the sense of Lyapunov or simply mean-L-stable if,for every ε>0,there is a positive real number δ>0 that implies d(gx,gy)<ε for all g∈G,except a set of upper Banach density less than ε.

Now we show that Banach mean equicontinuity is equivalent to the mean-L-stability of the systems for amenable group actions.

Lemma 3.6Suppose that G is an amenable group.Let G↷X be a continuous action.Then the action is B-mean equicontinous if and only if it is mean-L-stable.

ProofAssume that the action G↷X is B-mean equicontinuous.By Proposition 3.3,we know that G↷X is Weyl-mean equicontinuous.

Let ε>0.Then there is a positive real number δ>0 such that,whenever x,y∈X with d(x,y)<δ,

Take two points x,y∈X with d(x,y)<δ.Let E={g∈G:d(gx,gy)≥ε}and F={Fn}n∈Nbe any Følner sequence of G.It follows that

The arbitrariness of Følner sequence F and equation(2.3)implies that

where the sumpremum is taken over all of the Følner sequence F of G.Thus BD∗(E)<ε,which implies that the action G↷X is mean-L-stable.

Conversely,assume that the action G↷X is mean-L-stable.Take a positive number ε>0.We choose a positive real numberThen there is a positive real number δ>0 such that

for all g∈G,except for a set of upper Banach density less than η.

Take two points x,y∈X with d(x,y)<δ.Let F={Fn}n∈Nbe a Følner sequence of G,and let E={g∈G:d(gx,gy)≥η}.By the condition BD∗(E)<η,we get

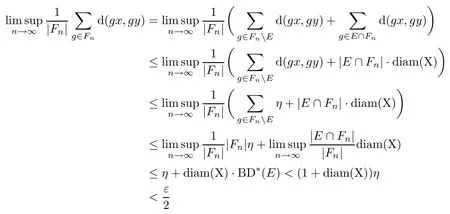
that is,DF(x,y)<ε/2.From the arbitrariness of Følner sequence F,it follows that

which implies that the action G↷X is B-mean equicontinuous. □

In order to obtain our results,we need the following well-known theorems:

Theorem 3.7([35,Theorem 6.2,p.147]) Let m,µbe two Borel probability measures on the compact metric space X.If

Theorem 3.8([31,Krein-Milman Theorem]) Let C be a nonempty compact convex subset of a HausdorffLCS(locally compact space).Then C is the convex hull of its set of extreme points

Remark 3.9Let X be a compact metric space.Let G be a countable group with a continuous action on X.If MG(X)/=∅,by the Krein-Milman Theorem,we have that

The next theorem relates elements of M(X)to linear functionals on C(X).

Theorem 3.10(Riesz Representation Theorem) Let X be a compact metric space and J:C(X)→C a continuous linear map such that J is a positive operator(that is,if f≥0,then J(f)≥0)and J(1)=1.Then there existsµ∈M(X)such that

We recall that the action G↷X is uniquely ergodic if it admits exactly one G-invariant Borel probability measure.In particular,if a dynamical system admits only one invariant probability measure,then,by Theorem 3.8,this measure is automatically ergodic.In this case the dynamical system is uniquely ergodic.

Let G↷X be a continuous action and let f∈C(X).We denote

where F is a nonempty finite subset of G.We then have the following theorem:

Theorem 3.11Let G be a countable amenable group and let X be a compact metric space.Suppose that G↷X is a continuous action.Then the following conditions are equivalent:

1.the action G↷X is uniquely ergodic;

2.for each two-sided Følner sequence{Fn}n∈Nof G and for every f∈C(X),converges uniformly on X to a constant;

3.for each two-sided Følner sequence{Fn}n∈Nof G and for every f∈C(X),there is a sub-family{Fni}⊆{Fn}such thatconverges pointwise on X to a constant.

Proof(1)⇒(2)Letµbe the uniquely ergodic measure of the dynamical system G↷X,and let{Fn}n∈Nbe a two-sided Følner sequence for G.

ClaimFor each f∈C(X),the sequenceconverges uniformly on X toRfdµas n→∞.

Suppose that the conclusion is false.Then there exist a function g∈C(X),a positive real number ε0>0,a sequence of positive integers ni≥i and a sequence of points{xi}⊆X such that−Rgdµ|≥ε0>0.It is clear that the numerical sequenceis bounded by‖g‖∞,so by the Bolzano-Weierstrass Theorem,it has a convergent subsequence.Without loss of generality,we may assume that

Note that C(X)is a separable metric space,since X is a compact metric space.Thus we can choose a countable dense set S of C(X)as S={f1=g,f2=1,f3,f4,···,fn,···}.

The next proof is a standard diagonal argument.Note that the numerical sequence

Hence we get a countable collection of subsequences of N as follows:

It is clear that L is positive on S(that is,if f∈S and f≥0,then L(f)≥0).

Next,we extend L to all finite linear combinations Z=span{f1=g,f2=1,f3,f4,···}of elements of S to preserve linearity.

Denote GZ={sf:s∈G,f∈Z}.Let s∈G and f∈Z.Since{Fn}n∈Nis a two-sided Følner sequence of G,one has that

This fact implies that if f,sf∈S for s∈G,then L(sf)=L(f).Thus we can extend L to GZ by L(sf):=L(f)for s∈G,f∈Z.Furthermore,if sf=tg for f,g∈S and s,t∈G then f=(t−1s)g and

The above equality shows that the linear operator L is well defined on GZ.

Note that GZ is also dense in C(X).Thus,for any f∈C(X),there exists{}⊆GZ such that‖−f‖→0 as j→∞.It is obvious that=sjfjfor some sj∈G and fj∈S.It is not hard to verify that

It is easy to see that the definition of L is independent of the choice of the sequence of{~fj}⊆GZ.Furthermore,it is not hard to verify that L is linear operator on C(X)and L(1)=1.

Now we show that L is positive(that is,if f≥0,then L(f)≥0).Otherwise,there exist a continuous function f≥0 and a positive real number δ>0 such that L(f)<−δ.Recall that S is dense in C(X).Then there is a sequence of continuous functions{fj}⊆S satisfying that‖fj−f‖∞→0 as j→∞.Thus<−δ.Furthermore,there exists N∈N such thatfor j≥N;that is,fj(x)>f(x)−for j≥N and x∈X.Therefore,for j≥N,we have

Thus,since fj∈S,one has

Hence,

which is a contradiction.

Therefore,L is a positive linear operator and L(1)=1.By Theorem 3.10(Riesz Representation Theorem),L(f)=Rfdν for some Borel probability measure ν.

Now,we show that ν is G-invariant.Given s∈G,f∈C(X),there exists{fj}⊆Z such that‖fj−f‖→0 as j→∞.Then{s−1fj}⊆GZ and‖s−1fj−s−1f‖=‖fj−f‖→0 as j→∞.Thus,we have

Therefore ν is G-invariant.Since the action G↷X is uniquely ergodic,ν=µ.Noting that g∈S and considering equality(3.2),one has

Hence,α=Rgdµ,which is a contradiction.Thus our desired result is obtained.

(2)⇒(3)is obvious.

(3)⇒(1)The arguments for what follows are similar to the discussions in(1)⇒(2).

Recall that C(X)is separable,since X is compact.Thus we can choose a countable dense set S of C(X)as S={f1=1,f2,f3,f4,···,fn,···}.

Let{Fn}n∈Nbe a two-sided Følner sequence of G.For the function f1∈C(X),the assumption shows that there exists a sequence of positive integers of⊆N satisfying that

for some constant c1∈R.

For the two-sided Følner sequence ofand the function f2∈C(X),the assumption implies that there exists a sequence of positive integers ofsatisfying that

for some constant c2∈R.

Proceeding in this fashion,we can obtain a sequence of positive integers ofsuch that

for some constant cl∈R.Now,we denote thatfor all l∈N.With the same arguments as in the proof of(1)⇒(2),we can define a linear operator L:S→R as follows:

In the same manner as the discussion above,we can extend the operator L to C(X)such that L is a positive linear operator from C(X)into R and L(1)=1.By Theorem 3.10(Riesz Representation Theorem),L(f)=Rfdν for some Borel probability measure ν.It is not hard to verify that ν is G-invariant.

Letµ∈MG(X)be any G-invariant measure.For any fj∈S,we have

Sinceµis G-invariant,one hasRfj(sx)dµ=Rfj(x)dµ.Hence we get

Using a bounded control convergence theorem,we can deduce that

Since S is dense in C(X),we get ∫ fdµ=∫ fdν for all f∈C(X).Hence ν=µ,by Theorem 3.7.Therefore the action G↷X is uniquely ergodic. □

The following lemma is easy to verify:

Lemma 3.12Let G↷X be a continuous action.Then the action G↷X×X is B-mean equicontinuous if and only if the action G↷X is B-mean equicontinuous.

For our purposes,we state the following well-known result:

Theorem 3.13(The Arzela-Ascoli Theorem) If a sequencein C(X)is bounded and equicontinuous,then it has a uniformly convergent subsequence.In this statement,we note that

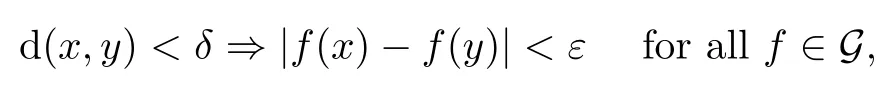
where d is the metric on X.

For the rest of this paper,we need the following concepts and theorems that appeared in[13]:

Definition 3.14Let G↷X be a dynamical system.If G↷X has an unique ergodic measure,then G↷X is called uniquely ergodic.A system G↷X is pointwise uniquely ergodic if the orbit closure Gx of every point x∈X is uniquely ergodic.

Theorem 3.15([13,Theorem 3.4]) Let G be a discrete countable amenable group and let X be a compact metric space.Assume that G↷X is Weyl-mean equicontinuous.Then G↷X is topo-isomorphic to its maximal equicontinuous factor G↷T.

Theorem 3.16([13,Theorem 3.14]) Let G be a discrete countable amenable group and let X be a compact metric space.Assume that G↷X is topo-isomorphic extension of an equicontinuous system G↷Y with factor map h:X→Y.Then G↷X is pointwise uniquely ergodic.

By Proposition 3.3,Theorem 3.15 and Theorem 3.16,we can immediately get the following corollary:

Corollary 3.17Let the action G↷X be B-mean equicontinuous.Then,for every x∈X,G↷is uniquely ergodic.

A point x∈X is generic forµ∈MG(X)with respect to a Følner sequence{Fn}n∈Nif

where δxdenotes the Dirac measure supported at x.

A Følner sequence{Fn}n∈Nis called tempered if,for some C>0 and all n∈N,one has

Every Følner sequence has a tempered subsequence(see[19,Proposition 1.4]).In particular,every amenable group has a tempered Følner sequence.It follows from the ergodic Theorem for amenable group actions(see[19,Theorem 1.3])that given any tempered Følner sequence{Fn}n∈Nand any ergodic measureµ,one can find a generic point forµwith respect to{Fn}n∈N.

In order to prove our main results,we need the following characterization of generic points:

Proposition 3.18Let G be a countable amenable group and let X be a compact metric space.Let G↷X be a continuous action and let m∈be an ergodic measure.Then,for any tempered Følner sequence{Fn}n∈Nof G almost every point of X(with respect to m)is generic for m with respect to{Fn}n∈N.

ProofThis follows directly from[19,Theorem 1.2]. □

4 The Support of a Dynamical System

In this section,we study the support of a dynamical system and show its connection with the subsets of G with some kind of density.This property is very useful in the discussion of the structure of the Banach proximal relation.

Let(X,d)be a compact metric space,with Borel σ-algebra B.Denote by M(X)the space of Borel probability measures on X.Our main interest is the weak-∗topology of space M(X),which is standard(for more on this see Pathasarathy[29]).

Theorem 4.1Let X be compact metric space and{µn}be a sequence of probability measures in M(X).Letµ∈M(X).Then the following statements are equivalent:

The support of a measureµ∈M(X),denoted by supp(µ),is the smallest closed subset C of X such thatµ(C)=1(see[33]);that is,

The following proposition is well known:

Proposition 4.2We have

Let x∈X and let U be an open subset of X.Put G(x,U)={g∈G:gx∈U}.

Definition 4.3Let K be a compact subset of compact metric space X.We say that K has a BD property if,for any x∈X and for any open neighborhood U of K,G(x,U)has Banach density one.Here G(x,U)={g∈G:gx∈U}.

The support of an action G↷X,denoted by supp(G↷X),is defined by the intersection of all compact subsets with a BD property of X;that is,

Note that the support of a dynamical system is also called the measure center in[37].We denote

In order to prove supp(G↷X)=A,we need the following facts:

Proposition 4.4For eachµ∈MG(X),one hasµ(A)=1.

ProofFor every K∈KG,it is clear thatµ(K)=1,which implies that supp(µ)⊆K.It follows that

Thusµ(A)≥µ(supp(µ))=1.Hence the proposition is obtained. □

On the other hand,A is closed from the definition of A andµ(A)=1 for allµ∈MG(X).From Proposition 4.4,one has supp(µ)⊆A,and hence we obtain the required property. □

Lemma 4.6Let G be a countable amenable group and let X be a compact metric space.Let G↷X be a continuous action.Suppose that x∈X and that F is a subset of G with positive upper Banach density.Then there exists an invariant measureµ∈MG(X)such that

Proofα0be the upper Banach density of F and let{Hn}be a Følner sequence of G.Then,by equality(2.2),we get

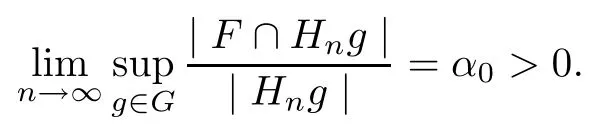
Thus,for large enough n,we have

Hence,there exists gn∈G such that

which means that

Set

where δxdenotes the Dirac measure supported at x.By the compactness of M(X),there is a convergent subsequenceof{µn}which converges to a Borel probabilityµ∈M(X)in the weak*-topology.For any f∈C(X)and any s∈G,we have

Hence the lemma is proved. □

Lemma 4.7Let G be a countable amenable group and let X be a compact metric space.Let G↷X be a continuous action and let{Fn}n∈Nbe a Følner sequence of G.Suppose thatµ∈MG(X).If a point y∈supp(µ)is generic forµwith respect to{Fn}n∈N,then for every open neighborhood U of y,G(y,U)has positive lower asymptotic density with respect to{Fn}n∈N.

ProofFix an open neighborhood U of y.By Uryson’s Lemma,there is a continuous function f∈C(X)such that 0≤f(x)≤1 for all x∈X,f(y)=1 and f(x)=0 for x∈Uc.Then

Owing to the fact that f is continuous and that f(y)=1,there exists an open neighborhood V⊆U of y such that f(x)>1/2 for every x∈V.Due to that fact that y∈supp(µ),it follows thatµ(V)>0.Combining this with f≥0,we get thatRfdµ>0.Since y is a generic point forµwith respect to{Fn}n∈N,we have

Thus

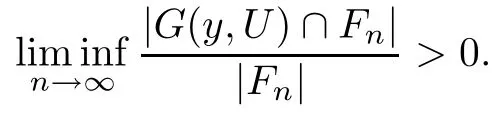
Therefore G(y,U)has a positive lower asymptotic density with respect to{Fn}n∈N. □

Now we can prove our main result of this section.

Proposition 4.8Let G be a countable amenable group and let X be a compact metric space.Then A=supp(G↷X).

ProofWe need three steps to finish the proof.

Step 1We will show that A has a BD property.

Suppose that A has NO BD property.Then there exist a point x0∈X and an open set U0⊇A such that G(x0,U0),whose lower Banach density is less than one.Thus G(x0,)has positive upper Banach density.By Lemma 4.6,there exists an invariant measureµ∈MG(X)such thatµ()>0.Sinceµ(supp(µ))=1,we getµ(∩supp(µ))>0.Hence,it follows that

By Proposition 4.5,one has supp(µ)⊆A⊆U0,which is a contradiction.

Step 2We will prove that supp(µ)⊆supp(G↷X)for eachµ∈MG(X).

Take an invariant measureµ∈MG(X).Suppose that supp(µ)∩(Xsupp(G↷X))/=∅.Then there is a point x0∈supp(µ)∩(Xsupp(G↷X)).By the definition of supp(G↷X),there is a closed subset K0with a BD property and x0∈XK0.Since X is a compact metric space,there exist open sets U⊇K0and V∋x0with U∩V=∅.Noting that x0∈supp(µ),one has thatµ(V)>0.By the ergodic decomposition ofµ(see[34,Theorem 4.2,p.208]and[17,p.738-739]),there exists an ergodic invariant measure ν∈(X)such that ν(V)>0.Hence ν(V∩supp(ν))>0.

Let{Fn}n∈Nbe a tempered Følner sequence of G.By Proposition 3.18,there is a point z0∈V∩supp(ν)which is a generic point for ν with respect to{Fn}n∈N.Then,applying Lemma 4.7,we know that G(z0,V)has a positive lower asymptotic density with respect to{Fn}n∈N.Since the positive upper Banach density of G(z0,V)does not depend on the choice of Følner sequence,G(z0,V)has positive upper Banach density.Hence the lower Banach density of G(z0,XV)is less than one.From the BD property of K0,G(z0,U)has a Banach density of one.Meanwhile,U∩V=∅implies that G(z0,U)⊆G(z0,XV).Hence the lower Banach density of G(z0,XV)equals 1,which is a contradiction.

Step 3A=supp(G↷X).

From Step 1 and Step 2,we have that

Lemma 4.9Let G be a countable amenable group and let X be a compact metric space.Suppose that G↷X is a continuous action.Then there exists an invariant measure∈MG(X)such that supp(~µ)=supp(G↷X).

Lemma 4.10Let G be a countable amenable group and let X be a compact metric space.Suppose that G↷X is a continuous action.Then

Remark 4.11It should be noticed that the measure in Lemma 4.9 may not be ergodic.For example,taking X={a,b}and the identity map of the group action G={e}on X,it is easy to see that the dynamic system G↷X has only two ergodic measures,m and ν,which satisfy that m({a})=1,m({b})=0 and ν({a})=0,ν({b})=1.Thus,by Lemma 4.10,it follows that

Define an G-invariant probability measure τ on X as follows:τ({a})=τ({b})=It is clear that τ is not ergodic,but that supp(τ)=X.

In fact,we have the following characterization of an orbit of a point:

Proposition 4.12Let G be a countable amenable group and Let X be a compact metric space.Suppose that G↷X is a continuous action and that x∈X.Then y∈suppif and only if,for every open neighborhood U of y,G(x,U)has positive upper Banach density.

ProofFor convenience,we assume thatLet y∈supp(G↷X)and let U be an open neighborhood of y.By Lemma 4.10,there exists an ergodic invariant measureµsuch thatµ(U)>0.Sinceµ(supp(µ))=1,we get thatµ(U∩supp(µ))>0.

Let{Fn}n∈Nbe a tempered Følner sequence of G.Sinceµ(U∩supp(µ))>0 and on account of Proposition 3.18,there is a generic point z∈U∩supp(µ)forµwith respect to{Fn}n∈N.Then G(z,U)has a positive lower asymptotic density with respect to{Fn}n∈N.According to equation(2.3),we know that G(z,U)has positive upper Banach density.

Let W be a finite subset of G(z,U).For any g∈W,it is clear that gz∈U.By the continuity of G↷X there exists an open neighborhood V of z such that gV⊂U for all g∈W.Sincethere is an element tW∈G such that tWx∈V;that is gtWx∈U for all g∈W.This implies that WtW⊂G(x,U).

ClaimFor any finite subset W⊆G(z,U),if there exists a tW∈G such that WtW⊂G(x,U),then G(x,U)has positive upper Banach density.

Note that G(z,U)has positive lower asymptotic density with respect to the above tempered Følner sequence F={Fn}n∈N.Take

Then there exists N1∈N such that

for all n≥N1.Now we claim that G(x,U)has positive upper Banach density.Otherwise,we would have

Thus,for above∊0>0,there is N2∈N such that

Now,let N=max{N1,N2}+1 and W=FN∩G(z,U).According to inequality(4.1),it follows that

Meanwhile,since WtW⊂G(x,U)for some tW∈G and because of inequality(4.2),one has that

which contradicts inequality(4.3).Hence G(x,U)has positive upper Banach density.

Now we prove the necessity of the proposition.Let y∈X satisfy that,for every open neighborhood U of y,G(x,U)has positive upper Banach density.

Let U be an open neighborhood of y.Then there is an open neighborhood U′of y withThe assumption shows that G(x,U′)has positive upper Banach density.Then,by Lemma 4.6,there exists an invariant measureµ∈MG(X)such thatThereforeµ(U)>0.The arbitrariness of U implies that y∈supp(µ).Sinceµis an invariant measure and Proposition 4.5,we have y∈supp(G↷X). □

5 Three Kinds of Relations

It was shown in[1]that a pair of points is proximal if and only if it is persistently proximal(proximal with density one)in a mean equicontinuous system.Subsequently,Li-Tu-Ye[22]strengthened this result.

Given Li-Tu-Ye’s work,it is natural to ask how to define Banach proximal pairs and regionnally proximal pairs for actions of countable amenable groups on compact metrizable spaces,and whether their relations coincide with the proximal relations.The goal of this section is to answer these questions.First,using the support of the orbit closure,we have the three equivalent conditions of Banach proximal pairs.We show that a pair of points is Banach proximal if and only if the support of the closure of the orbit of the pair in the product system is contained in the diagonal.Finally,we study properties deriving from the regionally proximal relation of a Banach mean equicontinuous system for amenable group actions is equal to the Banach proximal relation,which is the same as the proximal relation.

Definition 5.1A pair of points(x,y)∈X×X is said to be proximal if=0.Let P(G↷X)denote the collection of all proximal pairs for the action G↷X.The action G↷X is proximal if any pair of points in X is proximal;that is,P(G↷X)=X×X.If>0,then it is said to be distal.An action G↷X is distal if any pair of distinct points in X is distal.

A pair of points(x,y)∈X×X is said to be Banach proximal if,for any ε>0,d(gx,gy)<ε for all g∈G,except for a set of zero Banach density.Let BP(G↷X)denote the collection of all Banach proximal pairs for the action G↷X.

A pair of points(x,y)∈X×X is called regionally proximal if,for any ε>0,there exist two points x′,y′∈X with d(x,x′)<ε and d(y,y′)<ε,and g∈G such that d(gx′,gy′)<ε.Let Q(G↷X)be the set of all regionally proximal pairs for the action G↷X.

Clearly,Q(G↷X)⊇P(G↷X)⊇BP(G↷X).

Remark 5.2(see[3]) The following propositions are easy to verify:

In this section,we study the structure of the Banach proximal relation.Using the support of the orbit closure,we have the following equivalent conditions of Banach proximal pairs:

Proposition 5.3Let G be a countable amenable group and let X be a compact metric space.Let ΔXdenote the diagonal of X2.Suppose that G↷X is a continuous action and that(x,y)∈X2.Then the following conditions are equivalent:

Proof(1)⇒(2)To finish the proof,we need the following steps:

Step 1We show that for any open neighborhood U of ΔX,there is a positive real number ε0>0 such that

Otherwise,there exists an open neighborhood U of ΔX,and(an,bn)∈X×X satisfies d(an,bn)<,but(an,bn)∈XU.We note that X is a compact metric space;that is,X is a limit point compact metric space,so there is an a∈X with an→a as n→∞.Hence d(an,a)→0 as n→∞.Since d(an,bn)<,d(bn,a)→0 as n→∞.Thus(an,bn)→(a,a)as n→∞for some(a,a)∈ΔX⊆U.This implies that(an,bn)∈U for large enough n,which is a contradiction.

Step 2We prove that for any open neighborhood U of ΔX,G((x,y),U)has Banach density one.

Let U be an open neighborhood of ΔX.By Step 1,there is a positive real number ε0>0 such that

and(x,y)is Banach proximal.This means that{g∈G:d(gx,gy)<ε0}has Banach density one.Consequently,{g∈G:(gx,gy)∈U}has Banach density one.

whenever f∈C(X)and f≥χK.Note that XK is an open set.It follows from Proposition 5.4 that

Given g0∈C(X),0≤g0≤χXKand supp(g0)⊆XK,we have that 1−g0≥1−χXK=χKand that 1−g0is continuous.By equation(5.1),we get thatRg0dµ≤1−α.Hence,

Thereforeµ(K)≥α>0,which contradicts the fact thatµ(K)=0.Hence the proposition is obtained. □

Li-Tu-Ye studied the propositions pertaining to the collection of all proximal pairs,the collection of all Banach proximal pairs,and the set of all regionally proximal pairs in(X,T),and they also obtained an interesting result in[22].In a fashion similar to Theorem 3.5 in[22],we have the following result:

Theorem 1.1Let G be a countable discrete amenable group and let X be a compact metric space.Let G↷X be a continuous action.If the action G↷X is B-mean equicontinuous,then

and it is a closed invariant equivalence relation.

ProofIt is clear that Q(G↷X)⊃P(G↷X)⊃BP(G↷X).We are going to show that

By Step 1 of the proof of Proposition 5.3,there is a positive real number ε0>0 such that

From the definition of the proximality of(x,y),there exists s∈G such that d(sx,sy)<ε0,which implies that

Therefore,O∩G(x,y)/=∅which contradicts the fact thatHence,our claim is obtained;that is,

From Proposition 5.5,we get that ν(K)>0;that is,ν(K)=1.From the definition of support of ν,it follows that supp(ν)⊆K.Since ν is unique ergodic and because of Lemma 4.10,we have that

By Proposition 5.3,we deduce that(x,y)∈BP(G↷X).Thus we obtain that

Assume now that(x,y)∈Q(G↷X).Let ε>0.Owing to the action G↷X being B-mean equicontinuous,there exists δ1>0 such that

Let F={Fn}n∈Nbe a two-sided Følner sequence of G.Thus we have

Since(x,y)∈Q(G↷X)and on account of Remark 5.2,one has

where

Thus there exist x′,y′∈X and s∈G such that

Combining this with(5.2),we have

The arbitrariness of ε implies that DF(x,y)=0.From this fact it is easy to see that

Thus,(x,y)is proximal.Hence we obtain that

Therefore,we have got that

Q(G↷X)is closed,from Remark 5.2(2),as an intersection of a family of closed subsets is still closed.

Now,we will show that BP(G↷X)is a G-invariant equivalence relation.

Let(x,y)∈BP(G↷X)and let∊>0.By the definition of Banach proximality,it follows that the set F={g∈G:d(gx,gy)<∊}has a Banach density one.It is clear that Fs−1={ts−1∈G:d(tx,ty)<∊}={g∈G:d(gsx,gsy)<∊}.Thus Fs−1has Banach density one,by Lemma 2.3,which implies that(sx,sy)∈BP(G↷X).Thus BP(G↷X)is G-invariant.

Moreover,let(x,y),(y,z)∈BP(G↷X)and let∊>0.Denote that F1={g∈G:d(gx,gy)<}and F2={g∈G:d(gy,gz)<}.Then F1and F2both have Banach density one.It is easy to check that

so,by Lemma 2.3,F has Banach density one,which means that(x,z)∈BP(G↷X).Hence BP(G↷X)is an equivalence relation.This complete the proof of Theorem 1.1. □

AcknowledgementsThe authors are very grateful to Prof.Hanfeng Li for his generous sharing of knowledge and his ideas regarding the topic.The authors would also like to thank the anonymous referee for his/her careful reading and helpful suggestions concerning this paper.