基于DRR及相似性测度的2D-3D医学图像配准算法

2021-06-16麦永锋孙启昌贾鹏飞陈晓军

北京生物医学工程 2021年3期

麦永锋孙启昌贾鹏飞陈晓军,2,3

0 引言

随着医疗影像学的迅速发展，医学图像广泛应用于临床诊断和治疗中。CT(computed tomography)等三维图像数据，由于其直观性，能够显示患者的三维信息，因此有助于医生精确定位病灶位置从而设计缜密的手术计划[1-2]。CT等三维图片数据虽然包含三维空间信息，但不能在术中实时获得。相比较而言，X线图像等二维数据可以在术中通过C形臂获取，但是它缺少三维体数据的空间信息。因此通过二维数据和三维数据结合，若将术中的二维X线图像与术前CT体数据进行配准就可以有效补偿一些空间信息，兼得两者优点[3]。

为了实现准确的二维/三维配准，国内外研究学者提出了不少配准算法，大致分为基于图像特征和基于图像灰度两类[4]。基于特征的方法利用患者身上的标记物或内部固有特征定位。如Wang等[5]在术前通过对人体贴皮肤标志点或打钛钉来实现图像的配准，该方法精确度高，但标志点对人体都有损伤，无法达到微创的要求。苏州大学张建法等[6]通过设计标定靶，并把标定靶安装在C形臂上，将C形臂转换为相机模型进行标定求得3D到2D的映射参数。该方法需要额外设置辅助部件，同时也需要借助反光小球以及红外接收仪等手术导航设备，配准过程复杂。Yu等[7]采用B样条统计形变模型，分别提取二维图像和三维图像的特征，实现2D/3D的非刚性配准，但该方法需要使用一定数量的数据集计算B样条统计模型的参数，且应用到其他部位需要重新训练统计学模型，使用起来比较繁琐。总的来说，基于特征的方法存在对人体伤害较大、需要辅助部件、特征提取步骤繁琐等种种问题，难以满足临床需求，现有研究更倾向基于灰度的配准方法。

基于灰度的配准方法首先采用数字重建放射影像(digital reconstruction radiography，DRR)技术[8-9]将3D图像投影成2D图像，然后选择适当的目标函数测量重建图像与X线图像的相似程度，通过优化求得最佳配准[10-11]。在基于灰度的配准方法中，DRR算法、相似性比对算法以及优化策略的选择均对算法效率、算法精度产生重大影响。根据基于灰度的配准方法的研究思路，Tornai等[12]提出基于GPU渲染DRR图像，该方法能提高DRR图像生成速度，但对配准方法的研究较少。Toth等[13]基于MRI图像和增强X线图像的灰度信息，实现MRI和X线图像在心脏再同步化治疗手术中的配准，但该配准方法仅针对心脏部位的2D/3D配准，难以推广到其他病灶部位。Mu等[14]通过Slab算法提高DRR图像的生成速度来提高配准效率，并使用互信息作为相似性测度，但该方法配准误差较大，缺少不同种类相似性测度的性能比较。陈龙等[10]提出配准过程中采用多分辨率策略和动态改变配准步长加快配准速度，并使用归一化互信息评估DRR图像和X线图像的相似性。该配准系统能在不损失配准精度的情况下提高配准效率，但归一化互信息指标只适用于X线图像与DRR图像存在明显线性依赖关系的理想情况。若X线图像与DRR图像非线性差异显著，归一化互信息相似性测度性能会下降。从现有工作可知，目前基于灰度信息的CT与X线图像配准方法大多采用传统的相似性测度指标，如归一化互相关、梯度差分等。但在实际应用中，由于C形臂X线机型号差异等客观因素影响，X线图像风格往往存在较大差异，传统的相似性测度指标无法适应不同的X线图像风格。

针对上述缺点和不足，本文提出一套完整的基于DRR及相似性测度的2D/3D医学图像配准方法，并对相似性测度方法进行改进，提出融合归一化互信息和梯度差分的相似性测度指标，以适应不同风格的X线图像输入，提高算法的鲁棒性。

1 方法

基于图像灰度的二维/三维配准是一个迭代的过程，主要包括图像插值、空间参数变换、相似性测度和优化策略四大部分。三维CT体积图像与二维X线图像的配准主要步骤如下。

(1) 对于三维CT数据进行预处理插值，同时为了减少配准时间，采用包围盒裁剪三维数据场裁剪出感兴趣的区域(region of interest,ROI)。

(2) 对于X线进行中值滤波预处理，去除噪声。相比于均值滤波，中值滤波能较好地保持边缘的信息，保留图像细节，适用于X线图像。

(3) 给定初始变换参数，对于三维CT数据应用数字重建放射影像生成DRR图像。

(4) 利用多分辨率采样技术对于X线图像和DRR图像采用多分辨率多阶段采样。

(5) 对于DRR图像和X线图像进行相似性测度计算，应用相似性算子实现。

(6) 判断相似性测度是否为极值，若是则配准完成，输出配准矩阵；若不是，采用优化策略变换得到新的参数，转到步骤(3)。

图 1为2D/3D图像配准流程图。

图1 2D/3D图像配准流程

1.1 数字重建放射影像技术

DRR图像的生成是模拟X线射线穿透CT体数据经过衰减吸收后投影到成像平面进行累加的一个过程。对于一个由Nx×Ny×Nz个体素构成的离散模型，在每一个体素内部其密度分布是均匀的，体素值记为ρ(i,j,k)。则该体素的仿真投影数据为

(1)

式中：L为射线路径；l(i,j,k)为射线与体素(i,j,k)的相交长度。

即重建放射计算的实质是射线与体素的遍历求和交问题，而其中最为关键的是求交算法，即确定射线与单个体素的相交长度。本文采用Siddon算法[15]求X线射线与体素的相交长度。图 2为脊柱DRR的效果图。

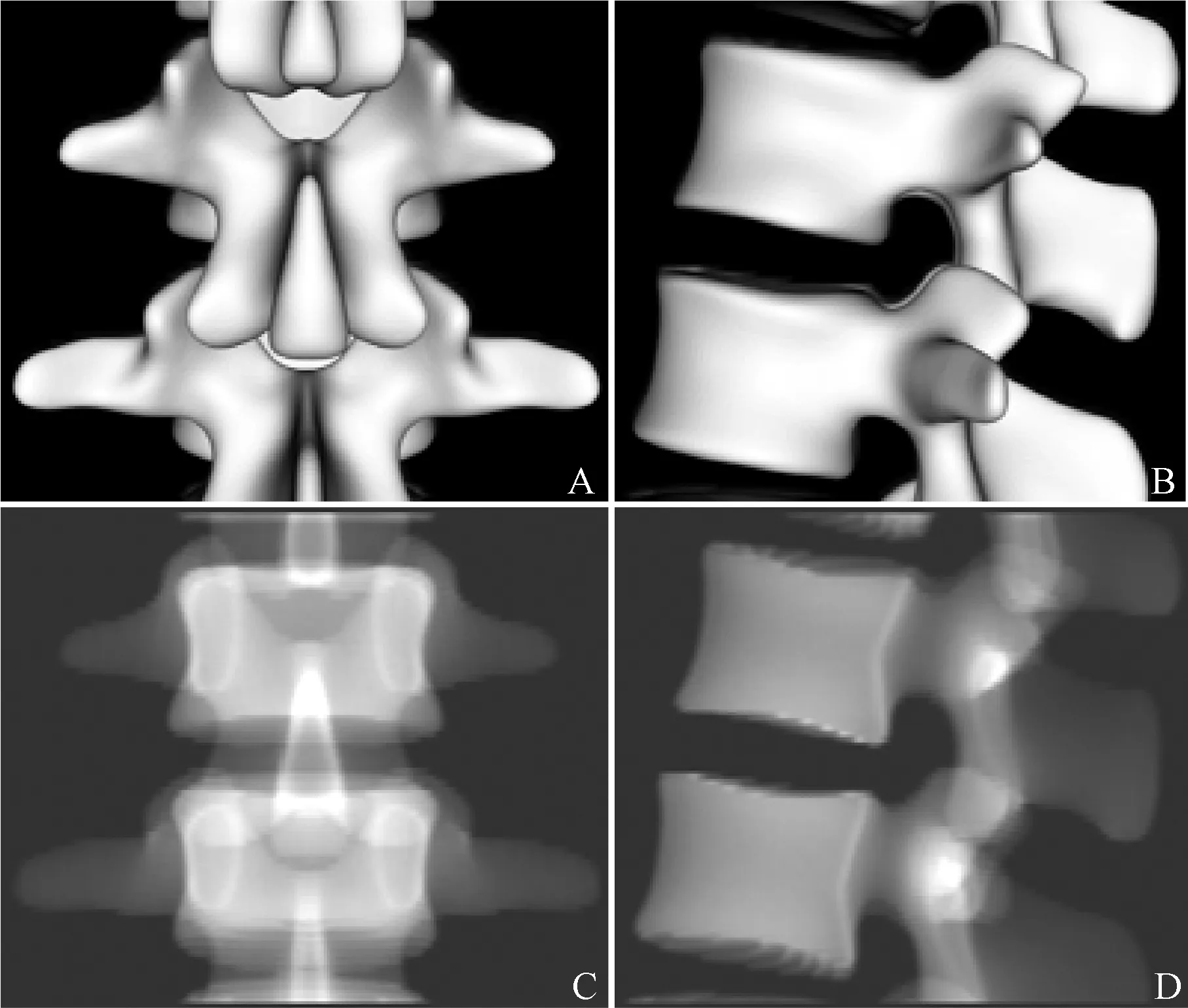
A—0°CT提取模型；B—90°CT提取模型；C—0°DRR图像；D—90°DRR图像

1.2 相似性测度

相似性测度用以表征DRR图像和X线图像的相似或者差异。在2D/3D图像配准算法中，相似性测度常用指标有归一化互相关(normalized cross correlation，NCC)和梯度差分(gradient difference，GD)等[16]。

1.2.1 NCC

NCC相似性测度基于图像灰度信息进行计算，图像I1和图像I2的NCC计算公式如下：

(2)

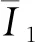
如果一个图像线性依赖于另一个图像，即∀(x,y)∈T:I2(x,y)=aI1(x,y)+b，则NCC值为1(如果a为负，则值为-1)。这就意味着在实际应用中，图像的对比度和亮度的变化不会影响NCC值。在三维CT和二维X线图像配准问题中，DRR图像与X线图像大致存在线性依赖关系，故NCC相似性测度广泛应用于二维/三维配准问题[17-18]。但对于一些风格差别较大的X线图像，基于NCC相似性测度的配准效果会下降。

1.2.2 GD

GD是评估两幅梯度图像的相似性测度，计算公式如下：

(3)

式中：IdiffH、IdiffV分别为水平方向和垂直方向的梯度图像；Ah和Av是常数，一般设置为各自参考图像灰度值的方差；s为缩放因子。

由于梯度差分法使用的是图像的梯度信息，采用梯度差图像作为计算依据，与NCC相似性测度相比，梯度差分法更能适应X线图像和DRR图像的风格差异。但图像噪声对GD指标有一定影响。

1.2.3 NCC和GD相似度测度融合改进算法

为提高配准的鲁棒性，使配准算法更好地适应不同风格的X线图像，本文基于NCC和GD相似性测度指标，提出融合NCC和GD的相似性测度指标，记为归一化互相关-梯度差分(normalized cross correlation-gradient difference，NG)指标。NG指标实质是对NCC和GD进行加权平均。因NG指标融合了NCC和GD的信息，既能发挥NCC在二维/三维配准中评价图像线性依赖关系的优势，又能发挥GD适应不同X线图像风格的优点。

(4)

式中：W1和W2分别为NCC和GD指标的权重。在本文实验中，取W1=W2=0.5。

1.3 优化策略

选择合适的优化策略在二维/三维配准中尤为重要，因为每一次迭代都要重新生成DRR图像，而生成DRR图像的过程比较耗时，必须采取合适策略减少迭代次数提高配准效率。此外，两幅图像之间的相似性是高度非线性的，所以不能使用任何参数来约束配准问题。因此，二维/三维配准问题中的最优化类别是无约束的非线性优化。

术中采集的X线图像和术前三维CT图像通过内部参数ν和外部变换参数μ在空间上相关联。内部参数包括光源到图像的距离，像素大小(px,py)以及2D图像相对于3D图像(cx,cy)的位置组成。外部变换参数通过3个旋转参数rx、ry、rz和3个平移参数tx、ty、tz描述了三维体积相对于二维图像的方向和位置，如图3所示。在2D/3D图像配准中，目标是找到一组参数μ，使X线图像和DRR图像的相似度最高。

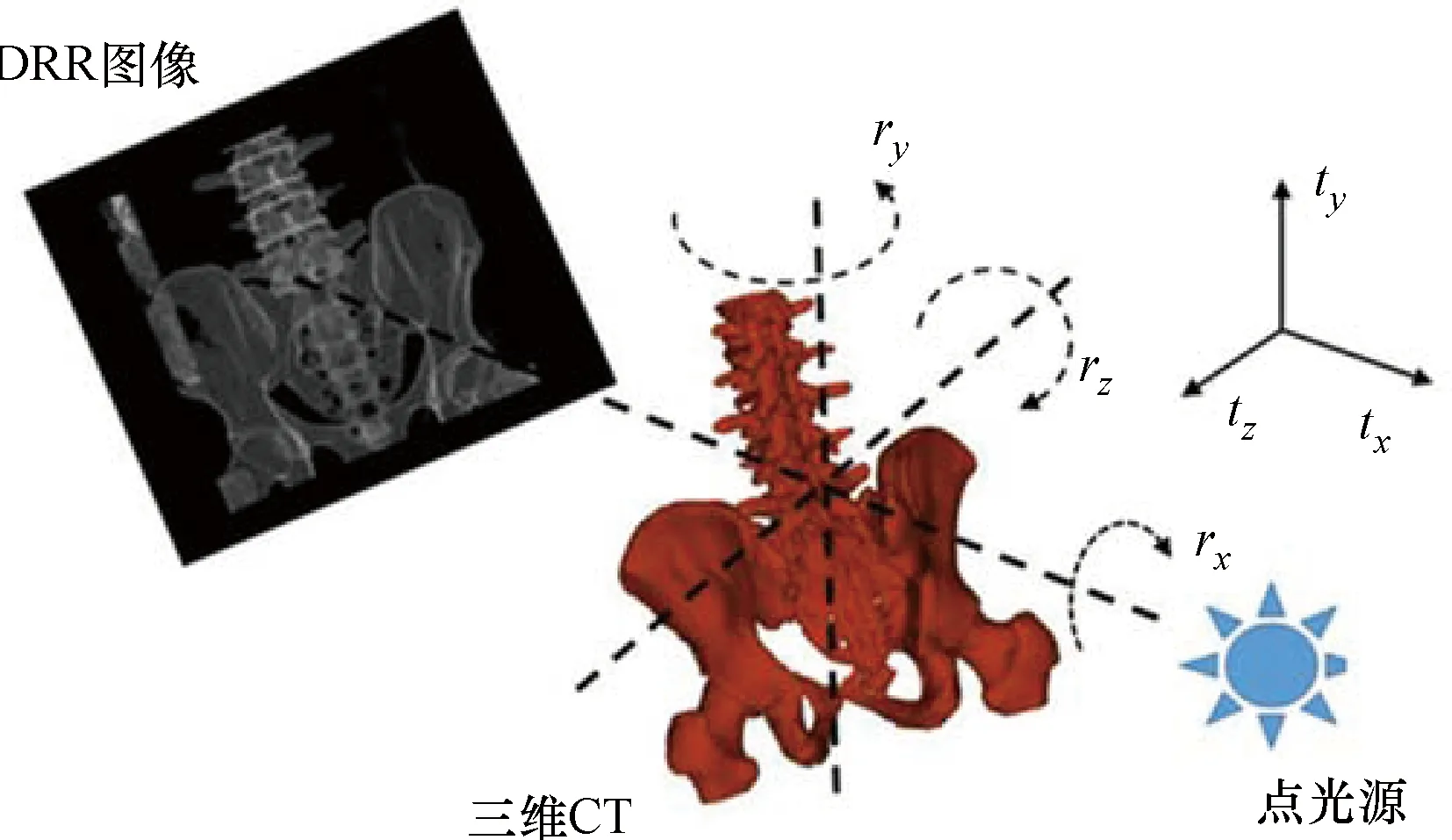
图3 二维/三维配准6个待求参数

配准过程中，将X线图像视为“固定”的，三维CT图像视为“移动”的。2D/3D配准可以表示为：

(5)

式中：NG(μ,IF,IM)为三维模型经过外部参数μ变换后，随参数μ变化的DRR图像与“固定”的X线图像的NG相似性测度值。

非线性优化常见方法有梯度下降法、Powell算法[19]等。Powell算法能够利用共轭方向来加速收敛速度，这对于图像配准特别是基于灰度的配准有很大的好处，能够大大减少优化时间。同时，它不用对目标函数进行求导，只要求目标函数连续，非常适合二维/三维图像配准优化。因此，本文采用Powell算法进行优化。

对于本配准问题，鲍威尔优化算法首先需要构造共轭方向集，构造过程如下。

然后重复下列各步骤，直至函数值不再减少：

(1) 初始位置为P0；

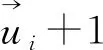
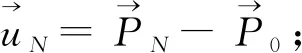
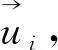
Powell算法优化的思想是在N轮迭代以后，只需沿着N个方向做一遍一维搜索，就可以精确地求出一个二次型的极小值。对于不具有精确二次形式的函数，一轮迭代是不能精确地求出极小值，但经过几轮一次搜索后，也能在适当的时候二次收敛到它的极小值[20]。

得到共轭方向集以后，就开始沿着方向集搜索最小值，计算步骤如下。

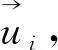
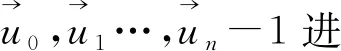
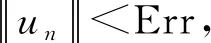
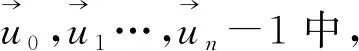
通过以上迭代过程，就能够求出配准的6个参数，得到配准矩阵。

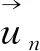
定义

f0≡f(P0)，fN≡f(PN)，fE≡f(2PN-P0)

式中，fE为函数在某“外推”点处的值。该点沿设置的新方向较远，同时定义Δf为本轮迭代中沿某特定方向函数值的最大下降量(其中Δf为一正值)，则做如下判断：若fE≥f0，则保持原方向集不变进入下一轮迭代，在这种情况下，平均方向PN-P0没有任何用处；若2(f0-2fN+fE)[(f0-fN)-Δf]2≥(f0-fE)2Δf，则仍然以原方向集进入下一轮迭代。这是因为沿平均方向PN-P0，函数值的下降在很大成分上并不是由某一个单个方向上的下降；或者沿着PN-P0有一相当大的二阶导数存在，这说明已经很接近极小值的底部。

为进一步加快优化速度，本文通过多分辨率优化策略[22-23]，将配准过程分为粗配准和精配准两个阶段。随着优化的进行，对CT和X线图像进行从低分辨到高分辨率的采样。低分辨下的图像配准为下一级的配准设定一个较好的起始变换参数，既加快了配准进程,又能保证配准的精度不会下降。

2 初步验证及其结果

本文基于QT、VTK (https://www.vtk.org)、ITK (https://itk.org)开源库，开发了一套二维/三维图像配准软件，并把整套配准方法封装其中，软件界面如图4所示。为评估二维/三维配准算法的性能好坏，本文分别采用“黄金标准”判断法和脊柱图像配准的实际应用，定量和定性地评估配准的效果。

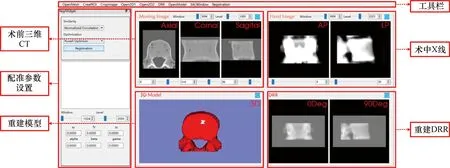
图4 二维/三维图像配准软件

由于现实中无法得到X线图像和待配准CT图像的相对位置关系，直接使用X线图像与CT图像配准无法定量衡量配准的精度。为定量验证所提配准算法的精度，本文采用“黄金标准”判断法，流程如图5所示。“黄金标准”判断法是指在配准过程中，用已知位置的CT生成的DRR图像代替X线图像作为二维输入图像。以该CT位置对应的旋转、平移量为“黄金标准”，该位置对应的DRR图像与三维CT图像进行配准，通过配准得到的结果与已知的“黄金标准”作比对，判断配准系统的好坏。由于X线图像与DRR图像成像的数学原理一致，图片相似性较高，使用“黄金标准”DRR图像代替X线图像也能正确反映系统性能。同时，本文对输入到配准系统的“黄金标准”DRR图像作不同风格处理，以验证该配准系统的鲁棒性。

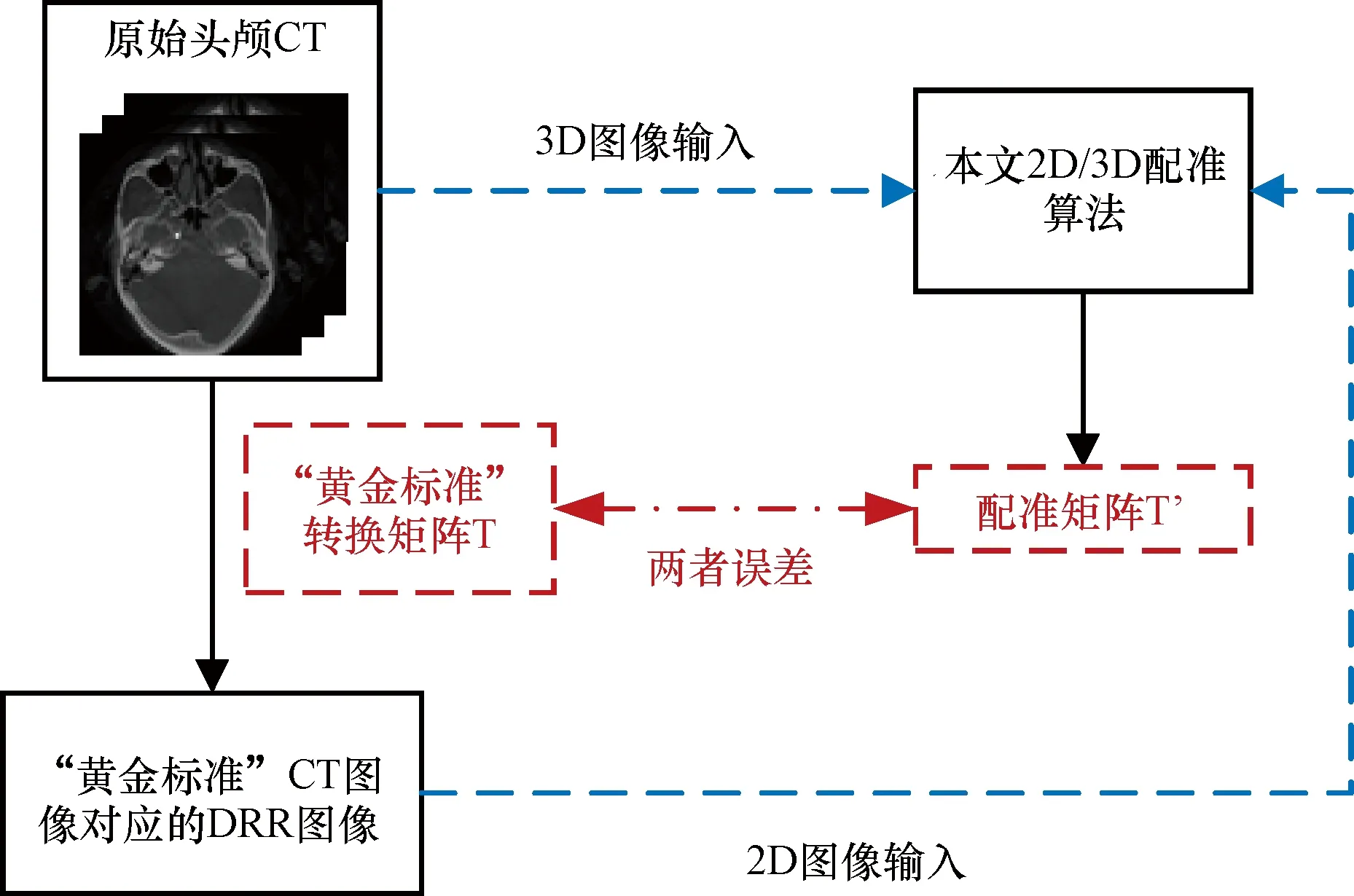
图5 “黄金标准”判断法和CT数据

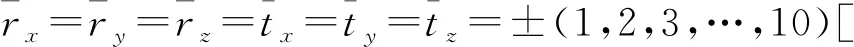
为了综合分析量化配准数据，定义第i(1,2，…，19,20)组数据的角度误差Ei,A和位置误差Ei,P分别为：

(6)

(7)

式中：rx、ry、rz、tx、ty、tz为配准迭代结束后的变换参数。

表1为20组数据的配准结果，20组数据距离平均误差为0.51 mm，角度平均误差为0.40°。从表1可以看出当初始偏移位置越小，配准时间越短。这是因为偏移位置越小，需要重建DRR、重采样和插值的次数就越少，算法内部计算的次数少，计算快，越容易达到最优相似度值。其次，本文的配准算法稳定性较高。对于这20组测试案例，距离误差均小于0.8 mm，角度误差小于0.7°。

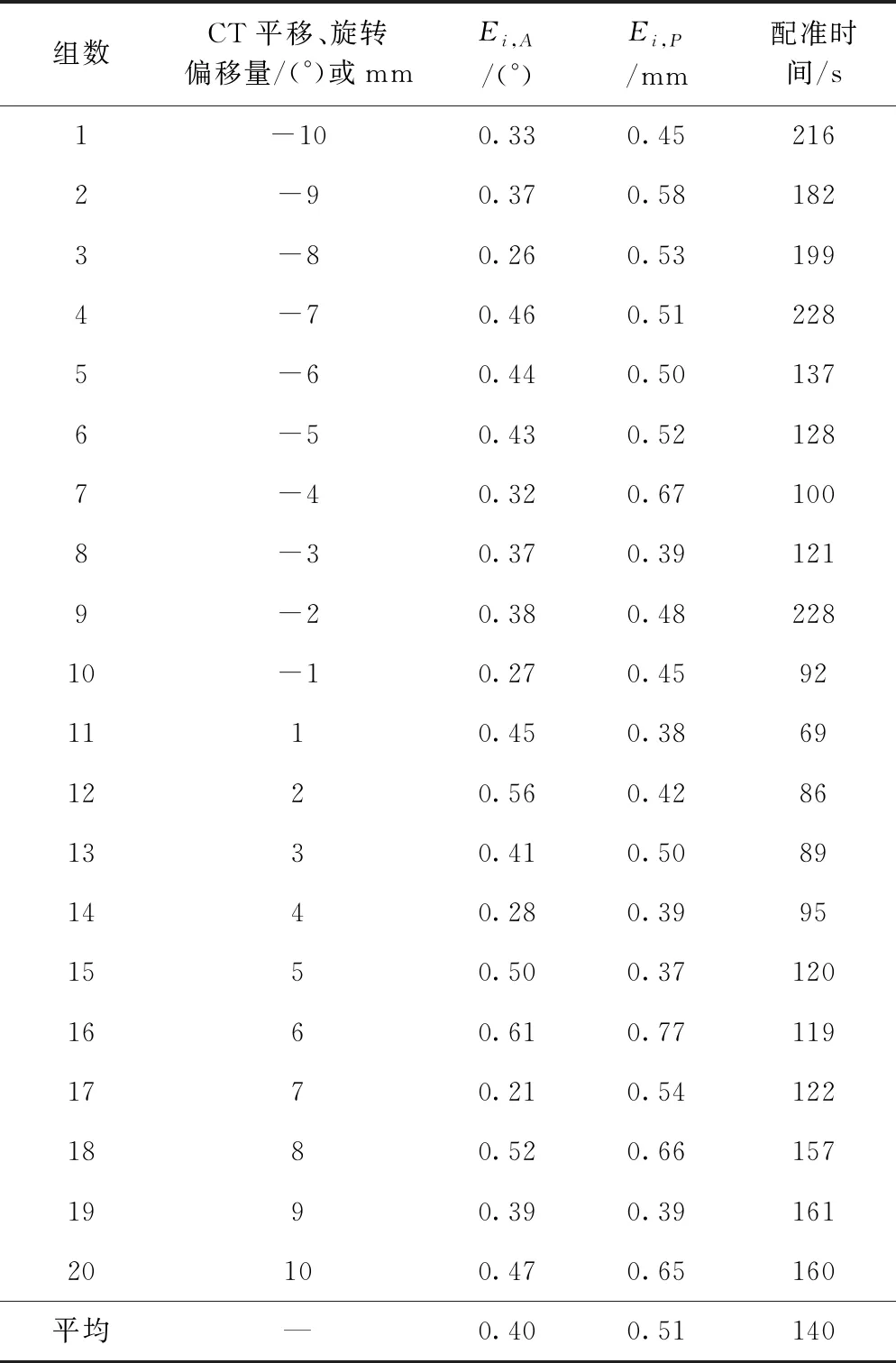
表1 20组数据配准结果

为了验证本文提出的NG相似性测度指标具有更强的鲁棒性，能适应不同风格的X线图像，本文对正侧位“黄金标准”DRR图像分4组作处理。

组Ⅰ：灰度线性调节。正侧位图像亮度增加30%，对比度减小30%。

组Ⅱ：窗宽窗位调节。正侧位图像窗位设置为90，窗宽设置为180。

组Ⅲ：伽马变换。伽马变换标准公式为s=crγ，其中，r为原始图像像素，s为变换后图像的像素。本文取常数项c=1,γ=2。

组Ⅳ：加入高斯白噪声。

处理后的效果如图6所示。第1列是原始DRR生成器生成的正侧位图像，第2～5列分别为原始图像经过组Ⅰ到组Ⅳ处理后生成的具有风格差异性的图像。使用处理后的4组图像配准算法的输入，每组数据分别进行上文描述的20组数据配准。配准的平均距离误差和角度误差如图7和图8所示。使用不同相似性测度进行配准时，5组图像配准误差的组间标准差如表2所示，其中σ(Ei,P)和σ(Ei,A)分别为配准距离和角度误差的组间标准差。

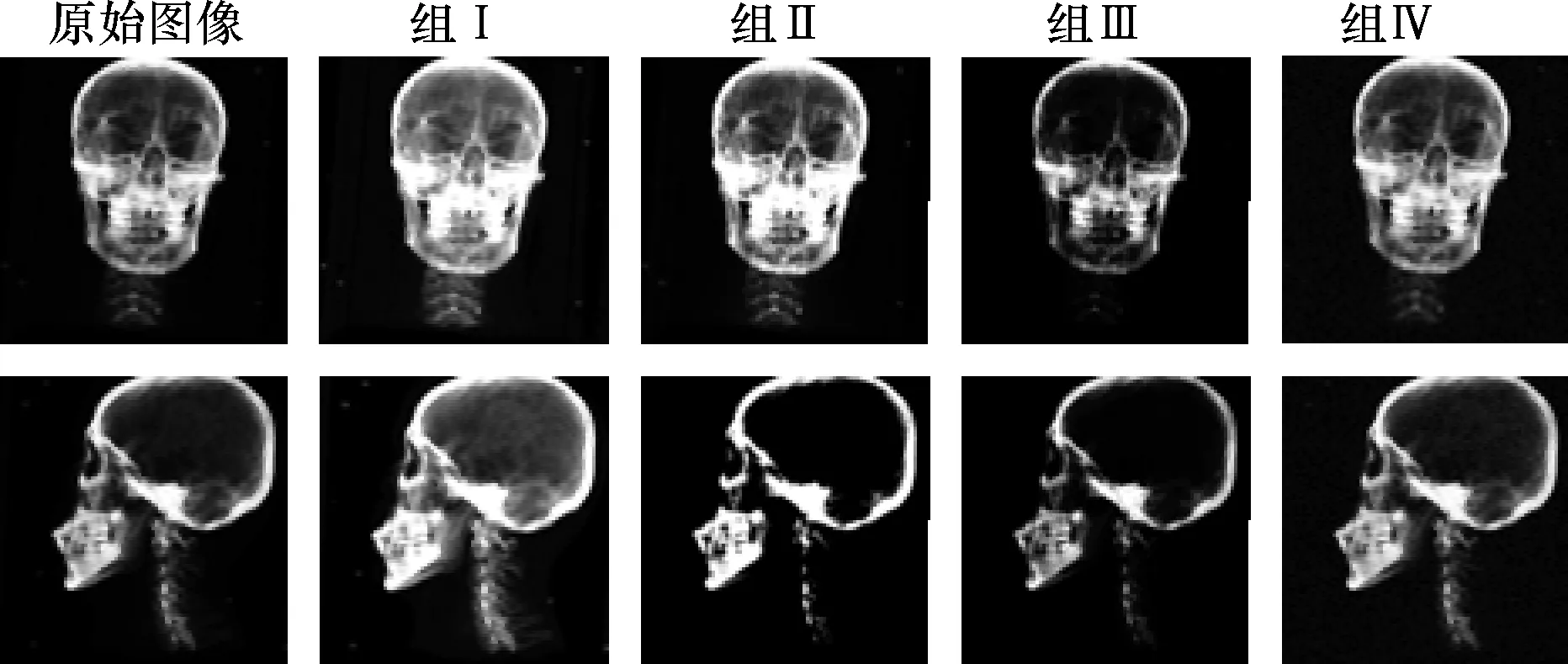
图6 经过不同风格处理的“黄金标准”DRR图像

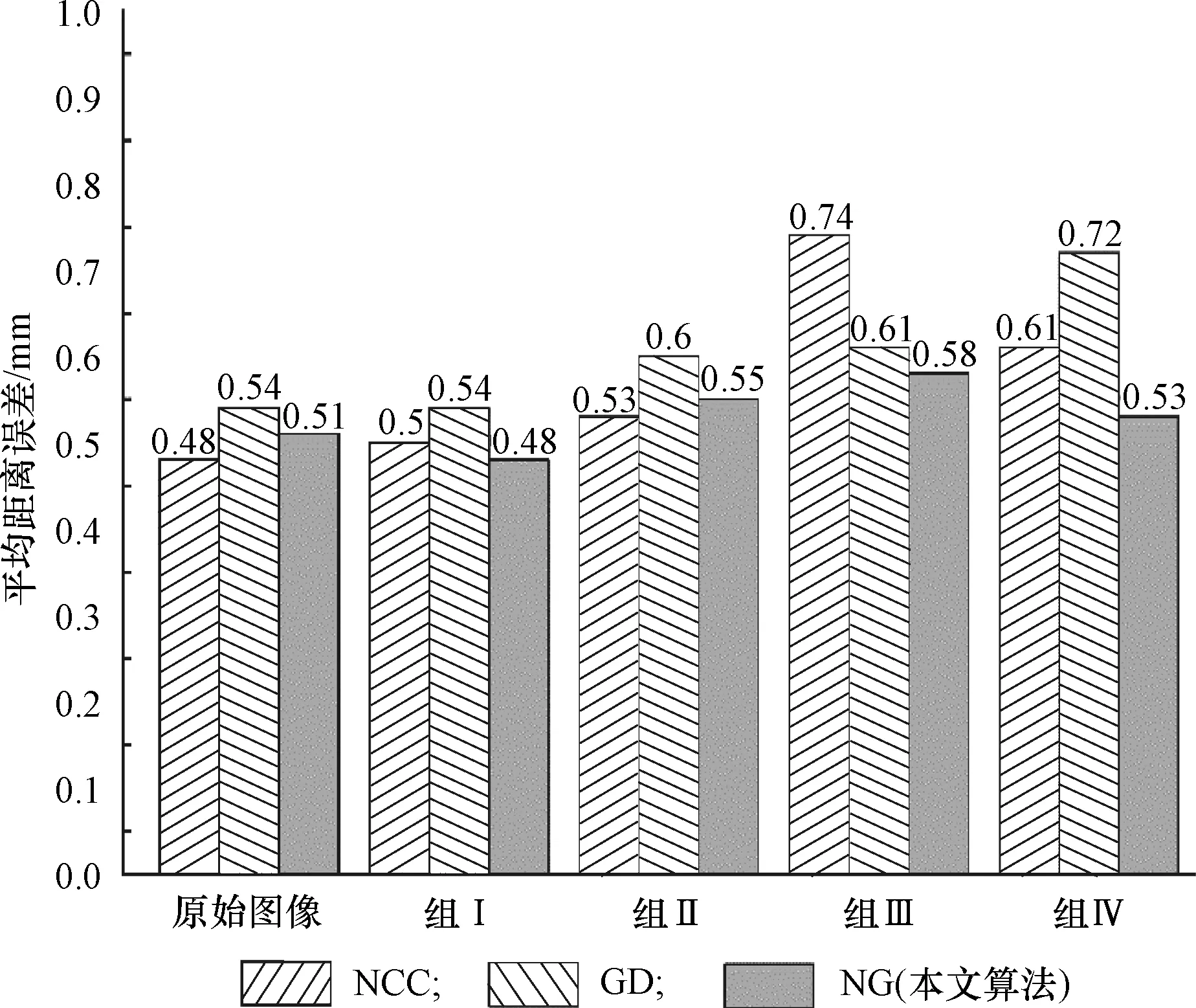
图7 不同风格图像的平均配准距离误差

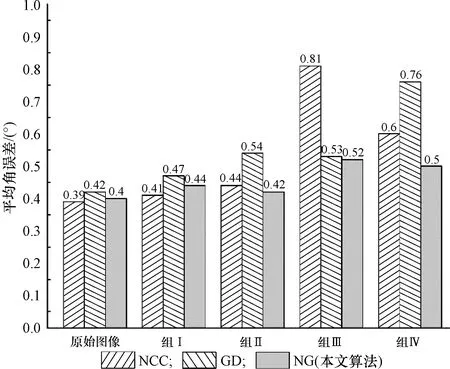
图8 不同风格图像的平均配准角度误差

因为组Ⅰ是在原始DRR图像的基础上作线性变换，只针对亮度和对比度进行调整，所以使用不同的相似性测度进行配准精度都较高。对于组Ⅱ、组Ⅲ和组Ⅳ的配准，由于图像进行了非线性变换，其风格与DRR生成器生成的图像有明显差异。使用NCC相似性测度作配准时，组Ⅲ配准的平均距离误差达到了0.74 mm，角度误差达到了0.81°。如果用GD相似性测度进行配准，则组Ⅳ的配准误差很大。因此，无论是GD还是NCC作为相似性测度指标都存在明显的缺陷，无法适应不同风格的输入。而本文提出的NG相似性测度指标对所有组别的配准效果都比较好，各组别的平均距离误差都在0.58 mm以下，平均角度误差都在0.52°以内，没有因风格差异而导致误差明显增大，说明本文提出的算法能更好地处理与DRR图像风格差别较大的X线图像。从表2数据亦可得知，使用NG指标配准时，距离和角度误差的组间标准差显著小于NCC和GD指标，充分说明使用NG相似性测度指标进行配准稳定性和鲁棒性更高，对不同风格的二维图像输入都有良好效果。由于NG指标融合了NCC和GD的信息，从实验数据可以看出，在多数情况下，使用NG指标进行配准的精度更高。因此，使用NG指标能显著提高二维/三维配准的精确性、稳定性和鲁棒性。

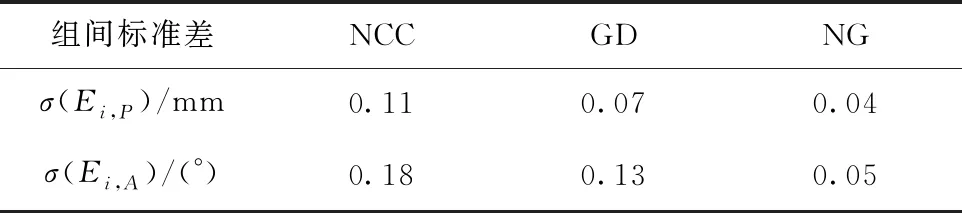
表2 5组图像配准误差的组间标准差

为了验证本配准系统在实际应用中配准CT图像与X线图像效果，本文以第L4节脊柱的CT与X线图像数据进行定性验证。在本实验中，二维输入图像为脊柱X线图像，三维输入图像为脊柱CT图像，CT数据为191×227×16像素，空间分辨率为0.3125 mm×0.3125 mm×2 mm。将其导入到3D Slicer 4.10.2(http：//www.slicer.org/)软件中进行重建得到三维模型(图 9A)。X线数据正位(图 9B)和侧位(图9C)均为200×120像素，空间分辨率均为0.4 mm×0.4 mm。

运用本文配准系统进行配准，正侧位图像配准棋盘效果如图9E和F所示，脊柱配准前后的位置转换如D所示。从配准棋盘效果图可以看出，虽然X线图像和DRR图像在图像表现上有区别，但生成的DRR图像和原始X线图像能够较好地对应起来。因此，基于NG相似性测度指标的配准系统可以有效解决CT和X线图像配准问题。

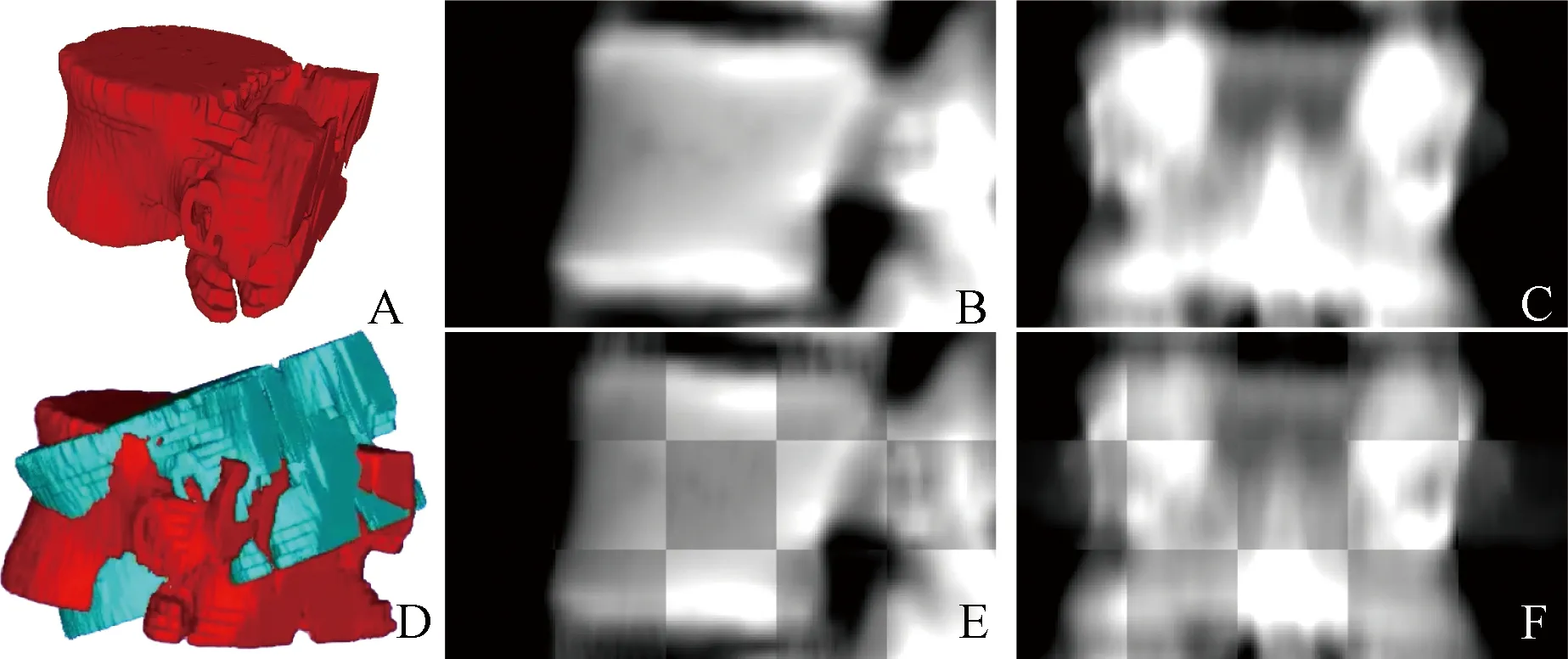
A—脊柱CT重建三维模型；B—正位X线图像；C—侧位X线图像；D—配准前后三维模型的位置；E—正位片配准效果；F—侧位片配准效果

从以上定性和定量实验可见，本配准系统配准精度较高，算法鲁棒性和稳定性较好，能适应不同风格的二维图像输入。

3 讨论

由于X线和CT是不同维数的，所以本文采用数字重建放射影像技术，模拟X线射线的穿透过程，将三维CT数据转换成模拟X线数据，从而将CT和X线图像的配准问题转化为DRR图和X线图的配准问题。然后使用Powell优化算法迭代求解最优的CT位置转换矩阵，使DRR图像和X线图像相似度最大。由于求解的CT配准矩阵是刚性变换矩阵，且2D/3D图像配准算法常用于骨科手术等需要刚性组织配准的场景，本文不考虑软组织变形配准情况。

衡量DRR图像和X线图像的相似度是2D/3D图像配准的关键步骤。传统方法常采用NCC或GD指标作为相似性测度的标准。NCC的优点是对于存在线性依赖关系的两幅图像，图像的对比度和亮度的变化不会影响NCC值，但X线图像与DRR图像的非线性差异会降低NCC指标的性能。在本文实验中可以看到，由于伽马变换是非线性变换，若对“黄金标准”DRR图像作伽马变换，使用NCC配准算法的配准误差会增大。GD指标的优点是更能适应不同风格的X线图像，但图像噪声对GD指标比较敏感，影响配准精度。为了弥补NCC和GD指标的缺点，本文创新性地对NCC和GD进行加权平均，提出NG指标。因为NG指标融合了NCC和GD的信息，所以既能发挥前者在二维/三维配准中评价图像线性依赖关系的优势，又能发挥后者能适应不同X线图像风格的优点。

本文分别通过“黄金标准”判定法和实际脊柱应用的案例，定量和定性地评估NG指标的配准性能。“黄金标准”判断法使用“黄金标准”DRR图像作为二维输入图像，解决了实际应用中CT和X线图像配准难以定量衡量配准精度的问题。因为DRR图像是X线图像成像过程的数学模拟，具有较高相似性，所以“黄金标准”DRR图像代替X线图像作为输入也能正确反映CT、X线图像配准系统的精度。“黄金标准”判断法的实验显示，本文提出的基于NG显示性测度指标的配准系统配准人体头颅图像数据的平均距离误差为0.51 mm，角度误差为0.40°，精度较高。其次，NG指标最大的优势在于能够适应不同风格的图像输入。与NCC和GD相比，使用NG相似性测度指标的配准算法在输入不同风格类型的图像时，配准结果标准差最小，说明其性能最稳定，鲁棒性最高。

在实际应用中，本文通过脊柱CT和X线图像的配准实验，证明了虽然脊柱DRR图像和X线图像风格存在较大差异，但是基于NG相似性测度的配准系统仍可有效解决CT和X线图像配准问题。