基于组合模型的风电机组轮毂载荷预测方法研究

2021-06-16廖圣瑄马晓明韩中合贾海坤

中国测试 2021年5期

廖圣瑄，马晓明，韩中合，贾海坤

（1.华北电力大学能源动力与机械工程学院，河北保定 071003; 2.中国电力科学研究院有限公司，北京 100192）

0 引言

近年来，随着风电行业的发展，风电开发的重心由陆地向海上转移，风电场建造规模不断扩大，风电机组运行过程中的安全性问题也越发严重。风电机组运行过程中对载荷进行评估可以保障机组运行的安全性和经济性[1]。为此有必要对风电机组主要部位的受载情况进行分析，以保障机组正常运行。风电机组载荷主要来自于重力和空气动力等，载荷状况会对风电机组运行造成一定影响。目前对风电机组正常运行的载荷情况进行分析时，通常使用实验测试或者使用FAST和GH bladed等载荷计算软件进行仿真分析[2]。以GH bladed为例，该软件计算载荷时主要通过实验日的环境参数和机组参数建立动态数学模型，对风机组正常运行的载荷情况进行仿真分析[3]，实际计算过程中存在计算量大、耗时长的问题，不适用于短期风电机组载荷评估。周士栋等[4]通过建立BP神经网络对风电机组部分载荷进行预测；秦斌等[5]通过建立极限学习机对风电机组叶根载荷进行辨识。然而单一模型的神经网络在预测过程中往往存在陷入局部最优解和误差较大的问题。鉴于实测和仿真过程中存在成本高、耗时长的问题，本文提出了基于组合算法的风电机组轮毂载荷预测方法，在机组轮毂载荷预测时将单一神经网络进行优化，使用遗传算法[6]优化BP神经网络[7]，使用粒子群算法[8]优化极限学习机[9]，再使用定权值输入[10]和GRNN[11]融合的方式分别将上述两个模型组合，建立新的模型进行载荷预测。随后以某3.4 MW海上风电机组为例，按照IEC标准对机组载荷进行实测，利用实测数据基于神经网络原理建立了GA-BP、PSO-ELM、BP-ELM-GRNN模型对轮毂载荷进行预测。研究结果可为风电机组轮毂载荷预测提供参考。

1 轮毂载荷预测组合模型

1.1 遗传算法优化的BP神经网络建模

BP神经网络是一种多层前馈网络，目前在数据预测领域运用十分广泛。训练BP神经网络时需不断调整网络的权值和阈值，其隐含层层数一般按经验取值，隐含层神经元个数计算公式如下：

式中：h——隐含层神经元个数；

n——输入层数；

m——输出层数；

a——随机取0～10内的常数。

本文在训练网络时选取最大训练次数为1 000次，目标误差设置为0.001，学习效率设置为0.1。在选用训练次数时，比较一般训练次数为500次和最大训练次数为1 000次时的相对误差均值和决定系数如表1所示。由表可知，选用最大训练次数为1 000时精确度更高。

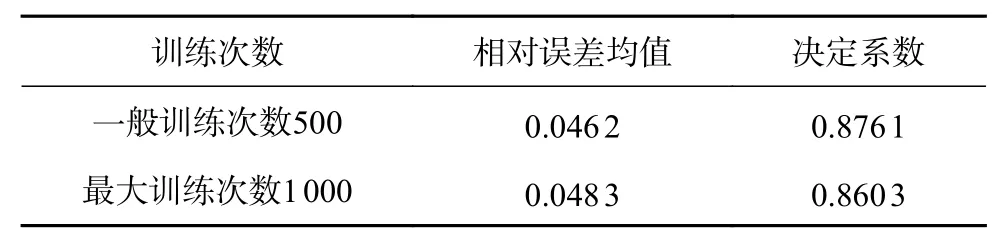
表1 不同训练次数下的误差对比

遗传算法（genetic algorithm，GA）按照自然选择规律进行，通过选择、交叉、变异步骤逐次进行筛选，以达到最优适应度。遗传算法迭代计算过程中，具有更优适应度的种群取代原有种群，多次更新种群以达到目标解。

遗传算法对BP神经网络进行优化的过程中主要通过遗传算法对BP神经网络的初始权值和阈值进行修正。修正时将风电机组的实测载荷与神经网络的预测载荷之间的误差作为遗传算法的适应度，选取15次种群迭代后误差最小值对应的权值和阈值代入BP神经网络。X方向上弯矩在不同隐含层神经元个数时对应的适应度曲线如图1所示，图1中各隐含层神经元个数不同进化代数对应的适应度为进行5次试验计算后所取的平均值。由图可以看出，在进化代数为15时曲线逐渐平缓，每次迭代进化需要6～10 min，且迭代时间随着输入数据增加而增加，选取过多的种群代数时增加迭代次数会导致计算冗长。

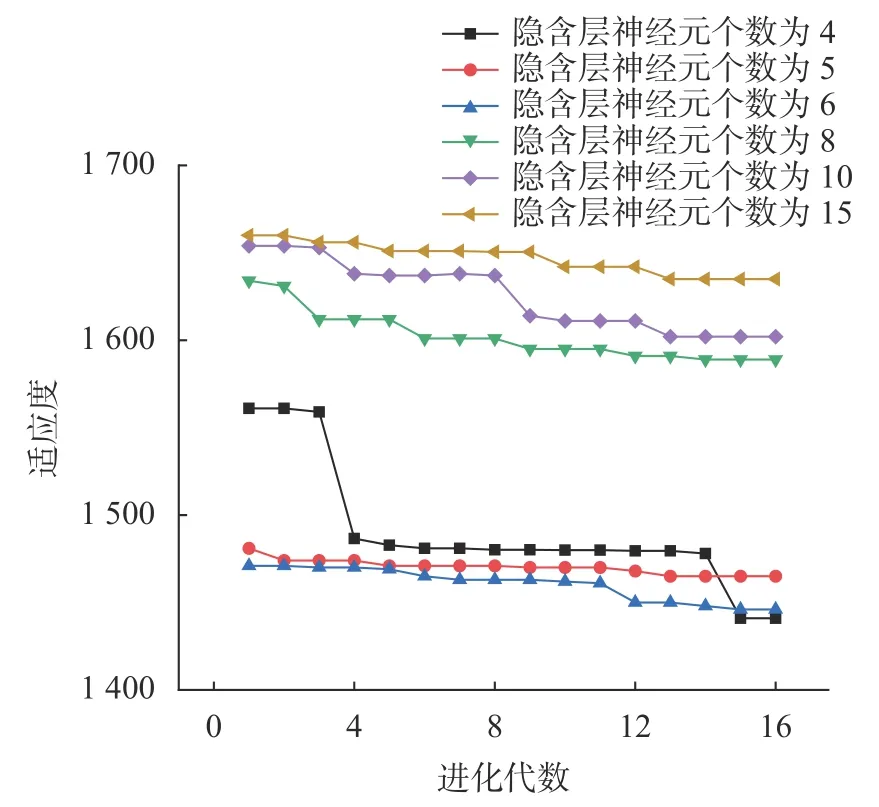
图1 不同隐含层节点适应度曲线

相比于单一BP神经网络而言，利用GA优化后的网络在风电机组轮毂载荷预测时精准性更高。本文在参数设计时遗传算法选择进化代数为15，种群规模为70，交叉概率为0.75，变异概率为0.05。GA-BP模型训练网络时选取最大训练次数为1 000次，目标误差设置为0.001，学习效率设置为0.1。GA-BP预测模型计算流程见图2。

图2 GA-BP模型流程

1.2 粒子群算法优化的极限学习机

极限学习机（extreme learning machines，ELM）相比于BP神经网络只有一层隐含层，在设定参数时随机设定两层之间的权值以及隐含层的阈值，与BP神经网络相比计算过程更快，只需要设置隐含层神经元个数。极限学习机相比于支持向量机而言误差相仿，但极限学习机建模更简单，计算速度更快。

粒子群算法（particle swarm optimization，PSO）最早起源于模拟自然界中鸟群捕食的过程。该算法通过迭代计算逐渐逼近最优解，在迭代过程中，粒子不断更新自身速度和位置，朝着自身最优解和种群最优解接近。粒子群算法进行中粒子更新后的速度 Vid和位置 Xid如下：

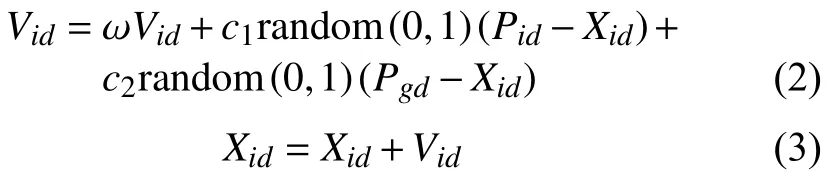
其中c1、c2为学习因子；为惯性因子，通过调整的取值对全局网络进行修正；Pid为第i个变量的d维位置；Pgd为全局最优解的d维位置；random（0,1）为0～1之间的任意数。

本文使用粒子群算法（PSO）优化极限学习机（ELM）时，优化其初始输入的权值和阈值。PSO优化ELM的过程中，先初始化粒子群算法的学习因子、惯性因子、进化代数等参数，再将风电机组轮毂的实际载荷与预测载荷之间的均方误差作为粒子群算法的适应度进行迭代寻优。X方向上弯矩不同学习因子对应的适应度曲线如图3所示，其中各学习因子不同进化代数所对应的适应度为进行5次试验所取的平均值。

图3 不同学习因子适应度曲线

优化过程中每个粒子需要将其当前的适应度与自身最优适应度、种群最优适应度进行对比，不断更新自身位置。本文计算时设置进化代数为200，种群规模为80，初始隐层神经元个数为40，取c1=c2=2.05，PSO迭代寻优后将取得的各层之间的权值和初始隐层的阈值代入ELM中重塑网络进行建模预测。PSO-ELM预测模型计算流程见图4。

图4 PSO-ELM模型流程图

1.3 定权值组合模型

在风电机组载荷预测过程中，由于不同预测模型网络结构不同、预测方式有所差异，部分预测值与实测值误差较大，对此提出建立定权值预测模型。定权值预测模型结合多个模型进行组合预测，每个模型所占权重为固定值，模型之间相互组合以补偿彼此误差。组合模型公式如下：

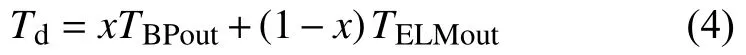
式中：Td——定权组合模型预测结果，N；

TBPout——优化后BP模型预测值，N；

TELMout——优化后ELM模型预测值，N；

x——固定权值。

1.4 广义回归融合模型

在组合模型预测过程中还可以采用神经网络融合的方法，采用广义回归神经网（general regression neural network，GRNN）对BP神经网络和极限学习机进行融合。相比于传统径向基神经网络而言，GRNN同样通过非线性回归分析进行建模，但其映射能力和学习效率都要优于RBF。相比于传统神经网络而言，GRNN没有隐含层到输出层这个环节，而是引入了模式层和求和层，简化结构，加快了运算速度。GRNN函数求和层与输出值的维数有关，其模式层传递函数fi如下：

式中：σ——光滑因子；

Y——输入值；

Yi——第i个神经元的学习样本。

本文利用广义回归神经网络对遗传算法优化后的BP神经网络和粒子群算法优化后的极限学习机进行融合时，首先将从风电机组获取的原始实验数据进行处理，得到12 360组有效数据，将其分为三部分，分别有11 000组、1 260组、100组数据。将第一部分11 000组数据作为训练集1，其中的轮毂风速等参数作为输入集1，轮毂载荷作为输出集1，分别代入GA-BP和PSO-ELM网络中进行训练。将第二部分1 260组数据和第三部分100组数据作为测试集1，代入训练完成后的BP网络和ELM中进行预测，分别保存其载荷预测值。将建立好的GA-BP和PSO-ELM模型中预测输出的第二部分和第三部分载荷预测结果作为新的样本，代入GRNN中作为输入集2，仍然选择其机组实测载荷作为输出集2。对于新建立的GRNN模型，将第二部分各网络预测结果和实测载荷作为训练集2，将第三部分各项数据作为测试集2进行训练。训练完成后的BP-ELM-GRNN组合模型用于风电机组轮毂载荷预测时误差相对较低。

风电机组通过实验获得的输入参数维数不定，将所得参数代入组合模型中，经过GA-BP和PSOELM初步处理后的一次预测结果成为新的二维参数。将其代入GRNN模型中进行预测可以降低输入维数。GRNN用于融合神经网络过程见图5。

图5 GRNN融合神经网络过程

本文采用相对误差均值Er1，绝对误差百分比Er2和决定系数r2对模型的误差进行评测。其计算公式如下：

式中：n——预测轮毂载荷个数；

ei——各点预测误差绝对值；

Ri——第i个点的实际测试值；

Ti——载荷预测模型的预测值；

Ti,f——模型拟合值；

2 工程概况

选取某3.4 MW海上风电机组进行载荷实测，其轮毂高度为95 m，额定风速为10.2 m/s，叶片长度为76.2 m，机组设计按照IEC61400-1-2005规范进行。本文建立轮毂旋转主轴坐标系进行预测，选取坐标系原点位于轮毂中心，坐标系随着风轮一起旋转，坐标系如图6所示。图6中XR，YR,ZR为坐标轴，MiR为i方向上的弯矩，FiR为i方向上的受力。本文研究来自该风电机组正常发电工况下连续运行10 min所得到的风机参数和载荷状况，剔除异常值和缺失值后保留12 460组数据用于评估风电机组轮毂短期受载情况。本次实验采用SCADA系统对风电机组轮毂参数进行收集，将轮毂转速传感器、偏航角传感器等数据采集装置布置在机组相应部位。对于风速等环境参数，采用气象数据采集系统进行收集。

图6 风电机组轮毂旋转主轴坐标系

为了得到较为精准的载荷预估模型，本文将轮毂风速、偏航偏差等基本参数现场实测数据与轮毂载荷进行关联性分析后，选取合适的输入集建立模型，将取自机组的参数设为变量X，轮毂载荷设为变量Y。目前常用的关联性分析方法主要是皮尔逊相关系数法和斯皮尔曼相关系数法。本文计算了各项风机参数与载荷间的皮尔逊相关系数，其计算公式如下：

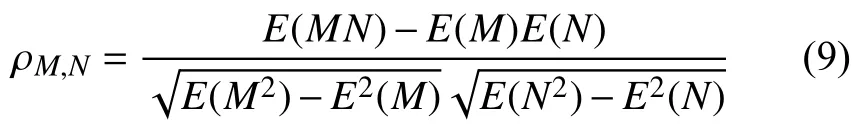
其中E为数学期望。

在统计学中，一般通过相关系数来形容两变量之间的相关程度，皮尔逊系数越高，相关性越强，当皮尔逊系数在0.2以下时，一般认为两组数据间不相关。风电机组主要参数相关于载荷的皮尔逊系数如表2所示。分析表中数据，选取关联度较高的系数进行建模，本文选取轮毂风速、转子转速和平均俯仰角作为输入集，MXR作为输出集进行建模。选取轮毂风速和平均俯仰角作为输入集，FXR作为输出集建立模型。

表2 轮毂载荷的皮尔逊相关系数

3 结果分析

以轮毂载荷X方向上的弯矩MX建模预测时，其GA-BP、PSO-ELM、BP-ELM-GRNN预测模型的预测值与实际值对比如图7～图9所示。通过BPELM-GRNN建模预测轮毂载荷X方向上的受力FX与实际值对比如图10所示。图11～图14为各类模型用于载荷预测时预测结果与实测值之间的残差图。

图7 GA-BP预测弯矩与实测值对比

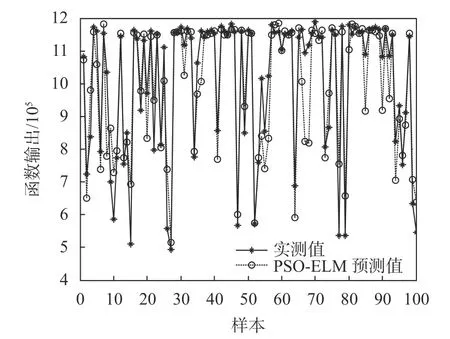
图8 PSO-ELM预测弯矩与实测值对比

图9 GRNN预测弯矩与实测值对比

图10 GRNN预测受力与实测值对比

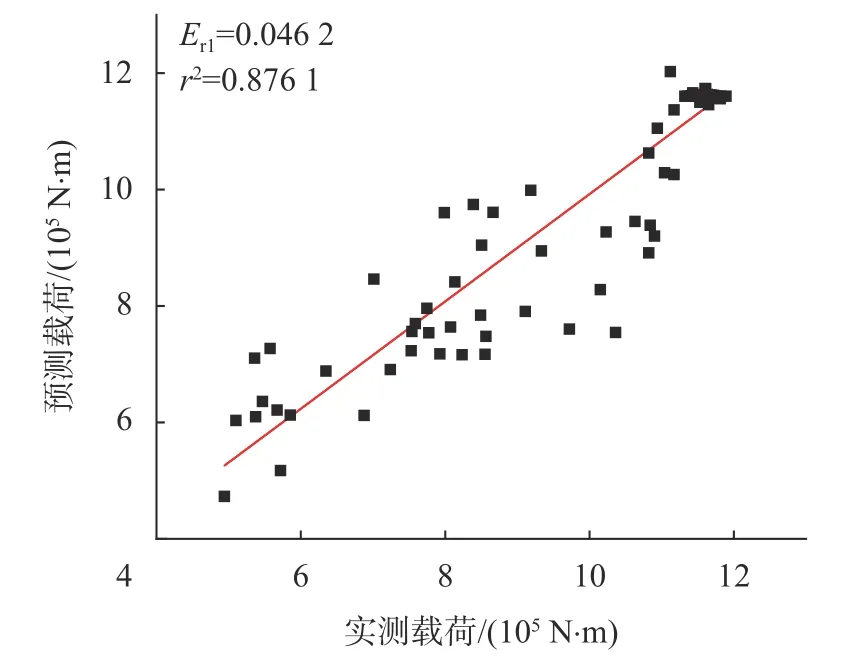
图11 风电机组轮毂旋转主轴坐标系

图12 PSO-ELM预测弯矩残差图

图13 GRNN预测弯矩残差图

图14 GRNN预测受力残差图

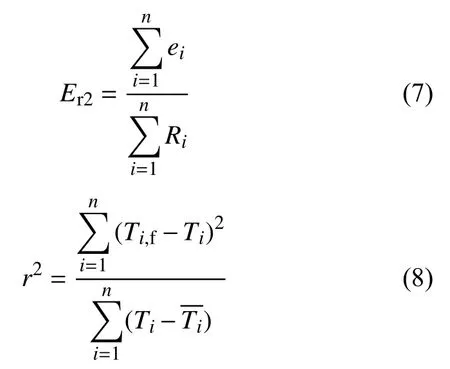
由图7～图9可以看出，风电机组轮毂X方向上的弯矩在较大时，各学习器预测结果基本与真实值相同。对比各图发现单一预测模型在预测过程中相比于优化后的模型，由于其初始权值和阈值未达到最优，预测误差相对较大。同时单一预测模型在网络建立过程中可能陷入局部最优解，影响实验结果。由图11～图14的残差图可以看出，使用各类模型进行预测时的拟合效果较好，用于机组载荷预测的精确度较高。由图7～图14可以看出，采用GRNN对BP、ELM组合可解决单一预测机在预测过程中出现的问题，达到很好的拟合效果。BP、ELM和GRNN都属于强学习器，其预测性能整体而言准确性较高。各类学习器在风电机组轮毂载荷预测过程中误差都比较小，在风电机组早期载荷评价过程中使用可以达到目标精度。通过神经网络融合的方式在一定程度上改善了单个学习器的局限性，提高了预测的准确性。各类学习器预测误差和真实度如表3所示。

表3 不同算法预测结果

由表可知，BP-ELM-GRNN组合模型训练风电机组轮毂载荷效果相比于单个网络而言，误差有所减小。采用GRNN对遗传算法优化后的BP神经网络和粒子群算法优化后的极限学习机进行融合后预测精度得到提高，轮毂弯矩MX的相对误差均值降低到0.044 4，决定系数r2提高到0.879 6，轮毂受力FX的相对误差均值降低为0.048 3，决定系数r2达到0.801 7。定权值组合模型模拟效果与GRNN组合算法预测结果相差不大，同样起到优化单一预测模型的效果。由此可以看出，使用神经网络组合模型可在一定程度上提高风电机组轮毂载荷状况预测精度。