基于机器学习回归模型的房价预测研究

宋尧

（北京十一学校，北京，100039）

1 研究背景

随着第四次工业革命浪潮的来临，一大批科技前沿技术逐渐兴起，人工智能、大数据、5G、物联网等技术不断渗透到各个领域，给各行各业带来巨大的改变。而随着技术的飞速发展，我们的衣食住行正在悄然变化，在追求精神满足的情况下，人们正在不断完善自身的生活条件。房子是每个家庭的必需品，在购买房子时人们总是希望用较低的价格买到理想的房子，然而随着市场的变化，房价时高时低，大众很难捕捉到很好的购房时机，因此房价预测就成为人们普遍关心的事情。很多学者在该领域进行了深入研究，有的通过引入数学模型，结合数据分析来预测房价的走势；有的通过市场分析，结合国家宏观政策调控等，来预测房价的变化趋势。

本文着重从数学模型角度来探究房价变化的影响因素，以波士顿的房价数据为着手点，通过引入随机森林[1]回归模型和全连接回归模型，来预测该市的其他房屋价格，进而帮助大众了解房价变化的真正影响因素。

2 研究方法

本章将要对研究过程中遇到的一些方法做相关介绍，包含随机森林(RandomForest)和全连接模型介绍，旨在从理论基础上对工作做基础调研。

■2.1 算法简介

随机森林采用了多个弱学习器组合形成了强学习器，组合采用了bagging的方式，最终将多个弱学习器计算的结果采用投票或者加权平均的方式得到最终结果，这种方法能够较好的降低方差，使整体结果泛化性较好[3]。

2.1.1 算法思想

由于常见的简单机器学习方法例如决策树，支持向量机都可以在一定程度上达到预测的目的，但是在某些数据上预测效果不能够保证，所以可以在限定场景内将这类的简单机器学习方法成为弱学习器，弱学习器具有一定准确性，而且多个弱学习器之间关注点不同，是包含有差异性的。

一般将弱学习器采用bagging[5]或者boosting[6]的方式集成学习，其中随机森林就是采用bagging的方式合并。Bagging是并行式集成学习方法的代表，它的基本流程是，采用自助采样法，得到多个基学习器，其中分类任务采用简单投票法，而回归任务采用简单平均法。

随机森林是bagging集成算法的一种，随机森林的弱分类器采用决策树，并且在训练过程中加入了随机属性,也就是说先抽选k个属性，然后选择最佳属性。加入了属性扰动，这使得最终的模型泛化性较强。

2.1.2 RandomForest模型介绍

本文中采用的随机森林模型采用的是决策树[4]作为基础模型，而且由于本文所做的工作为预测房价，所以属于回归模型，最终在多个弱模型训练时，采用的是多个分类器的简单平均作为最终的结果。本文共采用了500棵决策树聚集成为随机森林模型。而且由于数据量不足，训练时采用了15折的策略。

■2.2 全连接算法简介

在遇到使用机器学习难以解决的问题，深度学习可以较好拟合数据分布，例如图像识别，翻译等技术，现在大都是由深度学习完成的。本文将要使用全连接方式来对数据做回归训练，旨在探索深度学习的优势。全连接算法即使用神经元的连接并加上非线性激活函数来拟合最终数据。

2.2.1 算法思想

在深度学习中，每一个基本计算单位被称为神经元，在满足一定条件下，神经元将会把自身携带的信息传递给下游，这个过程叫做信息传输。在全连接中，神经元是按照分层的方式做信息传输的，首先从基本数据中将信息传递给第一层神经元，神经元经过信息加工处理后，结果将进入激活函数，然后从激活函数中得到最终信息值，这个信息值将会把结果发布到下一层的全部神经元中，下一层神经元再次处理并向下游传递信息。在训练过程中，采用反向传播的方式来对每一个神经元的参数做调整，经过训练后，将会得到多层的神经元参数，预测时便可以根据已经训练完成的神经元参数来对数据做分类或回归预测。

2.2.2 本项目模型介绍

在本项目中，采用了四层全连接层，还有一层为输出层，分别的维度为[特征维度,256],[256,128],[128,128],[128,1]，训练的损失函数采用了均方误差，优化器采用了rmsprop。在每一层中间采用了dropout[7]率为0.4，这个策略能够一定程度上缓解模型的过拟合，每一层的激活函数采用了Relu[2]，激活函数在神经元输出值为正时信息不会衰减，能够有效的将结果传递给下游，隐藏层中采用了L2正则化，这个策略同样能够减缓模型过拟合。

3 实验及结果

本章将要介绍整个实验过程，包括数据预处理过程，随机森林实验过程和全连接的实验过程，以及最终两个模型的实验效果。

■3.1 实验过程

3.1.1 数据预处理

3.1.1.1 数据获取

我们采用Python中的Pandas来加载数据，并做数据展示，训练数据展示如表1所示。

表1中每一列表示的是房屋的属性或者价格，共有79列；而每一行代表一个房屋的相关数据。在对房价价格进行数据描述时，我们发现其大致符合高斯分布[5]，所以在此进行了数据的平滑处理，最终得到训练集的特征大小为1460×79，其中房屋数目为1460，特征数目为79，另外还有一列对应的房屋价格label的数据。

3.1.1.2 数据处理

本文首先对预测结果(房屋价格)取了对数结果，使价格区间大致符合正态分布。具体如图1所示。

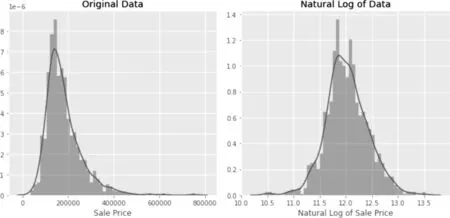
图1 房屋价格取对数

然后对于缺失的列查看了其有效性，如果某些列缺失数据较多且与价格之间无明显关联，本文中将会把这类的特征去除。

接着，对所有类型参数采用独热编码方式，对所有数值参数采用归一化处理，最终得到了训练和测试的特征数据。

3.1.2 训练模型

此次研究采用了两种不同的模型，形成了两种方案。第一种方案使用了随机森林模型，将相关特征作为输入，目的是使用多棵决策树来拟合最终房价；第二种方案为采用深度学习全连接来做回归预测，目的在于尝试使用深度学习解决生活问题，直接拟合房价。

3.1.2.1 随机森林

随机森林使用了15折的方式训练，在15折的结果中，最优结果的RMSE达到了0.115，在全量预测结果后，RMSE为0.12。具体15折效果如图2所示。

与此同时，使用随机森林的结果来对特征做重要性评估，与直觉相似，房屋面积算是比较重要的特征。

图2 随机森林15折训练效果与样本重要性示例

最终使用随机森林对测试集做预测，得到的结果RMSE为0.12，属于较好的结果。

3.1.2.2 FNN

全连接使用的训练轮数采用了300轮，最终RMSE达到了0.09，其中训练过程如图3所示。在经过100轮左右后，模型逐渐学习到了数据信息，然后继续经过50轮的RMSE快速减少，最终在200轮左右几乎达到平衡，此时模型已经能够拟合到数据，继续训练下去可能会带来过拟合，所以最终我们采用了300轮作为最终训练轮数。

表1 数据展示

图3 全连接训练过程

全连接在最终的预测中，RMSE达到了0.09。

■3.2 实验结果

本文一共采用了两种方案来做房屋价格预测，分别是随机森林回归模型，深度学习全连接回归。最终结果显示，使用RMSE作为衡量指标时，深度学习全连接方案优于随机森林结果，说明全连接预测是一个很好的方案。

4 研究结论与建议

通过本次房屋预测模型的建立，能够得到影响房屋总价值的不仅仅是房屋居住总面积这一个重量级特征，还有街道名称，装修完整度等其他影响特征，并且有些看起来不是很重要的特征也能够影响房价，例如房屋类型功能等。数据帮助我们筛选出重要的特征，排除了一些“想当然”的结果，能够更好的抓住事情的本质，这就是大数据辅助我们解决生活中的事情的实际例子。