一种求解带有昂贵约束的黑箱优化问题的算法研究

冯丹

（重庆师范大学数学科学学院 重庆市 401331）

在实践中，工程设计中的许多约束条件也是在计算上代价昂贵的模型。这种具有昂贵约束条件下的黑箱问题可以被描述为：

由于这类问题的梯度信息不可用，不能使用传统的基于梯度的优化方法求解问题(P)。由于对函数估值次数的限制，不依赖于梯度信息的直接搜索方法和元启发式方法。响应面方法[1]通过已有的采样点及其对应的函数值建立响应面模型(也称为元模型)来近似原有的目标函数，并通过优化响应面或基于响应面的辅助函数得到下一个新的采样点以更新采样点集合，从而更新响应面模型，并找到下一个采样点；重复上述过程，直到满足终止准则。通常采用达到给定的目标函数值估值次数作为响应面方法的终止准则。各种响应面方法之间的区别主要在于响应面模型的选择和新的采样点的选取方式。响应面方法通常采用克里金(Kriging)模型[2]，径向基函数(Radial basis function，RBF)插值模型[3][4][5]，多变量回归样条[6]等。

2018年，Wu 等人[7]提出了一种基于元模型的约束优化方法，称为基于径向基函数的约束全局优化(RCGO)，用于求解涉及计算昂贵的目标函数和不等式约束的优化问题。RCGO 算法首先通过一种序贯抽样方法以获得建立径向基函数(RBF)逼近所有计算昂贵函数的初始点，找到一个可行的解。然后，构造一个受近似约束的辅助目标函数，确定下一个迭代点，并进一步改进可行点。

1 预备知识

由于模型构造的简易性以及在全局逼近上的可靠性，径向基函数插值模型将被用来作为算法中的响应面模型。设是n个两两不同的点，每个点对应的函数值已知。我们寻求如下形式的带多项式尾的径向基插值函数：

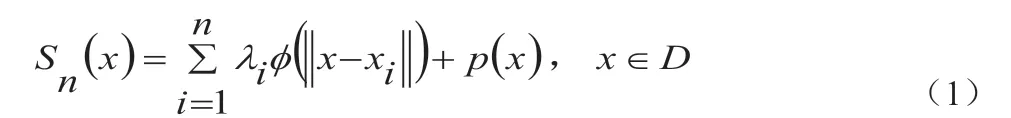
这里||·||表示Rd上的欧几里得范数，为表1 中给出的径向基函数形式中的一种，表示由次数小于等于m 的多项式组成的线性空间。

表1 给出了常用的5 种径向基函数。

2 算法框架

接下来提出了一个基于响应面模型的求解带有昂贵约束的黑箱问题的方法。受RCGO 算法[7]的启发，在RCGO 算法的基础上，加上了自适应采样策略及响应面模型组合策略来求解此类问题。

表1：径向基函数的常见形式（表示相应多项式p(x)的最低次数）

表1：径向基函数的常见形式（表示相应多项式p(x)的最低次数）

RBF 函数 三次函数(Cubic) r3 1 bTx+a 薄板样条(Thin plate spline) r2 logr 1 bTx+a 线性函数(Linear) r 0 a 二次函数(Multiquadric)0 a高斯函数(Gaussian)-1 {0}

表2：测试问题的基本信息

在第一阶段，与RCGO 算法保持一致。通过求解以下子问题来寻找可行点：

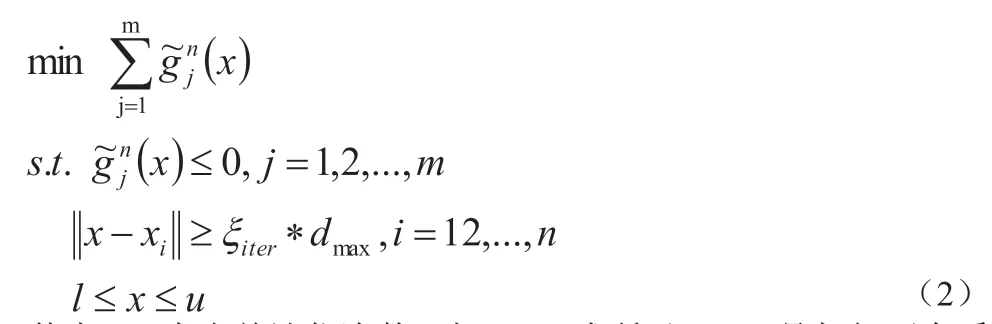
其中，n 为当前迭代次数；如（3）式所示，dmax是任何两个采样点之间的最大距离，是从常数数组得到的距离系数，根据（4）式计算迭代次数。

在得到可行点后，算法进入第二阶段，本章在算法的第二阶段，采用三次径向基函数和薄板样条径向基函数的凸组合生成目标函数响应面模型，当n=n0，即第一次迭代时，组合方式如下：

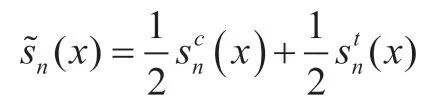
接下来在AMGO 算法[8]构造的辅助优化问题（6）及依次循环选取指数参数以平衡局部搜索与全局搜索的策略基础上，在算法完成了初始迭代之后，增加了根据前后两次响应面全局极小点之间的距离选择搜索类型的准则。如果此距离小于事先给定的阈值，则采用当前响应面的全局极小点作为新采样点，并在下一次迭代中选取适当的指数参数，从而达到自适应采样的目的。

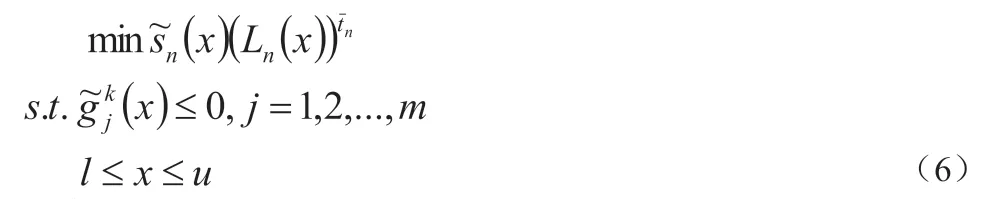
距离指示函数Ln(x)的定义如下：

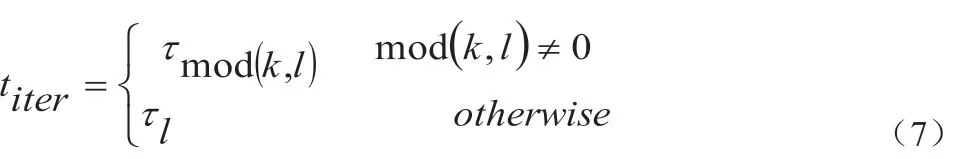
算法1输入：（1）初识采样点的个数n0；（2）最大估值次数Nmax；（3）两种核函数的类型；（4） ；（5）第一阶段的距离系数数组 其中(0 ≤ξ1 ≤ξ2 ≤ξp ≤1)；（6）第二阶段距离指数数组 ，其中(0≤t1≤t2≤tp≤1)；输出：算法搜索到的最佳可行点。步1（初始化）.使用拉丁超立方体采样生成n0 个初始采样点，计算每个点的目标函数值和所有约束函数的值，得到初始样本数据集 ；步2.从初始数据集初始化最佳点xbest，并令n=n0, flag=0；步3. 如果初始数据集中没有可行点，则转到步4；否则转到步5；（第一阶段）步4.执行以下子步骤，直到找到可行点或满足终止条件（即n＜Nmax）；步4.1（拟合或更新响应面模型）使用数据集构建约束函数的响应面模型，其中约束函数的近似模型为 ；

步4.2.计算当前采样点之间的最大距离dmax，并根据迭代次数从 获得；步4.3. 解优化问题（2），选择解作为xn+1；步4.4. 计算xn+1 处的函数值，并将该点加入点集S，令n=n+1；若点xn+1 比点xbest 好，则令xbest=xn+1；步4.5.如果xbest 不是一个可行点，转步4.1；否则，转步5。（第二阶段）步5. 继续执行以下子步骤，直到满足终止条件（即n＜Nmax）；步5.1.利用已有采样点数据构造元模型sc n(x)、st n(x)；并计算模型参数wc n、wt n；步5.1.根据（5）式构造元模型 以及约束函数的近似模型；当images/BZ_148_1692_882_1709_898.png时，使用全局优化算法找到响应面模型的全局极小点 ；步5.2 如果images/BZ_148_1623_982_1640_998.png计算，否则令k=k+1，转步5.2c；步5.2a 如果且flag=0，令采样点xn+1= z*n，flag=1，转步3.3；否则，步5.b 如果flag=1，令k=l-1；如果flag=0，令k=k+1；步5.2c. 根据迭代次数由 得到参数t，用全局优化方法求解问题（6），得到的解作为下一个迭代点xn+1；步5.3.计算f(xn+1)以及g1(xn+1),g2(xn+1),...,gm(xn+1)；步5.4.更新数据集S；步6.返回最优点xbest 以及最优值f(xbest).

在第一阶段，提出的与RCGO 算法保持一致。首先在使用拉丁超立方体采样生成n0个初始采样点，计算每个点的目标函数值和所有约束函数的值，得到初始样本数据集从初始数据集初始化最佳点xbest。如果初始数据集中没有可行点，则转到步4 进入第一阶段寻找可行点，通过数据集构建约束函数的响应面模型，这里采用三次径向基函数来构建约束函数的近似模型为计算当前采样点之间的最大距离dmax，并根据迭代次数从 获得；解优化问题（2），选择解作为xn+1；计算xn+1处的函数值，若点xn+1比点xbest好，则令xbest=xn+1；如果xbest不是一个可行点，转重复步4.1 到步4.5。算法得到可行点后，进入第二阶段，本章在算法的第二阶段，采用三次径向基函数和薄板样条径向基函数的凸组合生成目标函数响应面模型，组合方式如（5）式所示；约束函数的响应面模型依然采用三次响应面模型。并且本章在AMGO 算法构造的辅助优化问题及依次循环选取指数参数以平衡局部搜索与全局搜索的策略基础上，在算法完成了初始迭代之后，增加了根据前后两次响应面全局极小点之间的距离选择搜索类型的准则。如果此距离小于事先给定的阈值，则采用当前响应面的全局极小点作为新采样点，并在下一次迭代中选取适当的指数参数，从而达到自适应采样的目的。算法中参数选取如下：

3 数值实验

为了验证该方法的性能，在一些著名的基准函数上进行了一系列的实验和比较。在测试过程中，测试问题的所有目标函数和约束函数都被视为代价高昂的函数。使用Windows 环境下MatlabR2018a 对算法进行编程实现代价较高的目标函数和约束函数分别用元模型逼近。如表2 所示。

本节主要将新算法的计算结果与COBRA 算法[9]和RCGO算法[7]的计算结果进行比较。我们总共找了10 个测试函数，维数从2 到13 维，包括了7 个Michalwicz 和Schoenauer 测试函数(G1,G2,G4,G6,G7,G8,G9)以及工程设计问题PVD4、SR 和Hesse 测试问题。

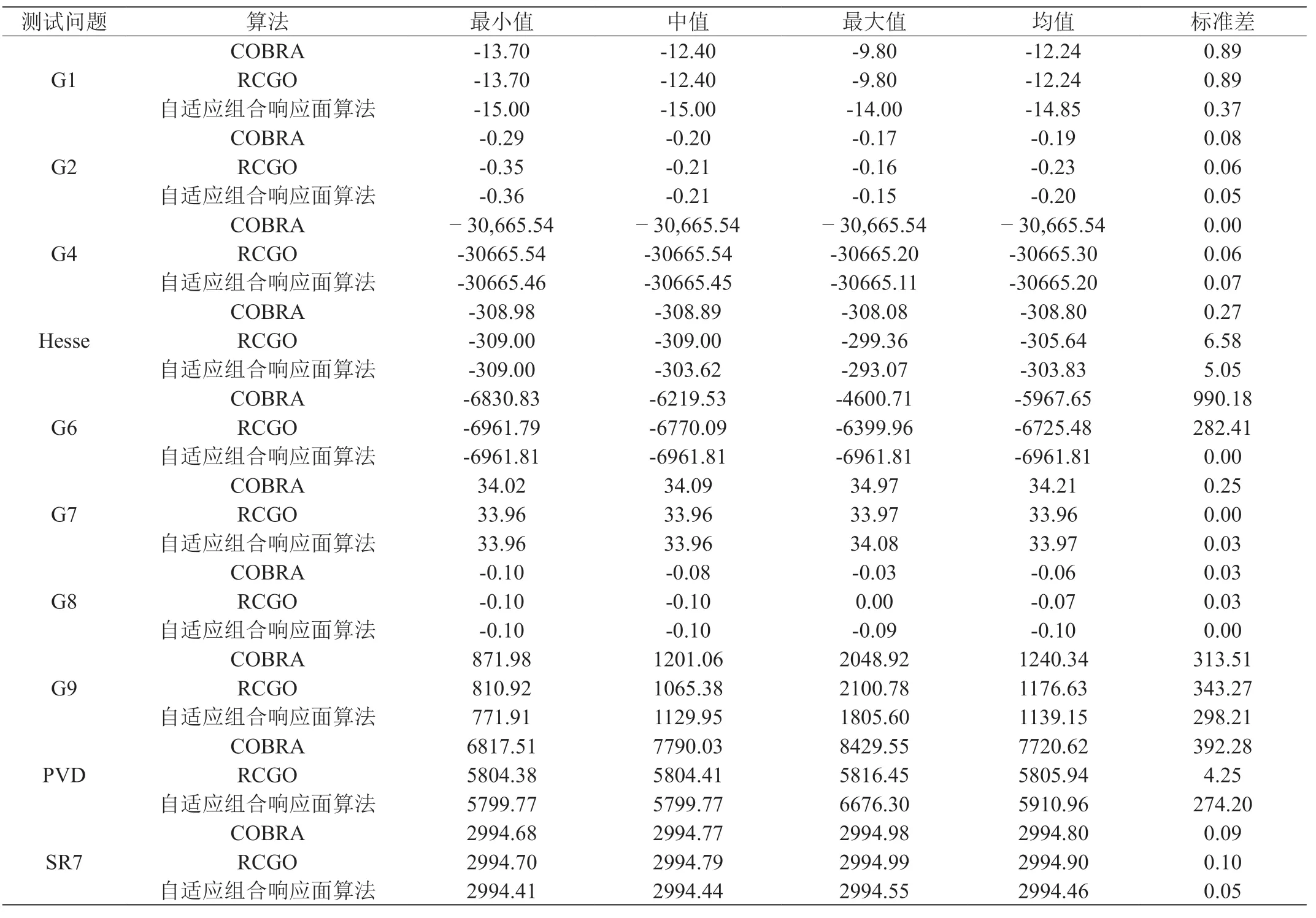
表3：算法在测试问题上的表现

因为算法具有随机性因素，为了更公平地进行比较，每种算法求解每个问题的实验的运行次数都为20,每次运行所允许的最大目标函数估值次数为200 次。从表3 可以看出，自适应组合响应面算法在以下测试问题上的数值实验结果大多数要优与COBRA 算法以及RCGO 算法。

4 结语

在求解带有昂贵约束的黑箱优化问题时，由于约束函数的具体表达式也是未知的，所以可以用响应面模型来进行拟合；同时，为了提高响应面模型的拟合精度，将响应面模型组合策略能应用到拟合目标函数的部分，并在迭代过程中自适应的选取新的采样点，较好的平衡了全局搜索和局部搜索。从数值实验来，在求解带昂贵约束的黑箱优化问题时，取得了较好的结果。