目标临时位置估计的无线网络残差幂次方加权定位算法

赵梦龙

（贵州职业技术学院 贵州省贵阳市 550023）

目前学术界为了可以对非视距环境中目标定位精度有所提升，现有研究中提出可以抑制定位误差的几种算法，主要包括了以下几类，分别为模型法、检测法、应用SN 信息优化算法定位方法[1]。因为第一种所受实际环境动态化、复杂性影响定位模型精度，检测法利用LOS-SN（视距传输静态节点），提出NLOS-SN 的位置估计，对于LOS-SN 节点数条件要求较高。应用SN 信息优化算法定位方法，可以运用LOS 节点和NLOS 节点优化算法，虽然定位精度较高，但是这种算法的计算复杂度也较高[2-5]。所以本文基于传统权重算法优化改进，提出基于目标临时位置估计的无线网络残差幂次方加权定位算法，证实本文提出方法的定位精度相较传统算法明显提高。

1 目标临时定位残差

见图1，根据测量所得SN1静态节点角的到达角，与两个定位圆相交，SN1至TN的测距为圆的半径，如图1所示相交A点，作为TN 的目标临时估计位置。类似就可以运用SN2测量所获到达角，与两个静态节点之间测距，获得另外TN 目标临时估计位置。除此之外还可以将两个定位圆在C 交点，视为第3 个TN 目标临时估计位置[6]。

2 临时定位残差加权算法

假设在目标临时定位共计N 个静态节点，参照以往文献可以轻易获得基于临时定位残差的加权定位算法，可以完成静态节点的分组处理，之后以测距和测角相关信息为依据，每组2 个静态节点，所获C2N 个静态节点组。针对每一个静态节点组来讲，假若较小的临时定位残差值，那么表示该静态节点组作为LOS，反之即NLOS。通过以临时定位残差值的数值为依据，用于分配每一个目标临时位置的相应权重，从而有效抑制NLOS 误差提升了目标临时位置的定位精度。所获每组TN 临时位置及对应权重值，最终确定TN 目标临时位置，公式如下：

图1：定位几何模型图

图2：算法流程图

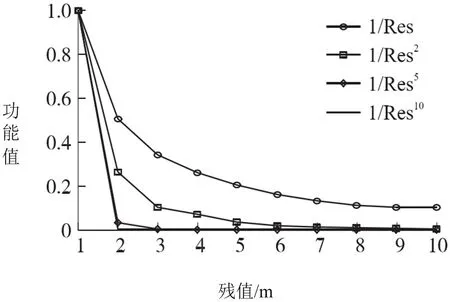
图3：不同加权函数数值变化

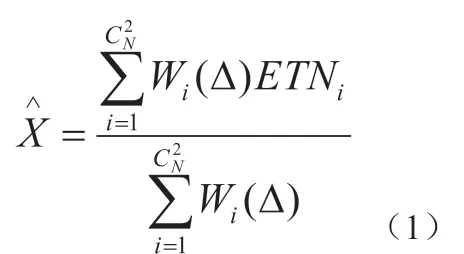
图2 作为本次算法的流程图。

3 仿真分析

3.1 确定加权函数

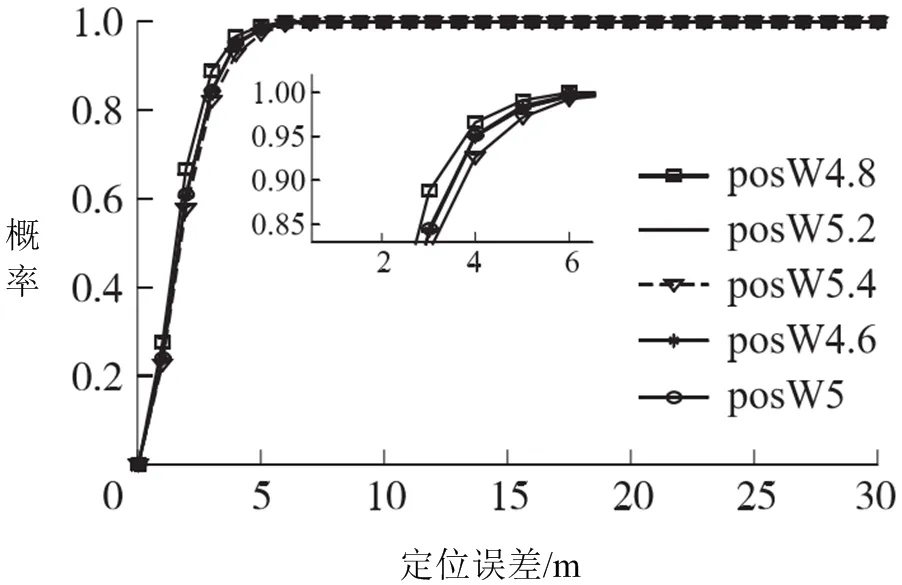
图4：不同幂指数CDF 图

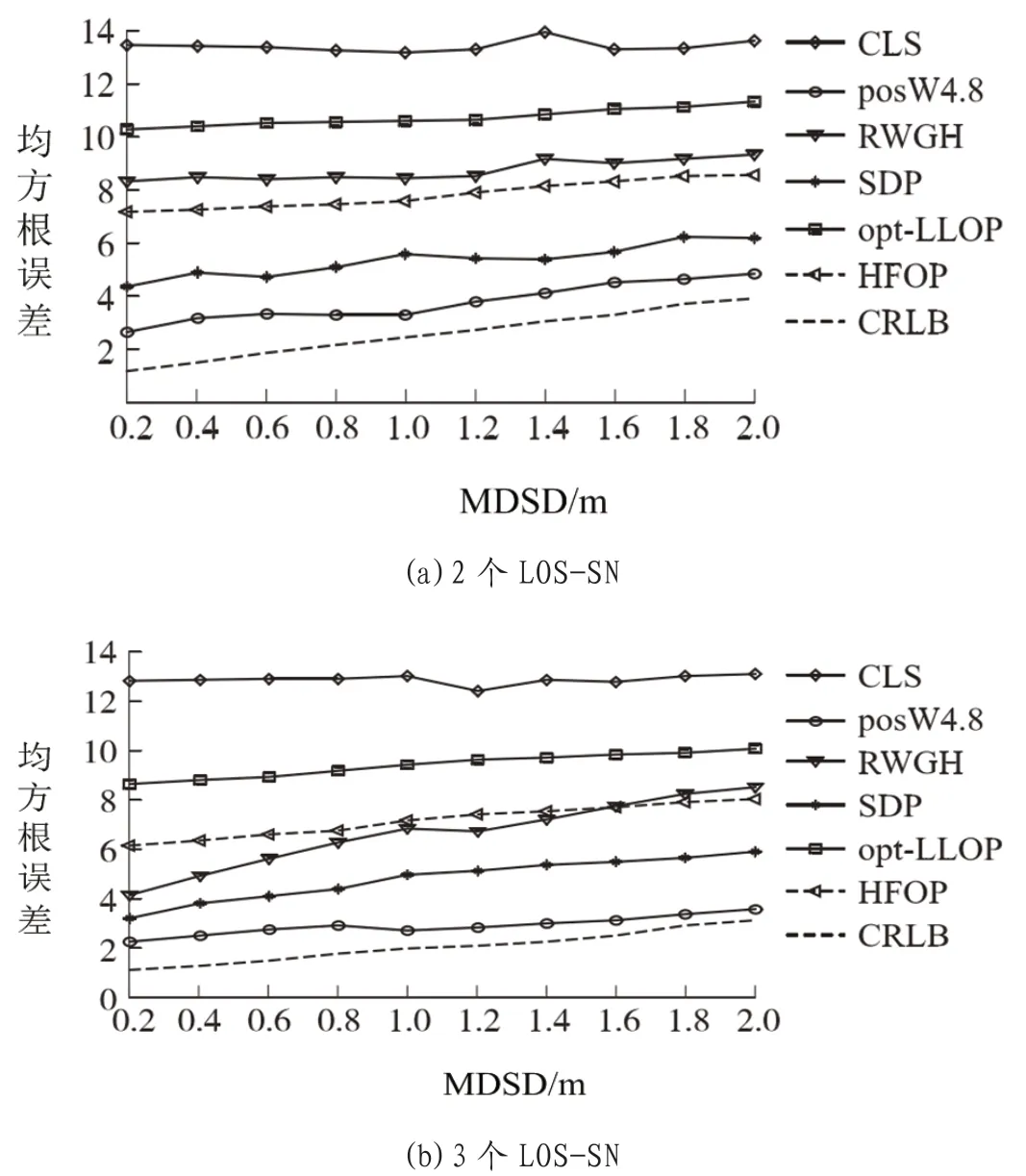
图5：MDSD 对算法精度影响

假设MDSD（测距标准差值）为1m，MASD（测角标准差值）为1°，MLOSmax（最大值）为40m。（见图3）作为不同权重函数数值改变，对比1、2、5 次方加权函数曲线，能够发现明显提升了残差幂次方相应数值定位精度，所以本次仿真选定5 次方加权作为标准进行幂次方小数搜索。（见图4）作为不同幂指数CDF 图，发现在约为5 情况下不存在显著差异，根据仿真结果最终选定了4.8为最优值。

3.2 不同算法相较

在MDSD、MASD、NLOS 三个误差对不同算法定位精准度造成影响的研究中，设定2 个LOS 静态节点和3 个LOS 静态节点运行环境，NLOS 误差均匀分布于0 至最大值之间。分别对残差权重算法（RWGH）、约束最小二称算法（CLS）、凸半定规划算法（SDP）、线性最优化算法（opt-LIOP）、海伦公式最优化算法（HFOP）、本文提出算法（posW4.8）、克拉美罗下界（CRLB）。

3.2.1 MDSD 误差影响

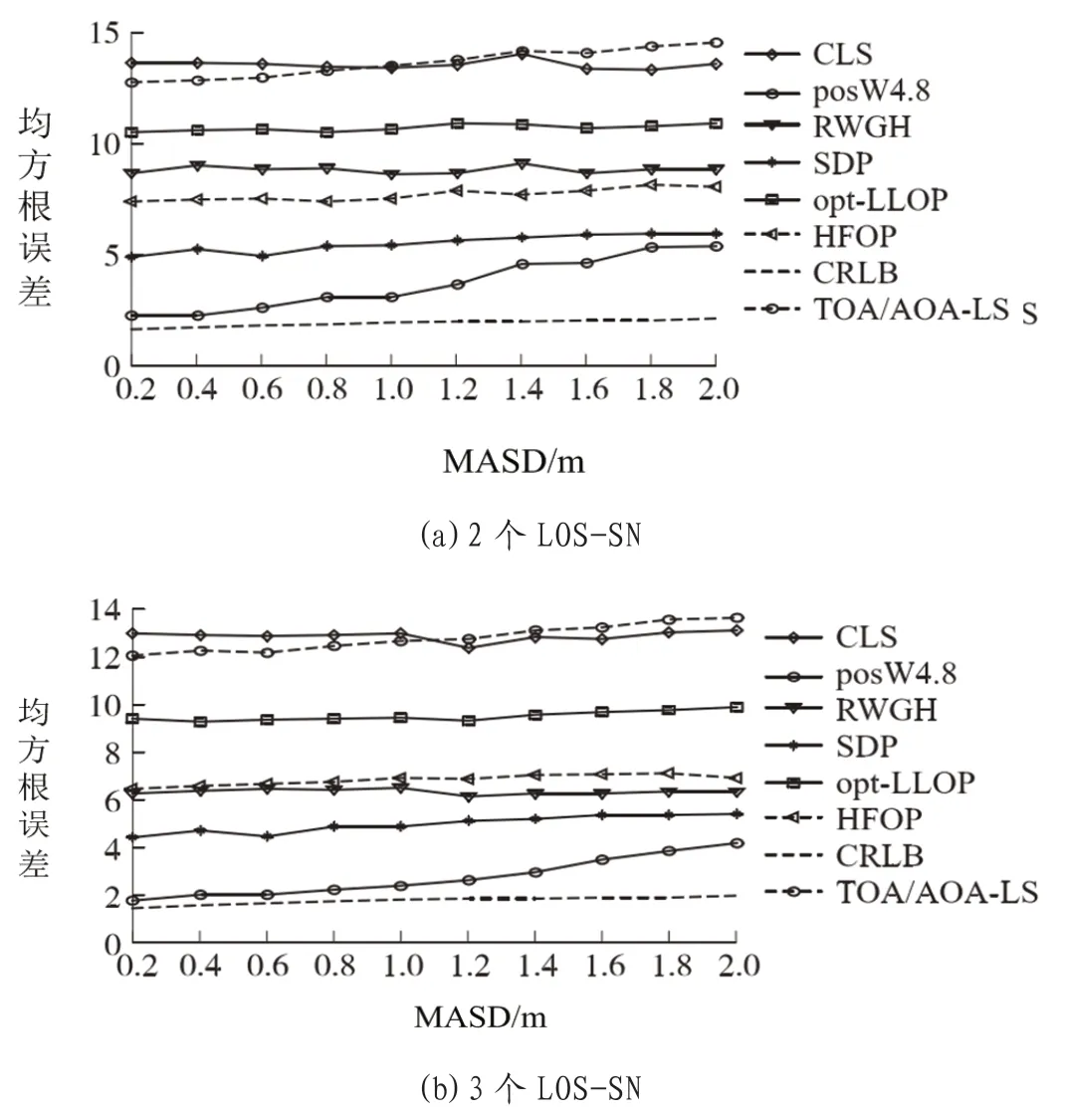
图6：MASD 对算法精度影响

图7：NLOS 误差最大值max 对各算法定位精度影响

在MDSD 误差影响仿真结果（见图5）发现，CLS、opt-LIOP、RWG 和HFOP 运用以上4 种算法会产生较大的目标临时位置估计误差，相比之下，SDP 定位性能较以上四类算法明显改进，尤其对于仅有2 个LOS-SN 条件下，但是相比之下仍然与本文提出算法有一定差距。虽然随着逐渐增加的MDSD 仿真条件，此种算法定位误差逐渐上升，但是相较其他算法略低。出现此种情况原因在于逐渐增加MDSD 在LOS-SN 所获目标临时估计位置相应权重值相应降低，所以降低了定位性能。根据这一仿真结果可以发现，随着逐渐增加LOS-SN 数量，本文提出算法posW4.8 与CRLB 算法的曲线接近，所以证实了本文提出算法LOS-SN 数量随之增加获得更好的目标定位性能。

3.2.2 MASD 误差影响

在MASD 误差影响仿真结果（见图6）发现，随着逐渐增加的MASD 值，在TOA/AOA-LS 除外的算法，其他算法的曲线对比基本持平，这一现象在于算法定位不存在利用角度信息。并且根据对比发现本文提出算法较TOA/AOA-LS 算法，随着逐渐增加的横坐标随之上升，因为逐渐增加的测角误差，降低了分配给精度较高临时位置的预估权值，所以也就相应降低了定位精度。本文提出算法较TOA/AOA-LS 算法的定位精度明显更高，并且本文提出算法还拥有始终保持性能的显著优势。

3.2.3 不同max 值的NLOS 误差影响

在不同max 值的NLOS 误差影响仿真结果（见图7）发现，测距的NLOS 误差最大值表示纵坐标，定位均方根误差表示纵坐标，对比下图各曲线可以发现，RWGH、CLS、opt-LIOP、HFOP 以上四种算法，在逐渐增加的max 值情况下均呈现明显的上升趋势。观察SDP 算法的误差影响曲线，发现在Max 值不断增加情况下，曲线并未达到上文所提这4 种算法的明显上升。但是较本文提出算法明显要高。根据图示曲线情况，可以发现本文提出该算法的定位精度，较NLOS 误差的逐渐增加，仅仅存在略微起伏，整体曲线变动比较平缓，所以表示了尽管在不同max 值的NLOS 误差影响下，本文提出算法依然可以达到较高定位精度。

4 结语

为了对非视距环境中定位精度有效提升，本文提出了基于目标临时位置估计的无线网络残差加权定位算法，在仿真相较其他算法，对于MDSD、MASD、NLOS 三个误差对不同算法定位精准度造成影响仿真条件下，发现在LOS-SN 低于2 时，本文提出无线定位方法的精度较传统非视距定位误差远远较小，提高了60%的定位精度，并且降低了对LOS-SN 的个数要求。