基于PID算法和卡尔曼滤波的平衡车控制系统

杨俊伟

（广东东软学院 广东省佛山市 528225）

1 引言

自平衡车控制系统是移动机器人领域的热点问题，能够将人工智能技术和自动控制理论有机结合的典型应用。随着微电子技术的迅猛发展，自动控制与人工智能的融合会得到进一步提升，平衡车也是未来载具的重要方向之一[1]。本文以STM32 为主控制芯片，在数学模型分析基础之上，采用PID 算法和卡尔曼滤波实现了两轮自平衡车控制系统的设计与实现，由姿态传感器模块收集的倾角、角速度等数据，经过卡尔曼滤波数据融合分析，得到精确的平衡车姿态信息，通过PID 算法实现平衡车的直立控制、速度控制、转向控制、手机蓝牙遥控等，做到了平衡车的速度与稳定性的统一。

2 设计原理

如图1 所示，平衡车的运动状态与倒立的单摆相似，因此，利用可简化的单摆模型进行数学建模,不考虑空气阻力和摩擦力。设车体的质量为m，正常行驶时的加速度为a，平衡车与竖直方向之间的夹角为θ,当平衡车离开竖直方向平衡位置的时候，使重心恢复竖直方向所需拉力为：

当θ 很小时与sinθ 近似，车轮加速度a 与倾角成正比例关系，假设为k，因此可将公式近似为：

上述公式中，加入平衡车角速度ω 的阻尼力影响，可将公式修改如下：

因此，要将平衡车控制在竖直方向的加速度a 的控制公式为：

其中，θ 是倾角，ω 是角速度，k 和k1是比例系数，实际操作时，需要满足k>g，k1>0，实时测量平衡车的倾角，通过卡尔曼滤波和PID 算法给予电机控制信号来控制平衡车的车体维持稳定。

3 平衡算法

3.1 PID算法

PID 算法是平衡车的核心算法，该算法结构简单，参数易于调整，是自动控制系统中经常采用的控制算法。PID：比例单元（P）、积分单元（I）和微分单元（D）组成，PID 算法控制公式如下：

其中：

u(t)为控制器输出的控制量；

e(t)为偏差信号，KP（对应参数 P）为比例系数，TI（对应参数I）为积分时间常数，TD(对应参数 D)为微分时间常数。

直立控制（PD 算法）：比例控制是引入了回复力，微分控制是引入了阻尼力，微分系数与转动惯量有关。Kp 的值越大，系统的反应越快，但是平衡曲线的震荡就较大，我们需要引入Kd 参数来减缓震荡。在小车质量一定的情况下，重心位置增高，因为需要的回复力减小，所以比例系数下降；转动惯量变大，所以微分控制系数增大。在小车重心位置一定的情况下，质量增大，因为需要的回复力增大，比例控制系数增大；转动惯量变大，所以微分控制系数增大。

图1：平衡车的简化数学模型

图2：PID 算法框图

图3：平衡车系统硬件结构图

图4：主控制芯片

图5：姿态传感器MPU6050

图6：蓝牙模块

图7：蓝牙HC-05 原理图

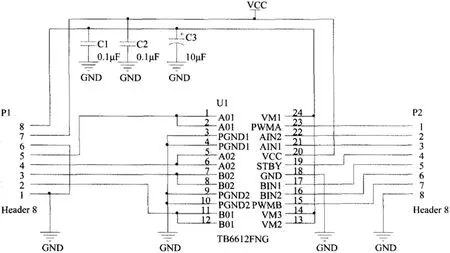
图8：电机驱动器TB6612FNG 原理图

速度控制（PI 算法），积分调节的作用体现为准确性，其作用在于消除系统偏差，KI 越大，系统越准确稳定，但响应时间会变慢。只要偏差存在，就不断地对偏差进行积分（累加），并反应在调节力度上。

在PID 算法中，通过调节PID 这三个参数，就可以逐渐控制系统使其趋于稳定，达到平衡的效果。PID 算法框图如图2 所示。

PID 控制算法因时间离散化不同，通常分为增量式 PID 控制算法和位置式 PID 控制算法[3]。

PID 增量公式：

比例P:e(k)-e(k-1)当前误差-上次误差；

积分I:e(i)当前误差；

微分D:e(k) - 2e(k-1)+e(k-2)当前误差 - 2*上次误差 + 上上次误差

PID 位置公式：

e(k): 用户设定的值（目标值）-控制对象的当前的状态值

比例P:e(k)当前误差

积分I:∑e(i)误差的累加(包括e(k))

微分D:e(k) - e(k-1)当前误差-上次误差

对于E（k）的说明：E（k）这个变量的意义是系统的误差。从公式本身来分析：两个公式都是对系统误差进行的数学运算，增量式公式中与系统前一次的误差E（k-1）和前两次的误差E（k-2）有关。而且位置公式应用时控制的不是输出量，而是输出量的增量，与积分环节无关。适用于步进电机的调节，尤其适用于没有积分环节的控制系统。位置式公式中与系统前一次的误差E（k-1）和误差的累加值ΣE（k）有关，其输出与整个系统的过去状态有关，是对系统每一次不同状态的分析和调整，对系统本身有着较大的影响[4]。

3.2 卡尔曼滤波

由于加速度计静态性能优良但是动态跟踪能力不行，而陀螺仪测量倾角精确但是存在积分误差的累积，因此系统对加速度计和陀螺仪测得的数据通过卡尔曼滤波器实现数据融合[5]。解决了长时间使用陀螺仪而造成的漂移误差，同时也补偿了长时间使用加速度计而造成的动态误差[6]。融合两个传感器的输出数据，根据数据特征建立状态预测方程，对平衡车的姿态角进行估算，得出最优化的车体倾角和角速度，大大确保了数据的准确性，减小了数据的波动。

卡尔曼滤波，也称为线性二次估计，卡尔曼滤波会根据各测量在不同时间下的值，考虑各时间下的联合分布，产生比仅基于单个测量值更精确的未知变量的估计，k 时刻自平衡车系统的预测方程[7]：

A 为系统的预测矩阵，B 为控制矩阵

X(k|k-1):是应用 k-1 时刻的最优解对k 时刻的估计；

X(k-1|k-1):为k-1 时刻的最优解。

经由传感器测量数据修正的状态方程为：

上式中，Kh为卡尔曼增益，其表示方程如下：

X(k|k)和P(k|k)是最新的最优估计，根据卡尔曼的迭代思想 X(k|k) 和 P(k|k) 将会作为新的 X(k-1|k-1) 和 P(k-1|k-1) 进行 k+1 时刻的最优运算。

4 系统硬件设计

系统以Stm32F407VGTx 为主控制芯片，硬件模块主要有：电姿态传感器模块、电机模块、蓝牙通讯模块等。如图3 所示。

4.1 主控制器

如图4 所示，平衡车系统主控芯片采用Stm32F407VGTx，STM32F407 系列MCU 具有高集成度、高性能、嵌入式存储器和外设的医疗、工业与消费类应用。具有512KB~1MB Flash 和192KB SRAM，采用尺寸小至10×10 mm 的100~176 引脚封装。提供了工作频率为168 MHz 的Cortex ™-M4 内核（具有浮点单元）的性能。

4.2 姿态传感器

姿态控制模块采用MPU6050 传感器，是InvenSense 公司推出的一款六轴运动处理芯片，集成了三轴陀螺仪及三轴加速度计传感器，内置两组I2C 接口，分别用于通信和连接外部磁力传感器。MPU6050 采用自带的数位运动处理器DMP（Digital Motion Processor），通过主I2C 接口，以单一数据流的形式直接读取完整的9 轴融合演算数据并向应用端输出。本系统以I/O 口模拟I2C 与MPU6050 通信获取数据，再利用卡尔曼滤波算法解算出当前平衡车的倾角和角速度。如图5 所示。

4.3 蓝牙模块

蓝牙模块如图6 所示。

如图7 所示，HC-05 是一款高性能主从一体蓝牙串口模块，具有成本低、体积小、功耗低、收发灵敏性高等优点。HC-05 具有两种工作模式：命令响应工作模式和自动连接工作模式。当模块处于命令响应工作模式时能才能执行AT 命令，可向模块发送各种 AT指令，为模块设定控制参数或发布控制命令。

4.4 电机模块

电机模块主要是由直流电机、电机驱动器和电机测速器组成，电机选择供电电压为12V、减速比为1:30 的直流减速电机，型号为JGB37-520。电机驱动模块采用东芝半导体公司生产的一款直流电机驱动器件TB6612FNG，具有大电流MOSFET-H 桥结构，双通道电路输出，可同时驱动两个电机，分别用来控制平衡车的左右轮。电机转速检测采用增量式磁性编码器，霍尔编码器是电机测速中常用的电子元件，通过输出两个通道正交相位90°的方波把速度数据传输给单片机。如图8 所示。

5 总结

本文提出基于PID 算法和卡尔曼滤波数据融合的平衡车控制系统设计与实现，本系统以PID 算法为核心，由卡尔曼滤波对加速度计和陀螺仪传感器数据融合实现系统的最优估算。根据实测，系统具有调节速度快、精度较高、抗干扰能力强等优点，具有一定的实际应用参考价值。