模板匹配技术在图像识别中的运用

朱泓谕

（东莞理工学院网络空间安全学院 广东省东莞市 523808）

在模式识别领域，模板匹配属较为常规的方法，确定对象物在图像中的位置，由此完成对象的识别操作。现有经验表明，模板匹配技术在条码识别、指纹识别等应用场景中均具有可行性。

1 模板匹配技术在图像识别中的运用实例

模板匹配技术得以实现的关键前提在于得到数学函数的支撑，准确确定被搜索图的坐标关系，将其代入数学模型内，做相应的处理。模板匹配技术是模式识别领域应用较为广泛、效果较为良好的方法，但在面对各类干扰因素时，需要协同运用数学模型，更好地满足图像识别的质量和效率等层面的要求。

1.1 条码识别

模板匹配技术已经在条码识别领域取得较突出的应用效果，其中变造币横竖条码是基础，确定特定的数轴，在该基础上增添二维图像的灰度投影，再依托于已经建立的数学模型，高效完成在数轴上的匹配操作，期间产生的噪音可相互抵消，可减小干扰，因此有利于提高识别的效率、降低识别错误现象的发生概率。

垂直于水平2 个方向的图像可根据灰度分布特征做特定的灰度投影操作，此方式下将生成模板投影所对应的投影序列，与此同时也能够得到等待匹配图像的投影序列，再将两者加以匹配，确定相关值，将该结果代入投影函数内。模板匹配具有动态化的特性，具体体现在模板投影曲线的层面，其存在上下滑动的变化特点，经过对比分析后，若两幅图具有相匹配的关系，则意味着相关函数最大值较大，即超过门限值。

1.2 指纹识别

依托于模板匹配技术，可以有效缩短指纹识别的持续时间，其中多道计算步骤均可以得到精简处理，由此在较短的时间内完成了匹配操作。整个匹配过程具有阶段化的特征，其匹配操作可以分为多个细分的环节：每间隔M 个点搜索下匹配结果的优劣，从中做出甄别，确定存在极大匹配的周边，针对该范围的参考值的位置做匹配操作，全过程中匹配点得到有效的保留，可以较好地规避匹配点丢失的情况；在前述基础上，对M 个点随机计算，生成突出特征随机序列，其意义在于可决定后续计算误差的先后顺序；经前述流程后，最后抛弃固定阈值，从中选择最具应用价值的单调增长性阈值序列，此时可以规避匹配序列的阈值点丢失的问题，识别结果的精度得到保证。

1.3 字符识别

实际运用中，主要考虑如下两种情况：

（1）采用以特征加权为基础的模板匹配模型。通过特征加权方法的应用，能够对字符笔数做全新的分配处理，根据权重对其顺序做出排列，其中权重较高者集中在中心位置，相比之下权重较低者则普遍分布在边缘处，此时样本模板与标准模板可高效匹配，再借助预设的模糊识别规则，完成相应的识别操作。识别流程中，针对各字符做加权处理，得益于此方式，可有效提高识别率。

（2）采用以特征块为基础的模板匹配模型。针对模板采取切割处理措施，由此得到大小具有一致性的方块，再确定各自所包含的点，完成对标准模板的匹配操作。需注意的是，此处所提的字符在执行匹配操作前便经过了深度的改造处理，因此产生的特征模块数量较少，相比于前述方法而言，其工作量有所精简，在效率方面的优势更为突出。

1.4 基于不变矩的图像匹配

基于不变矩的图像匹配包含多种形式的畸形不变性，是高度浓缩的图像特征。在识别与匹配工作中，围绕图像轮廓和检测模板两部分展开对比分析，向其中增添遗传算法，通过旋转、平移等方法的应用，完成对图像的匹配操作。在该方法之下，所创造的综合应用效果明显优于常规算法。

2 模板匹配序贯相似性检测算法（SSDA）

在数字图像中，依托于如下所提的公式（1）展开计算，确定在点(i,j)时的非相似度m(i,j)，将其视为匹配尺度。

图1

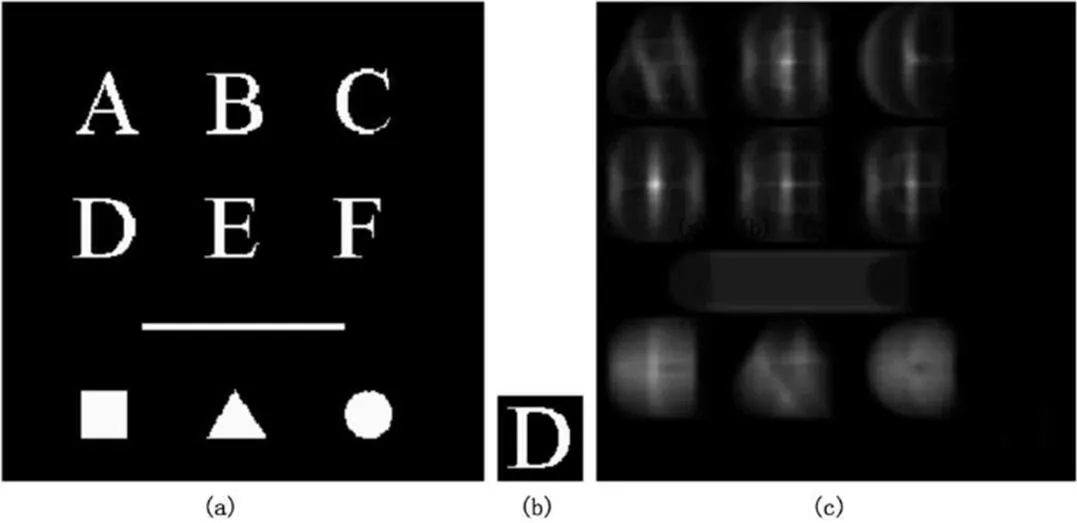
图2：匹配图像

图3：模板处理

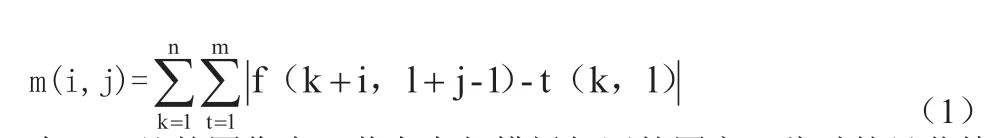
在(i,j)处的图像中，若存在与模板相同的图案，此时的显著特征在于(i,j)值明显较小，若不存在则有该值较大的特点。在作加法时，着重考虑的是灰度差的绝对值的和，将其与特定的阈值展开对比分析，若前者偏大，则说明该位置无与模板相同的图案，为进一步做出判断，将会转至下一位置，继而按照相同的方法计算m(i,j)。按照该流程以富有秩序性的方式推进，可以有效缩短计算时间，以较高的效率完成匹配操作。

沿着前述所提SSDA 算法的运用思路，在原有基础上加以优化，以期提高该方法的可行性。对此，对图像上的模板移动做出划分处理，按顺序操作。首先为粗检索，将模板与图像重叠（每隔若干个像素），经计算后确定该匹配的尺度，此操作的作用在于可确定待寻找图案的初步范围；随后进入细检索环节，进一步精准锁定待寻找图案的位置，操作方法为模板每隔1 个像素移动1 次（相比于粗检索而言，模板移动的频率有所增加），由此便可得到具体的位置。

可以发现，在该改进后的SSDA 方法中，模板匹配的次数明显减少，但也存在局限之处，即有可能漏掉图像中最合适的位置。针对此问题，以VisualC++610 为平台，组织开发工作，生成一套数字图像处理程序，在其支持下，能够完成模板匹配运算操作，在提高识别效率的同时避免图像遗漏的情况。

其中，图1 中(a)为原图,(b)为待匹配的模板,(c)为匹配后模板在原图中的位置（可以高效地与原图展开对比分析）。

3 其它的模板匹配快速算法

匹配算法的总计算量取决于两方面因素，具体可利用如下关系式加以表示：总计算量=（选择算法的计算量）×（搜索位置数）。根据此特点，可以探寻除了前述所提内容之外的一些其他具有可行性的方法，具体做如下分析。

3.1 相关算法

关于两个函数的相关性，可用式（2）予以表示：

式中：f*为f 的复共轭；F(u,v)和H(u,v)分别为f(x,y)和h(x,y)的傅立叶变换。

依托于卷积理论，可以对前述公式做进一步的延伸，具体如下：

卷积的重要性在于其在空间域过滤和频率域过滤间扮演着“中间联系者”的角色，是实现匹配的基本前提。具体而言，在匹配工作中，f(x,y)指的是某特定的图像，若要对f 进行分析以便判断其是否含有感兴趣的物体，则需要引入h(x,y)，将其视为该物体（此处将该图像称为模板），若能够成功匹配，两函数的相关值会在h找到f 中相应点的位置上达到最大。

结合前述分析，相关算法含两种细分的方法，即在空间域或频率域均可以进行。其中，图2(a)呈现的是大小为M×N 的图像；图2(b)呈现的是寻找与J×K 相匹配的子图，即w(x,y)。具体相关关系可利用如下公式表达：

在两种方法的选择中，可以在频域中实现相关算法。

选取基准图和实时图，将两者做二维离散傅立叶变换。

关于基准图的变换结果，如下：

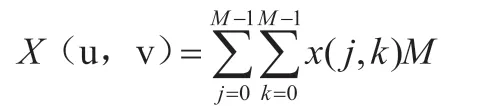
式中，u 和v 分别对应的是j 和k 方向的频率变量。

关于实时图的变换结果，如下：

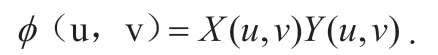
3.2 幅度排序相关算法

分阶段完成算法的相应操作：首先，从实时图中提取灰度值，以幅度为依据加以排序，再于该基础上完成二进制编码操作，此时可以实现对实时图的变换处理，即形成集合{Cn,n=1,2,…,N}；随后，在确定前述各类二进制序列后，将其与基准图进行相关，全程遵循“由粗到细”的基本原则，在循序渐进的工作方式下，可从中确定合适的匹配点。

3.3 主要问题分析及对应的解决办法

前述所提的模板匹配方法均建立在理论环境中，在理论层面具有高度的可行性，而就实际应用情况来看，其潜在诸多干扰因素，例如多类噪声均会对图像（模板）造成干扰。但在该过程中若模板受到外部因素的干扰，正常工作机制将难以有效运行，会严重影响正常识别进程，因此需针对该部分采取预处理措施，最大限度消除干扰。在此条件下，假定图像中有噪声，则其矢量表现形式为：

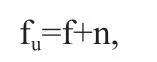
式中，f 为确定性图像，n 为噪声，fu为实时图像。在具体分析中，需要着重考虑噪声n 的产生机制以及具体的成因，再消除该部分噪声。从实际环境来看，n 的情况较多，为精准分析以及消噪，则必须明确具体的成因，据此设计滤波器m，利用该装置完成对实时图像的过滤处理，进而达到消除噪声干扰的效果。假定f0=mfu,在该关系式中，最佳状态是f0 尽可能接近f，在此条件下展开匹配运算。而为了完成前述所提的一系列操作，则需要针对图像采取增强、平滑及复原处理措施。

关于受污染的模板，如图3(a)所示。结合图中内容展开分析，在噪声的污染作用下，模板的匹配精度受到影响，其难以精准匹配至原图相应的位置处。针对受污染模板采取还原与增强操作后，得到全新的图像，具体如图3(b)所示，可以发现，此时模板的总体状况得到显著的改善，可以精准地匹配至原图对应的位置。图3 中，在探明噪声干扰的具体作用机制后，可采用滤波的方法加以处理，使模板复原。然而，此类滤波器m 的设计难度较大，因此也是阻碍模板匹配发展的关键因素。在该背景下，应当探寻适用于模式识别的更为可行的发展路径，纵观现有技术水平以及实际发展成果可以得知，以自适应控制、模糊逻辑、神经网络较为典型，其均是综合应用效果较为良好的数学模型建立方法，在模板匹配技术的数学模型建立工作中可灵活应用特定的方法。

4 结语

综上所述，通常而言，模板匹配的识别能力较强，但该特性并不具有绝对性，即在部分干扰较严重的环境中将出现模板匹配识别不适用的情况，或是在模板改动时也存在此类情况。因此，需深入剖析，选择更为可行的数学工具，例如通过自适应控制、模糊逻辑、神经网络等方法的应用，建立科学的数学模型，诸如此类技术均是模式识别领域的重要发展方向。在后续的发展中，应当围绕模板匹配做更为深入的研究，夯实理论基础，提高对先进方法的应用水平，进而建立更为可行性的数学模型。