椭圆形量子围栏的表面电子态

杨爱云

（西安交通工程学院 陕西省西安市 710300）

1 引言

世界上第一台扫描隧道显微镜（Scanning Tunneling Mciroscope简称STM）是Binning 和Rohrer 成功研制的。借助STM 人们可以直观地观察到物体表面的原子结构，使人们从对微观原子的想象中跳出来，它比同类原子力显微镜具有更加高的分辨率。并且因STM 观测不需要制样，所以观察和测量过程中不会对样品表面造成任何损伤，被广泛地用于测定材料的物理、化学和生物性质，并成为纳米加工的关键技术，同时STM 还可以通过其针尖与表面原子的相互作用，操纵单个原子和分子的排列[1-2]，成为近年来发展起来的一种扫描探针显微技术。

IBM 研究中心的研究小组利用扫描隧道显微镜(STM)将用电子束蒸发到Cu(111)表面上的48 个Fe 排列成一个圆圈，这个圆圈的平均半径为7.13nm，相邻铁原子之间的平均半径为0.95nm，虽然这个圆圈是由分离的铁原子组成的并不连续，但却能够像栅栏一样，围住Cu 表面的电子，因而人们形象地将这个铁原子圈称为量子围栏[3-4]，如图1 所示。

科学家还用STM 在Cu(111)表面上将Fe 原子围成了其它形状的量子围栏[5]，如矩形（图2）、椭圆形（如图3）、三角形（如图4）、六边形（如图5）等。通过对圆形量子围栏电子态的理论分析表明其概率密度仅与径向函数有关，而与横向函数无关，概率的二维分布为各向同性，等概率线是以坐标原点为中心的同心圆，这与图1中所反映的实验结果一致[6]。

研究者在Cu(111)表面上用STM 将36 个钴原子摆成椭圆形，将一个磁性钴原子放置于该椭圆形量子围栏的一个焦点上，将会在椭圆形量子围栏的另一焦点上检测到具有自旋同向的电子讯号，而该焦点实际上并没有放置任何原子，但将此磁性钴原子放置于其他地方，则完全检测不到任何电子讯号。这表示原子上电子密度经由周围表面电子波，传讯讯息至另一个焦点[7]。该发现可作设计未来纳米IC 元件中的传导线。

但目前国内外大多数人都是借助于数学软件(Matlab，Mathematica 等)计算机模拟量子围栏的电子态，并且与实验结果对比说明低维物理体系的电子态分布[7]。通过理论分析量子围栏的电子态的研究，仅现于简单的矩形、圆形等。椭圆形量子围栏的理论分析还没有发现。

本文通过理论分析椭圆形量子围栏的电子态，为进一步研究量子围栏提供一定的数据参考和理论基础，对借助于计算机模拟电子的分布图有一定的指导作用。其研究结果有一定的科研价值，也有助于人们对微观世界的认识。

2 椭圆形量子围栏的建模与分析

用Fe 原子在Cu 的表面排列成一个椭圆形即一个椭圆形量子围栏，Cu 表面的电子被束缚在这个椭圆形围栏内，由于Fe 原子对Cu 表面电子的强烈散射作用，在这个椭圆形围栏内就会形成同心椭圆形驻波，此时，可以把这个椭圆形量子围栏看作是一个二维无限深势阱，也就是一个二维无限深椭圆形势阱。在这个模型中，被束缚在椭圆形势阱中Cu 表面的电子，满足二维定态薛定谔方程[8]：

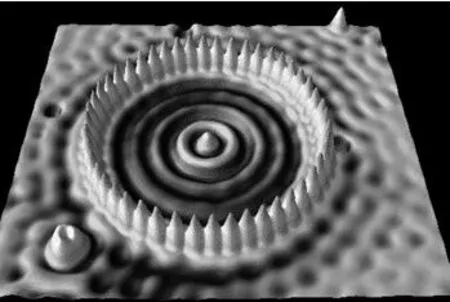
图1：圆形量子围栏

图2：矩形量子围栏

图3：椭圆形量子围栏

图4：三角形量子围栏

图5：六边形量子围栏

设Cu 表面电子的能量为E， Cu 表面电子的质量为m，椭圆形量子围栏的半径为M，在二维椭圆柱坐标下，被束缚在椭圆形势阱中的电子所具有的势能为：

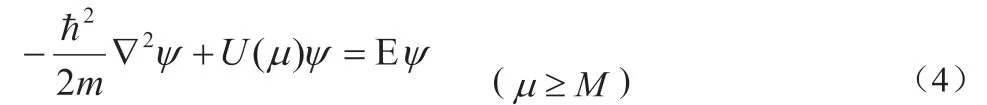
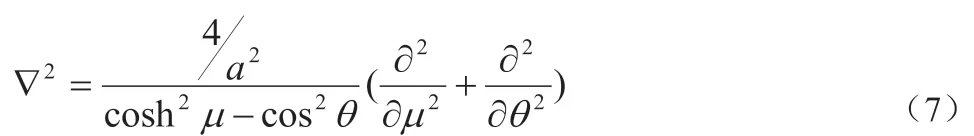
将（7）式代入（6）式得：

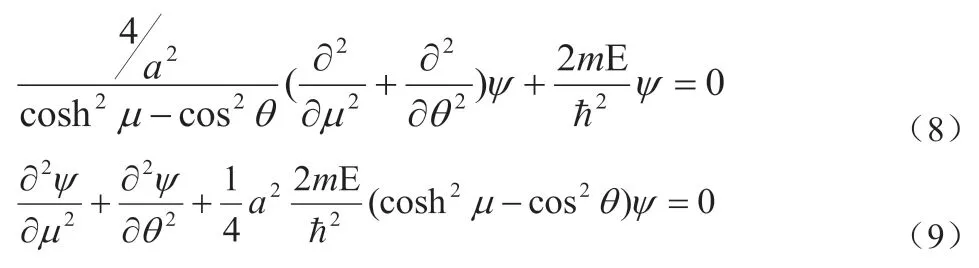
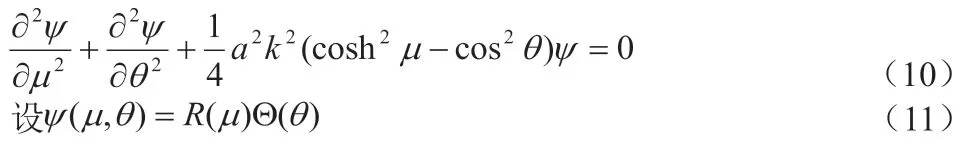
将（11）、（12）、（13）代入（10）式，并用R(μ)Θ(θ)除以方程的两边得：

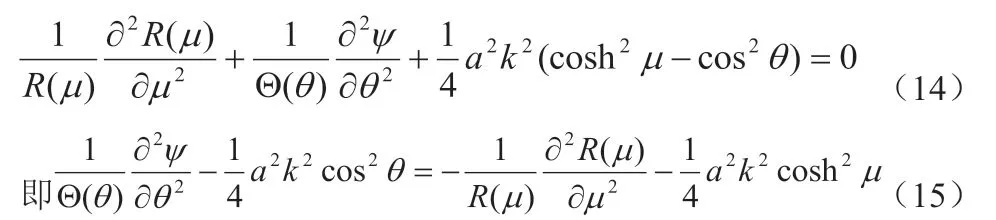
这个方程的左边仅是与θ 有关，右边仅是与μ 有关，且θ 与μ都是独立变量，因此，只有等式的两边等于同一个常数时（15）式才成立。用-b 表示这个常数，同时令

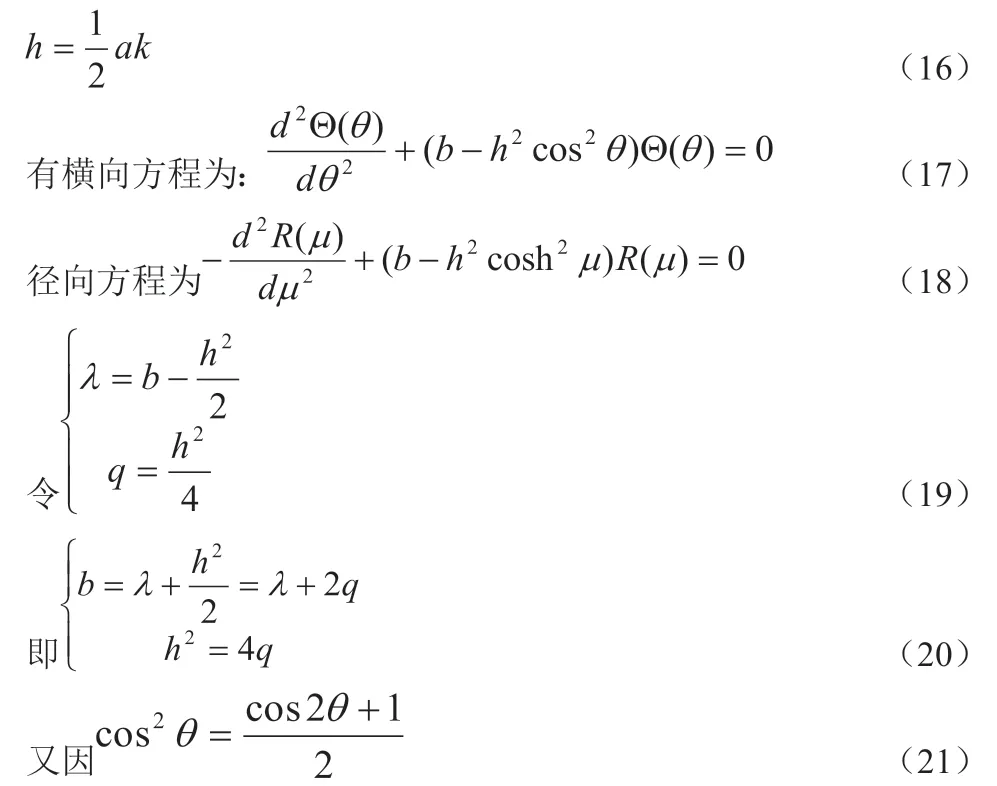
将（19）、（20）代入式（17）式得：

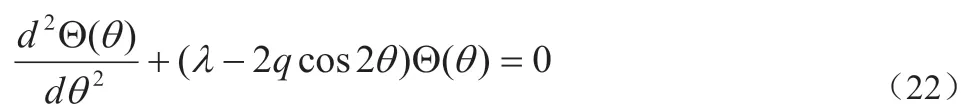
（22）式为马丢方程[9]，其解为马丢函数[9]。

（22）式的通解[10]为：

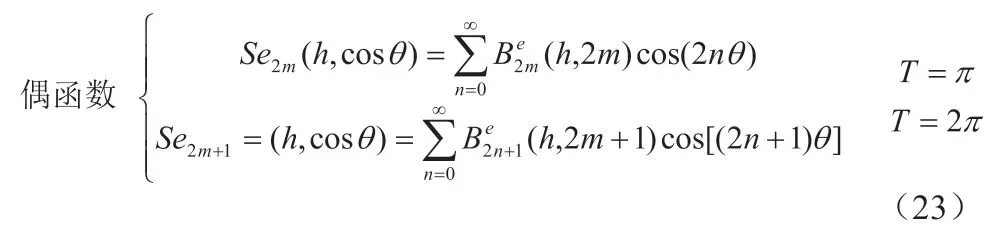
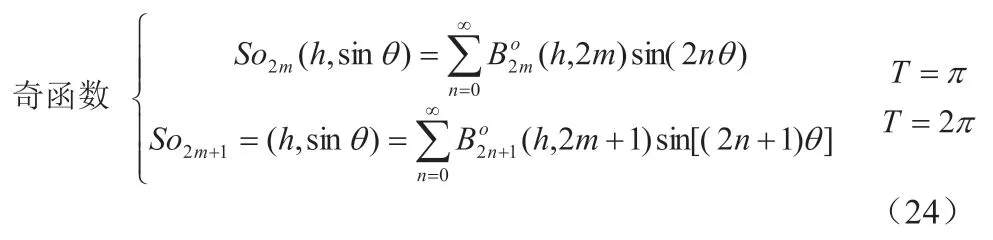
其中T 表示周期。

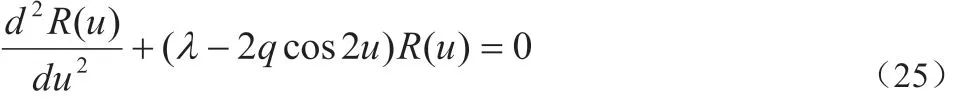
也将（18）式化为马丢方程[9]。

则（18）式的通解[10]为：

综上所述，该椭圆形量子围栏电子的波函数表达式为：径向解与横向解的组合，即偶函数和奇函数

3 结论

将椭圆形量子围栏作为二维无限深势阱来处理，找到了能恰当描述电子势能的势能函数，并得出了通解。但是在求解过程中得到的是马丢方程，其解为马丢函数，由于其求解过程以及求解其本征值比较复杂，我还将继续研究，其结果将会在后续研究中给出。