源于“结构化” 教学有延展

顾军宏

摘 要：《四边形的认识》一课属于空间与图形中的图形认识与论证领域，在教学中应帮助学生建立初步的知识结构体系，在“结构化”教学中需要进一步思考需要筛选或吸纳的内容，在教学的延展中让基本知识和基本方法得以建构。

关键词：小学数学;结构化;教学延展;四边形的认识

《四边形的认识》是“图形与几何”领域中一个极其经典的教学内容，如此定位，与它自身在整个小学阶段的“形概念”教学中特有的地位分不开。首先，它是学生对平面图形的认识从外部特征到内部要素转变的起始课;其二，《四边形的认识》一课除了要让学生认识四边形的特征，还要让学生学会从“边”和角的角度来判断认识图形，它是认识其他平面图形认识学习方法的奠基课。笔者对本课进行实践探究及研讨过程中，通过借鉴、学习、吸纳，对源于“结构化”的教学如何合理延展方面有所感悟。

一、思考与求证：四边形的认识“结构化”教学的价值

（一）教材的“前世”到“今生”——删繁就简凸显概念本色

《四边形的认识》是人教版从实验教材到现行教材（2011版）变化较大的内容之一，在实验教材中，安排了比较大的篇幅呈现四边形的学习，引导学生经历“从校园熟悉的场景中寻找四边形—从众多几何图形中找出四边形—对四边形进行分类”一系列的过程。而在2011版教材中却只用了一个页面的内容，对比之下，一种干脆利落、直达主题的意图跃然纸上。教材为何有如此大的改变？笔者以为原因有以下几点。

1. 基石稳妥方能拾级而上

如果要对所有的四边形进行细致分类，必须以全面掌握各类四边形的特征为前提。但是，实验教材中编排的“图形分类”的内容，教材中呈现的图形有长方形、正方形、平行四边形、梯形和菱形等。事实上学生尚未掌握各种四边形的特征，在此基础上让学生对所有的四边形进行细致分类，是不合适的。

2. 抓住核心，避免本末倒置

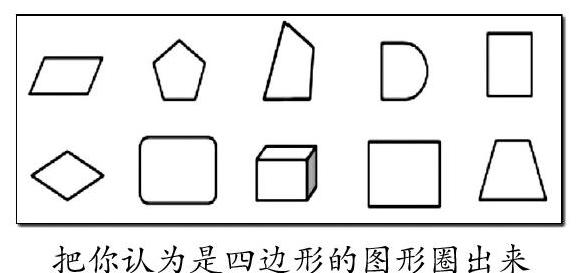
小学阶段“图形的认识”教学内容循序渐进，教学要求逐步提升。《义务教育数学课程标准（2011年版）》第一学段的“图形的认识”的具体目标中指出：“辨认长方形、正方形、三角形、平行四边形、圆等简单图形。”根据“具体目标”的这一要求，显然，第一学段中对梯形和菱形等图形的认识不作要求。由于上述原因，编者有意识地将实验教材中例2的“图形分类”删去，单刀直入地聚焦于“把四边形的图形圈出来”，引导学生将注意点全部放到四边形的特点上。

注意：从教材的变化中，清晰地呈现了以四边形的认识作为“边”“角”研究起点的路径，也就是说，要研究其他特殊的四边形，这一课是整个四边形框架结构的主心骨。

（二）学生的“已知”与“未知”——面体关联结构不清

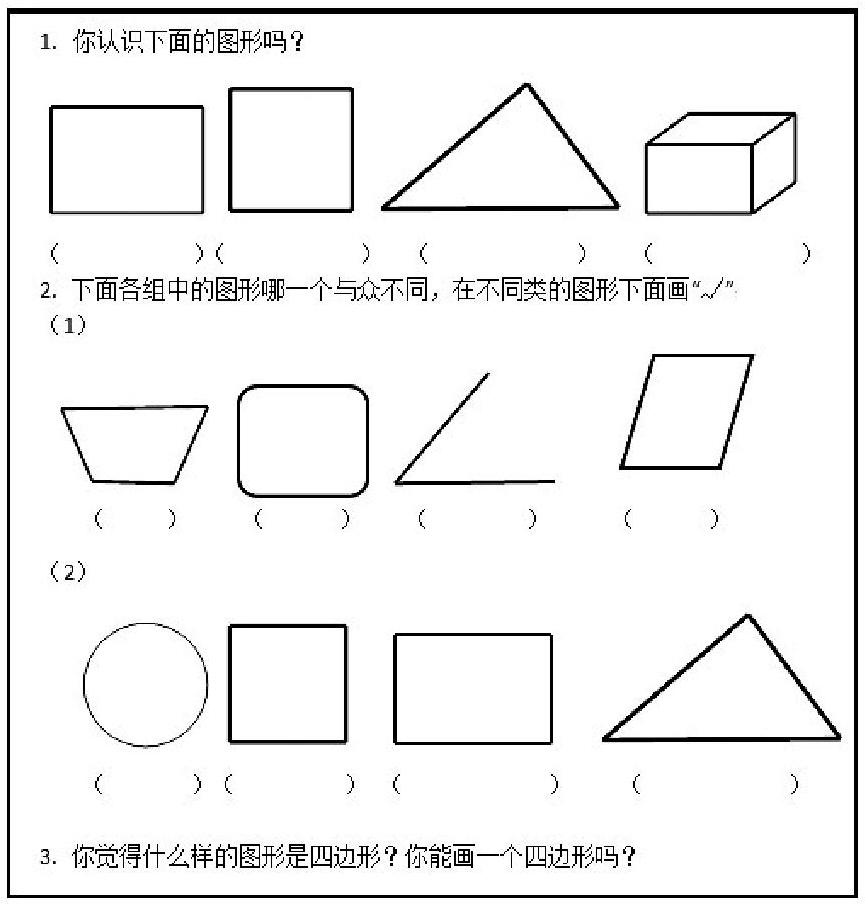
学生在一年级学习了认识立体图形以及认识平面图形之后，对于图形有了一定程度的认识，二年级初步认识了角，这也是学生首次接触“不封闭图形”，那么学生对这些知识的掌握程度如何？在日常生活中，学生一定也接触过很多四边形，那么他们心目中的四边形又是怎么样的呢？为了更好地了解学生对四边形相关知识的了解程度，笔者设计了如上图所示的前测练习。

1. 对平面图形的认识优于立体图形

第一题，学生的答题情况反映出的一个问题是：所有学生都能正确写出前面三个平面图形的名称，而难以分辨第四个立体图形。从结果中不难看出，学生对平面图形的认识要优于立体图形，说明这类四边形以及三角形的命名对于学生来说并不困难。

2. 对边是否全部围成的及曲边划分不够明朗

在找不同的题目中，学生对到底是选第二个图形还是第三个图形产生了疑问，归根到底是学生没有建立起图形的逻辑结构，学生无法区分没有全部围成的图形和有曲边的图形，因此这一点应当在教学中予以适当说明。

3. 对于直边曲边的区分较为清晰

在有曲边的和都是直边的图形中，学生都能迅速判断出第一个图形是“与众不同”的，因为他们能一眼看出边的曲直，说明学生对于边的曲直的区分较为清晰。

4. 对于特征的表述水平远低于对图形的判断水平

大部分学生认为“有4条边的图形”就是四边形，很少有学生能完整表达出“有4条边和4个角的图形”是四边形，给出的名称让学生更倾向于从边的角度关注。在画四边形的时候，学生画的都是较为特殊的四边形，说明在他们的认识中，四边形就是正方形、平行四边形这一类他们熟悉的图形，对于四边形的特征并没有比较深入的理解。

注意：前期的經验让学生更早接触的是特殊的四边形，但这样的认识是零散的，需要帮助他们找到关联整个平面图形的结构，才能触类旁通。

二、借鉴与吸纳——四边形的认识“结构化教学”所需

1. 在别人的课堂中探索

作为一个经典的教学内容，《四边形的认识》被许多优秀教师精彩演绎，笔者曾在磨课过程中聆听了两堂精彩的展示课。带着“结构化”的思考，笔者对两堂课进行借鉴与吸纳。

[李老师的教学]

用4根小棒搭一个四边形：学生先自己独立搭一搭，然后和同桌说一说是怎样搭成一个四边形的。

学生介绍自己是怎样搭的。

根据学生的回答，教师适时提问：对齐是什么意思？

展示学生没有完全连接上的作品，师生讨论，得出必须封起来，这样才是四边形。

小结：要搭成一个四边形，必须把头和尾相接起来，这样的图形给它一个名字，叫作封闭图形。

（学习单）画出你心目中的四边形。

（展示学生作品）师提问：他们画的四边形形状各不相同，为什么都叫四边形呢？根据学生回答得出：用4条线段围起来的封闭图形是四边形（板书：由4条线段围成的封闭图形）指出4条边，4个角以及对边。

[郑老师的教学]

出示前测中的学生作品进行逐层辨析，师生共同研究四边形的特征，得出四边形的特征：有4条边和4个角。

（学习单）学生先独立探究，再交流：

请通过量一量、折一折等方法验证长方形和正方形的边和角的特征。

同桌之间说一说验证的方法和结果。

学生探究长方形和正方形的边和角的特征。

两位教师都基于学生已有知识展开教学，从学生的作品中入手，通过师生互动、质疑等方式探究出四边形有4条边和4个角。不同的是，李老师更注重让学生抽象出四边形的定义，而郑老师更关注对特征的描述。但两位教师的设计都只是从四边形作为一个独立的图形类型进入，忽略了平面图形与立体图形之间的联系，也忽略了四边形立足于平面图形的特殊地位。郑老师设计了四边形的进一步分类和探究长方形、正方形的特征，看上去让整个四边形的学习内容更加充实，但也显示出课的容量过大，课堂的重心发生偏移。

延展：如何能够使得一节课只上到四边形的认识又不显得课的内容过于单薄？如何继续采用分类，又避免出现非核心图形出现干扰？

2. 在不同的教材中探索

为了寻求将图形的认识结构放大的有力支撑，笔者精心阅读了三个版本的教材，发现它们在编排上有所差异，但在知识形成体系上却有着异曲同工之处，都经历了从立体图形到平面图形，从四边形到特殊四边形的要素特征学习，再到四边形和三角形的内部特征学习。

而在深入读教材的过程中，笔者欣喜地发现了自己一直在寻求的“结构化”教学的最佳佐证——北师大版和苏教版在分类时，都将三角形纳入其中，从“边”和“角”的角度对图形作进一步的认识，并根据“边”和“角”进行分类和命名。而苏教版更加大胆地将四边形往多边形进行了拓展，使平面图形的结构更加完善。

小学阶段的图形认识应该是从直观认识到要素认识，从类型认识再到特征认识，体现的是由一个图形外部向图形内部的认识过程，从一般物体形状的认识到长方体与正方体的认识，从一般三角形与四边形的认识到长方形与正方形的认识再到平行四边形与梯形的认识，体现的是一个从上位的一般图形到下位的特殊图形的认识过程。三个版本的教材各有特点，总体来说，苏教版的教材在这一内容上的编排更符合学生的认知发展规律，因此在教学这一内容时值得借鉴。

何以延展：学会从分类的角度来研究图形是本课的目标之一，分类仅仅分四边形吗？是否可以把结构放大，视野更加宽泛地帮助学生在平面图形要素特征研究的第一课时建立平面图形世界的网络呢？

三、完善与重建——四边形的认识“结构化教学”的延展

就“三角形与四边形认识”的教学而言，主要的教学任务是帮助学生认识图形构成的基本要素“边”和“角”，并从“边”和“角”的角度来判断认识图形，这些要素是学生认识研究图形的上位的学习方法结构，学生从这些角度展开几何图形的认识、发现、论证和获得结论的研究活动。基于以上思考，本节课基于学生的现实基础在分类活动中初步建立几何图形概念的初步理解。

（一）整体进入，建立结构

整体进入，可以理解为从整体上对学习内容有初步的感悟和体验，为学生发现问题、研究问题和形成新知识提供了脚手架式的结构支撑。一年级时学习过的立体图形的知识为这节课提供了先行组织者，使得学生更深刻地体会到面在体上，同时与前知对接。

为了帮助学生经历三角形与四边形的概念形成过程，由学生在一年级便学过的生活中常见的立体图形作为突破口，再由立体图形到平面图形，让学生体会面在体上，与前面学过的知识进行连接。这样的问题找准了学生的知识生长点，联系了学生的已有经验。而这些平面图形中有围成的，也有不围成的，从中抽象出封闭图形和不封闭图形的概念。图形认识的一般过程是从一般的图形到特殊的图形的认识过程。由立体图形的一个面可以抽象出平面图形，接着将平面图形分成封闭图形和不封闭图形两类，初步建立结构。

（二）要素认识，运用结构

接着在封闭图形中根据边的曲直分成了都是直边的图形和有曲边的图形两类。直边图形中根据边的数量或者角的数量可以分成三角形、四边形，由此认识了图形的基本要素“边”和“角”，并能从“边”和“角”的角度来判断认识图形。第一次认识的时候教会学生结构，后续的认识图形就是学生运用所学的“边”和“角”去进行三角形和四边形的命名。同时拓展开去，如果有5条直边5个角的图形呢？有6条直边6个角的图形呢？将三角形和四边形的研究范圍拓展到多边形。

（三）经历分类，体验过程

通过几次分类，让学生聚焦三角形和四边形的本质属性，在巩固练习阶段，让学生经历从辨一辨、画一画进而到添一添的过程，由辨一辨到画一画的阶段正是让学生运用所学知识进一步体会三角形和四边形的本质特征，而添一添也正是让学生运用分类思想，添上一条线段，如何添？可以将情况分为由顶点出发的，由边出发的。那么在由顶点出发的情况中，又可以分为从顶点到顶点，从顶点到边。由边出发的可能性中，又可以分成从边到对边和从边到邻边的这两种情况。进一步让学生运用分类思想，运用结构去添一添。

《四边形的认识》一课，源于“结构化”，却又在如何更好地“结构化”过程中，通过类比、分析、借鉴寻求到课堂教学延展的宝贵资源。这样的探寻，不仅使教师对整个知识结构更加了然于胸，更让学生能以一种结构化的眼光去对待所学的知识，并形成学习的方法。

参考文献

[1]侯正海.“图形的认识”教学中的几个关键问题[J].小学数学教育，2018（Z4）.

[2]吴亚萍.数学教学改革指导纲要[M].福州：福建教育出版社，2017.

[3]徐冰，魏瑞霞.“四边形的认识”教学实录与评析[J].小学数学教育，2018（21）.

（浙江省宁波市镇海兆龙学校，宁波 315000）