钢管混凝土组合柱受剪承载力分析模型

2021-06-10柯晓军

工程科学与技术 2021年3期

柯晓军，丁文

(1.广西大学土木建筑工程学院，广西南宁 530004；2.广西大学工程防灾与结构安全教育部重点实验室，广西南宁 530004)

钢管混凝土组合柱是钢筋混凝土柱中内置同期浇筑的钢管混凝土柱而组成的一种组合构件[1]。目前国内外学者对钢管混凝土组合柱受压[2–3]、受拉[4]、抗震性能[5–6]及长期性能[7–8]等方面进行了系列研究。研究表明：适当提高组合柱的体积配箍率、配箍形式、钢管套箍指标等参数能有效改善钢管混凝土组合柱管内外组成部分协调工作能力，提高其各项力学性能。由于钢材与混凝土力学性能上的差异、钢管与混凝土之间相互作用，导致组合柱的界面传力及破坏模式复杂[9]，有关钢管混凝土组合柱受剪性能及受剪承载力的模型化建立与计算方法研究较为缺乏，已有研究的也都是基于有限试验数据拟合得到的，适用范围有待验证。因此，进行受剪承载力计算理论的研究是非常有必要的。

现阶段，为预测界面受力复杂的组合构件受剪承载力，许多学者尝试运用钢筋混凝土结构中的受剪理论进行分析。邓明科等[10]基于拉–压杆模型，建立了能够反映型钢混凝土深梁受剪传力机制和破坏模式的承载力计算模型；Waleed等[11]基于拉–压杆模型，提出了方钢管混凝土梁受剪承载力计算方法；魏建萍等[12]根据桁架–拱模型，考虑型钢腹板和翼缘对混凝土抗剪的有利作用，推导出实腹式型钢混凝土短柱受剪承载力计算公式；朱伟庆[13]、王震[14]等基于修正压力场理论，建立了型钢混凝土柱、方钢管混凝土柱的受剪承载力计算模型；杨勇等[15]基于桁架–斜压场理论，推导出方钢管混凝土叠合构件的受剪承载力计算公式。上述研究表明，采用钢筋混凝土结构中相对成熟的受剪理论，对型钢（钢管）混凝土构件、叠合构件的受剪承载力进行分析与计算是可行的。

作者在通过试验揭示钢管混凝土组合柱特性的基础上，对桁架–斜压场模型进行修正，提出相应的受剪承载力计算方法，并与中国现行规范、美国规范AISC[16]、欧洲规范EC4[17]中受剪承载力计算方法进行对比，最后分析剪跨比、体积配箍率、混凝土抗压强度、轴压比、套箍指标及钢管径厚比对计算模型的影响。

1 试验概况

文献[18]设计11根钢管混凝土组合柱进行受剪性能试验，主要考虑剪跨比、体积配箍率、箍筋形式、轴压比、钢管尺寸的影响，构件参数详见表1。

截面尺寸b×h=250 mm×250 mm，截面配筋见图1；试验采用商品混凝土，预留标准立方体的实测抗压强度为78 MPa；采用Q235级有缝钢管，钢管直径为140和114 mm，实测屈服强度分别为361和410 MPa；纵筋、箍筋分别采用直径10和6 mm的HRB400热轧钢筋，实测屈服强度为458和446 MPa。试验采用简支梁式加载，如图2所示。构件的破坏形态分为剪切黏结破坏、斜压破坏两种，如图3所示。

表1 构件设计参数和部分试验结果[18]Tab. 1 Design parameters and partial test results of specimens[18]

2 基于桁架–斜压场理论的承载力计算

由于钢管混凝土组合柱中钢管内外混凝土的约束条件有差异，因此，将组合柱构件分为管外箍筋约束混凝土部分与钢管内部约束部分进行分析。

文献[15]基于桁架–斜压场理论，建立了方钢管混凝土叠合构件的受剪承载力计算模型，但是模型建立时并未考虑工程实际中存在的轴压力作用，以及钢管约束作用对混凝土强度的提高，因此需要调整模型受力条件，获得相应的修正计算公式。

图1 构件截面配筋Fig. 1 Reinforcement of specimen cross section

图2 试验加载示意图Fig. 2 Schematic diagram of test set-up

图3 构件破坏形态Fig. 3 Failure patterns of specimens

桁架–斜压场理论的基本假定：1）钢管内外混凝土不承受拉力；2）不考虑纵筋销栓作用对试件抗剪承载力的影响；3）构件承载力达到极限状态时，箍筋屈服，钢管外混凝土因桁架作用和斜压场作用达到抗压强度。

组合柱构件受剪承载力由箍筋Vs、混凝土Vc、钢管Va共3部分承受。即：

2.1 箍筋受剪承载力Vs

图4为桁架模型示意图。图4（a）中试件上、下部纵筋分别为受压、受拉弦杆；箍筋为竖杆，承受竖向拉力；裂缝间混凝土为受压斜腹杆[19]。为了简化计算，假定构件斜裂缝平行发展（图4（b）），根据受力平衡条件可知：

图4 桁架模型示意图Fig. 4 Schematic diagram of truss model

式中：σc为混凝土开裂后裂缝间混凝土斜腹杆中的应力；bw、j分别为截面有效宽度、高度；φ为斜裂缝倾角，根据试件实际裂缝情况取为40°；fyv为箍筋的屈服强度；Asv为单肢箍横截面面积。

2.2 混凝土受剪承载力Vc

由于钢管内外混凝土的约束条件不同，为了简化计算，将外径为D的圆钢管等效为边长为D、厚度不变的方钢管，构件截面划分为3个部分（图5），区域1、3为管外箍筋约束混凝土，区域2为钢管约束混凝土。构件中，混凝土部分受剪承载力分别为区域1混凝土Vc1、区域2混凝土Vc2、区域3混凝土Vc3这3部分剪力之和，即：

图5 截面等效与区域划分Fig. 5 Section equivalence and area division

图6为3部分混凝土的斜压场受力模型。构件破坏时混凝土受压强度为σa，σa=fce–σc[15]，根据式（5）可得：

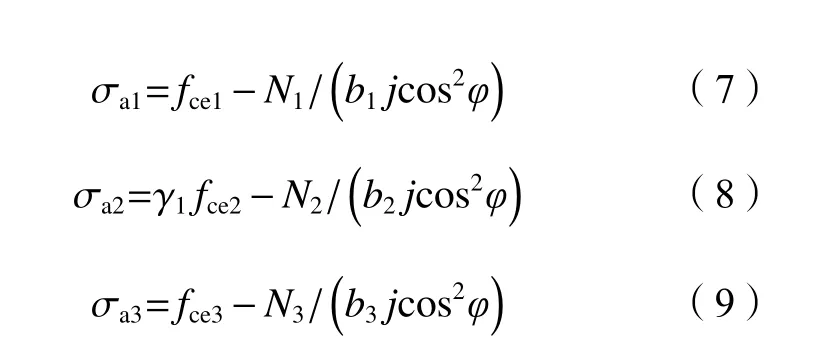
图6 混凝土斜压场受力模型Fig. 6 Force model of concrete oblique pressure field

式中：fce1、fce3为管外混凝土抗压强度；fce2为管内混凝土抗压强度；b1为钢管左右侧混凝土宽度，b1=b–D；b2为钢管内混凝土宽度，b2=D；b3为钢管上下侧混凝土宽度，b3=h–D；σa1、σa2、σa3和N1、N2、N3分别为3部分混凝土的受压强度与承受的轴压力。本文试验表明，构件发生斜压破坏时，管外混凝土均达到抗压强度，因此σa1=σa3=fce。

根据《钢管混凝土叠合柱结构技术规程》（T/CECS 188—2019），截面中3部分混凝土对应承担的轴力N1、N2、N3与各自轴压刚度有关，管内混凝土考虑到钢管约束对核心混凝土强度的提高，即：

式中：Eco、Aco分别为管外混凝土弹性模量及截面面积；Ecc、Acc分别为管内混凝土弹性模量及截面面积；A1、A2、A3分别为3部分混凝土的面积；Ea、fa分别为钢管的弹性模型和屈服强度；γ1为套箍作用对混凝土强度的提高系数，与混凝土强度和套箍指标有关；β为混凝土强度影响系数，当混凝土强度等级不大于C50时，β=2.0，当混凝土强度等级大于C50时，β=1.8。

根据图6中的竖向力平衡条件可得，截面各部分的受剪承载力为：

式中：η=fyvρsv(1+cot2φ)[b/(b–b3)]/σc[15]；ω、α分别为斜压带的宽度与纵向倾角，ω按式（17）计算：

式中：la、lc分别为上、下垫块的宽度；lb、ld分别为压杆顶部、底部节点区高度，lb=2(h–h0)，h0为截面有效高度，ld=0.4kh0，k为弯矩作用下混凝土受压区高度系数[20]，对于区域2、3，lb=ld=0。

2.3 钢管受剪承载力Va

根据《组合结构设计规范》（JGJ 138—2016），考虑轴向压力对钢管受剪承载力影响的计算公式，即：

综上，基于修正桁架–斜压场模型，所建立的受剪承载力计算方法见式（19）：

3 计算方法的验证与分析

在文献[18]的试验基础上，补充收集到25根钢管混凝土组合柱的受剪性能试验资料[21]。文献[21]中试验参数：截面尺寸为200 mm×200 mm，fyv为235 MPa，λ为0.75～1.45，fcu为81.2～100.5 MPa，ρv为0.90%～1.79%，轴压比为0.384～0.513；钢管外径为54、65、80 mm 3种规格，壁厚均为2 mm，实测屈服强度分别为381、367、352 MPa。

3.1 模型与规范方法计算结果对比

基于36组试验数据，对本文建立的计算方法进行验证，并与中国规范T/CECS 188、美国规范AISC及欧洲规范EC4的计算方法加以对比，计算结果如图7所示。图7中，Vu1、Vu2、Vu3、Vu4分别为采用修正桁架–斜压场模型、T/CECS188、AISC和EC4规范计算的受剪承载力值。

图7 不同理论预测的受剪承载力Fig. 7 Shear bearing capacity predicted by different modulus

由图7可知：

1）采用修正桁架–斜压场模型计算的构件受剪承载力与试验值的比值均值为0.996，标准差为0.085，变异系数为0.085。表明在轴压力作用下，将圆钢管等效为方钢管后的修正桁架–斜压场模型，可较好地预测钢管混凝土组合柱的受剪承载力。

2）采用中国规范T/CECS 188—2019计算的构件受剪承载力与试验值比值的平均值为0.898，标准差为0.090，变异系数为0.100。同时，观察到计算值普遍低于试验值，虽有一定的安全裕度，但精度不足。

3）采用美国AISC和欧洲EC4规范的计算值与试验值比值的平均值分别为0.964、0.928；标准差为0.163、0.158；变异系数为0.169、0.170。总体上来说，计算值与试验值离散型较大。当剪跨比大于1.4时，采用AISC规范计算偏于不安全。

造成现行规范计算结果偏差较大的原因，是因为中国规范T/CECS 188、美国规范AISC和欧洲规范EC4的计算方法，虽能在一定程度上反映混凝土强度、箍筋、轴压力和剪跨比对钢管混凝土组合柱抗剪承载力的贡献，但并未考虑箍筋与钢管约束作用对混凝土强度的提高，以及组合柱各组成部分之间相互作用的影响；二是当组合柱达到峰值承载力时，管内混凝土并未达到抗拉强度极限，该因素在上述规范计算方法也未能得到考虑，因此计算结果误差较大，

3.2 计算模型的敏感性分析

以剪跨比λ、体积配箍率ρv、混凝土强度fc、轴压比nd、套箍指标θ及钢管径厚比D/t为变化参数，分析比较修正后的桁架–斜压场模型的计算值与试验值的比值与各影响参数的变化关系如图8所示。由图8中变化参数分析结果可知，本文提出的计算模型对剪跨比、体积配箍率、混凝土强度、轴压比、套箍指标及钢管径厚比的反映均较为稳定，各参数的变化对模型计算精度影响不大，计算值与试验值的比值范围在0.85～1.15之间，说明模型能较好反映各参数对试件的抗剪承载力影响，计算模型在所验算的试验参数值范围内具有很好的适用性。