考虑温度和冻融循环的基桩水平承载特性研究
2021-06-10尹平保杨铠波杨朝晖
尹平保,杨铠波,杨朝晖,3,贺 炜,余 伟
(1.长沙理工大学 土木工程学院,湖南 长沙 410114;2.长沙理工大学 南方地区桥梁长期性能提升技术国家地方工程实验室,湖南 长沙 410114;3.阿拉斯加大学 工程学院,阿拉斯加州 安克雷奇 99508)
随着中国“一带一路”及“振兴东北老工业基地”等国家战略方针的实施和推进,越来越多的高速公路或铁路需向寒区延伸,从而导致许多桩基设置在多年或季节性冻土中(如西藏、青海、甘肃、新疆、内蒙古、四川、黑龙江、吉林、辽宁及河北等地区)。实际工程调研发现,寒区桩基工程病害频发,其原因在于温度变化和冻融循环作用将影响寒区桩周土体的强度特性,进而导致桩基承载机理及破坏模式发生改变,由此带来的安全风险和经济损失,对于寒区桩基工程不容忽视[1–3]。
近年来,国内外部分学者对寒区桩基工程展开了相关研究。如:张建明等[4]通过室内模型试验研究了冻土单桩的沉降特性;邱明国等[5]通过均质冻土基桩破坏性试验,发现冻土桩的荷载–沉降曲线呈陡降型,其承载力由土体冻结强度控制;汪仁和等[6]开展了冻土单桩抗压静载试验,研究了不同冻结温度下冻土单桩的竖向承载特性,获得了基桩冻结力、竖向承载力与温度之间的关系式;吴亚平等[7–8]通过室内模型试验,研究了桩身冻结力与桩端阻力之间的函数关系,探讨了循环荷载大小、加载频率及温度对桩土流变效应和竖向荷载传递规律的影响;孙飞翔[9]通过土体冻融循环试验,研究了冻融循环及温度对桩基竖向承载力的影响规律。但上述研究主要从竖向承载角度分析冻土与基桩的相互作用,大多数基桩除承受竖向荷载外,还将承受偏心力、风荷载及地震作用等水平荷载。为此,Suleiman等[10–11]开展了季节性冻土桩基大比例模型试验,分析了基桩的水平承载破坏模式;李永波等[12–13]开展了冻融条件下单桩水平动载试验,并基于动力BNWF模型,提出冻土桩基动力相互作用非线性反应分析方法;张嘉文等[14]开展了冻、融土中单桩水平静载试验,对比分析了不同温度和冻、融条件下单桩的变形与受力特性;杨润林等[15]通过冻土桩基地震响应振动台试验,研究了地震作用下冻土、液化土和桩的相互作用机理。以上研究主要从试验方面分析冻土桩基的水平承载特性,但在理论方面还不够完善,主要表现为:一是,尚未体现基桩与冻土水平相互作用特性;二是,未考虑冻结温度及冻融循环对基桩受力与变形的影响。
为此,基于现有研究,首先,通过试验反演得到冻土基桩p–y曲线及其与冻结温度、冻融循环次数之间的关系式;然后,根据基桩–冻土相互作用模型及差分理论,推求基桩受力与变形的理论解答,进而探讨冻结温度及冻融循环次数对基桩水平承载特性的影响。
1 基桩p–y曲线模型
1.1 考虑温度变化的冻土基桩p–y曲线模型
已有研究表明,当土体冻结后,其物理力学性质与弱岩或硬黏土相似,即其刚度和强度增幅较大[16–18]。因此,可对Reese[18]和Matlock[19]得到的p–y曲线进行修正,建立冻土地基p–y曲线,如图1所示。
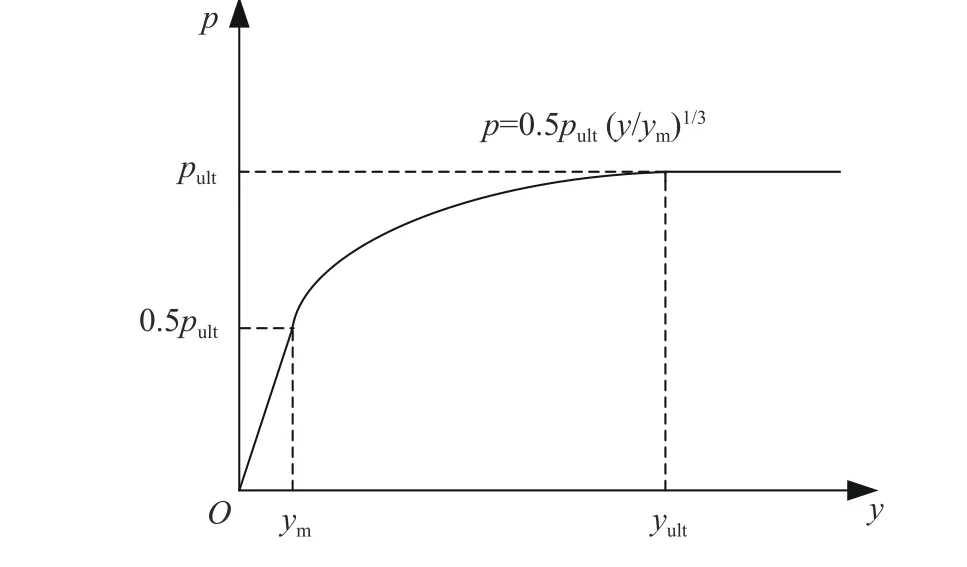
图1 冻土p−y曲线Fig. 1 p−y curve of frozen soil
图1中的冻土地基p–y曲线由两段组成:一是,当桩侧水平地基反力尚未达到极限(y≤yult)时,桩侧水平地基反力与桩身水平位移呈幂函数关系;二是,当桩侧水平地基反力达到极限(y>yult)后,桩侧水平地基反力即保持极限反力不变,其表达式为:
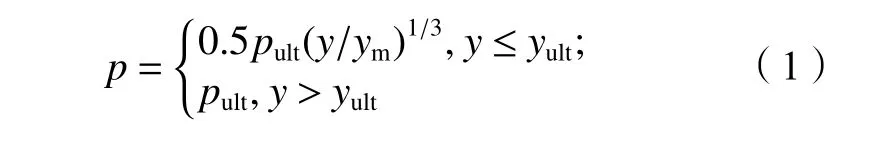
式中:p为水平地基反力;pult为水平地基极限反力;y为桩身水平位移;yult为水平地基极限反力达到极限时对应的桩身水平位移;ym为水平地基极限反力发挥一半时对应的桩身水平位移,其可以表示为:

式中:km为三轴剪切试验中主应力差达到最大主应力差一半时对应的轴向应变[19],即km=ε50,通常情况下可取km=ε50=1/25;D为桩径或桩宽。
土体冻结后强度将有显著提高,其工程特性类似于软弱岩石,故可利用Reese[18]提出的软弱岩地基的水平地基极限反力计算冻土地基的水平地基极限反力pult:

式中,qu为冻土单轴抗压强度,MPa。
Zhu和Carbee[20]通过试验研究发现深度z处冻土单轴抗压强度qu与温度T(z)之间的关系式为:

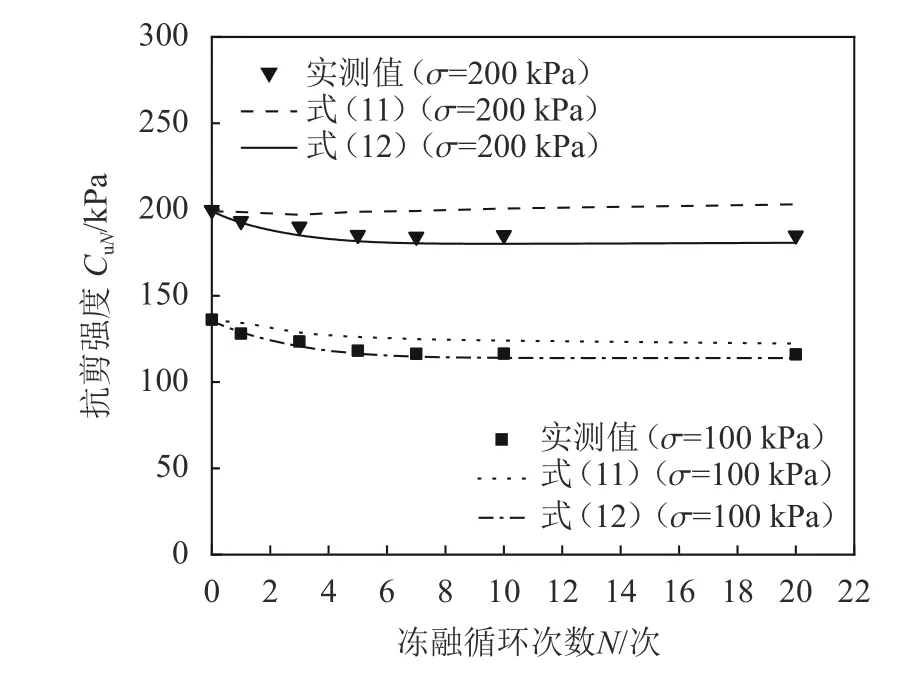
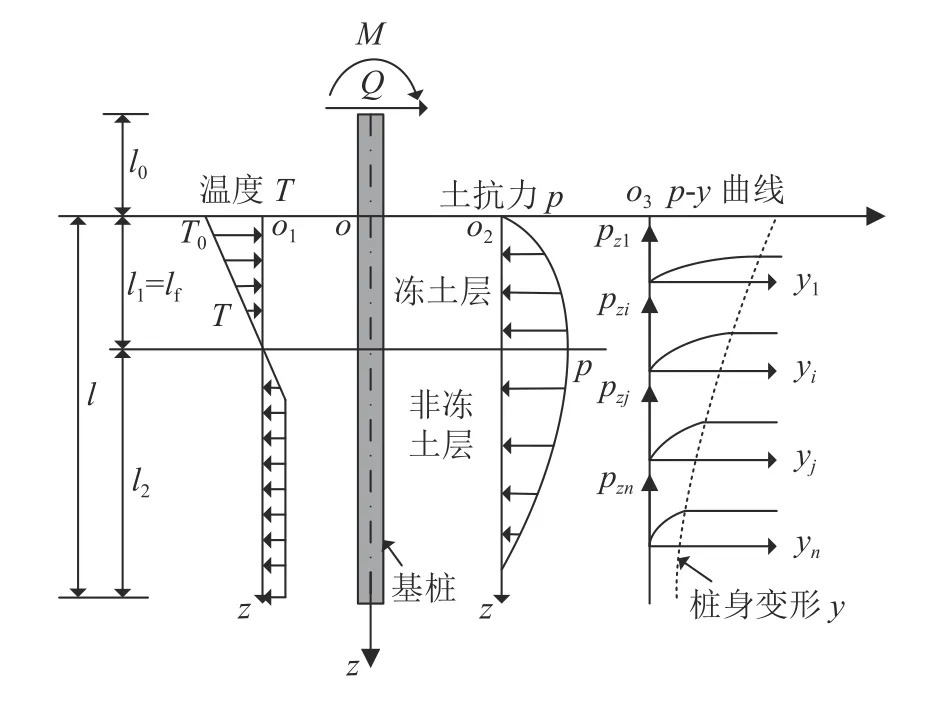
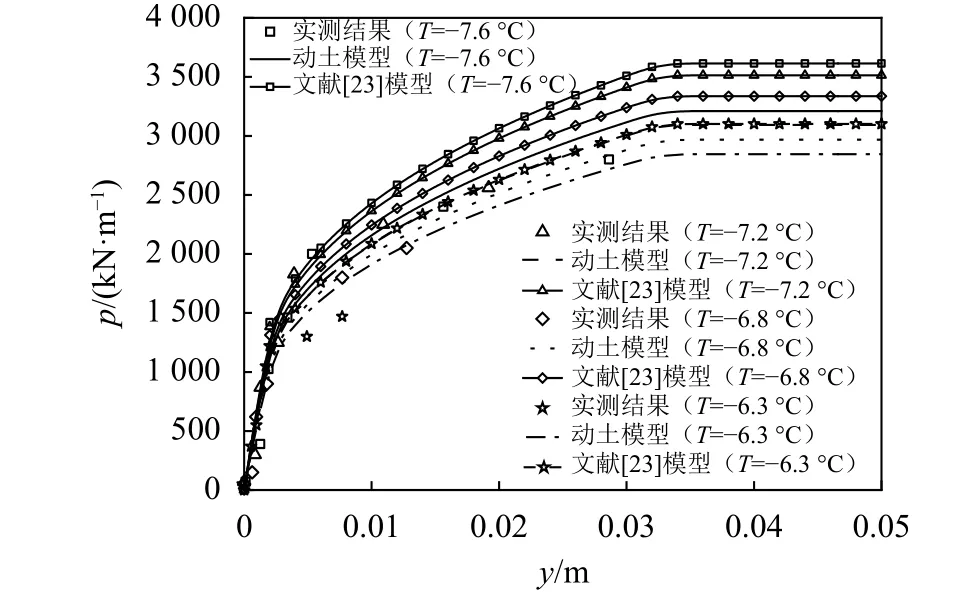
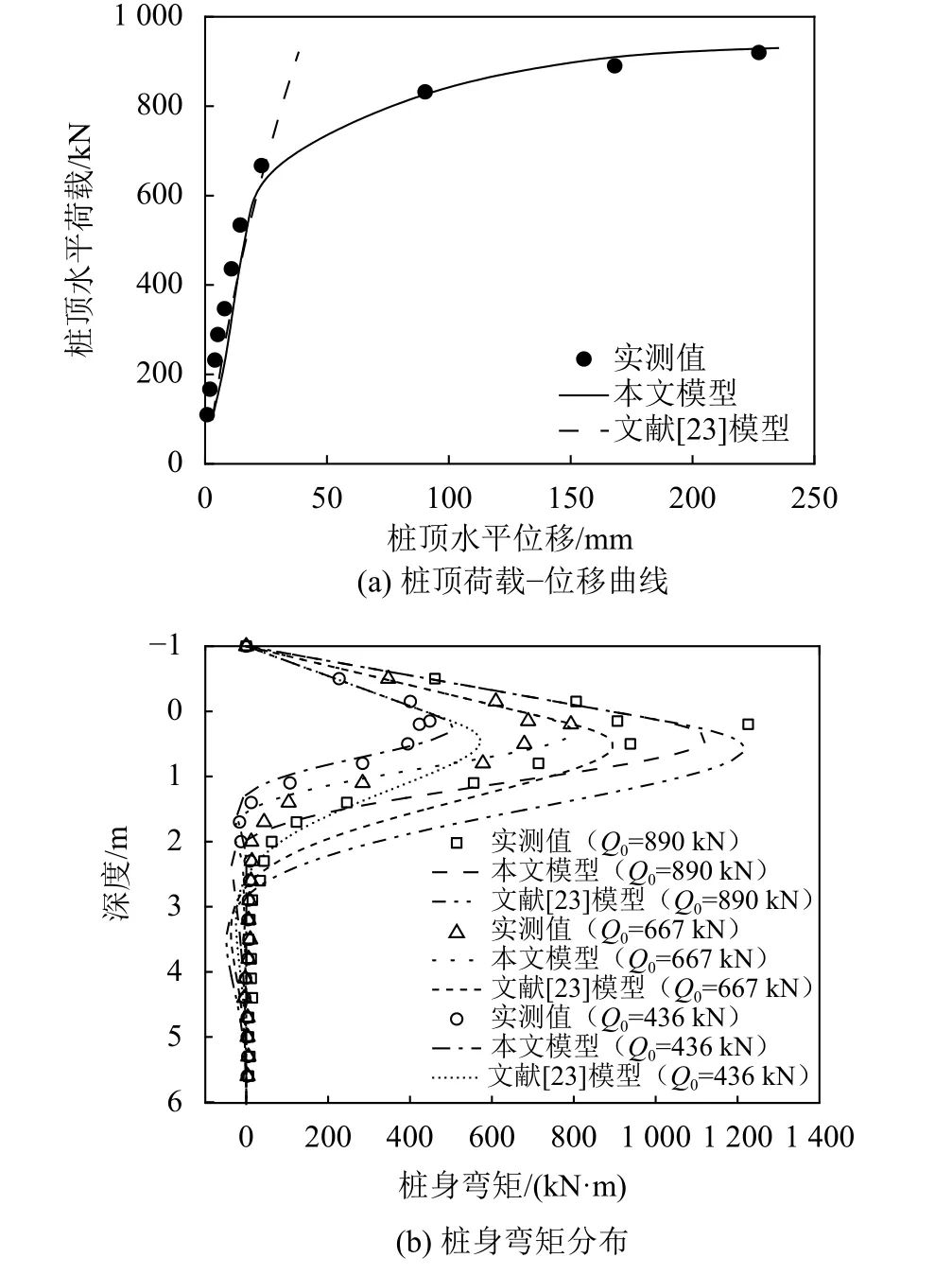
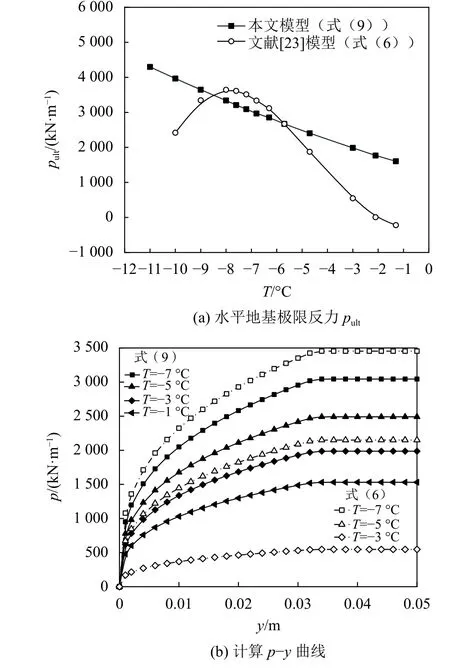
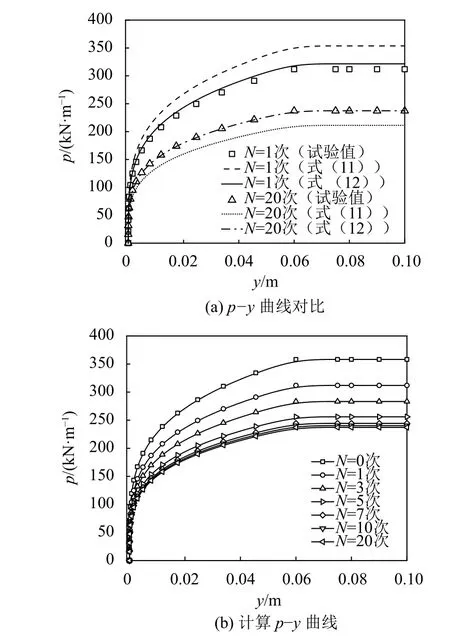
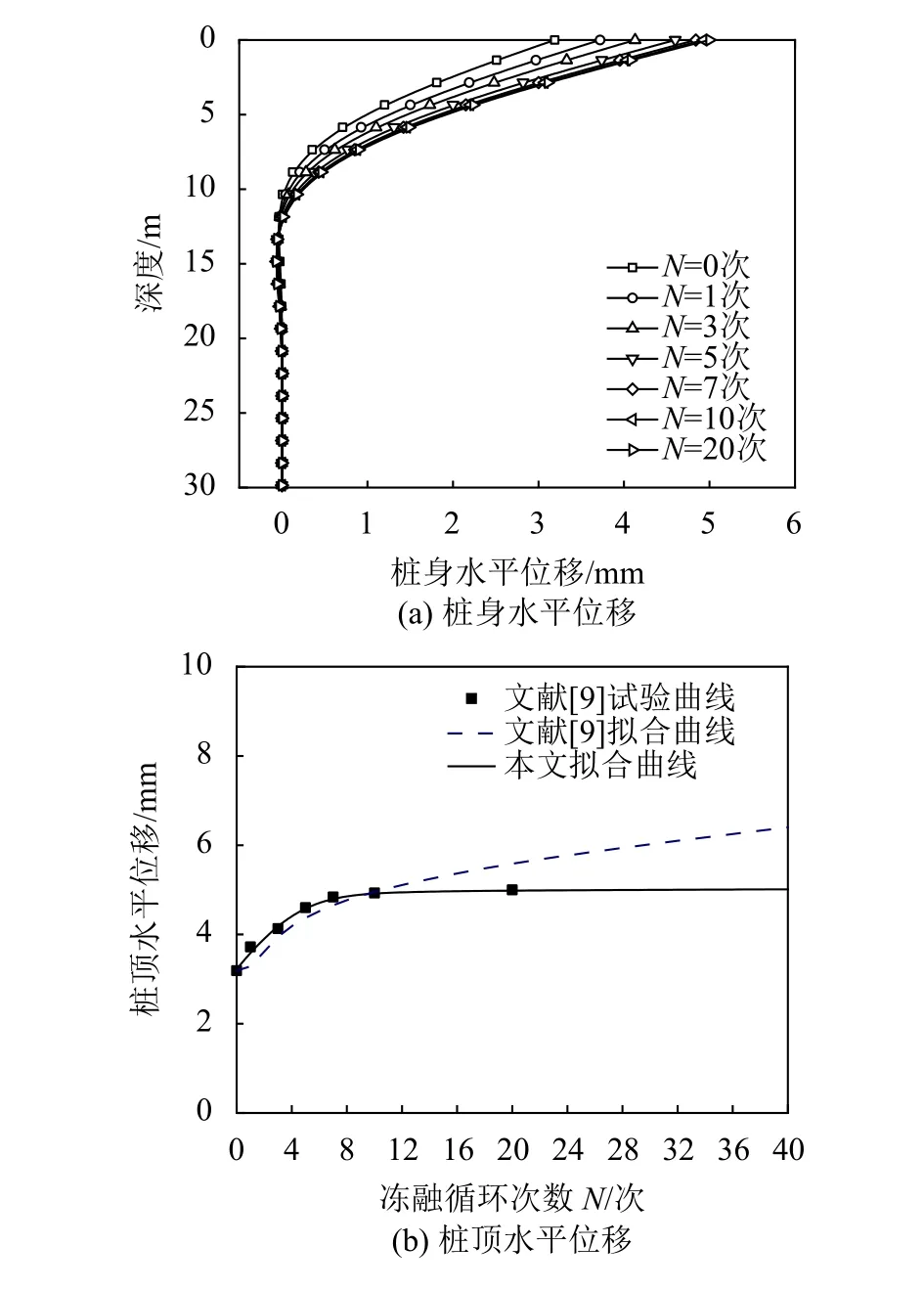
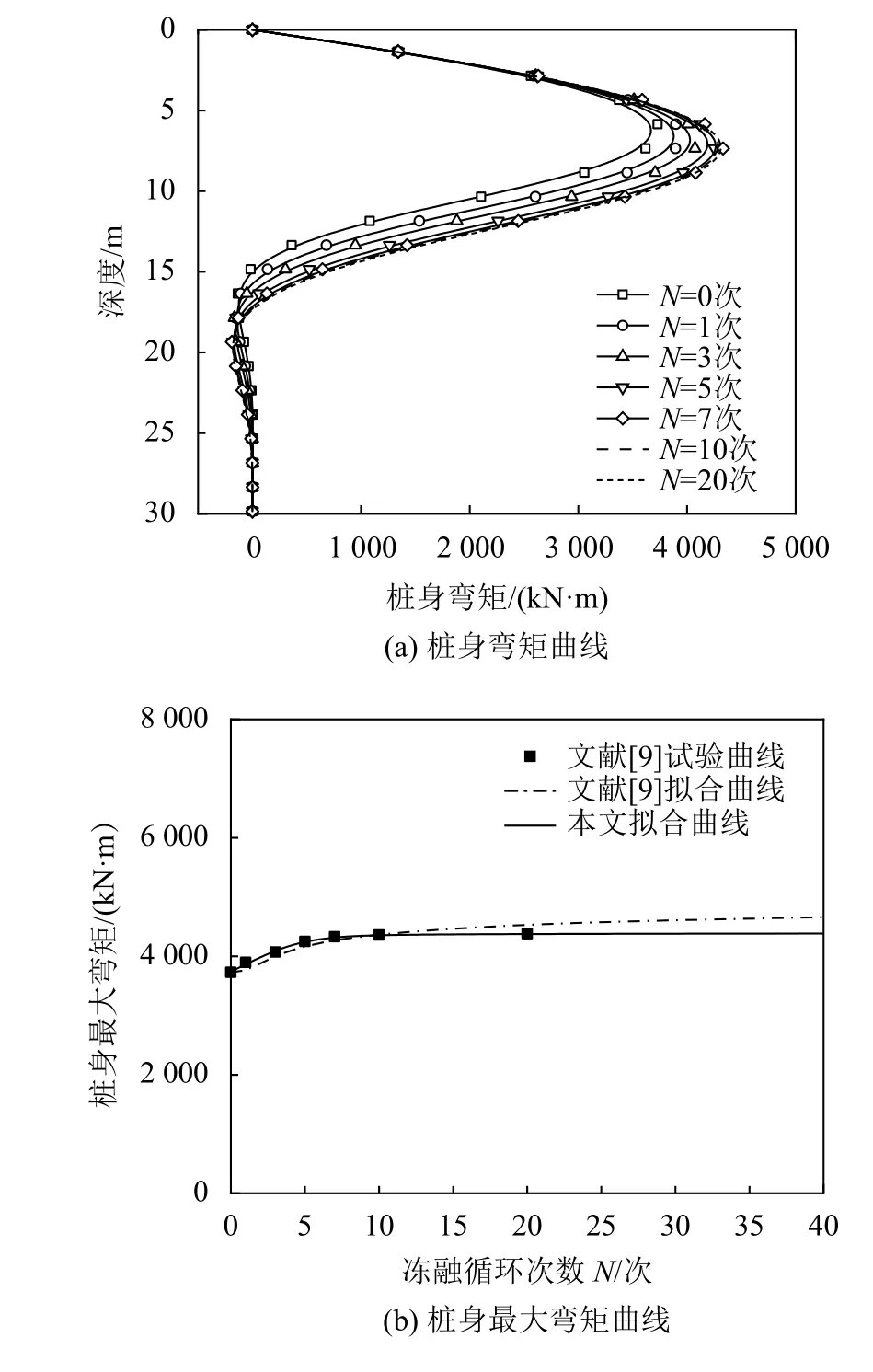
式中,T(z)为地面以下深度z处冻土温度,℃,–18 ℃ 式中:T0为地面处冻土温度;lf为地面以下冻土层厚度,即冻结厚度;z为 温度计算点埋深,0 同时,可以利用李永波等[13,23]建立的拟合公式计算冻土地基的水平地基极限反力pult: 其中,冻土单轴抗压强度qu与土体温度T间的关系为: 式中,T为冻土负温。 已有研究表明,土体经历冻融循环后,其内摩擦角增大,黏聚力降低[24–25]。这是因为冻融循环会导致土体内孔隙数量增加,重新排列的土颗粒具有更多接触点,有利于摩擦力的发挥;同时,冻融循环会破坏土体原有结构,使得其密度和土颗粒间的胶结力减小,故而黏聚力降低[26]。据此,可对式(1)中的ym和pult进行修正,从而建立考虑冻融循环的基桩p–y曲线模型。其中,ym表示为[19]: 式中,η为经验系数,一般情况下取2.5。 考虑冻融循环后的水平地基极限反力pult为: 式中:Cu为不排水抗剪强度值;γ为土体有效重度;zr为临界深度,其表达式为: 孙飞翔[9]通过试验,得到冻融循环后冻结土体不排水抗剪强度与冻融循环次数N之间的关系式为: 式中,CuN为经N次冻融循环后土体的不排水抗剪强度,c0为土体未经冻融循环的黏聚力,φ0为土体未经冻融循环的内摩擦角,N为冻融循环次数,σ为法向应力。 基于孙飞翔[9]的试验结果和多参数ExpAssoc函数,对式(11)进行修正,可得经N次冻融循环后土体不排水抗剪强度CuN的计算公式: 基于式(11)和(12)计算得到的土体不排水抗剪强度CuN值与文献[9]中的实测值对比如图2所示。 图2 实测值与拟合曲线对比Fig. 2 Comparison of measured values and fitted curves 由图2可知:由式(11)和(12)计算得到的土体经N次冻融循环后的不排水抗剪强度CuN值与实测值均吻合较好;相对而言,本文拟合公式(12)与实测值更接近。 根据水平荷载作用下冻土基桩变形、冻融循环后桩周土体水平抗力变化及场地温度分布规律,可建立图3所示的简化计算模型。 图3 冻土基桩简化计算模型Fig. 3 Simplified calculation model of piles in frozen ground 对于图3中的基桩,取其中的某一微元段进行受力分析,可建立水平荷载作用下基桩挠曲微分方程: 式中,EI为桩身抗弯刚度,其他参数同前。 实际工程中桩顶与桩端的边界条件主要有自由、嵌固和铰接等[27–28],假定桩顶自由,桩端嵌固。对于式(13)采用有限差分法进行求解。 首先,根据桩身受力、截面尺寸与刚度、桩周土层分布情况,将基桩分成n个桩段,如图3所示,可分为3段:第1段(l0)在地面以上、第2段(l1)在冻土层中、第3段(l2)在非冻土层中;然后,将每一桩段等长度离散为N个单元,每个单元长度为h=l/N,基桩各节点编号分别为0、1、2、 ···、N。根据中心差分原理在每一桩段的顶部和底部分别增设2个虚拟单元,其节点编号分别为–2、–1和N+1、N+2,相应地,可得离散后的桩身位移序列{yi},如图4所示。 图4 桩身挠曲及其差分点Fig. 4 Deflection and differential points of piles 根据中心差分原理可得基桩挠曲微分方程式(13)的差分格式为: 式中,h为每个桩段的单元长度。 桩端及桩顶边界条件差分格式分别为: 式中,M0为桩顶弯矩,Q0为桩顶剪力。 相邻桩段的交界面处还应满足位移、转角、弯矩和剪力相等的协调条件,其对应的差分格式为: 联立式(14)~(17),可建立相应的矩阵方程: 式中,K为桩身水平刚度矩阵,F为外荷载列向量。K与F分别为: 式中,λ=h4D/EI,A1、A2···An、An+1与桩身各节点土的初始地基反力模量及p–y曲线形式有关。 通过求解上述矩阵方程,可得到桩身各节点的水平位移yi,进而利用差分公式计算桩身各节点的转角βi、弯矩Mi及剪力Qi,具体的差分公式为: Horazdovsky和Hulsey等[29–30]在美国阿拉斯加州的费尔班克斯开展了冻土桩水平承载现场试验。试验桩为实心钢管混凝土桩,桩径D=0.41 m;钢管壁厚t=9.5 mm;基桩总长L=7.3 m,其中,地面以上长l0=1.2 m,土内深度l=6.1 m。试验场地自上而下依次为冻结粉土、非冻结粉土和多年冻土,如图5和6所示,具体计算参数见表1。 图5 冻土基桩布置示意图Fig. 5 Schematic diagram of pile in frozen ground 图6 冻土中的现场试验桩[29–30]Fig. 6 Field test pile in frozen ground[29–30] 表1 冻土基桩计算参数Tab. 1 Calculation parameters of the pile in frozen soil 计算得到的p–y曲线、荷载–位移曲线及桩身弯矩曲线如图7和8所示。 由图7可知:本文及文献[23]的冻土p–y曲线模型与实测结果均吻合较好,验证了考虑冻土温度变化的冻土桩p–y曲线模型是合理的。当T=–6.3 ℃时,本文模型与实测结果之间的误差为19.3%,文献[23]模型与实测结果之间的误差为30.1%。 图7 计算与实测p–y曲线对比Fig. 7 Comparison of measured and calculated p–y curves 图8 冻土桩水平承载试验与计算结果对比Fig. 8 Comparison of horizontal bearing test and calculation results of frozen soil pile 由图8可知:当桩顶水平荷载Q0=436、667和890 kN时,本文计算得到的桩顶水平位移分别为13.8、21.5和138.2 mm,与实测结果的计算误差分别为27.7%、–7.1%和17.8%;桩身最大弯矩分别为504.6、801.9和1 126.8 kN·m,相应的计算误差分别为12.5%、1.1%和–8.1%。同样地,基于文献[23]模型计算得到的桩顶水平位移分别为14.0、24.4及36.5 mm,与实测结果的计算误差分别为29.3%、5.3%及78.3%;桩身最大弯矩分别为573.2、898.1及1 218.0 kN·m,计算误差分别为27.8%、13.3%及–0.7%。由此可见,基于本文及文献[23]模型所得的计算结果与实测结果均吻合较好;相对而言,本文p–y曲线模型更能反映冻结温度与基桩受力与变形之间的关系。 为研究冻结温度对基桩受力与变形的影响,以第3.1节中的冻土基桩为例,进行影响因素分析,具体参数同前。通过将式(6)、(9)的计算结果代入式(1)计算,可得到不同冻结温度下、地面以下0.25 m处基桩的pult和p–y曲线如图9所示。 图9 不同冻结温度下 pult和 p–y 曲线Fig. 9 pult and p–y curves under different freezing temperatures 由图9(a)可知,地基水平极限反力pult随冻土温度升高而减小。当温度–9 ℃≤T≤–5 ℃时,由本文和文献[23]模型计算得到的水平地基极限反力pult值受温度影响不大,二者计算结果较接近;当温度T<–9 ℃或T>–5 ℃时,本文模型随温度呈线性发展,文献[23]模型随温度呈非线性发展。这是因为文献[23]模型中的冻土强度qu随温度呈非线性发展。结合图8中试验与计算结果可知,本文模型与实际情况更为接近,故文献[23]模型在–9 ℃≤T≤–5 ℃的温度区间与实测结果较吻合,当冻结温度超出该区间后,该模型计算误差较大。图9同时显示,在桩身水平位移y相同的情况下,水平地基反力p随冻结温度T降低而增大。 令桩顶水平荷载Q0=667 kN,可得不同冻结温度T下,基桩位移和弯矩变化曲线,如图10所示。 图10 不同冻结温度下基桩位移和弯矩变化Fig. 10 Displacement and bending moment under different freezing temperature 由图10可知,桩周土体冻结温度T越低,桩身水平位移及弯矩均越小。当T>–5 ℃时,桩身内力与位移受冻结温度的影响较大;当冻结温度T≤–5 ℃时,桩身内力与位移受冻结温度的影响越来越小。当T=–1 ℃、–5 ℃、–9 ℃时,基于本文冻土p–y曲线模型计算得到的桩顶水平位移分别为33.4 mm、29.2 mm和25.3 mm,T=–5 ℃、–9 ℃的桩顶水平位移较T=–1 ℃时分别减小了12.6%、13.4%;桩身最大弯矩分别为982 kN·m、913 kN·m和889 kN·m,T=–5、–9 ℃对应的桩身最大弯矩较T=–1 ℃时分别减小了7.0%和2.6%。而由文献[23]模型计算得到相应温度下的桩顶水平位移分别为43.5 mm、29.2 mm和25.1 mm,较T=–1 ℃分别减小了32.9%、14.1%;桩身最大弯矩为1 142 kN·m、934 kN·m和894 kN·m,较T=–1 ℃分别减小了18.2%、4.3%。 为探索冻融循环作用对基桩受力与变形的影响,以文献[9]中的查拉坪大桥基桩为例进行计算分析。该基桩桩周为粉土,桩径D=1.5 m;桩长L=30.0 m,其中,地面以上长l0=1.0 m,土内深度l=29.0 m,具体计算参数见表2。 表2 基桩计算参数Tab. 2 Calculation parameters of the pile 由式(11)、(12)代入式(1)可得冻融循环次数分别为1和20时,深度为0.5 m处的基桩p–y曲线,其与试验值对比如图11(a)所示;将式(12)代入式(1)可得不同冻融循环次数下,深度为0.5 m处的基桩p–y曲线,如图11(b)所示。 由图11(a)可知,由本文拟合公式(12)和由文献[9]得到的拟合公式(11)所得的p–y曲线均与试验曲线吻合较好。相对而言,本文p–y曲线与试验曲线更为接近。由图11(b)可知:在桩身水平位移y相同的情况下,水平地基反力p随冻融循环次数N增加而减小;当N≥7后,冻融循环对基桩p–y曲线的影响已不太明显。 令桩顶荷载Q0=1 000 kN,可得不同冻融循环次数下基桩水平位移及弯矩曲线,如图12和13所示。 图11 不同冻融循环次数下基桩p–y曲线Fig. 11 p–y curves under different freeze-thaw cycles 图12 不同冻融循环下基桩水平位移Fig. 12 Horizontal displacements of piles under different freeze-thaw cycles 图13 不同冻融循环下桩身弯矩Fig. 13 Bending moments of pile under different freezethaw cycles 由图12和13可知:当冻融循环次数N<7次时,桩身水平位移与弯矩均随冻融循环次数的增加呈非线性关系增大;当N≥7时,桩身水平位移与弯矩几乎保持不变,即冻融循环作用对基桩受力与变形的影响已不明显。当N=0和7时,基于本文拟合曲线计算得到的桩顶水平位移分别为3.19和4.84 mm,后者较前者增幅为51.7%;桩身最大弯矩分别为3 730和4 331 kN·m,增幅为16.1%;当N=20时,桩顶水平位移为5.01 mm,桩身最大弯矩为4 380 kN·m,与N=7相比,桩顶水平位移和桩身最大弯矩增幅分别为3.5%和1.1%。可见,当桩周土体经历7次冻融循环后,其对基桩受力与变形的影响可忽略不计。这是因为桩周土体在经历7次以上冻融循环之后,其抗剪强度指标(黏聚力和内摩擦角)不再随冻融循环次数增加而显著改变[25,31–33]。因此,为确保季节性冻土区桩基的安全稳定,在桩基设计时,建议至少考虑7~10次冻融循环对基桩受力与变形的影响。 基于已有试验,建立了考虑温度和冻融循环作用的基桩p–y曲线模型,推导了水平荷载作用下冻土基桩桩身内力与位移计算的有限差分解答,并将其与试验结果进行对比,进而探讨了温度及冻融循环次数对基桩受力与变形的影响,得到主要结论如下: 1)考虑温度沿深度呈线性变化的冻土p–y曲线与实测结果更为接近,更能反映冻结温度与基桩受力与变形之间的关系。冻结温度T越低,桩身水平位移及弯矩均越小,当T>–5 ℃时,桩身内力与位移受冻结温度的影响较大;当冻结温度T≤–5 ℃时,桩身内力与位移受冻结温度的影响越来越小。 2)当冻融循环次数N<7时,桩身水平位移和弯矩均随冻融循环次数的增加呈非线性关系增大。桩周土体经历7次冻融循环后,其桩顶水平位移和桩身最大弯矩分别增大51.7%和16.1%;当冻融循环次数N≥7后,桩身水平位移与弯矩受冻融循环次数的影响已不明显。 综上所述,温度变化和冻融循环作用对季节性冻土区桩基受力和变形的影响不容忽视。工程设计时,建议至少考虑7~10次冻融循环作用对桩基水平承载特性的影响。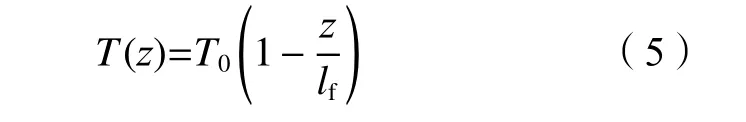
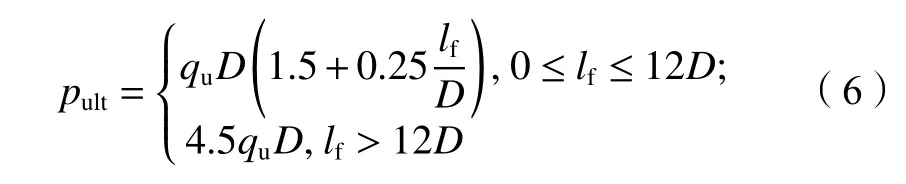
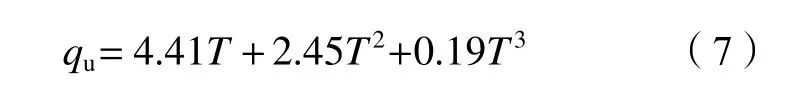
1.2 考虑冻融循环的基桩p–y曲线模型

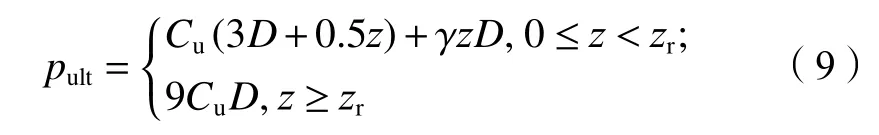
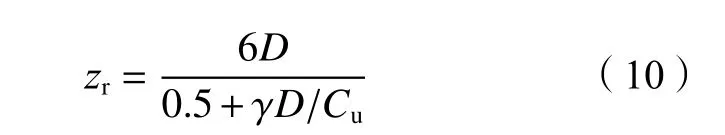
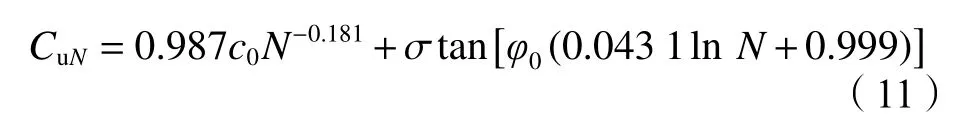
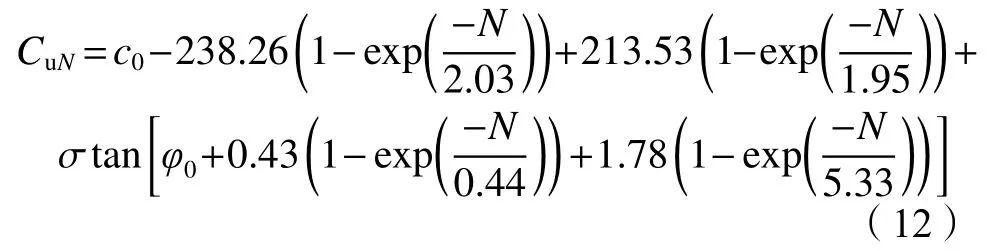
2 考虑冻融循环的基桩非线性分析
2.1 简化计算模型及方程建立
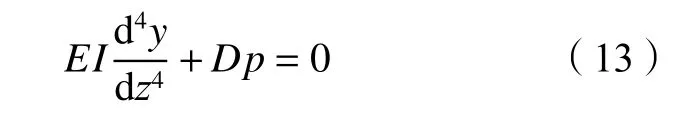
2.2 非线性分析理论解答

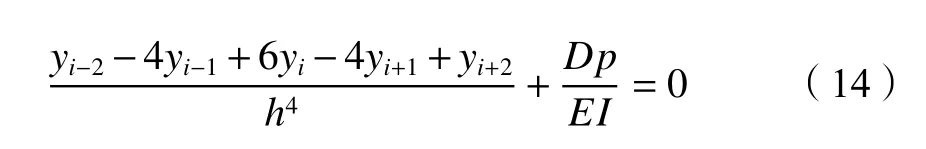
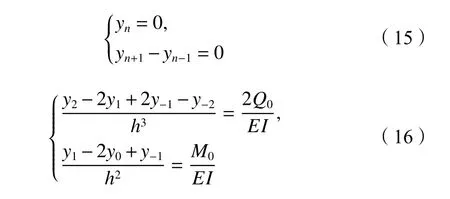
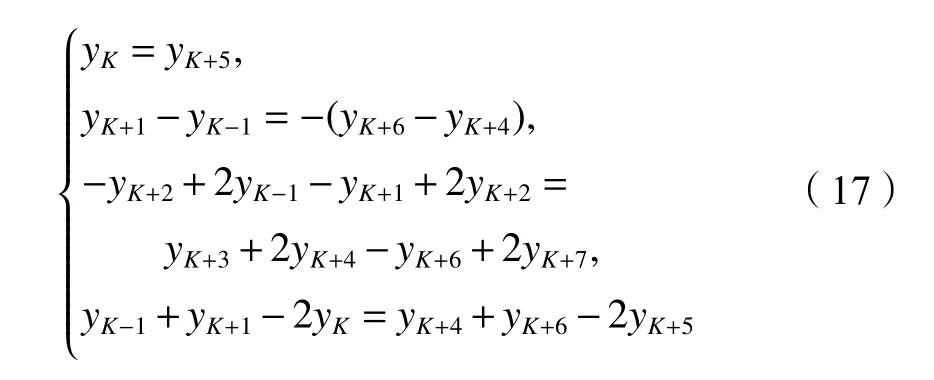


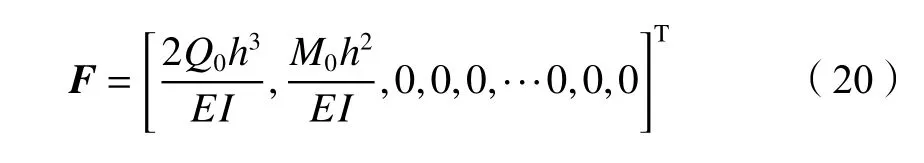

3 试验对比及影响因素分析
3.1 冻土基桩试验对比分析


3.2 冻结温度T对基桩水平承载特性的影响

3.3 冻融循环对基桩水平承载特性的影响

4 结 论
