考虑钢–砼接触特征的CFST管节点热点应力分析
2021-06-10吴琛泰
卫 星,吴琛泰,肖 林,李 俊
(西南交通大学 土木工程学院,四川 成都 610031)
由于良好的受力性能,钢管混凝土桁架自20世纪90年代以来,较多地应用于大跨度拱桥,近年来在梁式桥中也有不少应用。钢管混凝土桁架结构中,各组成管件交汇于相贯节点,相贯节点的力学性能需要特别关注。采用焊接连接的管节点结构复杂、受力复杂、焊缝形式特殊,是钢管桁架结构承载的重要部位,也是容易发生疲劳开裂的薄弱部位。对于钢管混凝土桁架桥梁,在服役期间承受车辆荷载反复作用,因此,近几年,在国内已建成的钢管混凝土桁架桥梁中疲劳问题日渐凸显[1–2]。这对钢管混凝土桁架结构桥梁的设计、运营管养及性能评价带来了新的问题。
中国现行的《公路钢管混凝土拱桥设计规范》(JTG/T D65–06—2015)[3]中,管节点疲劳设计仍采用基于名义应力的S–N曲线方法,该方法避开复杂的应力集中效应,较保守地低估了部分节点实际疲劳强度。同时,规范中对名义应力的取值位置也没有明确规定,若名义应力取值不当,节点的疲劳性能评估结果会产生较大差别。基于热点应力的S–N方法在复杂性和精确性上做到了很好的平衡,已在海洋平台等结构疲劳设计中得到普遍应用。管节点疲劳裂纹较多地起始于相贯焊缝的焊趾,国际焊接协会(ⅡW)推荐采用基于热点应力的S–N曲线对焊接管节点疲劳性能进行评估[4]。应力集中是影响焊接管节点疲劳行为的主要因素之一,研究沿焊趾的热点应力集中系数(HSCF)分布是基于热点应力方法开展钢管混凝土桁架焊接管节点疲劳行为研究的前提。通常习惯采用表征管节点几何特征的无量纲参数(如管径比、径长比、壁厚比等)建立能描述应力集中系数的复杂函数,如图1所示。国内外学者基于模型试验或有限元数值分析,针对平面空圆管节点(K、N、Y节点等)和空间圆管节点(K–K节点等)给出了热点应力集中系数计算公式[5–7]。
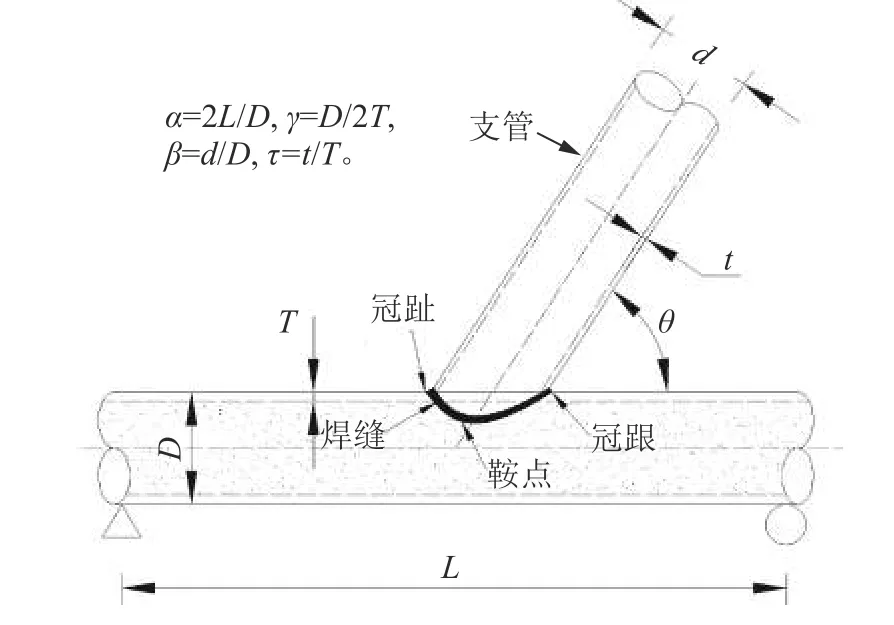
图1 节点无量纲几何参数Fig. 1 Dimensionless geometric parameters
与空钢管节点相比,主管填充混凝土的钢管混凝土节点的HSCF研究还不够充分。Musa等[8–10]对钢管混凝土T型及K型节点的热点应力集中系数进行了试验研究;童乐为[11]、陈娟[12]、Qian[13]、卫星[14–15]、Zheng[16]、Didier[17]等做了疲劳试验和数值分析,主要也都集中于T、Y型节点,通过改变构造尺寸进行研究,并掌握HSCF分布特点。目前,计算灌浆钢管相贯节点HSCF时,设计规范建议采用主管等效壁厚法,再直接套用空钢管节点HSCF计算公式。已有研究结果表明,钢管混凝土桁架主管填充了混凝土后,节点的局部刚度和整体刚度都发生了变化,HSCF数值整体下降,热点应力极值点出现的位置也会发生改变。因此,按空钢管节点的HSCF计算公式来分析钢管混凝土管节点的HSCF分布有时并不符合实际。
圆钢管壁和内填混凝土界面上存在接触、摩擦及滑移等非线性连接关系,既有有限元分析中较多地忽略这种非线性接触关系;而不同的接触关系会在一定程度上影响管节点的刚度分布,进而影响管节点焊缝附近HSCF分布。准确分析钢管混凝土桁架管节点的HSCF分布对开展疲劳寿命评估具有重要意义。
本文以钢管混凝土桁架Y型管节点为研究对象,分析不同摩擦接触条件下,支管受轴拉作用时管节点主管和支管HSCF的分布情况。通过分析比较HSCF最大值位置,以及数值的变化趋势,讨论变化情况,得出HSCF规律性结果。研究结论可为基于热点应力的钢管混凝土桁架焊接钢管节点的疲劳寿命评估提供参考。
1 钢管混凝土桁架Y节点有限元模型
既有钢管混凝土桁架桥梁统计资料表明,结合安全性和经济性要求,钢管混凝土拱肋主管直径较多地集中在600~1 200 mm。本文有限元分析中,钢管混凝土Y节点的主钢管尺寸选用φ800 mm×20 mm,支管尺寸选用φ480 mm×16 mm。同时,模型几何参数满足《公路钢管混凝土拱桥设计规范》[3]的要求,并考虑焊缝的影响。为准确模拟钢管混凝土节点钢–砼界面的非线性接触关系,利用ANSYS有限元分析软件,选择其Solid45、Mass21、Targe170和Conta173单元建立钢管混凝土Y型节点精细有限元模型,如图2所示。钢管材料选用Q345qD钢材,内填混凝土为C50混凝土,根据设计规范材料参数:钢材弹性模量Es=206 GPa,泊松比υs=0.3;混凝土弹性模量Ec=34.5 GPa,泊松比υc=0.2。

图2 钢管混凝土桁架Y节点有限元模型Fig. 2 FEM of CFST Y–joint
钢管对混凝土的约束是通过在有限元分析中引入钢管壁与混凝土之间的接触关系加以考虑。荷载作用下局部变形导致钢管与混凝土之间发生相互挤压或脱离。在ANSYS中,使用面–面接触来模拟钢管混凝土桁架节点接触关系,钢管凹面作为目标面,混凝土凸面作为接触面,网格划分同一位置节点一一对应。钢管混凝土桁架节点的接触问题主要是法向接触,其接触刚度系数根据以往经验取0.1,侵入距离取10–4。
管节点疲劳破坏状态属于钢管局部裂纹扩展,主管内所填混凝土按弹性工作考虑。模型边界如图3所示,主管两端固结,支管作用轴向力540 kN。主管长度取5 m,大于6倍的外径可以消除端部约束对节点区域应力分布的影响;支管长度2.2 m,大于4倍其外径。主管与支管夹角θ=60°,轴向力利用Mass 21单元建立刚性域施加。

图3 边界及荷载施加示意图Fig. 3 Schematic diagram of boundary constraints and load application
由于计算结果对有限元网格尺寸很敏感,因此热点应力外推区域网格尺寸划分足够小。接触分析与下覆单元厚度有关,主钢管单元和下覆混凝土单元均采用六面体单元且下覆混凝土厚度沿径向大小一致。
2 切向接触分析
与空钢管节点相比,钢管混凝土桁架管节点内混凝土对钢管起到支撑作用,增强了节点的刚度。钢管与内填混凝土在界面上存在法向接触关系和切向摩擦关系。基于有限元分析结果,按照ⅡW推荐的公式,采用表面二次外推法进行焊趾处热点应力σhs的计算:
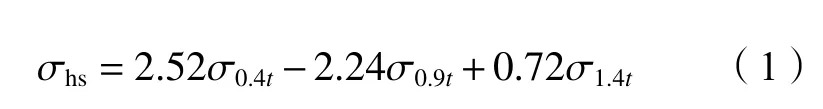
式中, σ0.4t、σ0.9t、σ1.4t分别为距焊趾0.4t、0.9t和1.4t处的应力,t为壁厚。
HSCF可定义为热点应力与名义应力的比值。计算名义应力时,虽然主管、支管相贯连接,但通常仍以支管的圆环面积作为承载面积。
在ANSYS中,可通过接触单元来模拟钢管与内填混凝土之间的切向摩擦关系,而钢管与内填混凝土之间的摩擦系数取值是模拟的关键。不同锈蚀程度的钢板与混凝土之间摩擦系数如表1所示。为研究钢管与内填混凝土界面摩擦系数对节点HSCF分布的影响,本文设计了CFST–0、CFST–35、CFST–60 3个不同摩擦系数(0、0.35、0.60)的有限元数值模型进行分析。
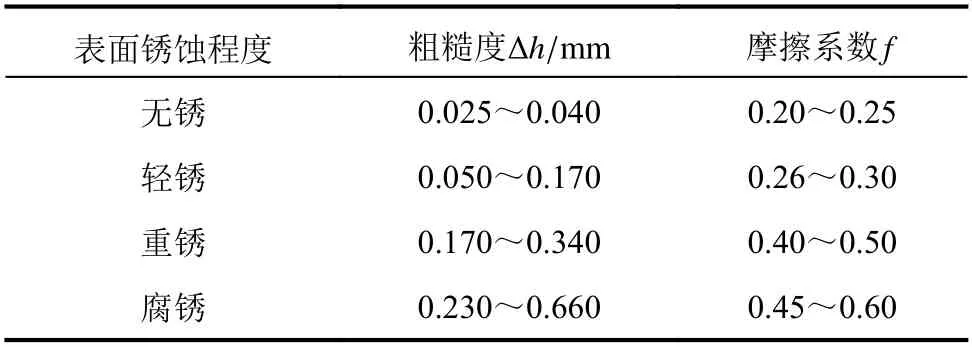
表1 钢板表面粗糙度和摩擦系数关系Tab. 1 Relationship between surface roughness and friction coefficient of steel plate
钢管混凝土桁架Y节点在支管轴力作用下,相贯线焊缝处存在拉应力及剪应力共同作用,为了解切向接触不同摩擦系数情况下,相贯线焊缝焊趾处拉应力分布特征,根据有限元分析结果,以正应力为研究对象,按照式(1)计算得到不同摩擦系数条件下的HSCF。根据对称性仅取焊缝长度范围一半来考虑,沿焊缝冠跟—鞍点—冠趾的焊趾处均匀选取13个点:点1为冠跟,点7为鞍点,点2~6依次为冠跟到鞍点之间的等分点,点13为冠趾,点8~12依次为鞍点到冠趾的等分点,如图4所示。
图5为相贯线焊缝主管和支管13个取值点处热点应力集中系数分布。
由图5可以看出:主管焊趾处HSCF在2.5~5.0之间,沿冠跟—鞍点—冠趾总体趋势在增大,在冠跟处出现最小值2.7,在鞍点和冠趾之间的中点出现最大值4.8;鞍点处的HSCF约为3.9,冠趾处约为4.4。与主管相比,支管HSCF总体较小,分布在1.8~3.4之间;冠跟处HSCF出现最小值1.9,鞍点和冠趾之间出现最大值3.2,鞍点处为2.7,冠趾处为2.1,冠趾处与冠跟处的HSCF相差不大。

图4 应力分析结果提取点布置Fig. 4 Layout of extraction points for stress analysis
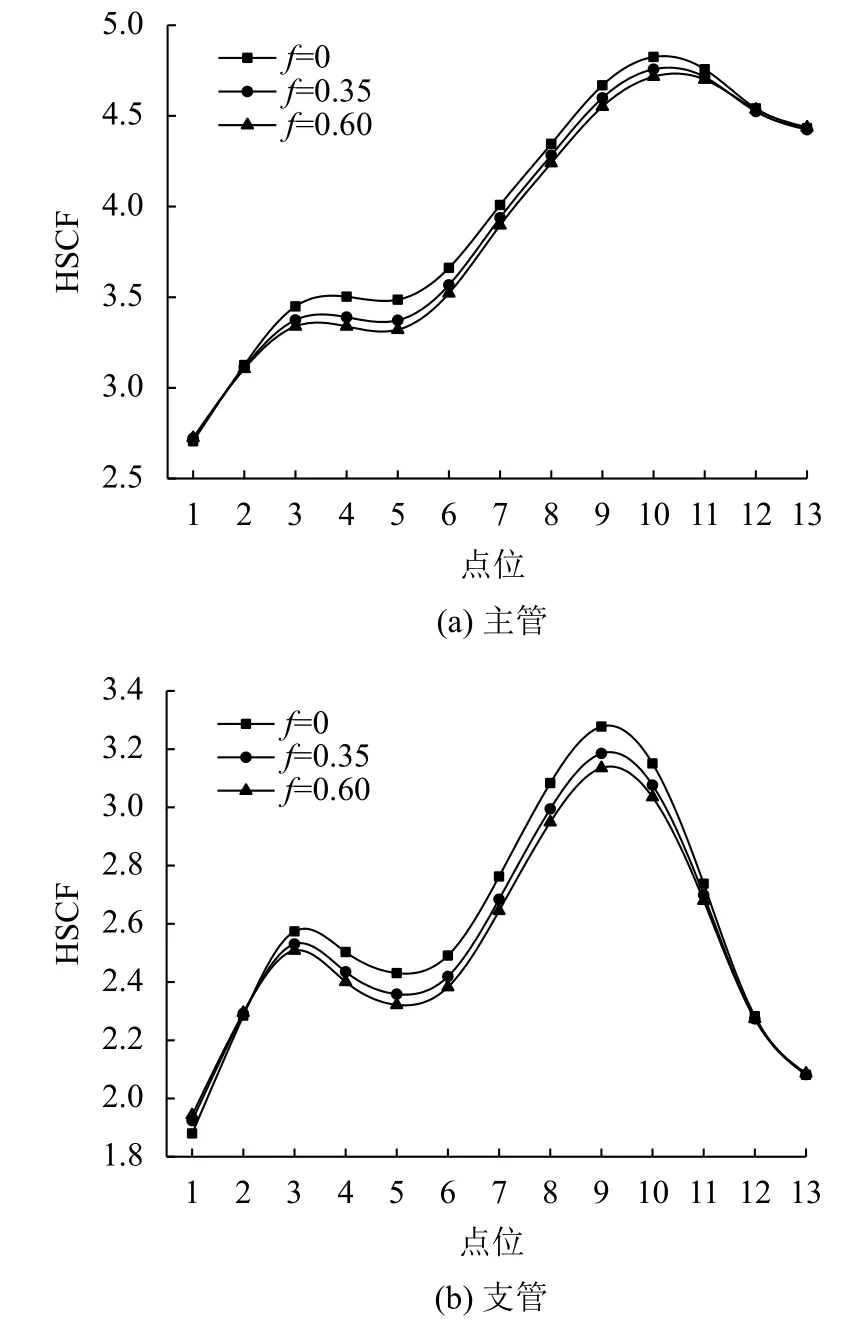
图5 热点应力HSCFFig. 5 hot-spot HSCF
计算结果表明,摩擦系数对热点应力HSCF分布有一定的影响。随着摩擦系数的增大,冠点处HSCF保持不变,焊趾其他位置HSCF有小幅度减小。在支管轴向拉力作用下,主管弯曲变形和径向收缩变形,致使钢管与混凝土之间相互挤压和相对错位,不同的摩擦系数产生不同的界面切向相互作用效应,而冠点位置钢–砼相互脱开,所以摩擦系数对其热点应力集中系数没有影响。
3 法向接触关系分析
利用ASNYS进行钢管混凝土桁架管节点法向接触分析,摩擦系数取0.35;在接触非线性分析中通过不断迭代最终达到收敛条件,确定最终法向接触状态。
图6为钢管混凝土桁架Y节点最终接触间隙图。图6中,0为钢–砼界面发生侵入或接触,负值为钢–砼界面间存在间隙。图7为钢管混凝土桁架Y节点最终侵入深度。图7中,0为界面发生接触或间隙,正值为界面间发生侵入。

图6 接触间隙Fig. 6 Contact gap

图7 侵入深度Fig. 7 Penetration depth
由图6、7可以看出:支管轴向拉力作用下,相贯焊缝位置钢管与混凝土间隙最大,最大间隙0.146 mm;相比上下两鞍点连线横剖面,冠跟与冠趾连线方向纵剖面脱开间隙更宽,脱开区域更大;最大侵入深度出现在鞍点与冠趾中间某个位置,且靠近焊缝附近,主要是由于支管轴向受拉引起主管沿环向受拉,主管在环向拉应力作用下开始沿径向变形,但变形受到内填混凝土的支撑反作用,钢管、混凝土相互挤压作用引起目标面向接触面侵入;最大侵入深度0.001 04 mm,该侵入深度不会影响结构分析结果。
图8为鞍点处横剖面和冠跟与冠趾连线纵剖面处钢管与混凝土间隙分布。节点横剖面径向变形及节点纵剖面竖向变形可以直观反映焊缝位置附近钢管、混凝土相互脱开。
图9为主管钢管和混凝土接触状态。图10为主管钢管与混凝土接触总滑动量。接触状态云图和接触总滑动云图相互印证。滑动量最大区域位于鞍点和冠趾中间焊缝附近,该位置同时是热点应力集中系数最大的区域。图11为主管钢管和混凝土法向接触应力,图12为主管钢管与混凝土切向摩擦应力。
由图11、12可知,法向接触应力最大值为2.14 MPa,切向摩擦力最大为0.75 MPa,最大值位置分布一致。结合图9和10说明,支管轴向拉力作用下,最终状态主管相贯焊缝附近钢管和混凝土相互脱空,冠点附近比鞍点附近脱空区域大,鞍点脱空区域外围即是钢管和混凝土接触挤压最剧烈区域,接触法向压力最大,混凝土对钢管支撑作用最明显。
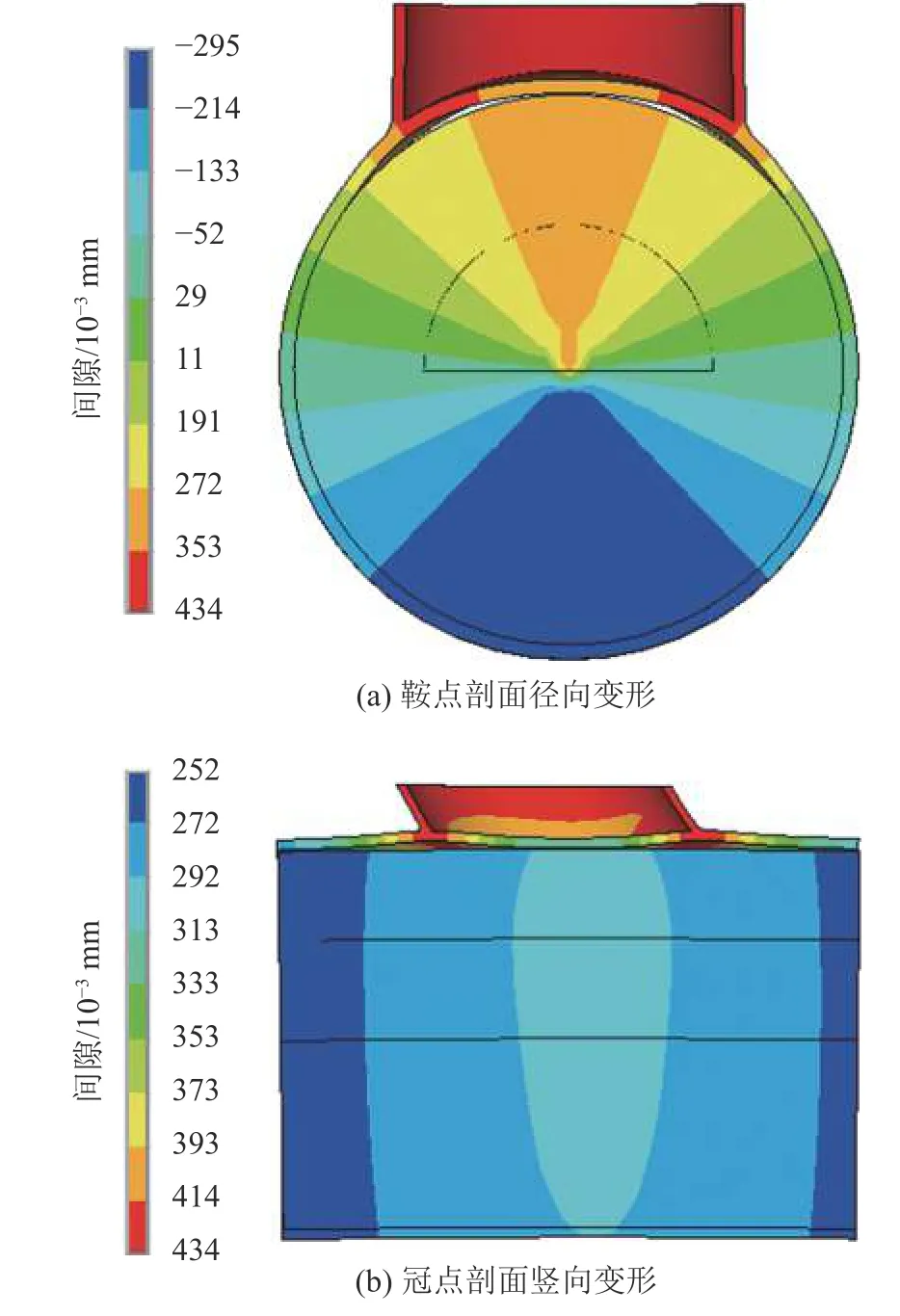
图8 剖面变形Fig. 8 Gap in profile

图9 接触状态Fig. 9 Contact state
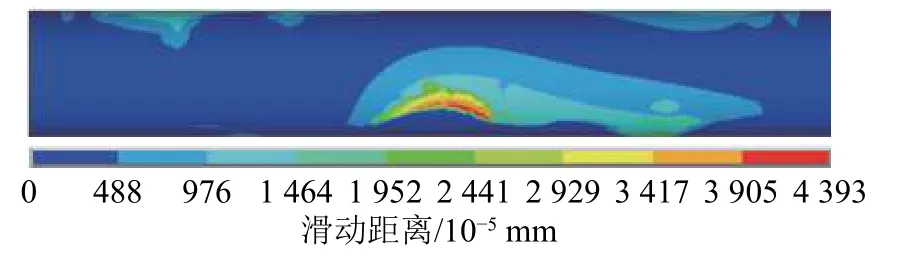
图10 接触总滑动Fig. 10 Total contact slip

图11 法向接触应力Fig. 11 Normal contact stress

图12 切向摩擦力Fig. 12 Tangential friction
4 结 论
1)利用有限元分析方法,考虑钢管与内填混凝土间的非线性接触关系,计算分析得出钢管混凝土桁架的热点应力集中系数可用于指导钢管混凝土桁架焊接管节点基于热点应力方法的疲劳设计。
2)有限元分析结果表明,主管焊趾处HSCF在冠跟处出现最小值,在鞍点和冠趾之间的中点出现最大值;与主管相比,支管HSCF总体较小,冠跟处出现最小值,鞍点和冠趾之间出现最大值,冠趾处与冠跟处HSCF相差不大。
3)钢管与内填混凝土间径向接触分析表明,摩擦系数取值对节点热点应力集中系数分布趋势影响很小,对鞍点和冠趾之间最大值有一定影响。
4)钢管与内填混凝土间法向接触分析表明,轴向拉力作用下节点焊缝附近钢、混凝土相互脱开,冠点附近比鞍点附近脱空区域大,鞍点脱空区域外围是钢管和混凝土接触挤压最剧烈区域,接触法向压力最大,混凝土对钢管支撑作用最明显。
