变量影响值与集群分析相结合的中红外波长选择方法

张 峰， 汤晓君*， 仝昂鑫， 王 斌， 汤春瑞， 王 杰

1. 西安交通大学电力设备电气绝缘国家重点实验室， 陕西 西安 710049 2. 中煤科工集团重庆设计研究院(集团)有限公司， 重庆 400042

引 言

红外光谱分析技术由于其响应速度快、 分析成分多、 灵敏度高、 无损检测等优点， 广泛应用于食品质量检测、 电力设备故障诊断、 石油化工、 煤矿灾害预警等领域[1-4]。 随着光谱仪分辨率的逐步提高， 每个样本获得的谱线多达几千条。 这些谱线无可避免的会包括无用变量甚至是干扰变量。 通常， 当分析物为单组分物质时， 选择主吸收峰位置处的单个谱线利用线性或者非线性拟合方法就能得到满意的结果， 但是当分析物为混合物时， 尤其是混合物之间的吸收光谱重叠严重时， 随机选择几个变量不仅会增加对其他组分的交叉灵敏度， 甚至会降低本身组分的预测精度。 因此， 光谱变量特征选择对于降低模型运行时间， 提高模型的预测精度及降低对其他组分的交叉灵敏度具有重要意义[5-8]。

偏最小二乘法(partial least squares, PLS)具有运行时间短与优化的参数少等特点， 广泛应用于线性分析模型中[10]。 在PLS模型中， 回归系数β是一个重要参数， 基于该参数， 演变了多种变量选择方法， 如蒙特卡洛无信息变量消除法(Monte Carlo non-information variable elimination， MCUVE)[10]、 稳定性竞争自适应重加权采样法(stability competitive adaptive reweighted sampling, SCARS)[11-12]、 变量子集迭代优化(iteratively variable subset optimization, IVSO)[13]。 其中MCUVE与SCARS方法类似， 均是通过蒙特卡洛方法产生大量的样本空间， 获取变量的稳定性， 根据稳定性的值来进行变量筛选， 不同的是， SCARS利用了指数衰减函数来逐步对变量进行剔除， 而MCUVE则是通过阈值来控制变量的选择个数， 阈值的设定采用遍历方法来进行优化选择。 然而， 这两种方法均未考虑到变量之间的相互影响， 当变量之间的共线性较高时， 两种方法选择的变量效果并不好。 IVSO算法利用蒙特卡洛方法在变量空间中生成大量的子集， 对变量空间分别建立PLS模型， 对每个模型中的回归系数进行归一化处理， 随后将这些模型的回归系数进行求和并归一化来得到新的权重值。 利用加权二进制采样技术根据权重值的大小来分配在下次迭代中变量被选择的概率， 这样回归系数值较大的变量更有机会在下次迭代中被选择。 然而回归系数会随着样本的不同而变化， 这样导致了IVSO算法选择的变量随机性大。

针对上述变量选择方法存在的问题， 提出了一种基于变量影响值与集群分析相结合(impact of variable and population analysis, IVPA)的变量选择方法。 为了评价提出方法的性能， 将该方法应用于烷烃类气体的中红外数据集中， 并与SCARS和IVSO方法的预测结果进行了对比。 结果表明， IVPA方法对异丁烷的预测最准确， 对其他组分的交叉灵敏度最低， 能够对光谱交叠严重的组分进行变量选择。

1 IVPA算法基本原理

1.1 样本空间中变量影响值

将扫描获得的光谱数据用矩阵Xn×p表示，n为样本的个数，p为谱线数量。yn×m为n个样本所对应的分析物浓度信息。 当分析物为单组分时，m取值为1。 当分析物为多组分时，m大于1， 此时可以用PLS2模型或者利用PLS1模型经过m次循环来建立模型。 采用PLS1建立红外光谱定量分析模型可以表示如式(1)

y=Xβ+e

(1)

式(1)中，β为回归系数向量， 表示为β=[β1,β2,…,βp]T，y为分析第i种组分时的浓度向量， 其中i≤m，e为随机误差向量。 将其中一个变量在其值的基础上乘以小于1的系数α1， 得到新的变量V1， 然后乘以大于1的系数α2， 得到变量V2， 对获取的新的变量分别建立PLS模型， 得到对应的交互验证均方根误差UEi与DEi。 该过程循环p次， 这样每个样变量的影响值可以由式(2)计算

IVi=UEi-DEi

(2)

1.2 IVPA变量选择方法

IVPA算法融合了变量的影响值与变量空间中最优模型出现的频率两个重要指标。 在每次迭代过程中， 同时计算变量的影响值与频率， 根据变量影响值采用加权自举采样技术将变量划分为精英变量与普通变量， 在普通变量中剔除频率较低的变量， 这样保证了每次迭代中剔除了变量影响值较低与最优模型中出现的频率较低的变量。 当迭代达到设定的次数时， 算法结束。 IVPA算法详细步骤如下：

Step1： 迭代开始， 初始变量个数为p。 依据式(2)， 计算每个变量的影响值IVi， 根据IVi的值采用加权自举采样技术将变量划分为精英变量与普通变量。 此时， 精英变量的个数约为p的0.632倍[14]；

Step2： 根据集群分析理念， 采用蒙特卡洛算法从p个变量中随机选择p1个变量， 生成W个变量空间，p1值的可以选择为变量个数的0.2倍， 降低变量之间的共线性带来的影响。 对W个变量空间建立PLS模型， 获取每个模型的交叉均方根误差(root mean squared error of cross validation, RMSECV)值， 将W个RMSECV值从小到大进行排序， 选择预测结果较好的βW个模型， 根据式(3)计算每个变量出现的频率fi

(3)

式(3)中，Fij为变量i是否出现在预测结果较好的第j个模型中， 若出现， 则为1， 否则为0，β为比例系数， 取值小于0.5。

Step3： 利用指数衰减函数确定每次迭代时保留的变量数目， 指数衰减函数可以表示如式(4)

ri=ae-ki

(4)

式(4)中，ri为第i迭代后剩余的变量数， 其中a=(p/2)(1/(N-1)),k=ln(p/2)/(N-1)，i为当前的迭代次数，N为设置的总迭代次数，p为上次迭代保留的变量数量。 通过剩余变量数可以计算出每次迭代中需要剔除的变量。 当普通变量的数目大于剔除的变量数时， 剔除普通变量中频率低的变量； 当普通变量数目小于剔除的变量时， 剔除全部的普通变量， 并且从精英变量中剔除平均影响值低的变量；

Step4： 记录每次迭代过程中变量空间中W个模型的最小均方根误差(root mean squared error, RMSE)， 同时更新变量数p的值，p=ri；

Step5： 若迭代次数小于设定值时， 返回step1， 否则， 执行Step6；

Step6： 选择最小的RMSE所对应的变量子集作为最优变量组合。

2 实验部分

2.1 光谱数据的获取

实验所采用的傅里叶变换红外光谱仪型号为Spectrum Two， 其气体池长度为10 cm， 扫描范围400～4 000 cm-1, 波数分辨率为1 cm-1， 扫描类型为吸光度。 为了降低随机噪声的干扰， 每个样品扫描次数设置为8。 待分析物的目标气体为甲烷(CH4)、 乙烷(C2H6)、 丙烷(C3H8)、 异丁烷(i-C4H10)、 正丁烷(n-C4H10)共5种烷烃类气体。 实验时， 采用标气进行光谱扫描， 五种气体的浓度范围分别为0.01%， 0.02%， 0.05%， 0.1%， 0.2%和0.5%。 五种组分气体在0.05%下的吸光度光谱如图1所示。

图1 五种气体在浓度为0.05%时的吸光度光谱

从图1中可以看出， 5种气体在3 000 cm-1附近吸收峰最高， 为烷烃类气体的主吸收峰， 在1 200～1 700 cm-1范围内， 为烷烃类气体的次吸收峰。 可以看出， 无论是在主吸收峰还是在次吸收峰， 5种气体之间的光谱交叠严重。 从图中还可以看出， 5种气体的光谱发生不同程度的基线漂移， 根据前期研究成果[15]， 采用一种惩罚最小二乘方法对光谱数据进行了基线校正。

2.2 IVPA参数确定

IVPA算法中需要优化的参数有： (1)算法的迭代次数N； (2)样本空间中变量乘以小于1的系数α1； (3)样本空间中变量乘以大于1的系数α2； (4)变量空间中子模型的个数W； (5)变量空间中预测效果较好的模型占全部模型W的比例系数β。 可以按照以下步骤来进行最优参数选取。

(1)系数α1与α2的优化。 固定算法中其他参数的值，N设置为50，W设置为1 000，β设置为0.1。 同时α1在0.1到1之间以间隔为0.1变化，α2在1.1到3.1之间以间隔为0.2变化， 共经历99次IVPA运算后， 获得99个RMSE值， 选择RMSE最小的值对应的α1与α1作为最终优化的值。 RMSE值随α1与α2变化趋势如图2所示。 从图2中可以看出， 当α1取值为0.7，α2为1.9时， 获得的RMSE值最小。

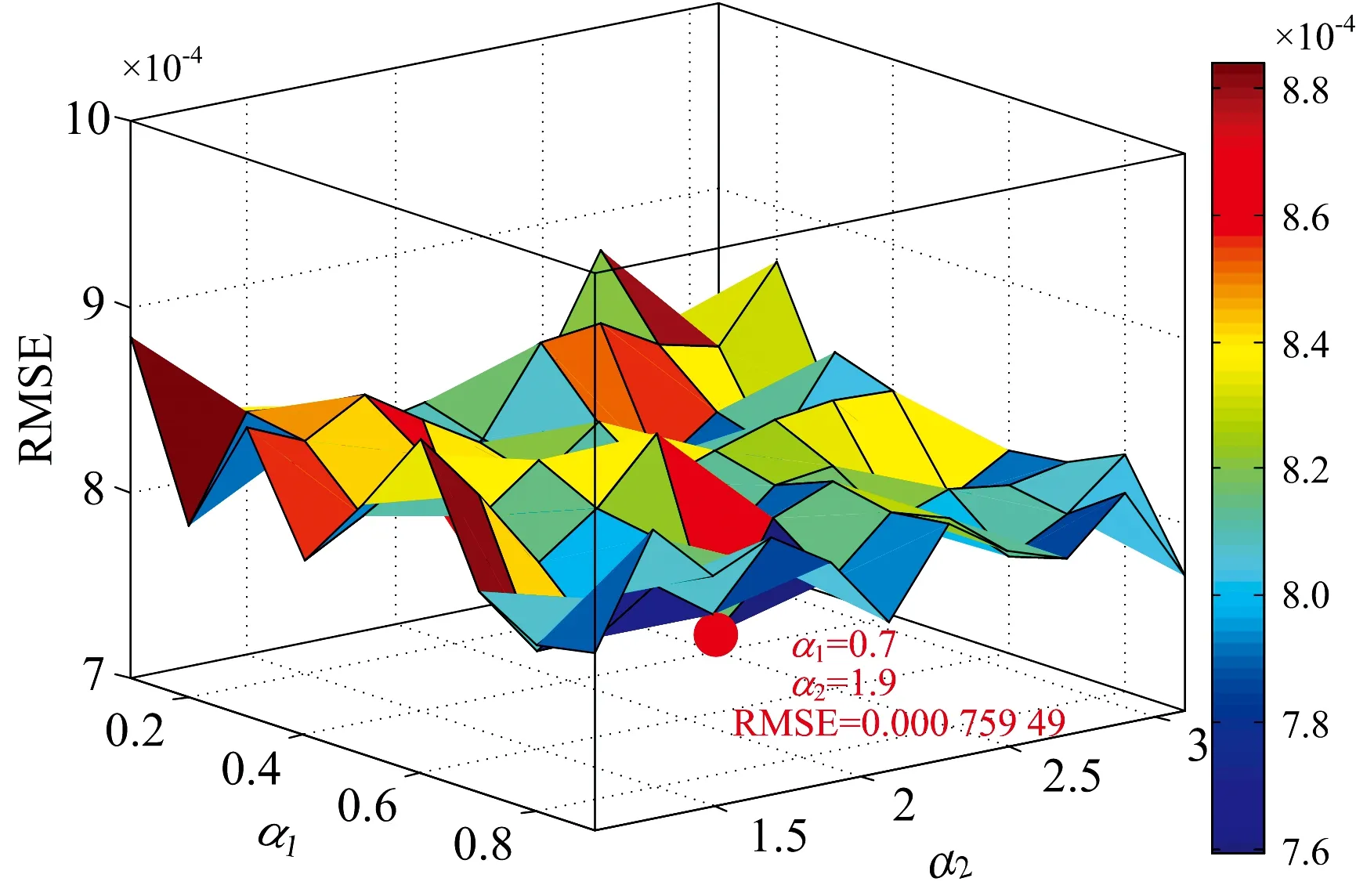
图2 IVPA算法中参数α1与α2的优化选择

(2)迭代次数N的选取。 将第一步获得的最优α1与α2值作为IVPA作为常量， 同样，W设置为1 000，β设置为0.1。N的取值为20到160， 间隔为20，N每次取值时， IVPA算法循环执行30次。 经历240次IVPA循环后， 获得8组N取不同值时的RMSE值， 每组RMSE个数为30个。 图3为RMSE随N的变化趋势。 可知， 当N为80时， RMSE获得的均值最低， 并且上下波动幅度不大。

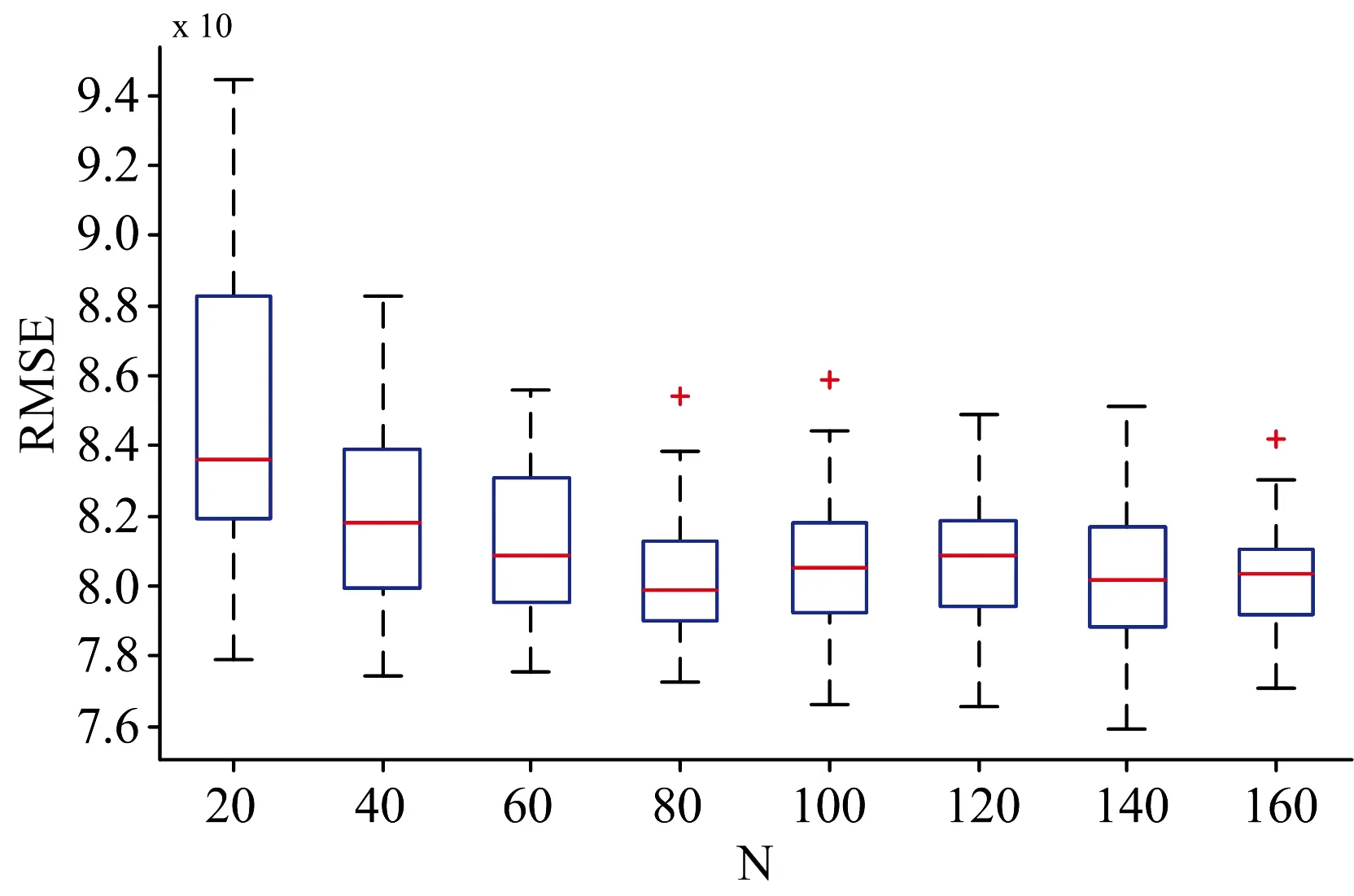
图3 IVPA算法中参数N的优化选择

(3)变量空间中子模型个数W与比例系数β的确定。 通常W的值设置较大， 保证了每个变量都会分配到对应的子模型中， 体现了集群分析中群体的理念。β通常设置为0.05到0.3之间， 为集群分析中最优选择的概念。 将前2步选择的α1，α2与N作为已知参数，β的取值范围为0.05～0.3之间， 间隔为0.05，W以间隔500在1 000到5 000之间取值。 这样， 经过60次计算后， 以RMSE最小值所对应的W与β作为最终选择的参数。 图4为RMSE随W与β的变化趋势图。 由图可知， 当W为3 500，β等于0.05时， RMSE最小。 因此， 最终获得的参数为： 算法迭代次数N为80、 系数α1为0.7， 系数α2为1.9， 子模型个数W为3 500， 预测效果较好的模型占全部模型比例系数为0.05。

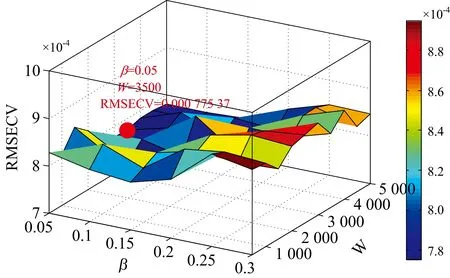
图4 IVPA算法中参数W与β的优化选择

3 结果与讨论

为了评价算法的性能， 以光谱交叠最严重的异丁烷光谱为例， SCARS， IVSO及IVPA 3种变量选择方法进行变量选择， 选择的变量如图5所示。

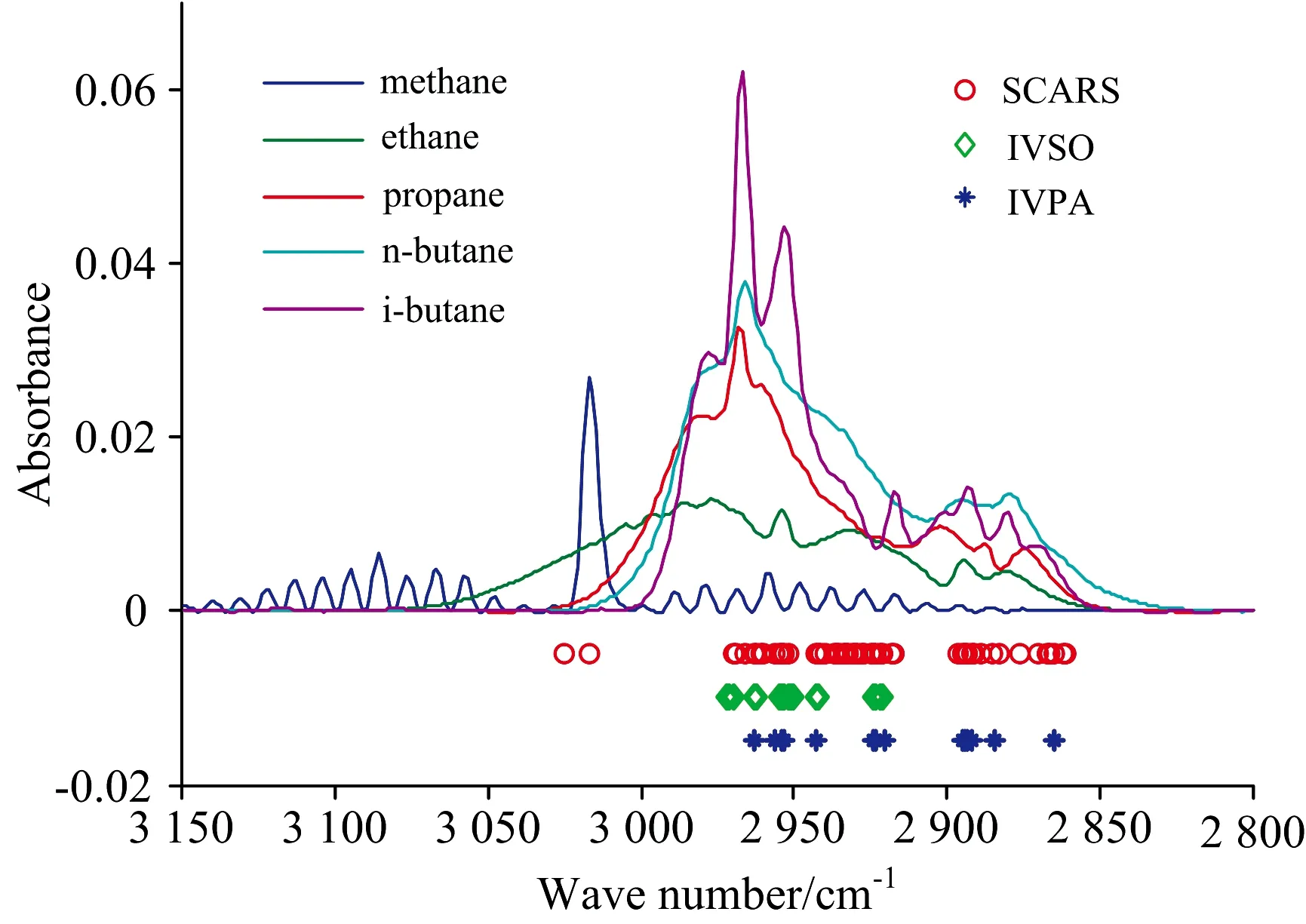
图5 三种方法选择的变量分布图

从图5中可以看出， SCARS选择的变量最多， 并且分布比较散， 除此之外， 还选择了无吸收峰范围内的变量， 这些变量被认为是干扰变量与无用变量； IVSO选择的变量次之， 集中在2 950 cm-1附近； IVPA选择的变量最少， 选择的变量覆盖了异丁烷的吸收峰的主要区域。

将浓度为0.05%的五种烷烃气体的光谱作为输入变量， 根据以上述3种变量选择方法建立的模型对五种气体浓度进行预测， 其预测结果如表1所示。 从表中可以看出3种方法对正丁烷的交叉灵敏度最高， 这是因为正丁烷与异丁烷的分子结构近似， 其吸收光谱形状接近； 对甲烷的交叉灵敏度较低， 这是由于甲烷在大于3 000 cm-1范围的吸光度较低， 3种方法选择的变量集中在大于3 000 cm-1范围内。 还可以看出IVPA对异丁烷的预测结果最准确， 最大交叉灵敏度为1.02%， 最小交叉灵敏度为0.11%。 SCARS与IVSO对异丁烷预测的结果相当， 除此之外， IVPA对其他4种气体的交叉灵敏度最低， 表明所提出的方法能够有效的对光谱交叠严重的变量进行提取， 并能很好的对其进行分析。

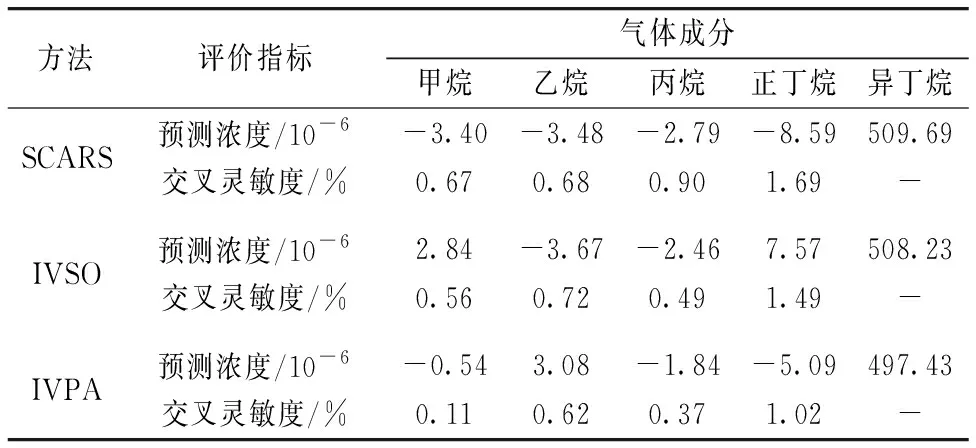
表1 三种方法对500 ppm烷烃气体的预测结果

4 结 论

利用傅里叶变换红外光谱仪对烷烃类气体进行定量分析时， 分析物的种类多且光谱交叠严重， 严重制约着定量分析结果的准确性及运算效率。 提出了一种基于变量影响值与集群分析的变量选择方法， 将该方法与SCARS、 IVSO三种变量选择方法来对烷烃类5种气体进行了变量提取， 以异丁烷为例， 对其进行了预测， 并分析了对甲烷、 乙烷、 丙烷、 正丁烷的交叉灵敏度。 结果表明， IVPA方法对异丁烷的预测结果最好， 对其他气体的交叉灵敏度最低， 能够对交叠严重的光谱进行变量提取， 具有实际的应用价值。