冲击荷载下红砂岩非线性黏弹性损伤本构研究*

赵 涛 王 磊 苏宏明 陈世官 秦 越

(西安科技大学建筑与土木工程学院， 西安 710054， 中国)

0 引 言

我国西部白垩系地层多为富水砂岩，因其成岩相对较晚而表现出胶结弱、强度低、孔隙率大等力学性质(王渭明等， 2011； Wang et al.，2017； 孙利辉等， 2019)。人工冻结工程和寒区基础设施建设过程中，爆破应力波对此类岩石造成的损伤破坏(伍法权， 2011； 闫长斌， 2017； 谢小帅等， 2019)，可利用室内SHPB冲击试验进行模拟研究，而建立合适的动态本构模型，是研究此类岩石动力学特性的关键，也为工程实际中的边坡、节理岩体、地基等在动力荷载下的稳定性分析提供参考与依据(兰恒星等， 2019； 周家文等， 2019)。

目前，有关岩石类材料动态本构关系的研究已取得了较多的成果，赵光明等(2013)、谢理想等(2013a，2013b)根据软岩及混凝土材料在动载下的应力-应变曲线特点，采用损伤体代替朱王唐模型中的弹性元件，建立了一种损伤型黏弹性动态本构模型方程； 付玉凯等(2013)、解北京等(2019)运用弹塑性理论，结合煤、岩本构的研究成果和层叠模型原理，并充分考虑了组合煤岩体在动态破坏过程中的应变率相关性和损伤特性，构建了7参数组合煤岩层叠本构模型； 翟越等(2011)针对岩石类材料的动态力学特性，基于损伤演化和元件模型理论，建立考虑损伤的黏弹塑性动态本构模型，并推导出本构方程的微分表达式； 刘红岩等(2014)采用考虑岩石细观损伤的非线性元件、节理面闭合及剪切变形元件等3个基本元件的串联来模拟静态应力分量，采用黏性元件来模拟动态应力分量，建立了贯通节理岩体动态单轴压缩损伤本构模型； 王恩元等(2019)基于岩石力学强度理论和统计损伤理论，建立了冲击载荷下三轴煤体动态损伤本构模型，该模型综合考虑了轴向静载、围压和冲击载荷等因素，明确地反映了3种因素对煤体动力学特征的影响； 周永强等(2017)在弹性模量上考虑了刚度的率效应和在D-P准则上考虑了强度的率效应，进而提出了考虑率效应的岩石材料次加载面动态本构模型； 王春等(2017)基于连续因子、应变等效原理及统计损伤理论定义岩石的损伤变量并推演损伤演化方程，采用组合模型法建立岩石的本构模型； 蔡灿等(2015)提出Maxwell体、Bingham体和损伤体的并联模型，借助拉普拉斯变换，引入基于岩石孔隙、裂隙劣化的损伤变量，导出了中低应变率下的岩石动态损伤本构模型； 李夕兵等(2019)、宫凤强等(2013)建立了基于Weibull分布的动态统计损伤模型，对花岗岩在循环冲击荷载下的力学关系进行表征，并对其损伤演化过程进行了研究。可以看出，以上对于岩石类材料的本构模型研究大都是根据相应材料的力学性质，运用不同的强度准则、损伤演化以及元件组合等方法进行分析得到的，并在相应的材料中得到了很好的验证，这对本文建立常温及冻结红砂岩在冲击荷载下的本构模型具有一定的指导作用。

根据红砂岩的动力学特征，提出以非线性体、Maxwell体和基于Weibull分布的损伤体并联的黏弹性本构模型，对其进行了试验验证，并和以Lemaitre等效应变假设建立的损伤本构方程进行对比，对两者的优缺点和适用性进行了比较与讨论，并对其参数敏感性进行分析，为涉及此类岩石的西部地质工程在受到冲击荷载下的动力响应分析提供理论依据。

1 朱王唐本构模型

朱王唐非线性黏弹性本构模型能够较好地描述固体材料在黏弹性变形范围内的力学性能，因而被广泛地应用在研究混凝土、有机玻璃、岩石等材料在应变率10-4s-1～103s-1范围内的力学性能。该模型由1个非线性弹簧体和2个Maxwell体组成(图1)。

图1 朱王唐模型

其本构方程为：

(1)

模型中的非线性弹簧用来描述平衡态应力状况， 2个不同的Maxwell体分别描述不同应变率条件下的黏弹响应，其中低频部分的φ1在10～102s-1之间响应，高频部分的φ2在10-4～10-6s-1之间响应。

2 基于Weibull分布的损伤本构模型

为准确表达红砂岩动力学本构关系，现对朱王唐本构模型各部分元件进行如下改进：(1)将方程中表示应变率无关的平衡态应力的多项式部分继续保留，即为非线弹性弹簧； (2)根据文献内容(Ma， 2017)，在冲击荷载作用下的时间尺度是以1～102μs计量的，因而低频Maxwell体没有足够的时间松弛，这里看成是弹性模量为E1的简单弹簧； (3)红砂岩为非均质类材料，其内容存在着大量的裂隙、孔隙和孔洞，当岩石受力产生形变即发生损伤，故对此模型增加损伤体D。据此可得改进后的本构模型如图2所示。

图2 改进后的本构模型

由图2可知，改进后的本构模型由非线性体、Maxwell体和损伤体并联组成，其应力关系为：

σ=σ1+σ2+σ3

(2)

其中：(i)非线性体的本构关系为：

σ1(t)=EΔε(t)+χε2(t)+κε3(t)

(3)

式中：EΔ=E0+E1。

(ii) Maxwell体元件为弹性元件和阻尼元件串联而成，其应力-应变关系为：

σ2(t)=σ21(t)=σ22(t)

(4)

ε2(t)=ε21(t)+ε22(t)

(5)

σ21=E2ε21(t)

(6)

(7)

对式(5)进行求导，联立式(4)、式(6)及式(7)得：

(8)

对式(8)进行Laplace变换后得：

(9)

(10)

其中：σ(0)=0，代入式(10)整理得：

(11)

对式(11)进行Laplace逆变换得：

(12)

(13)

(14)

(iii)现对模型中的损伤体作以下假设： 1)岩石内部连续且损伤均匀化，即原始缺陷均匀化； 2)岩石冲击过程视为在恒应变率加载条件下完成的； 3)各微元体强度服从Weibull分布，其概率密度为：

(15)

式中：m和α为分布参数，大小与材料的性质和形状有关。

试件损伤程度与各微元所包含缺陷的多少有关，损伤变量D是对材料损伤程度的度量，其与微元破坏的概率密度关系为：

(16)

积分后得：

(17)

由式(17)可得损伤体本构关系为：

(18)

因此，由式(2)可知红砂岩基于Weibull损伤分布的动态本构方程为：

(19)

3 基于Lemaitre等效应变本构方程

根据红砂岩在冲击荷载下应力-应变曲线明显的分段性，这里对朱王唐本构模型进行改进。首先，冲击荷载下低频Maxwell体没有足够的时间来松弛，因而用简单弹簧代替。简化后的本构模型如图3所示，简化后的模型本构关系为：

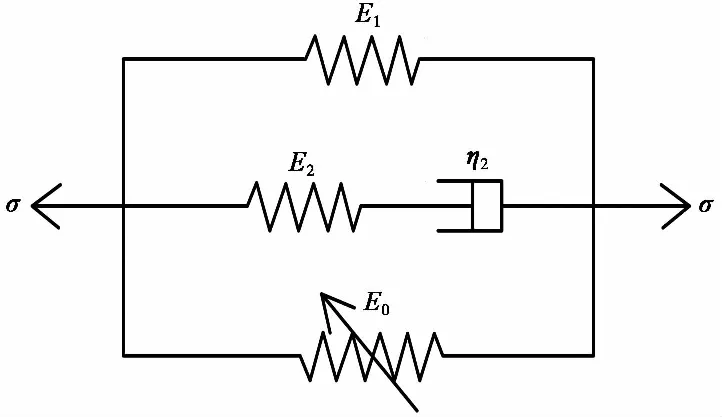
图3 简化后的本构模型

(20)

其次，对模型作如下假设：(1)红砂岩存在应变阈值，当应变大于一定值时，试件出现损伤； (2)岩石内部微裂纹数量与变形量、应变率成正比； (3)将材料损伤演化过程看作为一个促进的热激活过程。

根据Lemaitre应变等效原理，考虑损伤的岩石本构关系为：

σ=(1-D)Eε

(21)

当D=0时，材料无损伤； 当D=1时，表示材料完全丧失承载能力，将式(19)代入，则：

(22)

这里将D用式(21)呈现的率型损伤演化规律来表示：

(23)

则对(22)积分后得：

(24)

将式(23)代入式(21)可得出红砂岩动态损伤本构方程：

(25)

4 试验验证与参数分析

4.1 试验曲线拟合与验证

为验证上述新建本构关系的适用性，利用分离式Hopkinson压杆装置对不同温度的(20 ℃、0 ℃、- 10 ℃)饱和红砂岩试样进行不同应变率下的冲击试验，并获取相应的动态应力-应变曲线。

冲击荷载作用下反应岩石类材料性质的应力-应变曲线可分为峰前部分和峰后部分，因此对上述两种本构方程分别进行峰前应力曲线和整个应力-应变曲线的拟合验证。

首先对基于Weibull分布的非线性黏弹性本构方程进行验证，式(19)中共8个未知参数，首先根据20 ℃红砂岩准动态应力-应变曲线拟合得到EΔ、E2、χ和κ，然后对高应变率下冲击试验的应力-应变曲线拟合，确定ED、η2、α和m。对20 ℃饱和红砂岩在不同应变率下的应力-应变关系拟合结果见图4。

图4 基于Weibull分布本构方程20 ℃试验验证

根据试验所得， 20 ℃、0 ℃、-10 ℃红砂岩的阈值应变ε0分别为0.0018、0.0026和0.0045。对基于Lemaitre等效应变假设建立的损伤本构方程的试验验证时，式(24)中共9个未知参数，首先根据试件无损伤时的准动态应力-应变曲线确定E0、χ、κ、E1和E2，再对高应变率冲击曲线进行拟合确定其他参数。对20 ℃红砂岩在不同应变率冲击荷载作用下的应力-应变关系拟合结果见图5。

图5 基于Lemaitre等效应变假设损伤本构方程20 ℃试验验证

结合图4和图5可以看出，(1)本构方程对红砂岩在冲击荷载下的峰前应力部分的拟合中，基于Weibull分布的本构方程和基于Lemaitre等效应变假设的本构方程的拟合曲线和试验数据都保持着良好的一致性，拟合精度R2>0.97，但后者的拟合精度更高，R2>0.99； 从曲线形态上看，虽然前者的拟合精度略低于后者，但前者拟合曲线的塑性发展阶段能更好地反映出实际的应力-应变关系，即应变硬化和塑性流动等特征，而后者虽拟合精度高，但其拟合曲线的塑性发展阶段近似为直线，这与这类孔隙率大的非均质软岩材料在冲击荷载下的非线性特征是不相符的。(2)对整个应力-应变曲线的拟合中，基于Weibull分布的本构方程对试验数据的拟合度较高，R2>0.96，而基于Lemaitre等效应变假设的本构方程的拟合精度较低，R2<0.9，其误差大于岩土工程力学计算中5%的误差范围要求，因此不能作为红砂岩动态力学性能的表征； 从曲线的形态上看，前者的拟合曲线表现出明显的分段特征，能准确地反映出红砂岩在冲击荷载下的线弹性阶段、塑性发展阶段和应变软化阶段，可对红砂岩动力学特性进行准确表征，但后者的拟合曲线只与红砂岩应力曲线的峰后部分有较高的吻合度，无法反映峰前应力变化的非线性特征，本构方程拟合精度达不到规范要求而不适用于对此类红砂岩动态全应力曲线的表征。

综上所述，基于Weibull分布的本构方程更适合对红砂岩在冲击荷载下的峰前应力曲线和整个应力-应变曲线关系进行表征，而基于Lemaitre等效应变假设的本构方程只适合对此类砂岩的峰前应力曲线部分进行表征，无法对其动态全应力曲线的峰前部分进行准确表征。

现利用试验所得0 ℃和- 10 ℃红砂岩动态应力-应变关系对本文新建本构方程进行适用性验证，如图6～图10所示。

图10 基于Weibull分布本构方程各参数的影响性分析

图6 基于Weibull分布本构方程0 ℃试验验证

从图7a、图7b、图8a、图8b中可以看出，基于Weibull分布本构方程的拟合曲线与试验数据吻合度高，整体上对峰前应力的拟合精度高于整个应力曲线的拟合，但拟合精度R2均大于0.95，可以准确地反映- 10 ℃红砂岩在冲击荷载下的力学本构关系，这说明基于Weibull分布的非线性黏弹性本构方程适用于对常温以及人工冻结下白垩系红砂岩的动力响应解答，具有一定的实际推广价值。

图8 基于Weibull分布本构方程- 10 ℃试验验证

从图7a、图7b、图9a、图9b可以看出，基于Lemaitre等效应变假设的本构方程对- 10 ℃冻结红砂岩进行拟合验证时，峰前应力部分的拟合曲线与试验数据吻合度高，拟合精度R2>0.96； 而对整个应力部分的拟合验证中，与20 ℃的拟合结果相同，都无法准确表达红砂岩峰前应力变化特征，故认为基于Lemaitre等效应变假设本构方程适用于红砂岩峰前应力解答，对其全应力解答存在一定的局限性。

图7 基于Lemaitre等效应变假设本构方程0 ℃试验验证

图9 基于Lemaitre等效应变假设本构方程- 10 ℃试验验证

4.2 本构模型的参数分析

图11 基于Lemaitre等效应变假设本构方程各参数的影响性分析

从图10可以看出：(1)基于Weibull分布本构方程的5个参数中，峰值应力强度与本构方程各参数呈正相关的为E0、η和ED，呈负相关的为m和α； (2)参数η对本构曲线的形态无影响，本构方程拟合曲线只随η值的改变而整体上下平移； (3)参数E0、ED、α和m对本构方程拟合曲线的塑性发展阶段的斜率以及峰值应力强度产生影响，其中，E0的取值对拟合曲线形态影响较小，对本构曲线的敏感性较低，而α和m取值变化范围很小时便会对本构曲线的形态产生较大的影响，具有较高的敏感性。

从图11中可以看出：(1)基于Lemaitre等效应变本构方程的参数中，E0值的大小与拟合曲线的峰值应力强度呈正相关，参数KD、δ和η2则呈负相关； (2)参数E0、δ和KD对拟合曲线塑性发展阶段的形态有影响，其中，E0对曲线影响范围更广，δ和KD对曲线的敏感性更强； (3)参数η2值的改变对本构曲线的形态无影响，主要是对初始弹性阶段的长短以及峰值应力强度的大小产生影响。

综上所述，在红砂岩本构关系研究中，对峰前应力部分解答时上述两种本构方程均可，对全应力解答时则只能使用基于Weibull分布的非线性黏弹性损伤本构方程，并可根据各参数对本构曲线的影响，确定出精确度较高的参数值，从而更好地指导工程实践。

5 结 论

(1)根据饱和红砂岩在静载以及动载作用下的力学特征，对朱王唐本构模型进行改进，建立了非线性体、Maxwell体和微元强度服从于Weibull分布的损伤体并联的动态本构模型，该模型能很好地对红砂岩在常温和人工冻结状态下的动态本构关系进行表征。

(2)以朱王唐本构模型为基础，对其进行简化，建立了基于Lemaitre等效应变假设的损伤本构方程，该模型能很好地对红砂岩峰前应力部分进行表征，但无法准确反映全应力曲线的峰前应力变化特征，对红砂岩的动力学响应解答存在局限性。

(3)通过对本构方程各参数对拟合曲线的敏感性分析，可以准确地了解各参数对红砂岩本构关系的影响，从而确定出精确度较高的参数值，更好地指导工程实践。