改进型XGBoost算法模型的企业电力负荷电费优化
2021-06-10仲立军杨玉锐周晓琴牛中伟周子誉
仲立军, 杨玉锐, 周晓琴, 牛中伟, 周子誉
(国网嘉兴供电公司,浙江 嘉兴 314000)
0 引 言
在企业工业用电以及用户的用电中,电费的整体架构通常包括基本电费、电度电费和功率因数调整电费等不同的形式。化工企业多数实行24 h连续生产,对供电可靠性要求高,多数采用双电源以保证供电质量[1],因此无法有效通过生产负荷分时段调整,以利用分时电价差降低电度电费。现有技术中的企业功率因数在一定程度上虽然能够满足企业用电的需求,但是无功率太多,电费的优化空间相对比较小[2]。在计算基本电费时,需要根据企业用户的实际用电容量或者最大用电需量进行计算。在众多用电过程中,企业用户难以对未来的用电负荷情况进行判断,使得在选择基本电费计收方式时,难免与自身实际用电负荷存在偏差,容易引起基本电费虚高。这就需要一种方法实现企业电费优化。
1 负荷预测大数据模型设计
本文通过研究浙江某工业园区化工企业用电负荷特征,根据企业月度用电最大需量波动率分组,采用改进型XGBoost算法模型[3],构建化工企业月度用电最大需量精准预测模型。为企业合理选择基本电费计算方式提供指导,帮助企业合理降低用电成本。采用的大数据模型如图1所示,下面分别对不同的算法模型进行说明。

图1 负荷预测大数据模型设计
1.1 改进型XGBoost算法模型
本文采用改进型XGBoost算法模型,在传统XGBoost算法模型的基础上加入逐步回归算法模型[4],具有以下技术优势。
(1) 对大量的负荷数据比较敏感,计算速度比较快,数据效率输出比较高。
(2) 模型构建较为快捷,适用范围广,在电力负荷电费预测和计算过程中表现出较好的适应性。
(3) 克服了现有技术分类算法效率低和分类性差的问题,提高了评估企业电力负荷电费的能力。
本文采用改进型XGBoost算法模型的核心意义在于使用CART模型。首先对负荷预测模型进行定义,设定其输出的目标函数,目标函数由训练损失L(Θ)、正则化Ω(Θ)两种不同的函数表示式构成,数学表达式如式(1)所示。
Obj(Θ)=L(Θ)+Ω(Θ)
(1)
对上述函数求最小化,其本质是对训练损失L(Θ)和正则化Ω(Θ)求最小化。通过图形使拟合曲线达到最佳,最终预测的负荷方差最小[5],输出的结果较为稳定。
评估目标为:将出现的损失函数在拟合曲线图中呈现欠拟合的形态,输出的优化正则化项图形表现为过拟合形态,使最后的输出函数达到最小值。这样就能够使用输出函数的模型实现较佳的评估效果。流程示意图如图2所示。
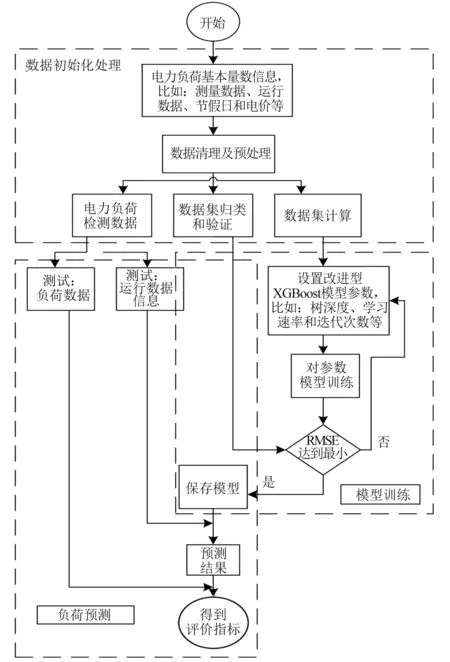
图2 改进型XGBoost模型构建流程示意图
下面分步骤说明上述函数。
(1) 构建多个决策树,反复进行迭代计算,将每个决策树通过设置根节点和叶结点的方式,构建出最佳决策树模型。
(2) 在每次迭代开始之前,计算损失函数在每个训练样本点的一阶导数gi和二阶导数hi。
(3) 采用贪心算法将不同的决策树模型对不同的叶节点和根节点的计算输出的预测值进行评价。
(4) 将每次计算输出的决策树ft(x)通过迭代模型进行计算,迭代模型公式为:
(2)
当出现多个决策树时,为了提高决策树的精度,通过以下函数进行优化:
(3)

(4)
改进型XGBoost算法模型的负荷预测模型可以用以下公式表示。
(5)

通常,在进行负荷评估时,将改进型XGBoost算法模型内的各种决策树模型进行固定设置,令q(x)=K,对Obj(t)进行求导,其输出的一阶导数等于0,决策树上的叶子节点j的参数值可通过以下函数表示。
(6)
式中:Gj为叶子节点j的所有输入样本的一阶导之和;Hj为叶子节点j所有输入样本的二阶导之和;λ为正则化系数。ω为构建出的决策树输出的分数向量。
则对电力负荷电费评估和优化的目标函数为:
(7)
式中:T为构建出的决策树中每个叶的节点数量。
通过该方法,能够将电力负荷运行情况转化为大数据模型的方式表示,提高了数据计算的直观能力。通过不断地调整数据权重能够不断地训练单个弱学习器,有助于纠正和调整弱学习器输出的数据残差,将原始构建出的多个不同决策树学习器进行加权求和,最终输出较为准确的预测数值。
为了进一步提高上述计算精度,本文采用逐步回归算法模型对上述算法进一步修正,以提高评估精度。
1.2 逐步回归算法模型
对逐步回归算法模型的构建方法进行说明,假设存在n个不同的企业基本电费类型。企业基本电费类型中的种类为m,每种m个数据类型中的数据量为p,反映用户实际用电情况的矩阵为An×p,用户理论用电矩阵为Cn×m,评估误差矩阵为En×m,则引出关系式为:
Cn×m=An×pPp×m+En×m
(8)
(9)
在对个别企业基本电费进行数据分析时,可以令m=1,此时,式(10)可以转化为:
(10)
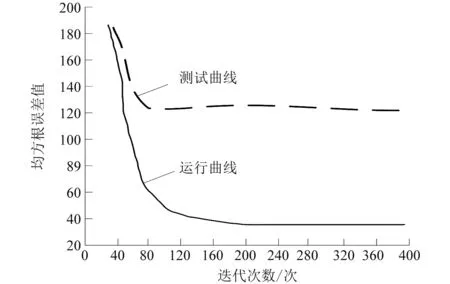
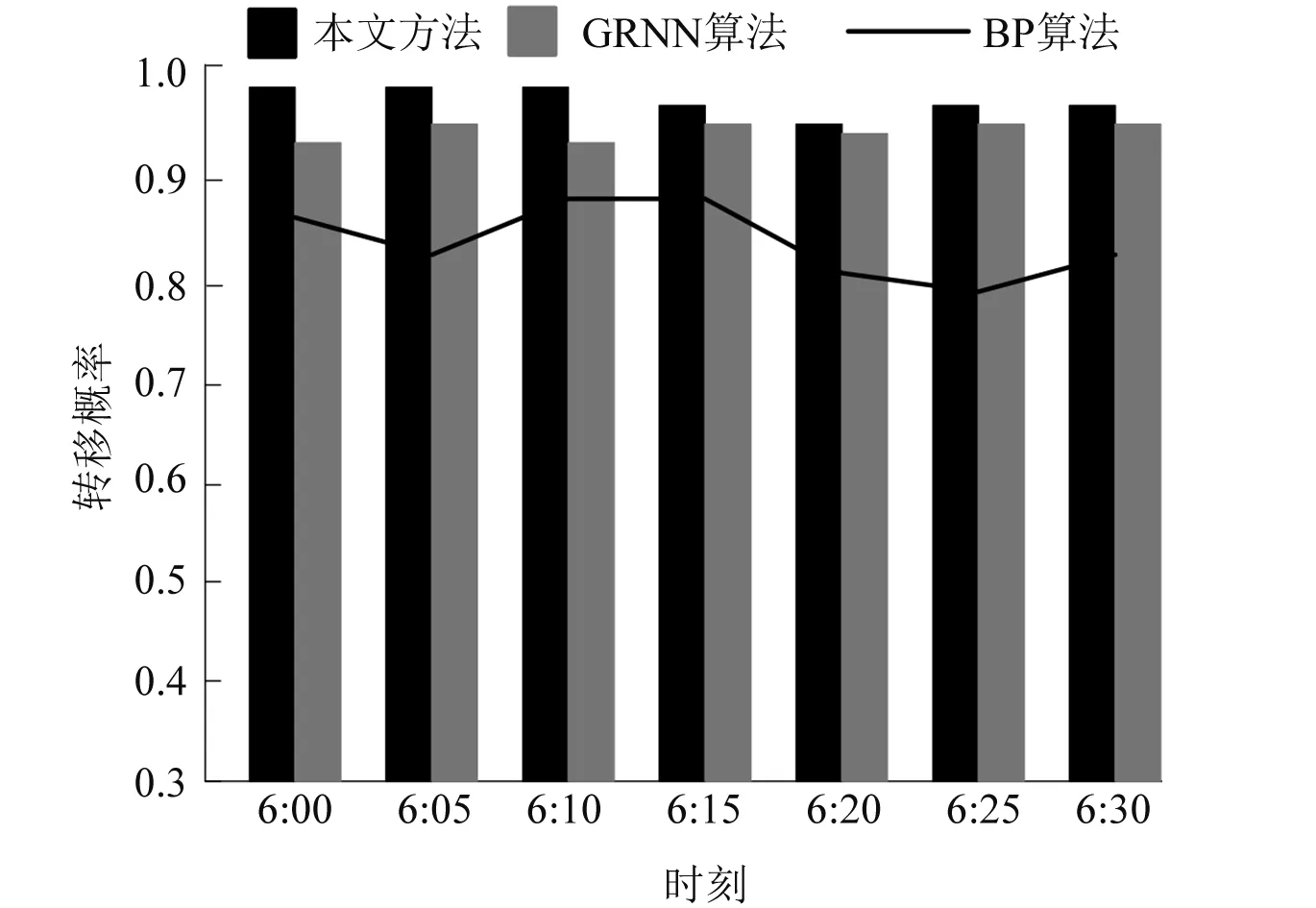
式中:aki为企业基本电费的变量数据之间是相关系数为1的线性相关量。当r(ATA) 通过上述模型的构建,逐步回归算法模型内的总离差平方和与上述回归方差平方和关系可以用以下关系式表示。 S总(t)=S回(t)+S残(t) (11) S回(t)=S总(t)-S残(t) (12) 其中: (13) 当在企业基本电费的数据信息中剔除一个数据ai,则函数中的S回(t)转变为S回(t-1),再通过公式Δi(t)=S回(t)-S回(t-1)表示异常的数据信息ai对分类属性c的总方差贡献值。然后调取数据统计量: (14) 本文主要验证改进型XGBoost算法模型的工作效率。仿真试验时,工作环境为Python3.5。该算法模型的参数为:每个决策树的树深度取6,学习效率为0.43,进行400次迭代计算[10]。决策树剪枝后的数值为0.3,决策树每个叶子输出的权重值为6,其中对决策树进行随机采样输出的数值比例为0.7。改进型XGBoost算法模型的正则化被命名为L2, 将本文的改进型XGBoost算法模型与BP、GRNN算法分别进行对比验证。 本文实例数据为浙江某工业园区内化工企业2015年1月至2018年8月最大需量及影响因素指标数据。以需量变异系数0.08为阈值,变异系数>0.08为波动较大组,变异系数≤0.08为波动较小组。园区两组类型企业2018年8月需量数据如表1所示。 表1 样本1园区部分企业2018年8月最大需量数据 通过设置如表1所示的数据信息,进行数据分析。 本文以园区企业2015年1月至2017年12月的需量及其相关影响指标数据作通过数据采集和设置,首先需要对获取的数据信息进行预处理,归一化处理函数为: 为训练集,进行模型训练;以2018年1月至8月的数据为验证集,对模型效果进行评价。样本数据表如表2所示。 表2 样本2 试验数据表 (15) 在进行精确度评价时,采用均方根误差(root mean square error,RMSE)和平均绝对误差百分比(mean absolute percent error,MAPE),其中均方根RMSE误差数据模型为: (16) 平均绝对误差百分比MAPE模型可以为: (17) 通过对改进型XGBoost算法模型进行参数设置,在具体应用时,需要调用XGBoost函数库中的CV函数进行数据信息计算,通过400次的迭代计算,输出如图3所示的误差曲线示意图。 通过图3可以看到,在经历一段时间的运行后,为了避免模型在运行过程中出现过拟合现象,将改进型XGBoost算法模型的迭代次数取值230。 图3 负荷预测均方根误差曲线示意图 下面以几种简单的影响因素作为示例性分析,如图4所示。 通过图4可以看到,负荷影响因素不同,则均方根值不同,各个影响因素的分布比例都不相同。进而可以直观地看出不同因素的影响。 图4 改进型XGBoost算法模型中不同影响因素的特征重量级分布图 将BP、GRNN算法分别与本文的改进型XGBoost算法模型进行对比分析,得出如图5所示的对比示意图。 分析图5可知,改进型XGBoost算法模型预测准确度较高,且较为稳定,更适用于电力超短期负荷预测。 图5 不同方法的预测准确性分析对比示意图 本文根据当前电力负荷预测的需要,提出了新型的负荷预测模型,应用了改进型XGBoost算法模型,通过调整权值的方式实现弱分类器和学习器的训练和学习,提高了数据输出的精确度。通过试验,本文方法能够直观地看出负荷影响因素,误差低,能为企业电力负荷的预测做出一定的贡献,但是尚且存在其他不足,需要进行进一步的研究。

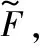
2 案例分析及验证


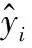

3 结束语
