基于复阻尼模型水平剪切型结构的时域解析算法

焦浩鑫,丁肇伟,陈龙珠

(1.上海市公共建筑和基础设施数字化运维重点实验室,上海 200240;2.上海交通大学船建学院土木系,上海 200240)

0 引言

目前,在结构动力分析中,可用黏性阻尼模型和复阻尼模型等来反映振动能量的耗散。黏性阻尼模型在数学上具有求解和计算简便的优点,在工程实际中得到了广泛的应用[1]。但由黏性阻尼模型求出的结构动力响应可知,其能量耗散与所受外部动荷载或地基基础运动激励的频率有关。而已有试验结果证明,在较大的频率范围内,结构系统的能量耗散与激励频率基本无关[2]。采用复阻尼模型进行分析时,结构在振动一周内的能量耗散受外加激励频率的影响甚是轻微,符合能量耗散与激励频率无关的试验现象。因此,从能量耗散的角度来看,采用复阻尼模型进行结构动力分析,会更为准确。

定性来说,采用数值方法计算结构动力响应时程曲线,具有很广的适用范围。但由于时域运动方程中含有不稳定的子集,采用逐步积分法计算时,会出现发散现象[3]。时域数值计算方法的稳定性受损耗因子、激励持续时间以及时间积分步长等因素的影响。张辉东等[4]指出,复阻尼模型下时域数值解法的发散程度,随着结构损耗因子的增大而增大。潘玉华等[5]在对含复阻尼运动方程的求解稳定性进行研究时发现,其与结构的自振周期、地震荷载持续时间以及复阻尼模型参数的大小有关,即当荷载持续时间与结构自振周期的比值大于临界值时,采用时域数值方法对复阻尼下的动力响应进行求解,会引起计算结果的发散。张辉东等[6]对Rayleigh阻尼模型和复阻尼模型下的地震时程响应进行的对比分析表明,后者计算得到的结构动力响应大于传统的Rayleigh阻尼模型计算得到的结果,而且其稳定性和精度与时间积分步长有关。

综上所述,对可体现能量耗散与激励频率无关的复阻尼模型,摸索保证所求出的结构动力响应结果稳定收敛的计算方法,具有较为重要的学术和应用价值。朱镜清等[7]通过忽略计算结果中的发散项来保证动力响应的稳定性,但这种方法缺乏理论根据[8]。周正华等[9]提出了一种可进行时域计算的复阻尼本构方程,使得计算结果稳定收敛。REGGIO等[10]将Maxwell-Wiechert本构模型应用于复阻尼模型中,得到了计算结果稳定的运动方程,但模型参数的确定对应用带来了不便。孙攀旭等[11]将复阻尼运动方程等效为频率相关的黏性阻尼运动方程,既保证了能量耗散与激励频率无关,又避免了复阻尼时域计算结果的发散。孙攀旭等[12]提出了滞变阻尼模型的时域理论和数值计算方法,确保了结构时域计算结果的稳定收敛。虽然上述计算方法能够保证时域动力响应的收敛稳定,但计算过程比较繁杂,而且计算精度与效率尚有待于提高。另外,以上均为数值计算方法,不能解析表达出结构动力特性以及响应随结构参数的变化规律。

针对上述存在的问题,本文以较为常见的多层水平剪切型结构为研究对象,参照三对角Toeplitz矩阵的递推方法[13],推导出它的各阶自振频率、振型函数的解析形式。在此基础上,由Fourier变换推导出复阻尼下结构动力响应的频域解析解,然后由其反变换得出结构在地震作用下各层位移的时程解析解,便于直观地观察结构动力特性以及响应随结构参数的变化规律。文中将通过算例,对本文方法和数值方法的计算结果进行比较分析。

1 结构动力特性的解析算式

首先列出结构在地震作用下的运动方程。如图1所示的水平剪切型结构,取各自由度相对地面的位移作为运动变量,在地震作用下有运动方程:

图1 多自由度模型计算简图Fig.1 Model for structures with multi-degree of freedom

(1)

为分析结构的动力特性,假设结构体系的第一层质量为mb,水平层间刚度为kb,其余各层的质量和刚度分别为m、k,其自由振动方程为:

(2)

式中结构动力特性矩阵[A]为:

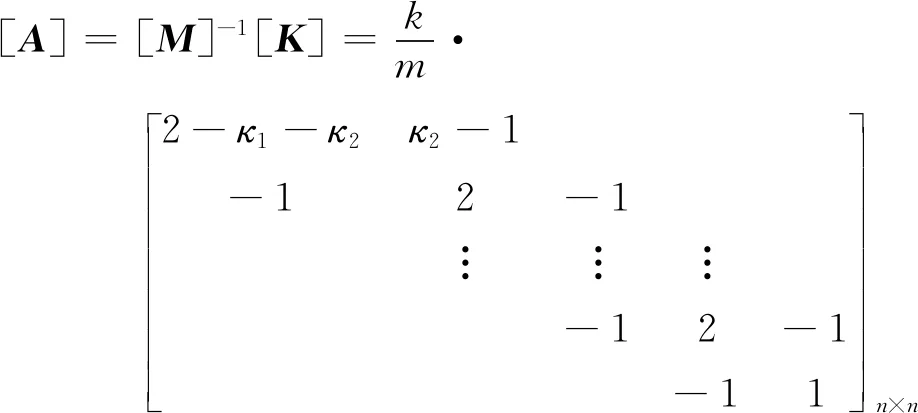
(3)

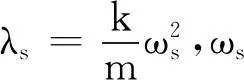
可见,各阶自振圆频率ωs为矩阵[A]的特征值,对应的各阶振型{φs}为矩阵[A]的特征向量。

三对角矩阵[A],已不是经典三对角Toeplitz矩阵。借鉴于文献[13]中求解三对角Toeplitz矩阵特征值和特征向量的数学方法,可以得到如下线性递推式(j=1,2,…,n)和边界条件:

(4)

式(4)第一行线性递推式的解有如下形式:

(5)

式中:βs1、βs2均为常系数;rs1、rs2则为特征方程r2-(2-λs)r+1=0的两个根,满足韦达定理:

rs1+rs2=2-λs,rs1rs2=1

(6)

将式(5)代入式(4)第2行边界条件中,可得:

(7)

要使式(7)有非零解,其系数行列式必为零,即:

(8)

(9)

式中:θs为第s阶自振周期对应的变量,由下式求出:

(10)

由式(5)可得各阶振型为:

(11)

式(11)表明,对于图1所示的多自由度结构,其每阶振型均是以j为自变量的简谐函数。

2 结构动力响应的时域解

2.1 复阻尼结构传递函数的解析算式

为得到复阻尼结构的传递函数,首先对无阻尼下的式(1)进行Fourier变换,有:

(12)

(13)

利用振型的正交性和矩阵对角化方法,得:

(14)

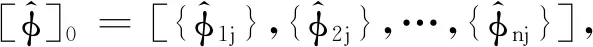
(15)

为对复阻尼下的结构进行动力响应分析,本文借鉴文献[14]中采用的复刚度法。考虑各层损耗因子为不同值时,也可使用本文方法进行计算,但本文为简便公式推导,取各层损耗因子为相同值η,分别用k(1+iη)、kb(1+iη)代替式(3)中k、kb,则复阻尼下结构的传递函数可表示为:

(16)

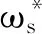
(17)

2.2 复阻尼结构动力响应的时域算法

在地震时程数据的处理中,快速Fourier变换(FFT)具有重要作用。快速Fourier变换后给出的频域数据所包含的信息与原始时域数据完全相同,仅仅在信息的表示方法上有所不同。通过对频域信号进行逆变换后,可以方便地得到其时域信号。为此,对地面运动加速度时程信号进行快速Fourier变换:

(18)

式中:N为采样点数;Δt为采样间隔;Δω为快速Fourier变换的频率分辨率。

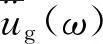
(19)

另外,在Fourier变换中,对具有N个数据的离散采样点,其离散Fourier变换同样具有N个数值,而在频域分析中通常只采用前N/2+1个。为通过逆变换得到具有同样采样频率的结构动力响应,需在传递函数Hj(iω)中按Fourier变换的数值排列方式补齐后部分数据。

3 算例比较分析

为检验本文方法的正确性,用MATLAB编制相关计算程序,并将计算结果与文献[12]采用希尔伯特变换的数值方法所得时域计算结果进行对比。

3.1 单自由度地震响应计算

根据美国国家地震信息中心网站(NEIC)及中国地震台网(CENC)获取的地震时程数据,选取Ⅷ度El-centro波、Kobe波和唐山波进行时程分析。El-centro波、Kobe波的记录信号为地面水平向加速度在50 s内的采样数据,其采样间隔为0.02 s,唐山波的记录信号为地面水平向加速度在20 s内的采样数据,其采样间隔为0.01 s。根据文献[15]中相关规定,取加速度最大值为0.2g,设计分组为第一组。对于各个地震记录,依据所取基本烈度对应的地面加速度峰值进行处理,处理后输入的地震加速度时程如图2,其中Kobe波的持续振动时间比El-centro波的明显要短。根据频谱分析,Kobe波、唐山波和El-centro波的主要成分分别低于5 Hz和8 Hz。

图2 输入地震波加速度时程Fig.2 Acceleration time-history curves of input seismic waves

该算例假设结构的质量为1×106kg,自振频率为0.96 Hz,复阻尼结构损耗因子为0.1,初始时刻结构处于静止状态,分别采用文献[12]数值算法和本文给出的解析方法计算求得结构的位移动力响应,结果如图3和表1。由图可知,两种方法的计算结果基本一致,时程曲线吻合较好。由表1可知,两种方法计算得到的位移响应峰值,相对误差在3%以内,初步检验了本文方法在计算单自由度体系位移响应的正确性。计算过程还表明,在单自由度体系分析时,本文方法克服了求解复阻尼动力响应的发散问题,计算结果不但稳定收敛快,而且精度相对也好,计算效率相对更高。

表1 两种方法的单自由度位移响应幅值对比Table 1 Comparison between displacement response amplitudes of the SDOF system with two methods

图3 两种方法的单自由度位移响应时程Fig.3 Displacement responses of the SDOF system with two methods

3.2 多自由度地震作用下的动力响应

采用文献[16]给出的7层框架结构进行分析,每层的等效质量为1.239×106kg,水平剪切刚度等效为1.615×106kN/m(即κ1=κ2=0),结构的黏性阻尼比ξ=0.05。对复阻尼的结构损耗因子与黏性阻尼比的近似关系,由文献[17]可知,当η=2ξω/ωs时,采用黏性阻尼与复阻尼计算得出的单自由度系统动力响应完全相同。考虑到影响结构地震响应的频率成分主要集中在第一阶共振频率ω≈ωs区域内,本文采用η=2ξ=0.10进行计算分析。

计算得该7层框架结构体系的第1和第7阶自振频率分别为1.20 Hz、11.24 Hz,假设结构在初始时刻为静止状态,分别用本文和文献[12]两种方法计算该结构体系的地震位移响应,结果如图4和表2。

图4 两种方法的多自由度顶点位移响应时程Fig.4 Vertex displacement responses of the MDOF system with two methods

表2 两种方法的多自由度顶点位移响应幅值对比Table 2 Comparison between vertex displacement response amplitudes of the MDOF system with two methods

图4是结构顶层位移响应的时程曲线,可知,两种方法得到的计算结果基本一致,计算过程稳定收敛。表2所列两种方法计算得到的结构顶点位移峰值也较为接近,其相对误差在5%以内。

通过对比表1和表2可知,在进行多自由度结构的位移响应计算时,其计算结果的相对误差明显大于单自由度结构体系。其原因可能是多自由度结构体系中的阻尼更加复杂,若仅考虑整体结构的黏性阻尼比ξ=0.05,则会导致黏性阻尼模型的计算结果存在相对更大的误差。

3.3 结构动力响应幅值随底层刚度的变化

为观察两种方法求得结构位移、加速度峰值随底层刚度而变化的规律,本节采用第3.2节中结构质量、层间刚度以及复阻尼结构损耗因子的取值,但在一定范围内改变刚度比kb/k∈(0,2]进行计算,结果如图5、图6所示。

图5 顶点位移幅值随刚度比的变化规律Fig.5 Variation of vertex displacement amplitude with the stiffness ratio

图6 顶点加速度幅值随刚度比的变化规律Fig.6 Variation of vertex acceleration amplitude with the stiffness ratio

图5给出了所得结构顶点位移峰值随刚度比的变化曲线。由图可知,从整体上看,随着底层刚度的不断变化,两种方法计算得到的结构顶层位移峰值相互比较接近(本文解析方法得到的位移峰值稍大)。由图还可看出,随着底层刚度的变化,数值方法得出的位移峰值计算曲线存在一定程度的离散波动现象,而本文方法计算的曲线相对光滑得多。

图6给出的是结构顶层加速度峰值随底层刚度比而变化的曲线。为了便于观察两种方法计算曲线间的差别,该图的竖轴采用了对数坐标。由图可见,本文方法的曲线仍然光滑稳定,但数值方法所得曲线的离散波动现象比图5的更为显著,这对计算结构的层间内力峰值来说,容易产生较大的误差。

4 结论

本文通过理论推导以及算例分析,得到以下3点主要结论:

(1) 借鉴三对角Toeplitz矩阵特征值问题求解的递推方法,得到了多层水平剪切型结构的自振频率和振型函数的解析算式;在此基础上,提出了计算复阻尼模型下由地面运动引起的结构响应时程曲线的解析算法。

(2) 对单层和多层复阻尼结构,采用本文解析算法和文献数值方法,分别计算了由地面地震运动引起的结构位移响应,结果表明两种方法得到的位移响应时程曲线接近,其位移峰值的相对误差均在5%以内。

(3) 采用本文方法和文献数值方法求解多层结构加速度峰值随底层刚度的变化,本文方法的计算曲线光滑,避免了数值方法计算曲线上较为强烈的离散误差问题。

本文主要探讨算法的有效性,而结构其他参数对地震响应的影响,有待于进一步分析研究。