运行状态下海上单桩风机系统自振频率分析
2021-06-09王丕光刘晶波
王丕光,刘晶波,赵 密
(1.清华大学 土木系,北京 100084;2.北京工业大学 建筑工程学院,北京 100124)
0 引言
近年来,随着传统能源的日益匮乏和环境条件的不断恶化,可再生能源的开发与利用已成为各国研究发展的重点,而海上风能作为绿色可再生能源是现在的研究热点之一。与陆上风能相比,海上风能具有风速高、有效发电时间长和不占用陆地资源等优势[1]。我国海岸线漫长,具有丰富的海上风电资源,一批海上风电场已经建成或正在建设中[2]。
单桩基础结构形式简单,受力明确,设计及施工方便,在国内外已建成的海上风电场中所占比例达70%[3]。大直径单桩基础为开口钢管桩,刚度大、抗弯性能好,主要适用于水深小于25 m的海域;直径通常为4~6 m,埋深一般为20~40 m,长径比(嵌固深度与外径比)一般不超过8,属于刚性短桩[4]。近年来,国内外学者对海上风电单桩基础的水平承载特性[5-9]和风、波浪和地震作用下海上单桩风机结构的动力响应[10-17]进行了广泛的研究。
海上风机设计时应考虑荷载激励频率与结构自振频率的关系,保证系统自振频率避开荷载激励频率。目前国内外多采用柔-刚设计模式进行风机系统的结构与基础设计[1],即系统基频在1P(发电机的转动频率)和3P(叶片的扫掠频率)之间。目前,国内外学者对海上风机系统的频率进行相关的研究[18-24]。Bhattacharya和Adhikari[18]以及Andersen等[19]将风机基础简化为水平和旋转两自由度的弹簧,建立了风机系统的自振频率求解方程。Prendergast等[21]研究了冲刷对海上风机系统自振频率的影响。Arany等[23]将风机基础简化为三弹簧模型,即水平、旋转和耦合弹簧,并提出了海上风机系统自振频率的解析模型。阳春宝等[25]建立了近海单桩基础风机系统自振频率求解数值计算方法,并进行了系统频率偏移因素分析。
海上风机在运营期间会承受上风、浪的荷载,风浪荷载会引起风机系统的水平侧移;随着水平侧移的增大,风机基础的刚度会降低,从而导致系统频率的偏移;风机系统基频降低过大可能会造成风机系统频率与风机运行荷载频率接近,从而造成风机结构反应过大。因此很有必要讨论桩基水平侧移对风机系统自振频率的影响。已有的研究表明[17,26],相比于浪、荷载和塔筒风荷载,风机运行状态下产生的风荷载对风机体系动力反应的贡献占大多数。本文基于有限元软件ABAQUS平台,建立了沙土中单桩式海上风机结构系统的自振频率分析模型,并讨论了运行状态下风机基础水平侧移对大直径海上单桩式风机系统自振频率的影响。
1 单桩式海上风机数值模型
单桩式海上风机结构的分析模型如图1所列。本文将塔筒和单桩离散为弹性梁柱单元,风机叶片、吊篮和轮毂简化为塔顶的集中质量,整个模型在有限元软件ABAQUS中实现。以下将详细介绍变截面塔筒的简化模型、桩-水相互作用模型和桩-土相互作用模型。
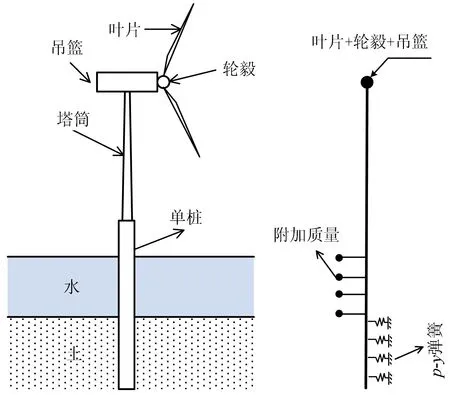
图1 单桩式海上风机结构Fig.1 A monopile offshore wind turbine system
1.1 塔筒简化模型
基于分段思想,将塔筒简化分为相互连接的若干段的组合,当段数足够多时,每一段都看作为等截面梁。为竖向一致截面的柱体。第i段梁的等效刚度和等效线密度可表示为[27]:
(1)
(2)
式中:E为弹性模量;ρ为密度;A为截面面积;I为截面惯性矩。
1.2 桩-水相互作用
地震作用下,柱体与周围水体之间是一个复杂的动力相互作用问题。水体的存在不仅会改变结构的动力特性,还会对结构产生附加动水压力。该动水压力可以等效为结构周围水体的质量与结构加速度的乘积,这些水的质量称为附加质量。空心柱体外域和内域水体的附加质量为[28]:
(3)
(4)
式中:mo和mi分别表示外域和内域水体的单位高度附加质量,a和b分别表示空心圆柱的外半径和内半径,h表示水深,λ=(j-0.5)/h,ρw表示水体的密度,In和Kn分别表示第一类和第二类修正的n阶贝塞尔函数。
1.3 桩-土相互作用
研究桩-土相互作用问题时,一般将地基沿桩深度方向离散为一系列弹簧,而桩被简化为梁柱单元,当土体变形较大时,可以采用p-y曲线理论进行研究。该方法考虑土体的非线性,p和y分别表示土体某深度处土体的反力和桩基的位移,而p-y曲线用来描述两者的关系。目前,p-y曲线方法已经广泛应用于地震工程及近海工程中,并被许多国家或地区的规范所采用。
本文桩-土相互作用采用Reese等[29]提出的沙土p-y曲线。如图2所示,沙土p-y曲线由一段抛物线和三段直线组成。土体极限承载力ps取公式(5)和(6)计算得到的较小值,即
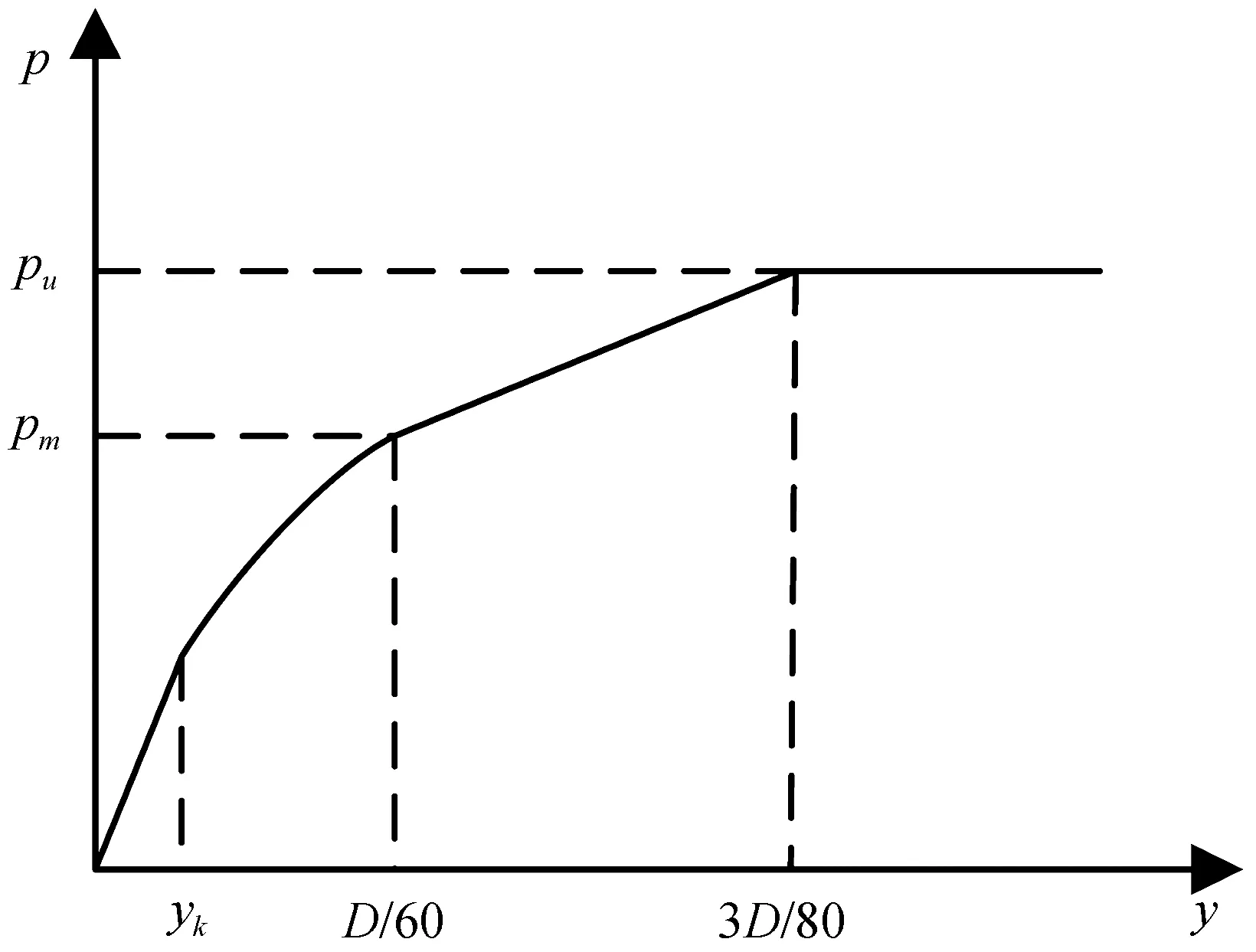
图2 沙土p-y曲线Fig.2 p-y curve of sand
(5)
psd=KaDγ0z(tan8β-1)+KoDγ0ztanφtan4β
(6)
式中:γ0为土体的有效重度,本文中取为10 kN/m3;z为土体深度;D表示桩径;α=φ/2,β=45°+φ/2,Ka=tan2(45°-φ/2),φ为内摩擦角;Ko=0.4。
极限承载力为pu=Asps和y=D/60对应的土体抗力为pm=Bsps,其中As和Bs为深度相关的无量纲系数;初始直线段部分为p=kszy,ks表示初始地基模量系数;抛物线部分为yk=(C/kz)n/n-1,相应的p-y曲线为:
(7)
本文中p-y曲线通过ABAQUS中的非线性弹簧单元实现。
1.4 风机运行状态模拟
本文分析中将风机系统分两部分考虑,即将海床表面以上部分和桩-土相互作用部分分别建模。风机运行状态下水平荷载会引起土体的侧向位移,因此分析中首先在桩-土模型顶端施加侧向位移进行pushover分析以模拟风机运行状态,从而可以计算得到不同侧向位移下桩顶的力-位移曲线。
海床表面以上部分的底端水平向采用线性弹簧单元,其余方向固定约束,其中海床表面土体不同侧向位移状态下的等效弹簧系数通过上一步pushover分析获得的力-位移曲线计算得到,即等效弹簧系数等于力(F)除以相应的位移(u0)。
2 数值算例
本文以一5MW单桩式海上风机为研究对象,风机的相关参数由文献[16]和[30]获得。具体参数为:轮毅中心到海平面的高度为100 m,塔筒高度87.6 m,水深20 m,塔筒材料密度为8 500 kg/m3,桩体材料密度为7 850 kg/m3,弹性模量为210 GPa,剪切模量为80.8 GPa,吊篮的质量为2 40 t,转子(叶片+轮毅)的质量为110 t。
塔顶和塔底的直径分别为3.87 m和6 m,塔底和塔底的厚度分别为0.019 m和0.027 m;桩的直径为6 m,厚度为0.06 m。表1为风机水平面以上部分自振频率本文模型与文献[29]计算结果的比较,可以看出两者误差不超过5%。

表1 NREL 5MW风机自振频率Table 1 Natural frequencies of NREL 5MW wind turbine
图3为桩基入土深度(hs)不同时桩-土体系的力-位移曲线,由图中可以看出:极限承载力随入土深度的增加呈现先增加后减小的趋势。图4为沙土内摩擦角不同时桩-土体系的力-位移曲线,由图中可以看出:承载力随内摩擦角的增加而增加。
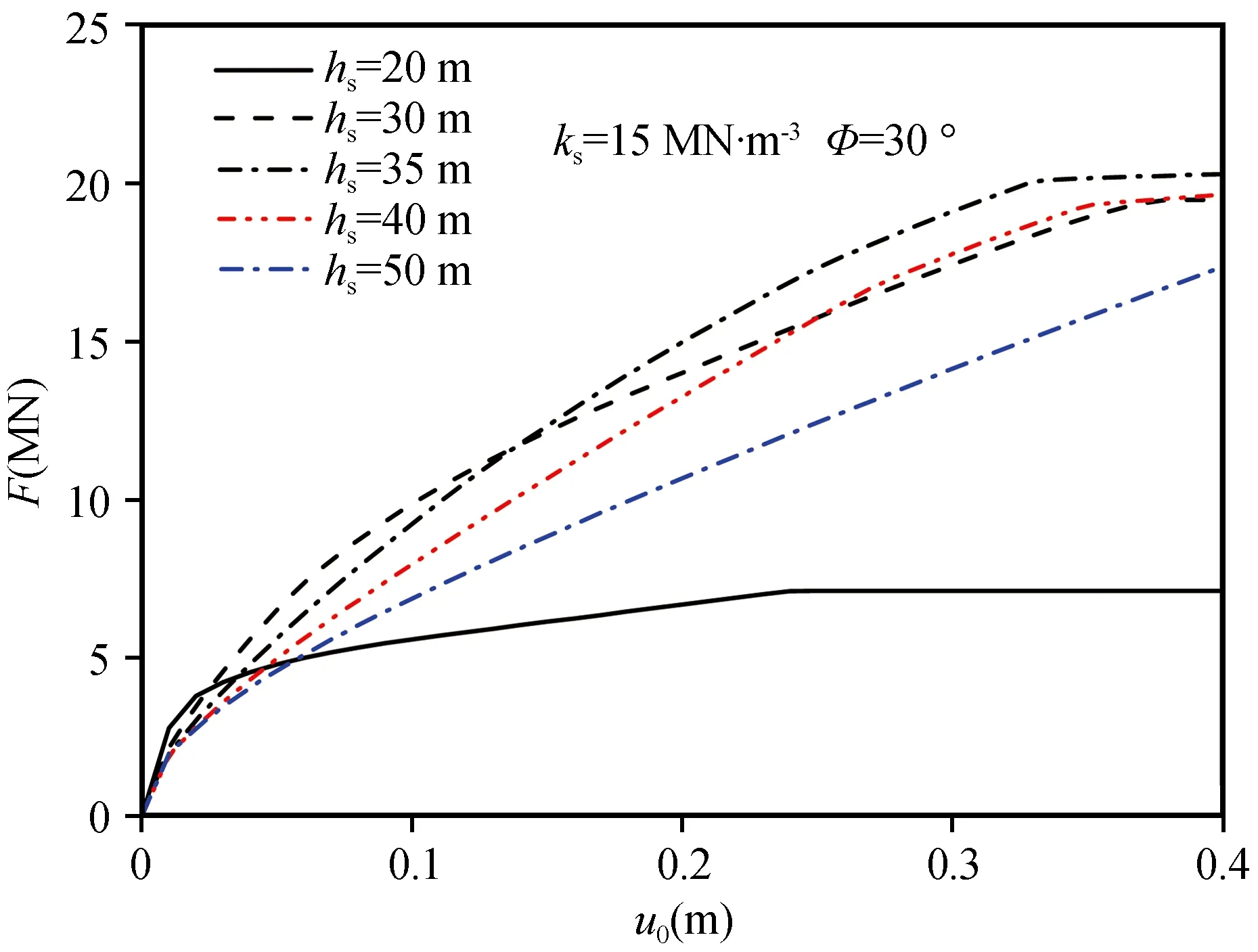
图3 桩基入土深度不同时桩-土体系的力-位移曲线Fig.3 The force-displacement curve of the pile-soil system for different pile depth in soil

图4 摩擦角不同时桩-土体系的力-位移曲线Fig.4 The force-displacement curve of the pile-soil system for different friction angle
图5为初始地基模量系数不同时桩-土体系的等效弹簧系数(k)随海床表面侧向位移的变化。由图中可以看出,等效弹簧系数随侧向位移的增加而减小,当加载位移较大时(u0>0.03 m)初始地基模量系数对等效弹簧系数的影响可忽略。
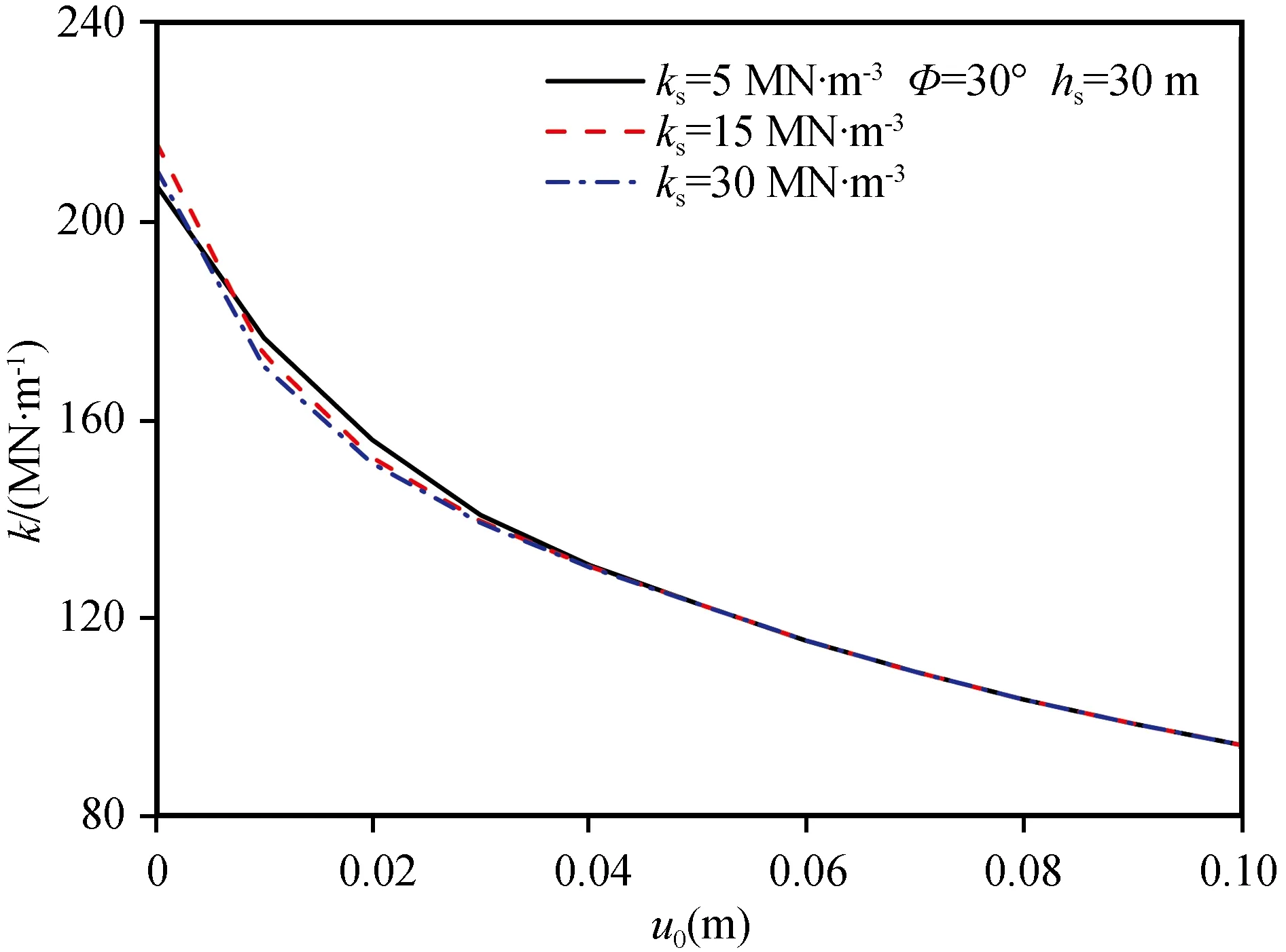
图5 初始地基模量系数不同时桩-土体系的等效弹簧系数Fig.5 The equivalent spring coefficient of the pile-soil system for different initial foundation modulus coefficient
定义参数Rf表示运行状态对风机结构体系自振频率的影响,Rf定义为侧向位移u0时的自振频率与无侧向位移时自振频率的比值。对图6为桩基不同入土深度时系数不同时一阶和二阶频率Rf随侧向位移u0的变化。由图中可以看出,随着侧向位移的增大,风机结构体系的自振频率逐渐减小;当桩基入土深度较小(hs=20 m)时,侧向位移u0对自振频率的影响更明显;侧向位移u0对一阶频率的影响较小,对二阶频率的影响显著。图7为二阶频率Rf随沙土摩擦角的变化,可以看出:侧向位移u0相同时,Rf随内摩擦角的增加而增大。

图6 桩基入土深度不同时Rf随u0的变化Fig.6 Rf varied with u0 for different pile depth in soil
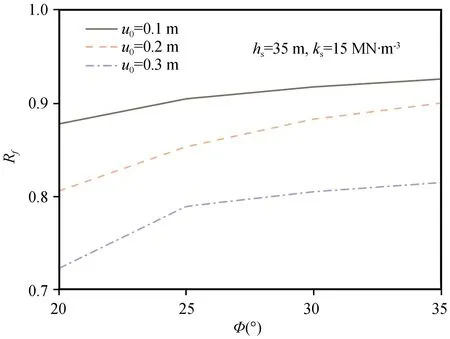
图7 u0不同时二阶频率Rf随φ的变化Fig.7 Second-order frequency Rf varied with φ for different u0
3 结论
本文基于数值方法讨论了大直径海上风机运行状态下体系的自振频率变化,风机运行状态通过海床表面桩基的侧向位移表示。计算结果表明:
(1) 桩-土体系的等效弹簧系数随侧向位移的增加而逐渐减小;桩基侧向位移会降低风机结构体系的自振频率。
(2) 桩基侧向位移对基频的影响较小,对高阶频率的影响显著;桩基入土深度较小时,桩基侧向位移对自振频率的影响更明显;桩基侧向位移对自振频率的影响随沙土内摩擦角的增大而减小。
(3) 总体来讲,在大直径海上风机的频率计算中可忽略风机运行状态对体系自振频率的影响。
