桩承式高速铁路路基的地震反应特性研究
2021-06-09宋永山彭晓东
宋永山,高 盟,彭晓东,徐 晓
(1.山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590;2.山东科技大学 土木建筑学院,山东 青岛 266590)
0 引言
随着我国高速铁路建设快速发展,高铁线路更加密集,而我国位于两大地震带,地震频发对高铁运行带来严重威胁[1],地震荷载作用下高铁的运行安全受到了广泛关注[2-3]。尤其是软土地区,桩承式路基以其优异性能在高速铁路建设中得到了推广和应用[4-6],因此研究地震荷载作用下桩承式路基的地震反应特性具有重要意义。
然而,目前对桩承式路基的研究多集中在列车移动荷载引起的路基动力反应特性,如周顺华等[7]分析列车瞬时冲击荷载作用下桩承式高速铁路路基土拱安定性,确定了土拱不发生累积变形破坏的荷载临界值;Thach等[8]建立桩承式路基有限元模型,分析了加固后路基与天然地基在列车移动荷载作用下的动力响应作用机理,发现路堤是控制振动响应的主要因素,且高频波会在桩支撑的路堤系统中被捕获和消散,从而显著降低路堤外的振动振幅;付强等[9]利用有限元法研究了列车荷载作用下PCC桩复合地基的动力响应,研究表明路堤内振动波远低于枕木处振动幅值,通过路堤、桩体和地基振动响应曲线体现了振动波在路堤系统各部分的传播特点;高广运等[10]通过2.5维有限元建立列车-轨道-路基整体动力分析模型,发现CFG复合路基减小了路堤边缘的高频振动,提高了路堤边坡的动力稳定性;薛富春等[11]精细化分析了轨道-路基-地基耦合系统的非线性振动响应。
而对地震荷载作用下路基动力反应特性的研究主要针对高速铁路桥梁桩基和公路路基。如陈令坤等[12]基于有限元法研究了不同地震强度下是否考虑桩土作用的高铁简支梁桥动力响应;刘闯等[13]通过振动台试验,分析了地震动强度下大直径桥梁嵌岩桩基础加速度、相对位移、弯矩等响应特性和损伤情况;赵建斌等[14]建立三维桩承式公路路基数值模型,研究了水平地震荷载作用下土工格栅抗拉模量和桩间距的影响;薛富春等[15]建立三维数值分析模型研究了桥梁-桥墩-桩基础-地基为一体的耦合系统的非线性地震反应。对桩承式高速铁路路基地震反应特性的研究鲜有文献报道。
1 计算模型及参数
1.1 有限元模型建立
依据《高速铁路设计规范》(TB10621-2009)[16],本文采用CRTSⅠ型板式无砟轨道,轨道结构从上向下依次为:钢轨、轨道板、CA砂浆层和底板。基床表层采用级配碎石,厚度为0.4 m,基床底层采用A、B组土,厚度为2.3 m,路堤采用A、B、C组土,厚度为2 m。模型剖面示意图如图1所示。

图1 模型剖面示意图Fig.1 Profile of calculation model
基于ABAQUS数值计算软件,建立轨道结构-路基-地基三维有限元模型,如图2所示。模型沿线路纵向的长度52 m,地基表面宽度52 m,总高度27.706 m。此模型系统由钢轨-扣件-轨道板-CA砂浆层-底板-基床表层-基床底层-路基本体-桩-地基组成。其中,钢轨采用60 kg·m-1标准钢轨,轨距为1.435 m;扣件支点间距为0.65 m;钢轨和扣件之间采用弹簧阻尼器进行模拟,扣件刚度的横向、垂向及纵向等效刚度分别为37.5、25、37.5 kN·m-1,阻尼系数分别为30、37.5、30 kN·s·m-1;轨道板、CA砂浆层、路基和地基均采用8结点实体单元。将地基土视为弹塑性材料,在桩-土界面上设置接触,对土体采用D-P模型,桩体采用弹性模型,桩-土之间设置接触对,包括法向作用(“硬接触”)和切向作用(摩擦特性为“罚”),单元选择线性减缩积分单元(C3D8R)。

图2 有限元计算模型Fig.2 Finite element computing model
为得到轨道、路基的振动响应规律,本文设置4个监测点,分别为轨道(监测点1)、基床表层(监测点2)、路肩边(监测点3)和路基坡脚(监测点4),如图3所示。
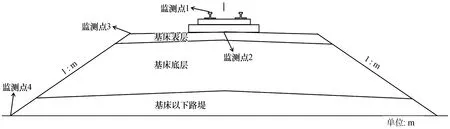
图3 监测点布置示意图Fig.3 Schematic diagram of monitoring point layout
1.2 地震荷载施加
夏栋舟等[17]在计算结构抗震性能分析时,将地震波加速度直接从模型底部输入,得到了合理的结果,本文亦采用该方法。从模型底部输入Imperial Vally地震波,选取抗震设防烈度为Ⅶ度,根据抗震设防烈度和地震动峰值加速度值的对应表(表1),将地震波峰值调整至0.1g,其水平方向加速度时程曲线如图4所示。取地震加速度时程曲线2~3.2 s加速度从模型底部输入,经计算,此时地面的加速度峰值约为0.13g,相当于烈度为Ⅶ度的地震。
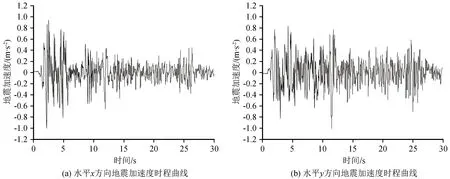
图4 Imperial Vally 地震加速度时程曲线Fig.4 Acceleration time history of Imperial Vally

表1 抗震设防烈度和地震动峰值加速度值Ag对应表Table 1 Ag corresponding table of seismic fortification intensity and peak acceleration of ground motion
1.3 边界条件
地震荷载作用下的动力分析属于半无限空间问题,为减小误差,需要在边界上设置人工边界。杜修力等[18]提出在边界每个方向添加单向弹簧-阻尼元件,以黏性阻尼吸能作用和弹簧刚性恢复作用模拟无限介质对近场的影响。采用其方法,地基四个侧面采用黏弹性边界,地基底部采用固定竖向位移的形式,模拟波从有限域向无限域传播。三维黏弹性人工边界的弹簧-阻尼元件参数为:
法向:

美国FATCA的CAA,虽然形式上是双边的对等协议,但实质上主要是向美国单向交换信息,很不公平。美国以推进FATCA为理由,至今未签署,也未承诺执行AEOI的CRS MCAA。美国在受益所有人审查和登记方面并未形成有效的国内立法,其结果,就是美国让上百个国家在其主导的规则下为国际税收信息自动交换相互博弈,却把自己保护起来成为安全岛,使美国成为全世界最大的避税港之一。
(1)
切向:
(2)
式中:ρ为介质密度;cp=[(λ+2G)/ρ]0.5,cs=(G/ρ)0.5分别为压缩波和剪切波的波速;A为平面波和散射波的幅值含量的比值;B为物理波速与视波速之间的关系;A和B可以通过数值试验经验获得,一般A=0.8,B=1.1;长度r为近场结构几何中心到该人工边界点所在边界线或面的距离。
1.4 模型计算参数
参考文献[19],有限元模型由钢轨-扣件-轨道板-CA砂浆层-底板-基床表层-基床底层-路基本体-地基组成。参考文献[19],除地基土外计算模型各组成部分采用弹性本构,模型边界采用三维黏弹性人工边界,计算参数列于表2。

表2 有限元模型计算参数Table 2 Parameters of the finite element computing model
2 计算模型验证
轨道-路基-地基有限元模型的有效性是结果准确的必要前提。董亮等[20]对高速铁路无砟轨道路基基床表层顶面竖向动应力进行了实测和数值模拟。对已建立的模型进行有效性验证,采用相同材料参数及列车轴重,得到基床表层竖向动应力对比图。如图5对比可知,本文所得基床表层动应力时程曲线与文献[20]结果基本吻合。

图5 与文献[20]对比结果Fig.5 Comparison between results of this paper and reference[20]
3 自由式路基振动响应规律
3.1 位移时程曲线分析
在自由式路基下施加地震荷载,研究轨道、路基的振动响应规律。如图6所示,为地震荷载作用下轨道和路基的位移时程曲线。对轨道不同方向,轨道x方向位移变化最大,最大位移为13.33 mm;z、y向分别为 2.62 mm、0.49 mm。水平x方向过大的位移无疑会在地震时导致轨道变形,威胁列车运行安全,如1976年中国唐山大地震(http://pic.enorth.com.cn/003/019/140/00301914051_6d98c759.jpg),需引起工程施工的重视。而对于路基各结构层,路基坡脚、路肩边、基床表层,从下往上z向位移最大值分别为12.6 mm、4.44 mm、0.5 mm,减小速度明显,说明路基在竖直方向有较好的减震作用。

图6 轨道和路基位移时程曲线Fig.6 Displacement time history curves of rail and subgrade
3.2 加速度时程曲线分析
图7为地震荷载作用下轨道和路基的加速度时程曲线。与位移时程曲线规律一致,轨道x方向加速度振幅最大,振幅峰值为0.71 m/s2,z方向为0.11 m/s2,y方向为0.09 m/s2。路基坡脚、路肩边、基床表层,从下往上加速度逐渐减小,z向加速度最大值分别为0.54 m/s2、0.2 m/s2、0.06 m/s2。振动加速度幅值在路基中衰减明显。
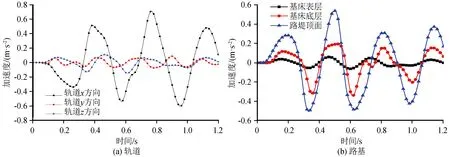
图7 轨道和路基加速度时程曲线Fig.7 Acceleration time history curves of rail and subgrade
3.3 频谱分析
频谱分析是抗震分析的重要手段之一,地震荷载作用下轨道和路基加速度频谱曲线如图8所示。得到地震作用下轨道和路基的频率主要集中在0~10 Hz,为低频振动。由图可知,轨道不同方向主频值及加速度值并不相同,x、z方向频谱曲线较为相似,主导频率均为2.9 Hz,频率范围为0~10 Hz,加速度最大值分别为0.39 m/s2、0.003 8 m/s2;y方向主导频率为4.4 Hz,频率范围为0~15 Hz,加速度最大值为0.003 7 m/s2。路基各层主导频率一致,均为2.9 Hz;但基床表层主要频率缩小到0~5 Hz,说明路基吸收了部分地震能量。而图10为输入地震波水平方向加速度频谱曲线,频率主要集中在0~15 Hz。x方向主导频率为0.8 Hz,加速度最大值为0.3 m/s2,地震波y方向主导频率为0.4 Hz,加速度最大值为0.29 m/s2。
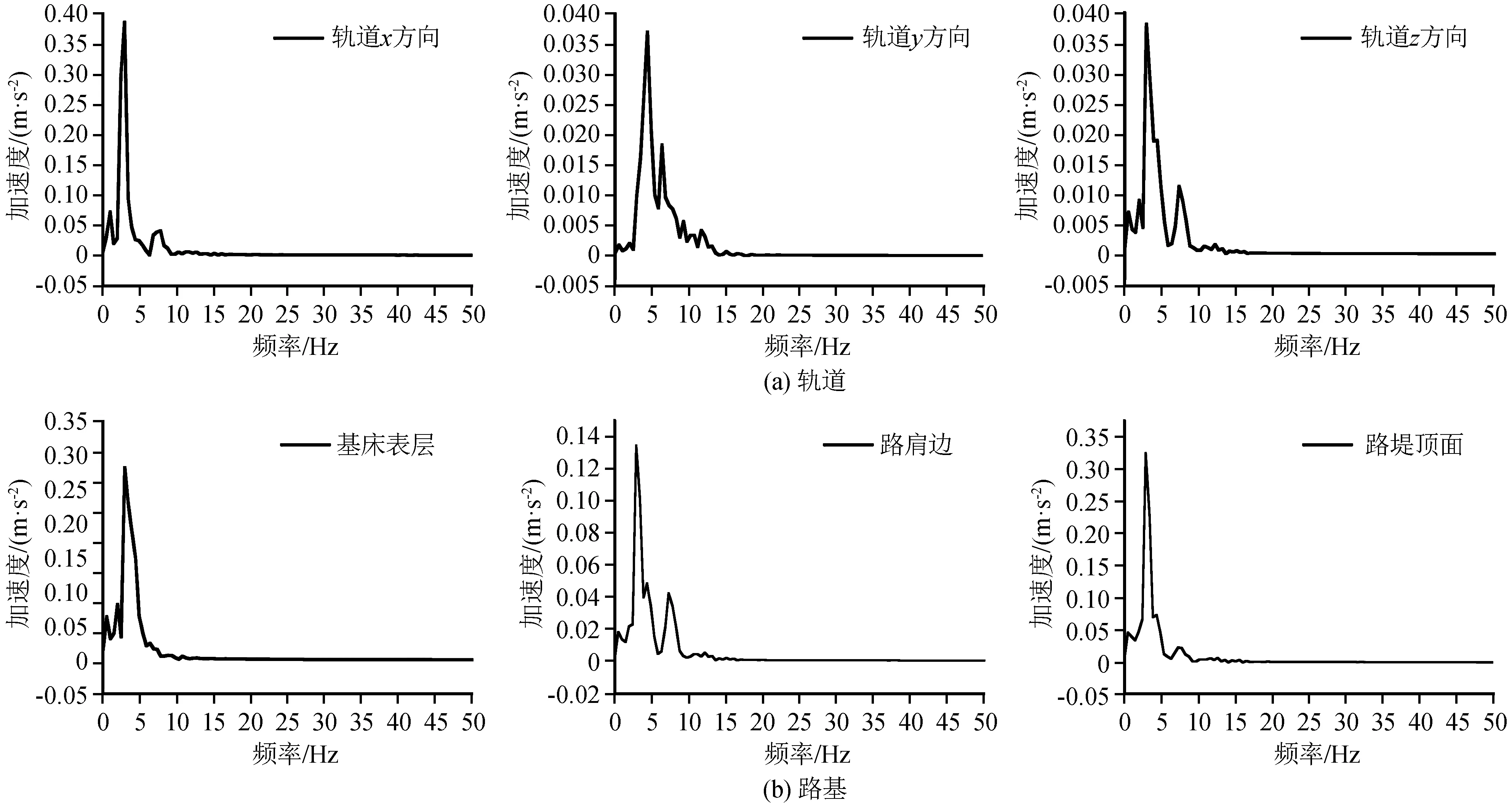
图8 轨道和路基加速度频谱曲线Fig.8 Acceleration spectrum curves of rail and subgrade
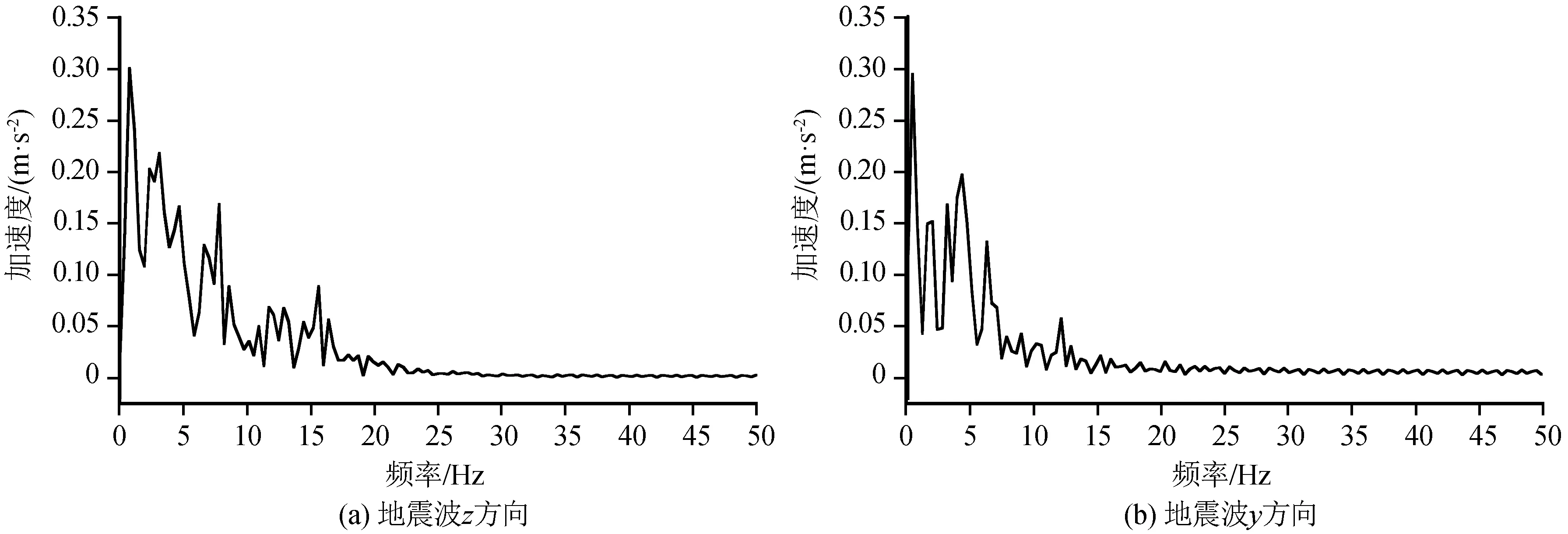
图9 地震波加速度频谱曲线Fig.9 Acceleration spectrum curves of earthquake wave
对比两图可知,地震波频谱曲线主导频率在1 Hz以下,且主频不唯一,频率范围为0.4~20 Hz。而轨道和路基频谱曲线主导频率比较单一,主频范围为2.5~7.5 Hz,频率范围为0~15 Hz。经过地基传播介质,地震波多个主频及15~20 Hz频率等特征的能量被吸收。
4 桩承式路基参数分析
4.1 桩径
为分析桩径对高速铁路路基抗震影响,设置桩间距为2 m,桩长为10 m,桩径为0.6 m,0.8 m,1.0 m及1.2 m进行计算,分析不同桩径时轨道和轨道中心正下方路基各层位移幅值变化以及加速度幅值变化情况。其中,桩径为0时表示地震荷载作用下的自由式路基。
由图10可知,钢轨x、y方向位移幅值随桩承式路基桩径增大而增大,而z方向位移幅值较自由式路基有所减小。对于路基各层,桩承式路基位移幅值明显减小,且随桩径增大而减小,但减小速率逐渐放缓。对比自由式路基,桩承式路基作为复合地基,抗弯刚度增大,且随桩径增大,复合地基置换率越大,路基、钢轨竖向位移减小。而桩体弹性模量增大导致地震能量吸收减小,则成为轨道水平位移增加的主要原因,桩承式路基的存在反而增加了列车脱轨的风险。

图10 桩径对轨道和路基各层位移幅值影响Fig.10 Influence of pile diameter on displacement of rail and subgrade
图11为轨道、路基加速度幅值随桩承式路基桩径变化情况。桩承式路基对地震加速度有较好的减弱作用,但并不是随着桩径增大而持续增强,当桩径过大,复合地基整体刚度过大时,轨道、路基加速度响应又开始增大。轨道x、z方向加速度幅值减小明显,但当桩径超过1.0 m时,轨道x方向又开始增大。轨道z方向加速度幅值最低点出现在桩径0.8 m。而路基各层位移幅值同样随桩径增大先减小后增大。
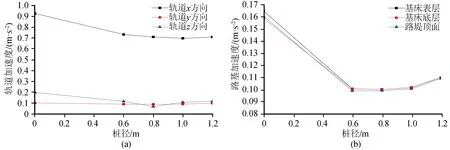
图11 桩径对轨道和路基各层加速度影响Fig.11 Influence of pile diameter on acceleration of rail and subgrade
4.2 桩长
设置桩间距为2 m,桩径1.0 m,对桩长分别为8 m,10 m,12 m,14 m的桩承式路基的动力响应特性分析。
图12为轨道和路基位移幅值随桩长变化规律,桩承式路基轨道x方向位移幅值随桩长增大而增大,而y、z方向只有较小幅度的减小作用。同样,桩体增加对轨道x方向位移仍存在增大效应。对于路基各层,桩承式路基中各监测点位移幅值明显减小,桩长越长,桩侧阻力越大,z向位移幅值越小。
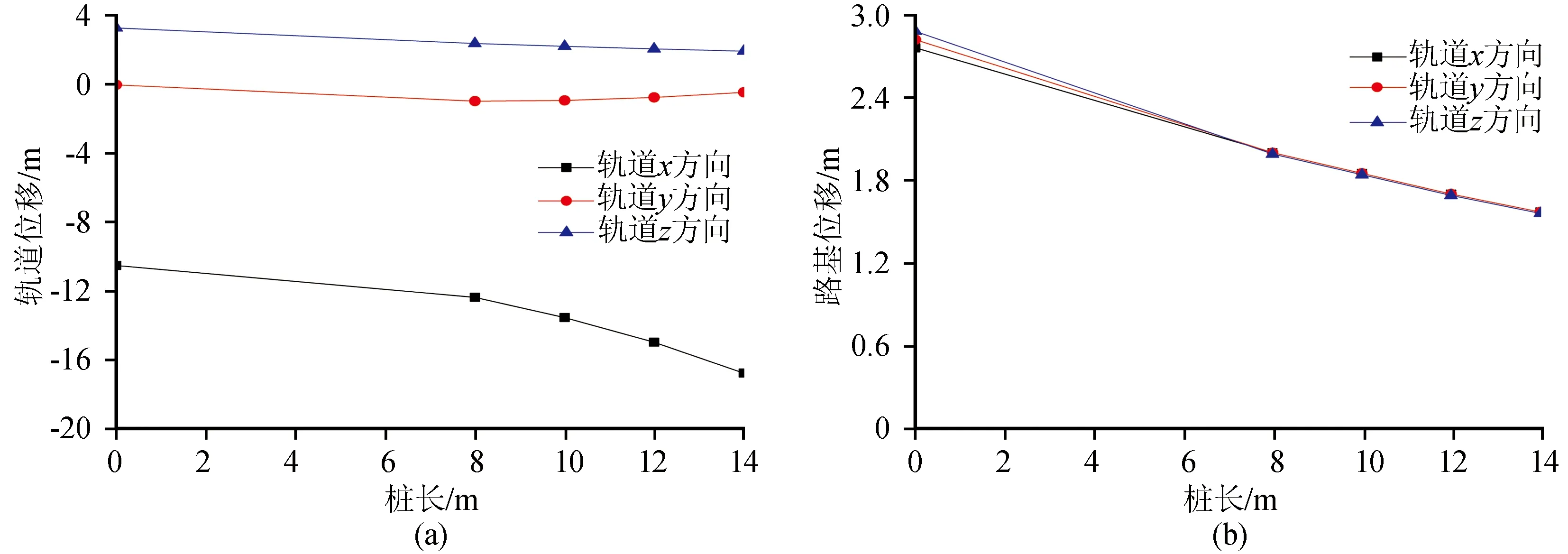
图12 桩长对轨道和路基各层位移幅值影响Fig.12 Influence of pile length on displacement of rail and subgrade
对比自由式路基,桩承式路基轨道、路基加速度幅值减小明显,如图13所示。但轨道x方向加速度幅值在桩长为8 m时最小,之后随桩长增大而增大。轨道z方向、路基各层加速度幅值随桩长增大有效减小,桩长越大,桩土有效接触面积越大,地震加速度吸收越多,轨道路基z向加速度越小。
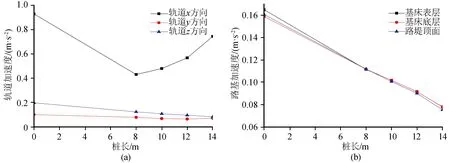
图13 桩长对轨道和路基各层加速度影响Fig.13 Influence of pile length on acceleration of rail and subgrade
4.3 桩间距
桩间距同样是影响桩承式路基减震效果的重要因素。设置桩长为10 m,桩径1.0 m,桩间距分别为1.5 m、2 m、2.5 m和3 m进行计算。
图14、15为轨道和路基振动响应随桩间距变化规律。研究表明在2.5D范围桩间距内群桩效应明显,因此,轨道x、y方向位移幅值随桩间距增加先增大后减小,在桩间距2 m时出现最大值,桩间距的加大对桩体弹性模量的集中增大起到了一定的减弱作用,因此超过2 m后桩间距越大,x、y方向位移幅值越小。而桩间距不断增大对z向位移的减震效果却起到了减弱作用,路基各层位移幅值随桩间距增大先减小后增大,桩间距2 m时位移幅值出现最小值。对于加速度幅值,轨道x、z方向随桩间距增大呈现先减小后增大的趋势。且两者在桩间距为2 m时出现最小值。路基各层加速度幅值随桩间距增大先减小后增大,最低点在1.5 m。

图14 桩间距对轨道和路基各层位移幅值影响Fig.14 Influence of pile spacing on displacement of rail and subgrade

图15 桩间距对轨道和路基各层加速度影响Fig.16 Influence of pile spacing on acceleration of rail and subgrade
4.4 桩身材料属性
设置桩间距为2 m,桩长为10 m,桩径1.0 m,桩弹性模量分别为10 GPa、15 GPa、20 GPa、25 GPa和30 GPa进行计算,分析不同桩弹性模量时轨道和路基各层位移幅值及加速度幅值变化。
由图16可知,轨道x方向位移幅值随桩弹性模量增大而增大,同样证实,桩弹性模量增大使地基刚度变大是导致桩承式路基较自由式路基轨道横向位移变大的原因。而轨道z向位移幅值随桩弹性模量增大而减小。路基各层z向位移幅值随桩弹性模量增大逐渐减小。
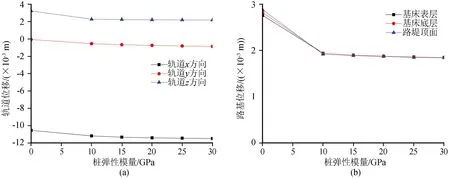
图16 桩弹性模量对轨道和路基各层位移幅值影响Fig.16 Influence of pile elastic modulus on displacement of rail and subgrade
由图17可知,桩承式路基状体弹性模量增大有效减小地震加速度。轨道x、z向加速度随桩弹性模量增大而减小,路基各层加速度也随桩弹性模量增大而逐渐减小,但减小速率很小。桩体弹性模量增大到10 GPa后,路基、轨道加速度减弱效果便不再明显。

图17 桩弹性模量对轨道和路基各层加速度影响Fig.17 Influence of pile elastic modulus on acceleration of rail and subgrade
5 结论
本文建立地震荷载作用下高铁路基三维有限元模型,分析了自由式路基的振动响应规律,并对桩承式路基的桩体参数进行分析,得到了一些具有工程应用价值的结论。
(1) 地震荷载作用下,自由式路基轨道x方向位移变化最大,最大位移为13.33 mm;加速度振幅也最大,最大值为0.71 m/s2;而对于路基各结构层,从下往上位移幅值、加速度幅值减小明显;频谱曲线表明,轨道和路基主频单一,主导频率范围为2.5~7.5 Hz,主要为低频振动,经过地基传播介质,地震波多个主频及15~20 Hz频率等特征的能量被吸收。
(2) 地震荷载作用下,桩承式路基对x方向位移幅值、加速度幅值反而有增大作用,可能会导致列车脱轨;但对路基及轨道z向有较好的减小作用,有利于减小沉降。
(3) 综合分析各项桩体参数变化对地震荷载作用下桩承式路基的动力响应,最佳桩径约为0.8 m,最佳桩长为8~10 m,最佳桩间距为1.5~2 m,最佳桩弹性模量为20 GPa。
