基于分布式模型预测控制的含分布式储能有源配电网动态电压控制

李桂鑫，徐科, 刘英英，吕永青，窦晓波，迟福建

(1.国网天津市电力公司，天津市 300010；2.东南大学电气工程学院，南京市 210096)

0 引 言

近年来随着大规模分布式电源(distributed generator,DG)接入配电网，虽然改善了配网侧的用能结构，缓解了电网的用电压力，但是也可能使配电网用户的电能质量下降[1-3]。分布式电源的不确定功率出力剧烈波动可能会导致配电网潮流变化和电压突变，短时间的电压越限问题频发，如天气突然变化导致光伏发电突增或骤减，光伏发电达到峰值阶段与用户负荷用电峰值时间不匹配。此外，光伏发电受天气影响明显，其逆变器容量难以充分利用，中低压配电网线路通常呈阻感特性，功率耦合也提升了快速电压恢复的难度。

目前分布式电源大量接入配电网，带来的不确定性使配电网的电压控制问题引起了学者的广泛关注。分布式电源的有功和无功功率可同时参与电压调节。有功功率调压可通过光伏进行有功功率削减或储能有功功率调节的方式使电压保持在安全偏差以内。文献[4]针对储能变流器有功控制，提出一种基于相位同步的控制器状态切换控制策略，保证储能参与电压调节时的有功功率调节指令精确跟踪。文献[5]通过在配电网末端接入用于系统调压等辅助服务的储能系统，应对可再生能源及负荷波动导致的电压运行水平问题。

此外，通过各类换流器的相角旋转可产生无功功率，使分布式电源参与电网的无功优化，这是配电网调压的重要环节之一。文献[6-7]基于分层结构并充分利用配电网有载调压变压器、分布式电源以及电容器等设备实现电压越限的调节，实现多类调压设备的有功和无功功率协同配合。文献[8]针对低压分布式光伏参与整体协调优化的问题，提出一种多电压层级配电网无功电压协调精准控制策略。以上研究未能利用光伏逆变器剩余容量，且未发挥储能有功和无功功率四象限出力的优势，未充分挖掘分布式电源参与电压控制的潜力。

为了更好地利用分布式光伏、储能等资源并网后的动态调节能力，迫切需要更先进的控制方法。文献[9]提出基于模型预测控制(model predictive control, MPC)的全局优化和区域自治的电压控制方法，能有效应对分布式电源波动带来的电压越限问题。文献[10]提出一种基于MPC的多时间尺度电压协调控制策略，实现有载变压器、电容器组、分布式电源等快慢设备协同调压。但以上研究多基于稳态模型进行控制，没有考虑设备动态控制过程以及弱电网耦合特性下的设备协同配合。

本文设计基于分布式模型预测控制的含分布式储能有源配电网动态电压控制方法，发挥分布式光伏和储能有功无功功率的灵活调节能力，实现电压越限的快速恢复控制。具体研究如下：针对光伏和储能不同的本地工作方式建立其动态模型；结合配电网电压灵敏度模型，通过ε分解法将整体配电网进行区域划分，构建各子区域的分布式电压控制模式，实现配电网不同区域间的系统解耦；根据形成的分布式电压控制结构，设计分布式模型预测控制方法，实现配电网电压越限的动态恢复，并保持在控制过程中对分布式光伏出力限制、分布式储能荷电状态(state of charge, SOC)限制等运行约束的良好兼顾。

1 基于分布式光伏和储能动态特性的配电网络模型

1.1 分布式光伏动态模型

分布式光伏的特性在于有功功率通常基于最大功率点跟踪(maximum power point tracking,MPPT)控制而无法任意调节[11-13]，利用无功功率实现QPV(V)控制(以光伏并网点电压V作为控制输入量实现逆变器无功功率QPV调节)如图1所示。

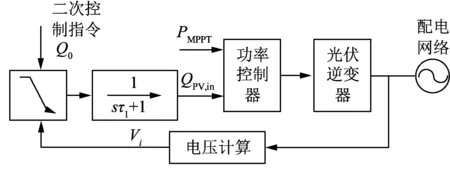
图1 分布式光伏动态模型Fig.1 Dynamic model of distributed PV

图1中：PMPPT为光伏MPPT输出功率；τ1为滤波器常数；QPV,in光伏逆变器输入无功功率；Vi为并网点电压；Q0为二次控制指令；s为微分算子。

通过沿无功功率Q轴调整Q(V)特性，以保持死区宽度和最大无功功率注入/吸收值(Qmax)为常数，即本地根据Q(V)特性进行调整，当接收到二次电压控制器的无功功率设定点(Q0)时，按图2所示规则执行。

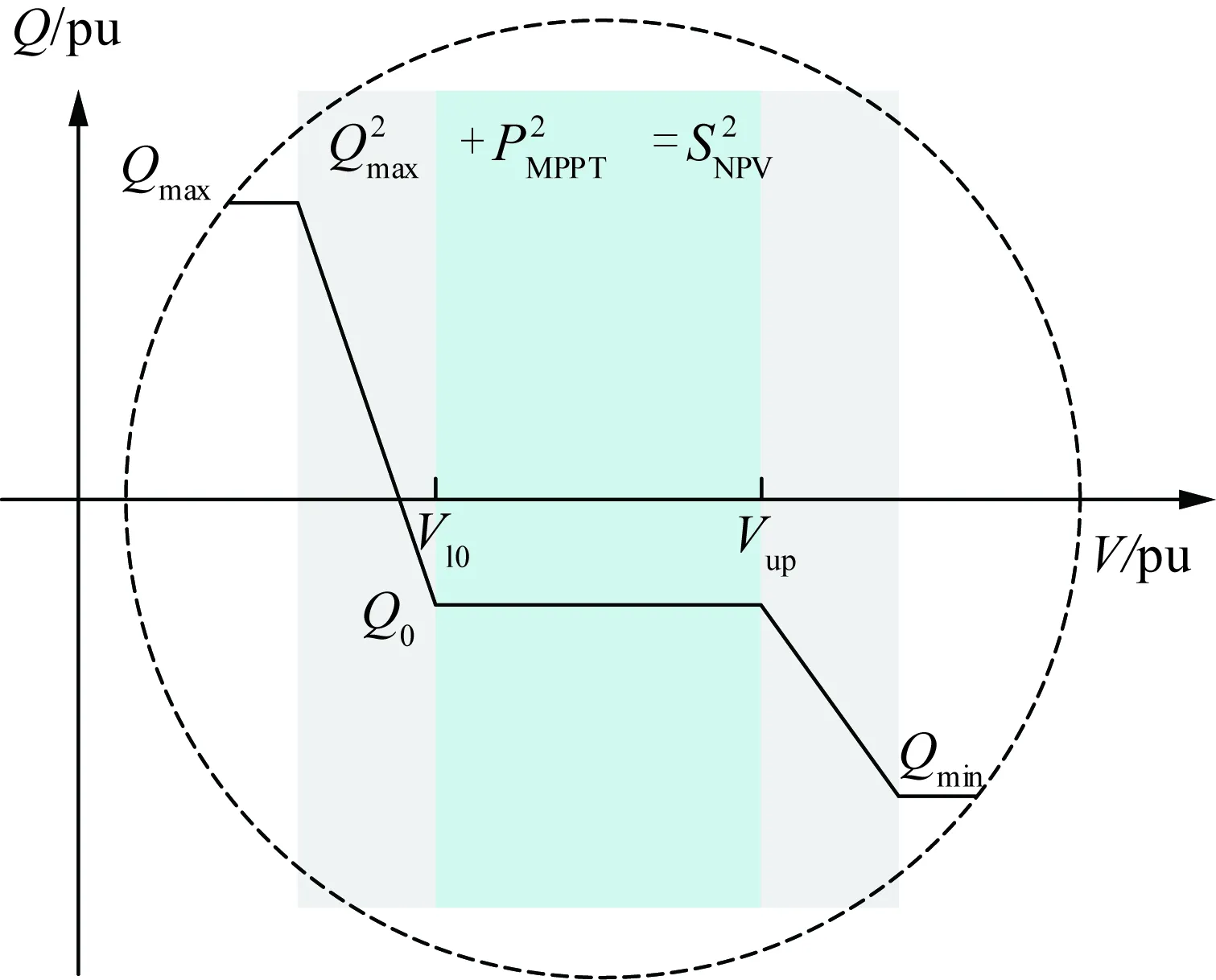
图2 光伏Q(V)调节特性Fig.2 Q-V characteristic of PV

根据上述模型建立分布式光伏系统出力的状态空间方程：

(1)

式中：TPV为光伏时间常数；PPV、Qi分别为光伏逆变器输出有功、无功功率；Kd为无功电压下垂系数；Vref为电压参考值。

将模型式(1)离散化并写成状态空间方程：

xPV(k+1)=APVxPV(k)+
BPVuPV(k)+BdPVdPV(k)

(2)

式中：k为采样时刻；xPV(k)为分布式光伏状态量；uPV(k)为分布式光伏控制量；dPV(k)为分布式光伏扰动量；APV为分布式光伏系统矩阵；BPV为分布式光伏控制矩阵；BdPV为分布式光伏扰动矩阵。

1.2 分布式储能动态模型

储能系统的特性受到电池SOC影响，忽略其充放电损耗，则SOC部分模型为：

(3)

式中：Soc(k)为k时刻储能荷电状态；Ts为采样时间长度；Emax为储能最大容量；PBESS(k)为储能输出有功功率。

由于储能有功无功功率同时参与二次电压控制，故本地控制部分采用PQ控制方式，能够快速跟踪二次控制指令[11]，如图3所示。

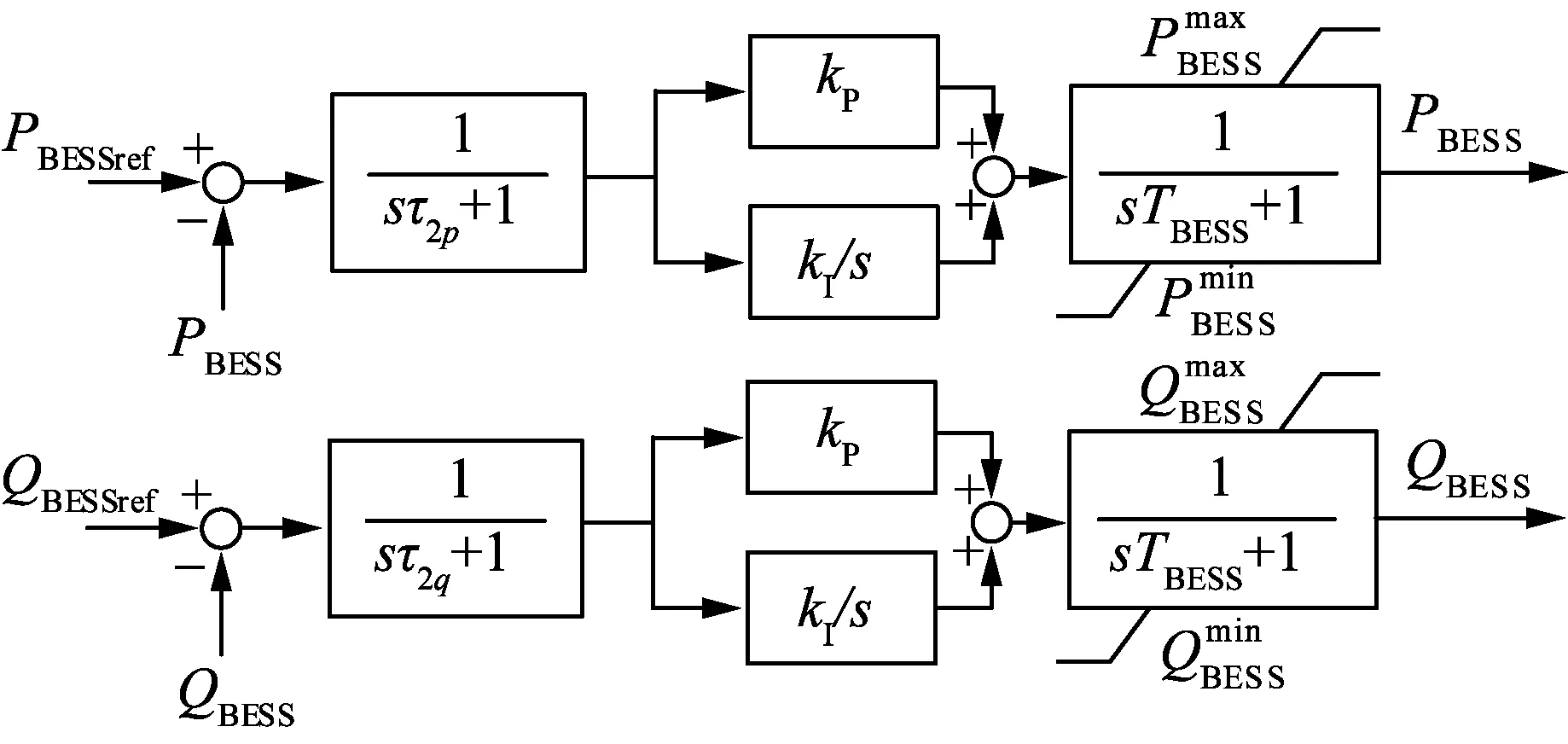
图3 分布式储能动态模型Fig.3 Dynamic model of distributed ES

则储能系统的动态模型为：

(4)

式中：PBESS,in、QBESS,in分别为储能变流器输入的有功和无功功率；PPI、QPI为PI控制器输入的有功和无功功率。

将储能模型式(4)离散化并写成状态空间方程形式：

xES(k+1)=AESxES(k)+BESuES(k)

(5)

式中：xES(k)为分布式储能状态量；uES(k)为分布式储能控制量；AES为分布式储能系统矩阵；BES为分布式储能控制矩阵。

1.3 配电网络动态模型

对配电网络的建模，在给定的工作点附近可以通过计算关于控制输入和扰动的电压灵敏度矩阵来确定，描述分布式电源功率和电压变化之间的线性关系[14-15]：

(6)

式中：ΛθP、ΛθQ、ΛVP、ΛVQ表示电压灵敏度系数；Δθ、ΔV分别为部分节点的相角、电压偏差量；ΔP、ΔQ分别为分布式光伏和储能连接节点的注入有功和无功功率。则控制后的电压关系为：

Vr=V0+ΛVQ·xQ+ΛVP·xP

(7)

式中：V0、Vr为某节点调整前后的初始电压和参考电压；xQ=Qr-Q0，其中Q0、Qr为某节点电压调整前后DG的无功功率输出；xP=Pr-P0，其中P0、Pr为某节点电压调整前后DG的有功功率输出。

将式(7)写成如下形式：

Vi(k+1)=Vi(k)+ΛESCES[(AES-I)xES(k)+

BESuES(k)]+ΛPVCPV[(APV-I)xPV(k)+

BPVuPV(k)+BdPVdPV(k)]

(8)

式中：Vi(k)为k时刻节点i的电压矩阵；ΛES、ΛPV表示分布式储能、光伏对应所调控节点电压的灵敏度矩阵；CES和CPV分别为分布式储能和光伏的输出矩阵；I为单位矩阵。

结合式(2)(5)(8)，建立含分布式电源动态特性的配电网整体状态空间方程：

x(k+1)=Ax(k)+Buu(k)+Bdd(k)

(9)

式中：x(k)为配电网整体状态量；u(k)为配电网整体控制量；d(k)为配电网整体扰动量；A为配电网整体系统矩阵；Bu为配电网整体控制矩阵；Bd为配电网整体扰动矩阵。

2 基于分布式模型预测控制的电压控制设计

2.1 基于ε分解的配电网络解耦方法

为避免对通信可靠性过高的要求，将系统分解为若干子系统进行分布式控制。通过ε分解法将一个大系统分解为若干弱耦合子系统[16]，以子矩阵ΛVP为例：

ΛVP=Λ′VP+ε·R

(10)

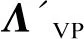
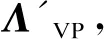
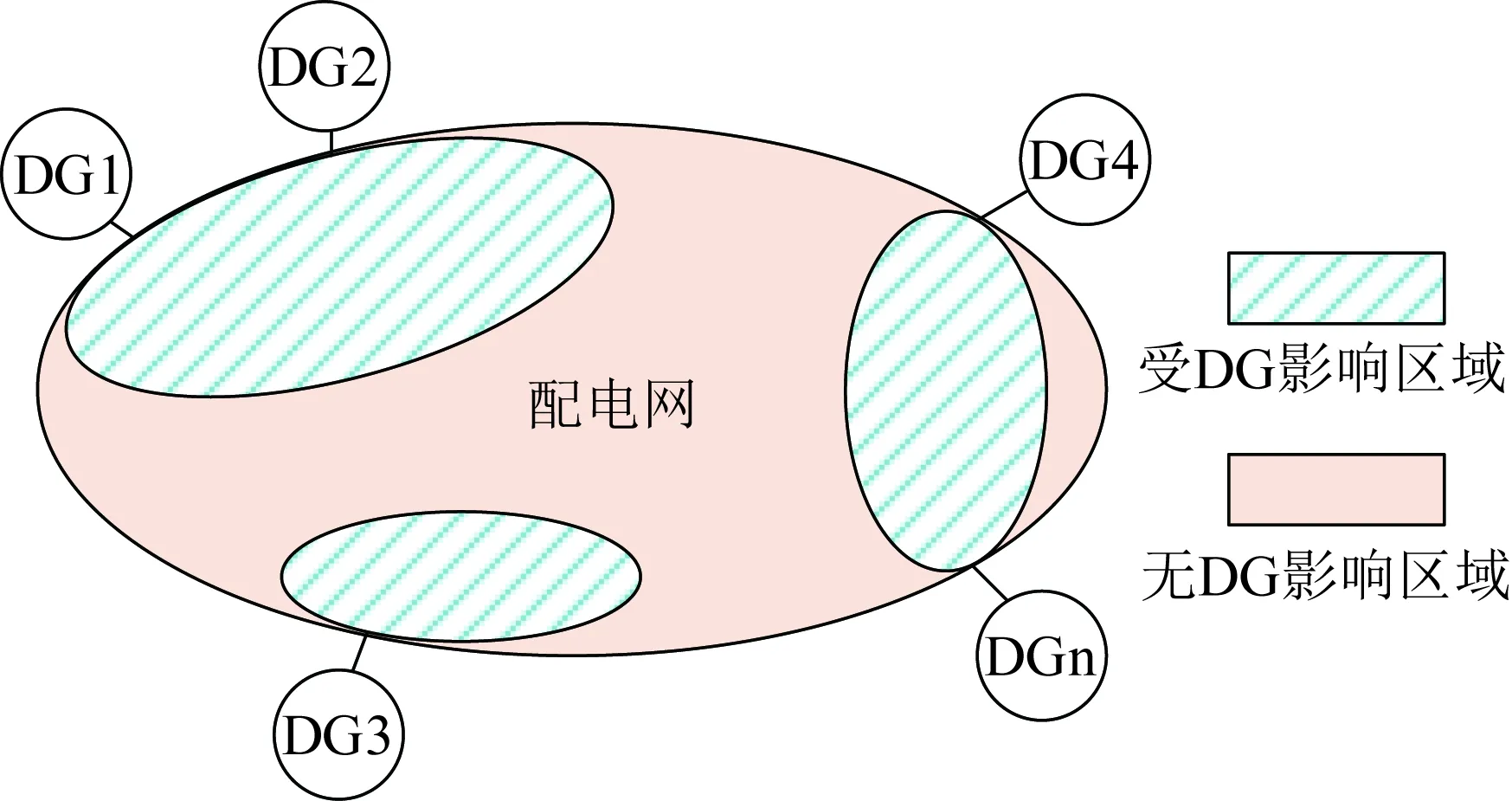
图4 分布式电源影响区域示意图Fig.4 Influence zone of distributed generators

2.2 控制约束条件

在控制实施的过程中，各类分布式电源不同特性导致其出力具备不同的约束情况需要考虑[18]。

一般情况下，控制输入的变化量计算如下：

Δu(t)=u(t)-u(t-1)

(11)

式中：u是控制输入通过测量得到的近似值。考虑动态调压过程中各类设备的物理限制形成以下各控制变量约束：

(12)

(13)

(14)

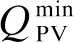
(15)

(16)

式中：SNBESS为储能变流器额定容量；SNPV为光伏逆变器额定容量。

考虑储能SOC和电压偏差调节效果，将其作为输出约束对控制予以限制：

ΔVmin≤ΔV≤ΔVmax

(17)

(18)

2.3 基于DMPC的动态电压控制方法

模型预测控制是在当前时刻，考虑系统未来有限时间的状态变化，并使用当前时刻的测量值和预测模型，得到当前和未来有限时间的最优控制序列。而在下一时刻，利用当前时刻实施控制后的状态数据重复这一过程。同时模型预测控制能够直接考虑控制过程中相关的状态、输入和输出变量的约束条件，控制器的设计直接体现被控过程的动态过程。模型预测控制的原理如图5所示。

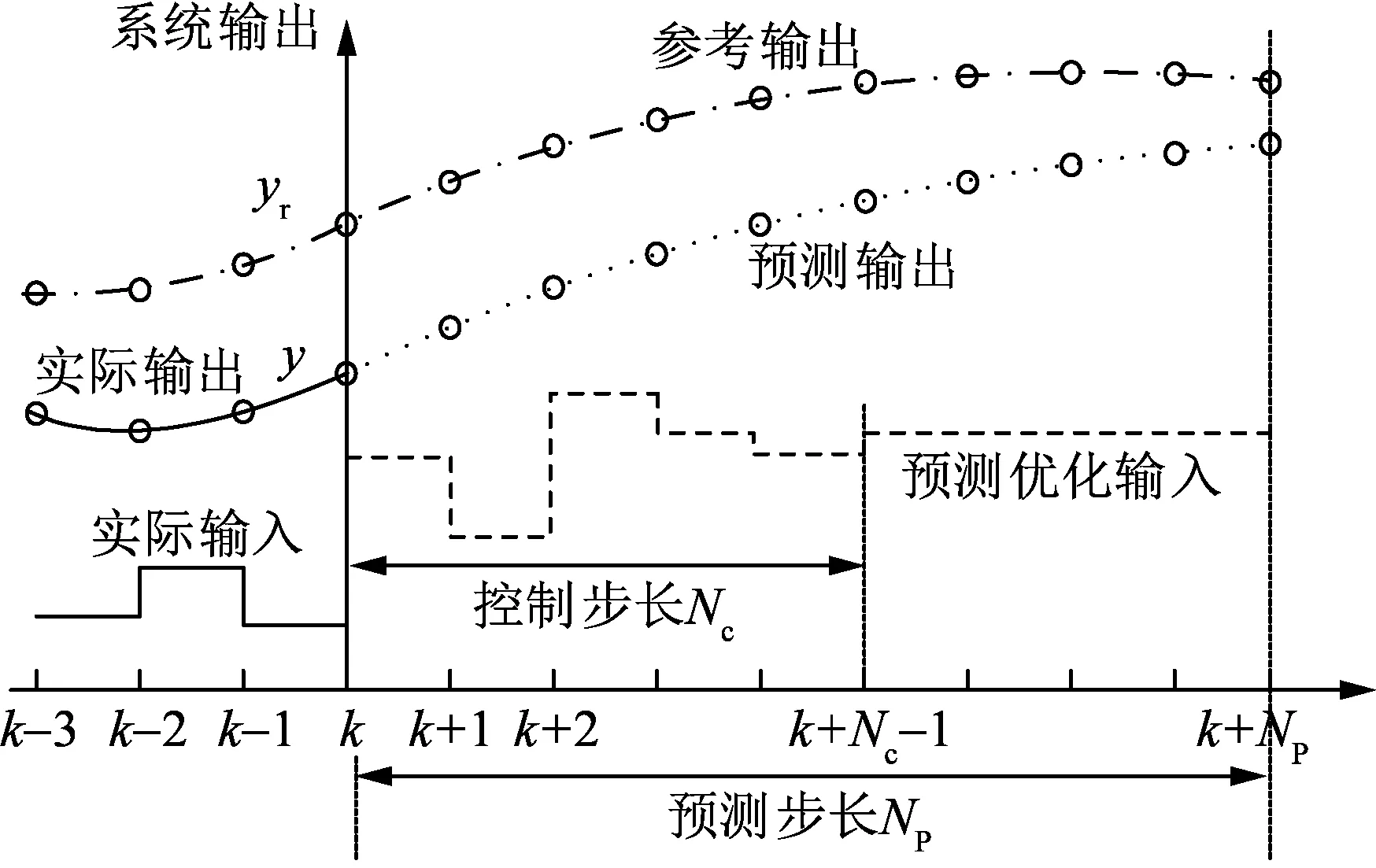
图5 模型预测控制原理图Fig.5 Schematic diagram of MPC

分布式预测控制在建立子系统模型时，考虑子系统之间的状态数据交互，每个子系统都会获得一部分其他子系统信息，并能够预测未来短时间内子系统间的相互影响。为便于电压控制设计，将配电网整体模型写成如下形式[19]：

(19)

式中：xi(k)、ui(k)、yi(k)、di(k)分别为第i个子系统的状态量、控制输入量、输出量、扰动量；Ai、Bi、Ci、Di分别为第i个子系统的系统矩阵、控制矩阵、输出矩阵和扰动矩阵；Aij为第i个和第j个子系统的耦合矩阵。如果矩阵Aij不为空矩阵，则表示第i个和第j个子系统耦合的，两者互为相邻系统。根据预测控制基本原理，可基于模型式(19)预测系统未来的动态。为此，设定系统预测时域为Np，控制时域为Nc且Nc≤Np。在当前时刻k，可以计算Δx(k)=x(k)-x(k-1)，并以此作为预测系统未来动态的起点，由式(19)可预测系统状态如下[19-20]：

(20)

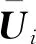
(21)

式中：Ri、Ei、Fi为加权矩阵。

由于约束条件的存在，无法直接求得控制律的解析式，所以将MPC中含约束优化问题求解转化为二次规划问题求解，令ηi=Εi+Fi，将式(21)表示为：

(22)

电压偏差约束和储能电池SOC约束为输出约束，通过预测方程转化为控制约束：

(23)

式中：Su,bi、Sx,bi、Sx,bij、Sd,bi为约束矩阵；Ymax、Ymin为输出约束向量。

结合2.2节中控制约束条件，将式(22)转化为二次约束二次规划(quadratically constrained quadratic program, QCQP)，描述如下：

(24)

式中：Cu、b(k+1|k)分别表示约束矩阵和向量。

由此，通过含约束的分布式模型预测控制设计，对配电网进行动态电压控制，实现节点电压越限的快速恢复。

3 仿真验证

3.1 仿真参数

为验证所提基于分布式模型预测控制的含分布式储能有源配电网动态电压控制方法的有效性与可行性，在Matlab/Simulink平台中基于IEEE-33节点标准配电网线路参数与拓扑，同时参考国网天津市电力公司科技项目(电力物联网体系下的城市配电网多层级混合储能灵活优化配置技术研究)中对储能系统的安装计划与分布，类比实际天津城市配电网与IEEE标准配电网拓扑，进行分布式储能的选点与功率确定，据此建立含分布式光伏和储能接入的有源配电网模型，仿真试验拓扑如图6所示。按照本文中所介绍的ε分解方法对不同分布式电源进行影响范围确定，然后按照其影响范围进行就近归类与分区，具体线路及负荷参数见附录表A1—A2。

在配电网中接入12组可控分布式电源，编号如图6所示，包括位于节点6、10、17、18、24、26的分布式储能电源和位于节点4、9、15、18、22、30的6个分布式光伏电源，各分布式电源参数详见附录A表A3。

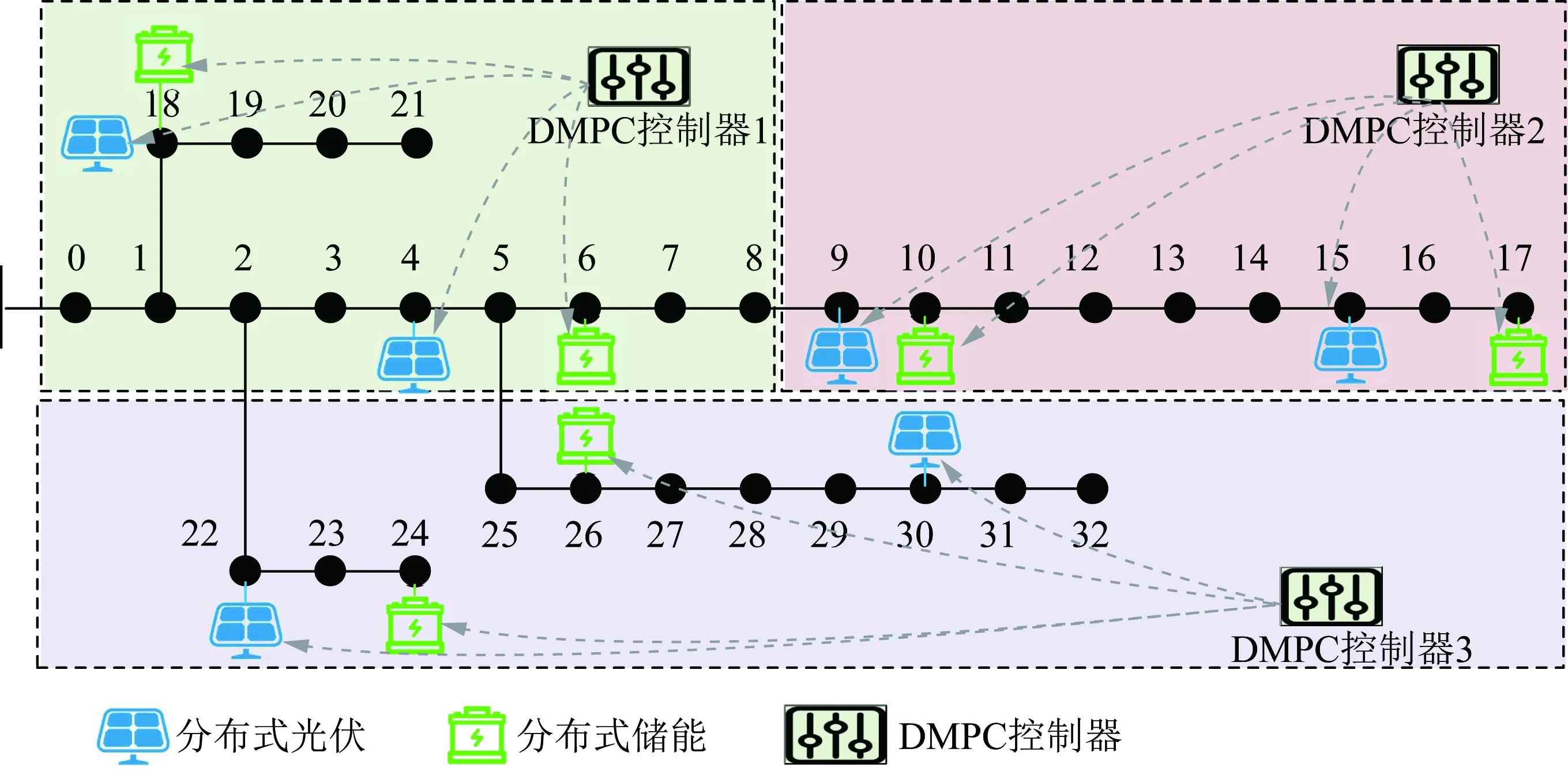
图6 基于IEEE-33节点有源配电网仿真试验拓扑Fig.6 Active distribution simulation test topology based on IEEE 33-node system

分布式光伏的有功功率出力为0～100%额定容量，其无功功率出力使功率因数不低于0.95；分布式储能的有功功率出力为0～100%额定容量，其无功功率出力为0～40%额定容量。单台设备有功功率出力波动不大于400 kW，分布式光伏、储能设备响应时间小于0.3 s，不设置通信延迟。

3.2 仿真分析

3.2.1场景1：潮流正向下光伏出力跌落

1)实际中仅本地支撑下系统电压水平。

为验证所提方法有效性，本文选取具有代表性的工况进行仿真验证。模拟天气由晴转阴，分布式光伏出力突然降低，即分别在4 s和12 s处设置光伏出力骤减，波形如图7所示。在此种工况下，仅用光伏和储能调压支撑，电压易发生越限问题，如图8所示。

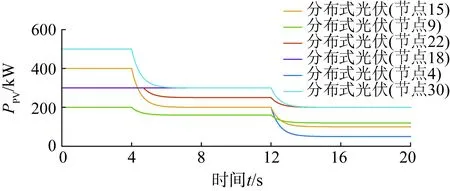
图7 场景1下各分布式光伏有功功率出力波形Fig.7 Active power output of PVs in case 1

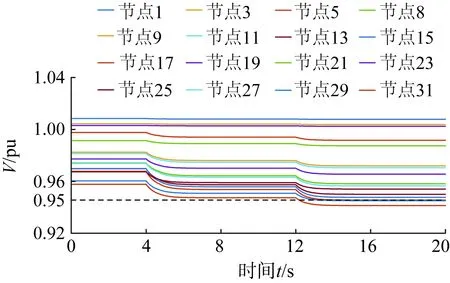
图8 场景1下IEEE-33节点拓扑内部分节点电压Fig.8 Voltage of some nodes in IEEE 33-node system in case 1

图8表示正向潮流无控制时IEEE-33节点配电网总体电压分布情况(选取16个节点电压，编号为2m+1，m=0、1、…、15)。由于在12.66 kV电压等级下，有功功率对于各节点电压影响较大，当分布式光伏出力骤减时，配电网末端节点15、17、29、31处电压出现越下限情况，影响配电网用户的电能质量，且易造成安全隐患。

2)场景1下配电网分布式MPC电压控制整体效果。

考虑配电网光伏、负荷变化易造成配电网电压的频繁波动，施加本文所提方法后，通过分布式光伏和储能进行协同控制，配电网整体电压水平如图9所示。控制接入后电网电压水平维持在0.95 pu以上，可以保证分布式光伏出力剧烈波动下配电网电压稳定。

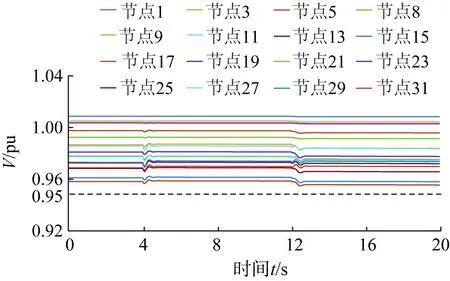
图9 场景1下施加控制后IEEE-33节点拓扑内部分节点电压Fig.9 Voltages of some nodes in IEEE 33-node system after control in case 1

对比无本文方法的情况下，本文所采用方法能够在秒级对电压进行调节，迅速恢复正常运行水平，配电网末端节点15、17、29、31处仍保持在安全下限0.95pu之上，在光伏有功功率出力变化剧烈时仍能保证很好的调压动态性能。

同时，由于无功功率分布不合理会导致配电网运行网损增大和变流器功耗等问题，故在约束条件中对光伏、储能的无功功率予以限制，在上述工况下分布式储能、光伏出力如图10—12所示。

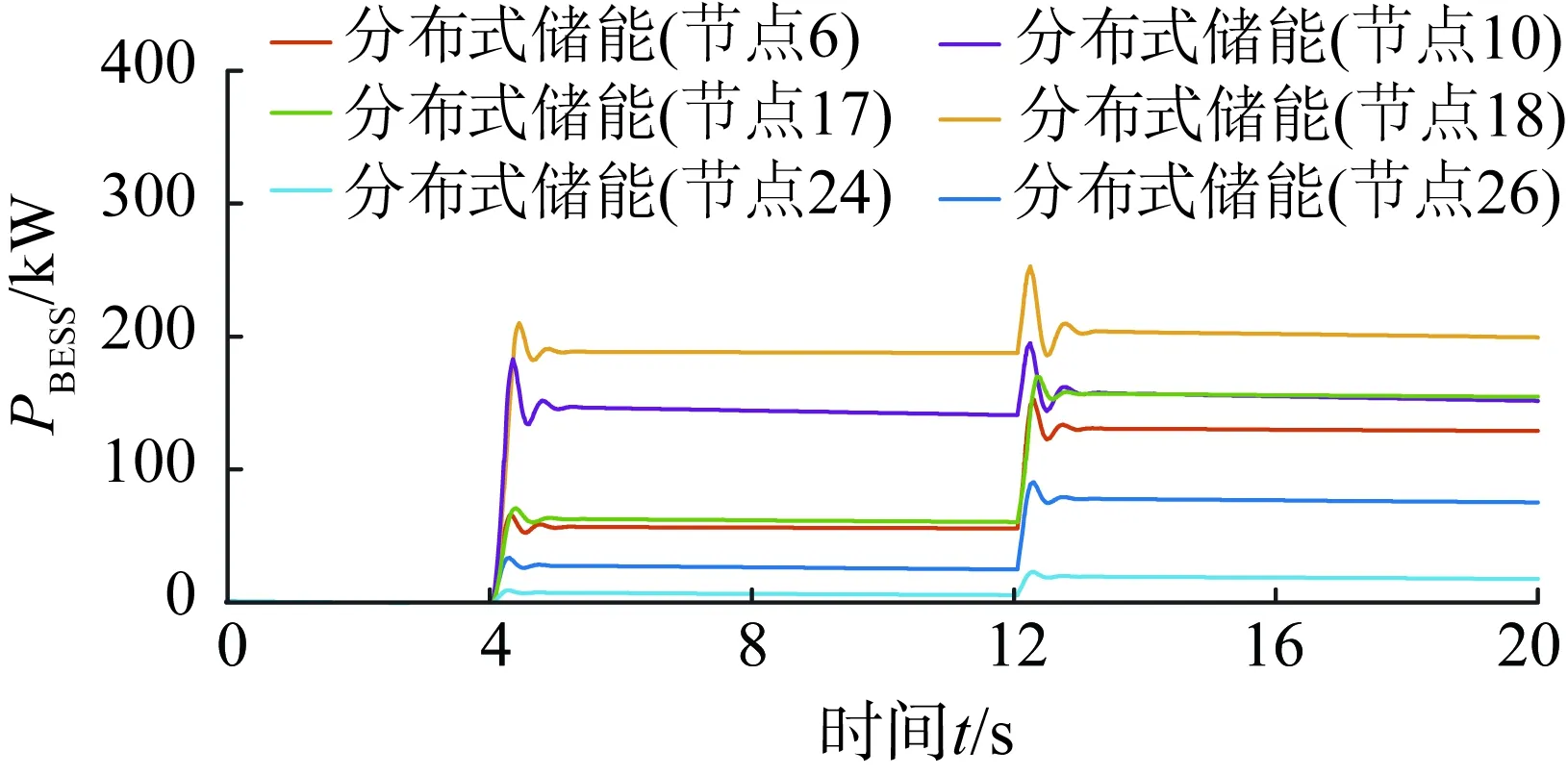
图10 场景1下分布式储能有功功率出力波形Fig.10 Waveform of active power of energy storages in case 1

图11 场景1下分布式储能无功功率出力波形Fig.11 Waveform of reactive power of energy storages in case 1

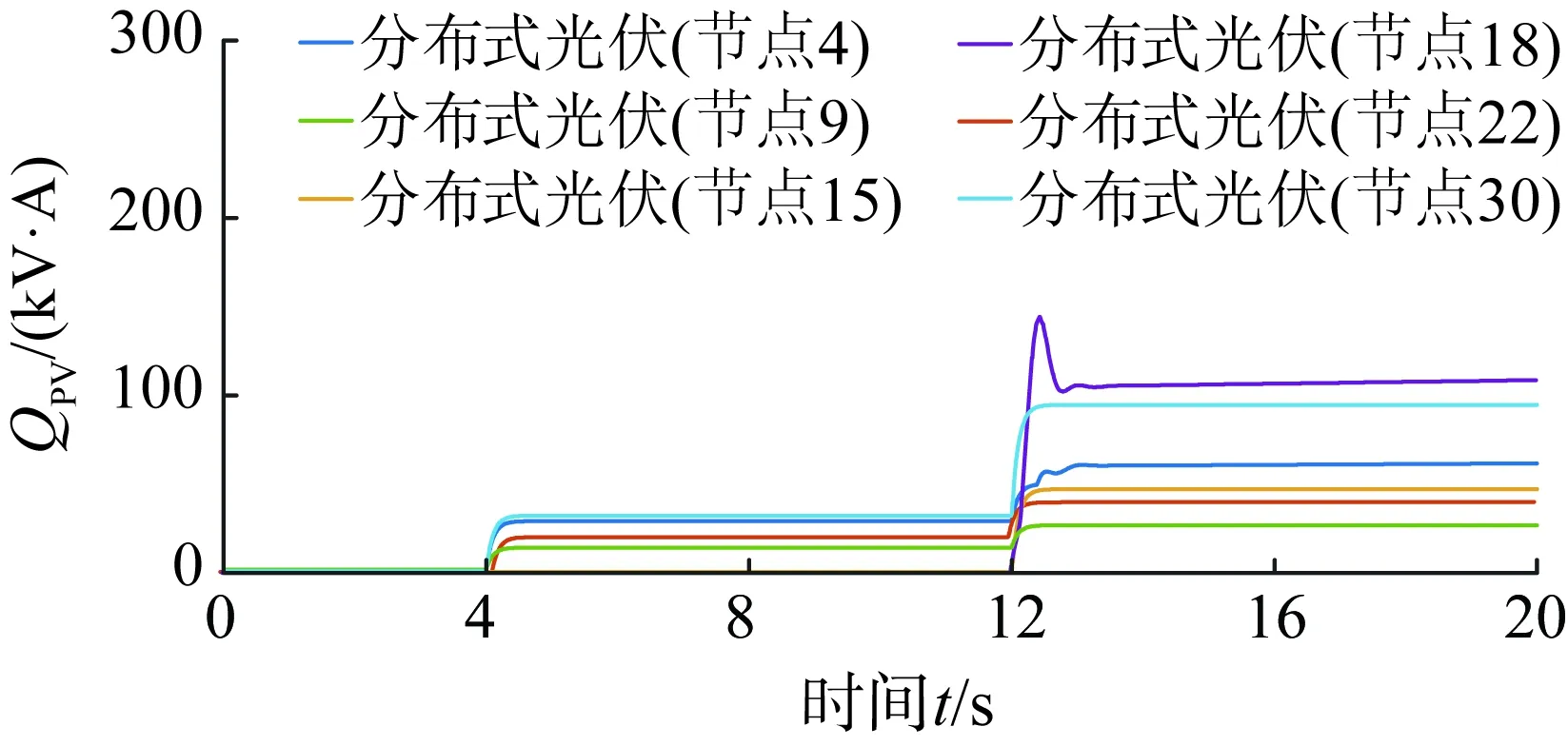
图12 场景1下分布式光伏无功功率出力波形Fig.12 Waveform of reactive power of PVs in case 1

当光伏有功在4 s时发生骤减时，光伏无功出力开始减缓、电压降落。由于光伏并网通常须满足一定的功率因数要求，故其无功功率在有功功率减少时出力十分有限，此时分布式储能有功功率增发弥补光伏骤减的功率缺额，维持电网电压保持原来的水平。在12 s时光伏有功功率进一步降低，分布式储能的有功功率不能完全满足调压需求，则增发一部分无功功率保持电网电压不越限，对电网电压进行快速动态控制。在调压过程中，区域之间能够通过交换功率的方式实现各分区的协调配合，如附录B图B1所示。在此动态过程中各设备的控制量数值变化如附录B图B2、图B3、图B4所示，与各设备的出力趋势相符合。4 s时分区1和3与分区1和2的各自有功功率交互量都存在减少的情况，协同调控多点电压保持正常运行水平。

3.2.2场景2：潮流逆向下光伏出力上升

1)未施加本文控制策略时电压水平。

为进一步体现高渗透率光伏下潮流逆向场景的电压控制效果，本文进一步模拟天气由阴转晴光照强度增大工况，即分布式光伏出力骤增。分布式光伏出力波形如图13所示，即分别在4 s和12 s处设置光伏出力骤增。

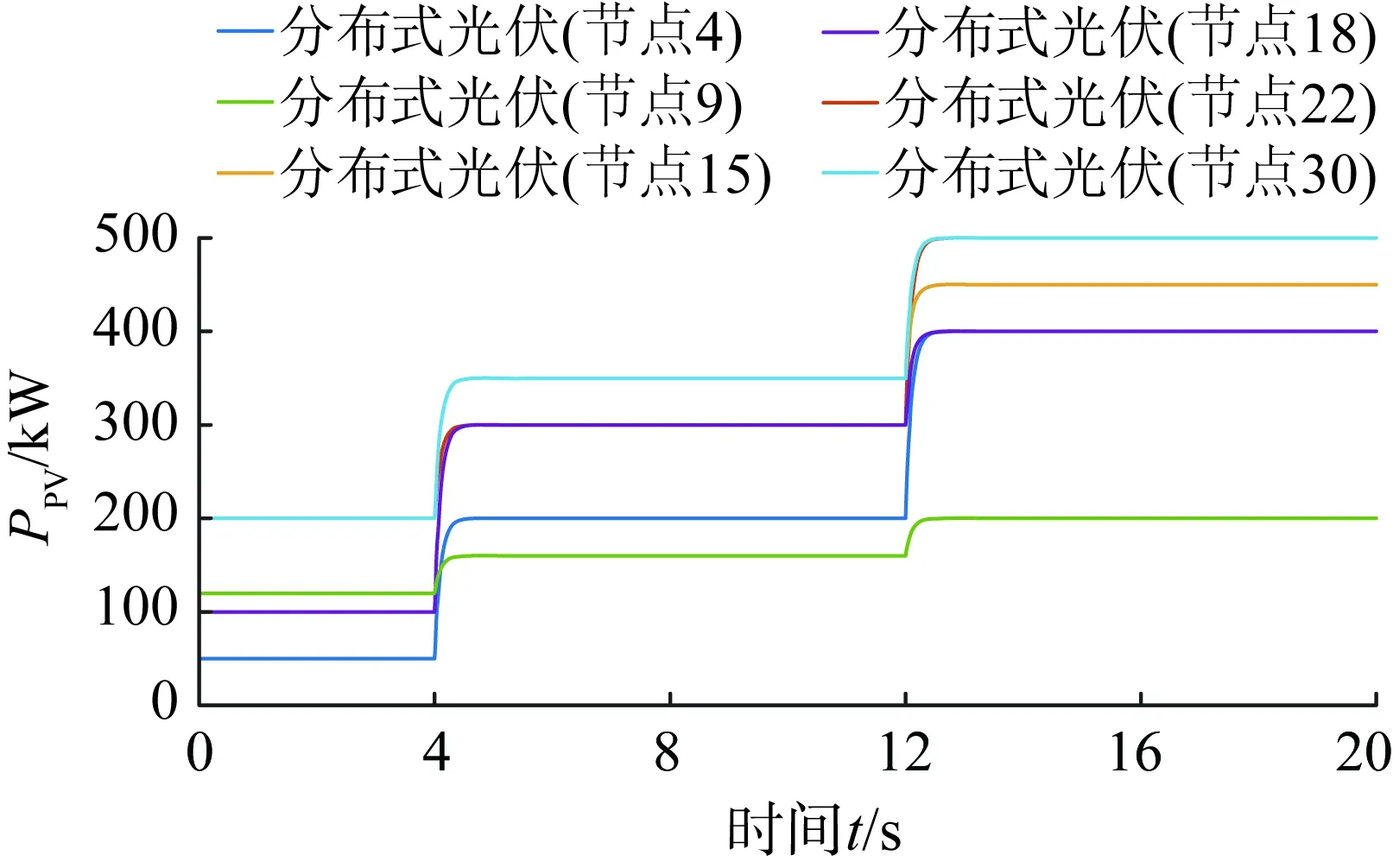
图13 场景2下各分布式光伏有功功率出力波形Fig.13 Active power output of PVs in case 2

场景2下无控制时IEEE-33节点配电网总体电压分布情况如图14所示(仍选取编号为2m+1，m=0、1、…、15的16个节点电压)。配电网末端节点11、13、15、17处电压出现越上限情况，若不进行快速电压恢复控制，会影响配电网安全稳定运行。

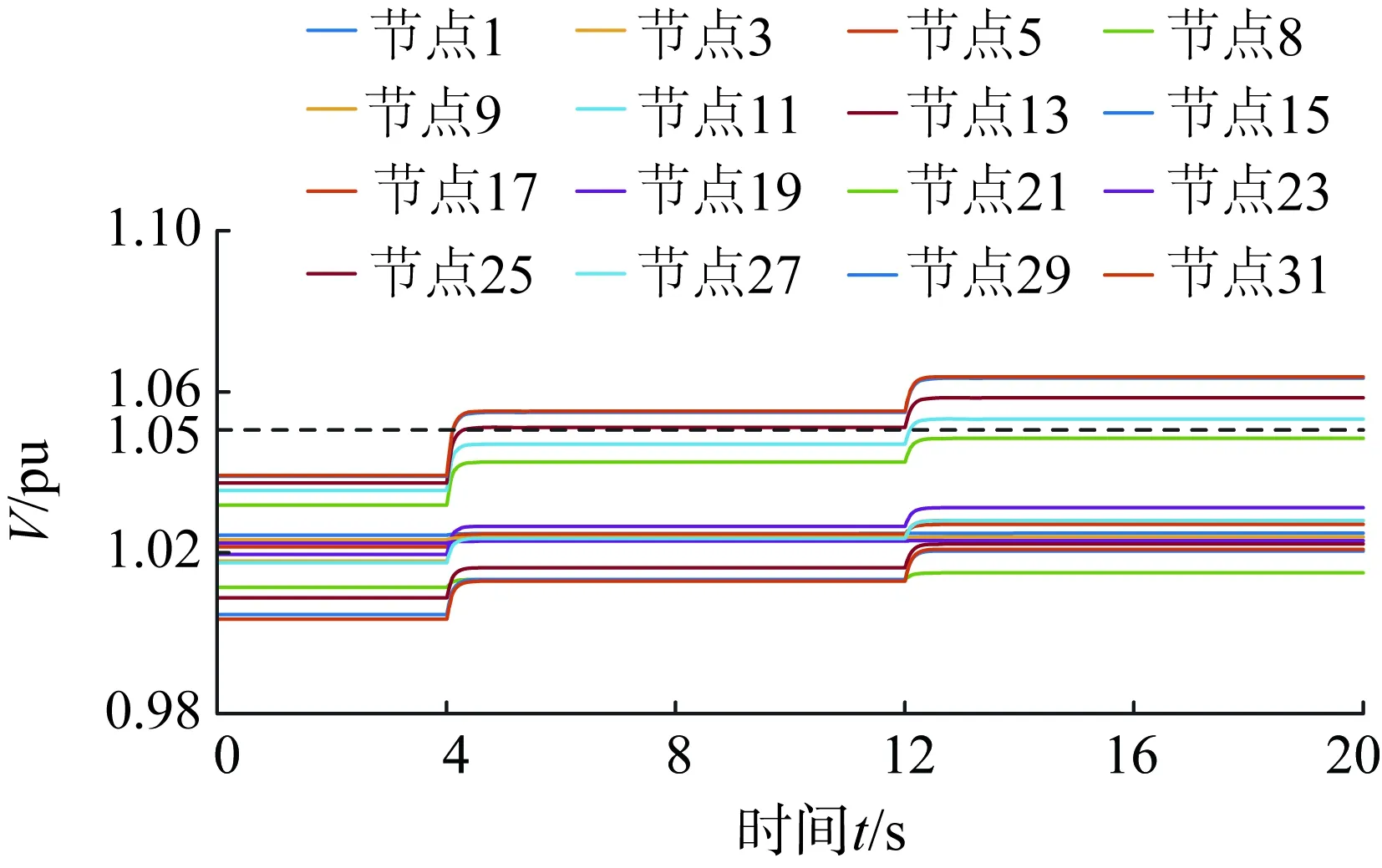
图14 场景2下IEEE-33节点拓扑内部分节点电压Fig.14 Voltages of some nodes in IEEE 33-node system in case 2

2)场景2下配电网分布式MPC电压控制整体效果。

在潮流逆向下时，施加本文所提方法后，通过分布式光伏和分布式储能的有功和无功功率进行协同控制，改善光伏接入后配电网整体电压水平，结果如图15所示。控制接入后电网电压水平维持在1.05pu以下，表明在电压抬升、潮流逆向的场景下，本文方法仍能保持优良的控制效果。

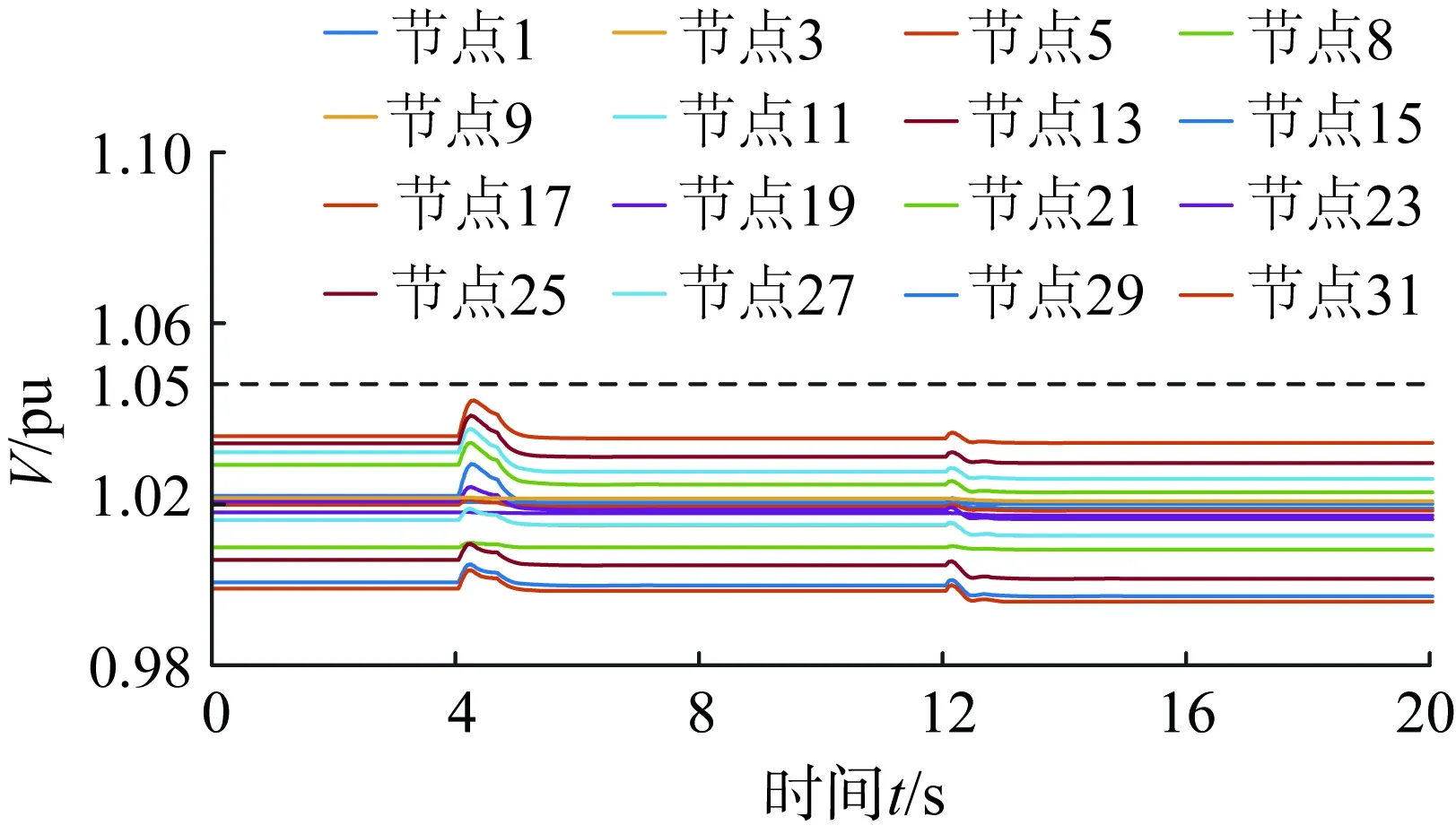
图15 场景2下施加控制后IEEE-33节点拓扑内部分节点电压Fig.15 Voltage of some nodes in IEEE 33-node system after control in case 2

对比无本文方法的情况下，本文所采用方法在潮流发生逆向的情况下仍然能够在秒级对电压进行调节，使电网电压迅速恢复正常运行水平。各调控设备的有功/无功功率保持最优出力方式，其在上述工况下出力分别如图16—18所示。

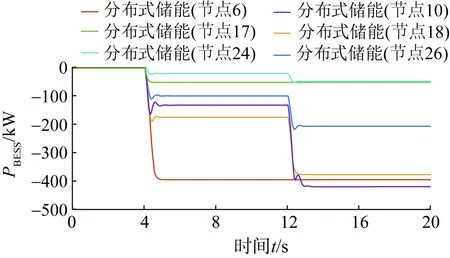
图16 场景2下分布式储能有功功率出力波形Fig.16 Waveform of active power of energy storage in case 2

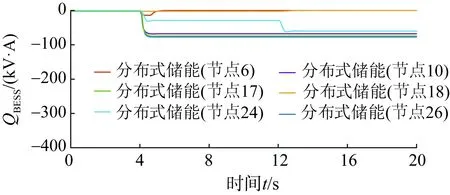
图17 场景2下分布式储能无功功率出力波形Fig.17 Waveform of reactive power of energy storage in case 2

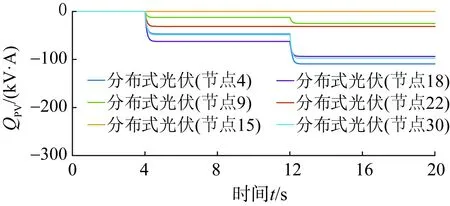
图18 场景2下分布式光伏无功功率出力波形Fig.18 Waveform of reactive power of PVs in case 2

在4 s时，光伏有功功率骤增，光伏无功功率出力减小、电压上升，此时，分布式储能吸收有功功率，弥补光伏骤增引起的电压抬升，从而将电网电压稳定维持在正常水平。

在施加本文方法的调压过程中，各区域之间通过交换功率的方式实现各分区的协调配合,如附录B图B5所示。4 s时分区1和3与分区1和2的各自有功功率交互量都减少，因为不同区域光伏波动引起的电压偏移程度不同，故为保持多节点电压的安全，区域进行协同控制。在12 s时光伏有功功率出力进一步升高，分布式储能(节点6)的有功功率已达到上限无法继续吸收有功功率，不能完全满足调压需求，其他储能则继续增大有功功率吸收以调控电压上升，同时分布式储能的无功也进行相应的调节。在此动态过程中各设备的控制量数值变化如附录B图B6、图B7、图B8所示，与各设备的出力趋势相符合，实现各设备控制指令的准确跟踪。

4 结 论

本文针对含分布式储能有源配电网的电压越限问题，使用了基于分布式模型预测控制的动态调压控制方法，同时针对分布式控制结构中系统解耦的需求,使用了ε分解法，提高了分布式控制的控制性能。在提高配电网电压稳定性的同时，兼顾了光伏和储能设备中存在的实际约束，将光伏自身无功功率容量与储能有机结合起来，实现分布式光伏和储能协同调压的增效优势。仿真结果表明，该方法能够在1～2 s内不断更新分布式光伏和储能的出力，在1～2 s内使发生越限的节点电压重新恢复至安全的稳态运行场景，且此过程中保持光伏功率因数不低于并网要求的0.95，储能的无功功率出力不超过40%变流器额定容量。

需要说明的是，本文未考虑储能变流器的能量转换效率问题与运行经济性问题，若电池长期工作后分布式储能可能由于其状态估计偏差较大而影响控制效果。