面向可靠性评估的两阶段聚类风-光-荷典型场景生成方法
2021-06-09李春燕赵晨宇陈正宇廖庆龙万凌云谢开贵
李春燕, 赵晨宇, 胡 博, 陈正宇, 廖庆龙, 万凌云, 谢开贵
(1. 输配电装备及系统安全与新技术国家重点实验室, 重庆大学, 重庆 400044; 2. 国网重庆市电力公司电力科学研究院, 重庆 404100)
1 引言
“十三五”以来,我国电力行业走上绿色高效转型发展的快速路。截至2020年10月底,全国发电装机21亿kW,其中水电3.7亿kW、风电2.3亿kW、太阳能发电2.3亿kW,预测显示2020年底,全国发电装机将达到21.4亿kW,非化石能源装机占比达到43.7%,比2015年提高8.7%。与传统能源发电相比,风光发电具有无污染、可再生和成本低廉等优势,但受风力和光照等不确定因素影响同时具备波动性和间歇性的典型特征[1]。因此大规模可再生能源并网将对电力系统安全稳定运行带来消极影响。评估含可再生能源的电力系统可靠性对推动电力系统发展意义深远[2]。
目前,国内外对含新能源电力系统的可靠性研究主要基于模拟法(如序贯蒙特卡洛法),通过随机抽样刻画风/光等可再生能源的不确定性,进而计算系统的可靠性指标。文献[3]采用蒙特卡洛法对含风电和光伏的电力系统长期性能进行评估;文献[4]利用基于Well-being模型的蒙特卡洛模拟法分别评估含不同风/光容量配置的发电系统的可靠性,并研究风/光配置容量对可靠性的影响。文献[5]通过模拟风电、光伏出力场景,研究风电、光伏的波动性和负荷的不确定性对电力系统可靠性造成的影响。基于序贯蒙特卡洛模拟的可靠性评估算法可以计及变量的时序相关特性,实现更精确的可靠性指标计算,然而其计算需要大量的场景输入,运算时间较长,计算复杂度较高。随着大数据技术在电力行业的应用与发展,应用场景约简技术实现时间序列聚合,选取较少的典型场景代表原始数据集,可以在简化计算的同时保证计算结果的精度[6]。
现有场景约简技术主要包含K-means聚类、层次聚类法、模糊C均值聚类及谱聚类等。文献[7]基于K-means聚类对风电场历史故障数据进行分析,通过典型场景刻画了故障历史数据特征和类别属性,验证了采用典型场景集代表全数据集的可行性。文献[8]采用最近邻聚类方法对场景进行削减,计算速度快,简便易行。但由于以上算法的原理较为简单,应用于高维数据时存在聚类结果不稳定、平滑原始时序数据的波动特征等弊端。文献[9]根据层次聚类得到各集合的容量,对每个集合的代表场景进行加权,获得能够反映输入数据波动特征的典型场景集。虽然层次聚类可以获得相对稳定的典型场景集,但该算法时间复杂度大,结果依赖合并点和分裂点的选择。
对可靠性评估的典型场景研究目前主要面向元件状态场景和风光荷输入场景。由于风光荷场景具有强不确定性,对风光荷典型场景进行筛选,以典型场景代表全场景可以一定程度上描述其不确定性。考虑风电、光伏出力与负荷之间的相关性具有重要价值。文献[10]提出一种基于改进K-means的典型场景集选取方法,对包括风功率和电力负荷的时序数据集进行聚类分析和场景优选,计及了负荷和风电出力相关性。虽然该算法实现了风-荷联合典型场景选取,但K-means算法处理高维数据时效果有限,而考虑光伏出力会进一步增加数据的维度。
上述研究为典型场景的提取提供了思路,但应用于电力系统可靠性评估时,仍存在两方面问题:①风电、光伏出力具有较强的波动性,且风电具有反调峰特性,风电、光伏和负荷三类数据存在明显的时序相关性,因此需要对风-光-荷高维数据进行场景聚类,同时保留时序特性;②聚类算法会损失极端场景。而在可靠性评估过程中,高负荷水平、低电源出力等极端场景对可靠性评估结果有不可忽视的影响。
基于上述研究,本文提出一种面向可靠性评估的风-光-荷典型场景集选取方法,对包括风电出力、光伏出力和电力负荷的时序数据集进行降维和两阶段聚类,生成考虑风、光、负荷相关性的分层时序典型场景集,对场景集进行优选,得到考虑极端场景对可靠性评估影响的典型场景集。应用于电力系统可靠性评估当中,以传统时序负荷仿真法计算结果作为参照,对比分析算法的计算速度及各项指标误差。
2 问题描述和研究思路
为实现面向可靠性评估的风-光-荷典型场景生成,目前主要存在以下3个问题:
(1)为使聚类结果适用于可靠性评估,需要选择合适的曲线特征对风-光-荷场景进行聚类。
(2)为保留风-光-荷场景的风、光、负荷相关性及时序特征,需要对高维数据进行聚类,现有聚类算法对高维数据直接聚类效果并不理想,需要采用多次聚类和降维算法改进聚类算法。
(3)现有研究多采用聚类中心作为典型场景,由于聚类算法的特性,极端场景一般不作为聚类中心出现,但电力系统可靠性评估对负荷水平较高的场景非常敏感,忽略极端场景会明显影响评估结果的精度。因此需要计及极端场景的典型场景优选方法。
为解决以上问题,本文基于DBSCAN和K-means聚类提出了一种适用于含新能源电力系统可靠性评估的典型场景生成的两阶段聚类方法。首先,选用净负荷持续曲线作为风-光-荷场景特征,基于分层抽样的思想,采用DBSCAN聚类算法将风-光-荷场景分层;然后采用SAX降维算法对原始风-光-荷时序曲线进行降维,使用K-means聚类算法对每层曲线进行分别聚类,得到保留时序特征的风-光-荷场景聚类结果。最后依据基于核密度估计发电系统状态的可靠性评估结果指标对各层曲线集进行场景优选,生成计及极端场景影响的时序风-光-荷典型场景集,应用于含新能源的电力系统可靠性评估,具体流程如图1所示。

图1 基于分层抽样的典型场景生成方法Fig.1 Stratified sampling based typical scenario generation method
3 基于DBSCAN和改进K-means的风-光-荷典型场景生成
运用典型场景进行可靠性评估可以大大削减计算量,提高计算效率。典型场景生成的关键点和难点在于如何对大量原始场景进行削减,实现减小计算负担的同时保证削减后的场景集尽可能逼近原始场景。本文目的是寻找适用于可靠性评估的典型场景,因此需要对原始场景中可靠性评估相关特征进行发掘,利用特征筛选典型场景。
3.1 基于DBSCAN分层的日净负荷持续曲线分类
分层抽样法是将总体单位按其属性特征分成若干层,在层中按一定比例随机抽取样本单位。本方法通过划类分层,增大了各层级中单位间的共同性,使得样本代表性较好,抽样误差较小。因此更适用于总体情况复杂,各单位之间差异较大,单位较多的情况。
电力系统的失负荷量与失负荷概率与系统某时刻的净负荷水平有着不可分割的关系。净负荷指某一时刻系统的用电负荷与同时刻新能源出力差值,由于某一时刻可靠性评估指标与该时刻负荷水平直接相关,净负荷值越大,失负荷概率越高,切负荷量也越大。为舍弃负荷曲线冗余特征,提高计算效率,本文首先基于密度对日净负荷持续曲线进行聚类,得到依据负荷水平的负荷样本分层,从而确定负荷输入的优先级,约简对可靠性评估指标影响较小的场景,提高计算效率。
在将每天各时刻的净负荷按照从大到小的顺序进行重排形成日净负荷持续曲线后,本文引入并改进基于密度的有噪应用中的空间聚类算法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)算法对日净负荷持续曲线进行聚类。DBSCAN算法是一种基于密度的聚类算法。此算法不需要预先指定簇的个数,而是根据样本数据点分布密度进行聚类,因此可以识别数据量稀少的离群值,应用在场景削减中可以保留极端场景。
DBSCAN算法需要设定两个重要参数: DB领域半径值(Epsilon,Eps)和领域密度阈值(Minimum Points,MinPts)。Eps表示个体之间距离临界值,MinPts表示临界距离半径中个体数量的临界值。传统DBSCAN算法中Eps和MinPts由经验设置再根据聚类结果进行调整,存在较大的盲目性。本文采用绘制k-距离曲线方法[13],选取k-距离曲线图明显拐点位置为聚类参数确定Eps。MinPts的选取遵从原则:
(1)
式中,si为点i的Eps领域内个体的数量;Np为Eps领域个数。对于样本数据集D=(X1,X2, …,Xm),其中X为风-光-负荷原始场景数据,m为原始场景个数,DBSCAN算法流程如图2所示。
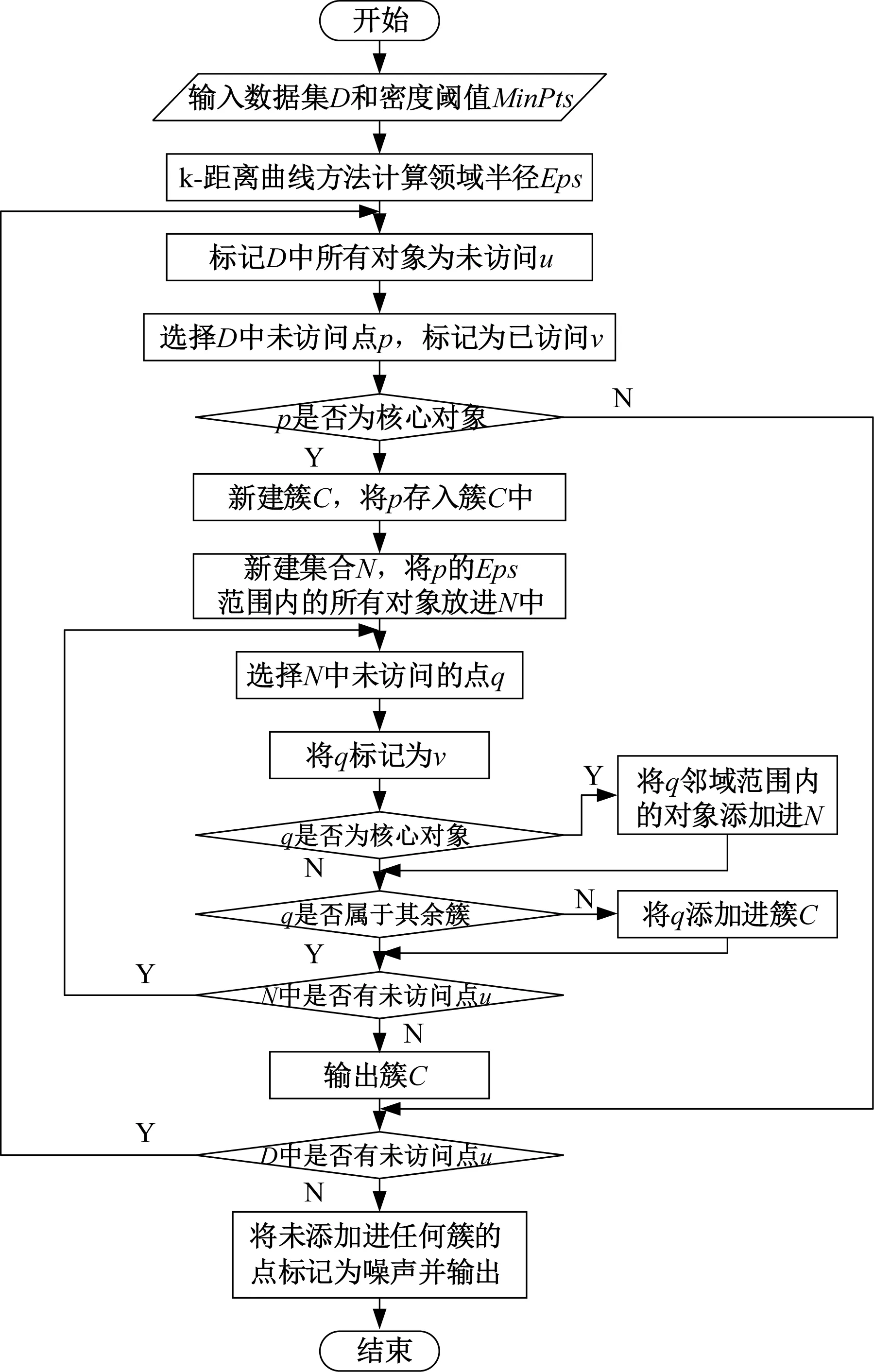
图2 DBSCAN算法流程图Fig.2 Flow chart of DBSCAN algorithm
利用上述算法对日净负荷持续曲线进行聚类实现对风-光-荷原始场景集D的分层,得到分层场景集{D1,D2,...,Ds},所得不同场景集在峰值负荷大小及负荷分布上有明显分级。
3.2 基于优化SAX的K-means聚类算法
基于分层场景集{D1,D2,...,Ds},本文采用改进的K-means聚类算法对每一层风-光-荷场景进行削减,得到保留时序特征的分层典型场景集。
K-means聚类算法是一种简单、高效的无监督聚类分析算法。随机选取空间中k个点为中心进行聚类,计算每个对象与k个点对最靠近聚类中心的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至所有数据点到其所在类中心的距离和达到最小值。K-means聚类使用方法简便,且具有较好的计算效率,但该算法对高维数据聚类效果不理想。
为了实现对高维海量的风电、光伏和负荷数据聚类,同时保留其时序特征,需要对数据进行降维处理。符号聚合近似(Symbolic Aggregate Approximation,SAX)是一种将连续时间序列转化为离散字符变量的算法,可以有效地降维、降噪,且结果更为直观,具有处理速度快,便于状态分析等优势,在异常数据检测,模式识别等领域应用广泛[11,12]。本文主要介绍SAX参数优化的相关部分。

图3 风电出力曲线的SAX表达Fig.3 SAX expression of WP curve
(2)
(3)
式中,β为字符断点值;L为负荷曲线X转化后的离散状态表示。
本文从准确度A、信息量E、化简率R三个角度,综合考虑负荷曲线SAX表达的效果。其含义如下:准确度A反映分段后的风-光-荷曲线表征原曲线的能力;信息量E采用信息熵衡量分段后的曲线还原原曲线的能力,信息熵越小,则通过现有信息进行预测时的确定性越大,其所含信息量越大;化简率R则表征原始曲线的被压缩程度。通过三个指标对算法效果进行评估,达到综合效果最优,即得到最优的风-光-荷曲线降维表达。
将风-光-荷曲线SAX表达的优化过程转化为多目标优化问题,其中目标函数为:
Objective=max(A,E,R)
(4)
其中
(5)
(6)
(7)
2≤l≤lm
(8)
2≤w≤wm
(9)
针对多目标整数规划问题,相较其他算法,粒子群算法更为简单有效,具有精度高、收敛快等优势[14]。本文采用基于模拟退火的粒子群算法,其在搜索过程中具有概率突跳的能力,能够有效地避免搜索过程陷入局部极小解的情形[15]。
改进后的参数优化算法流程主要有以下7个步骤:
Step 1:输入粒子数目N,学习因子c1,c2,退火常数λ,最大迭代次数M,初始温度T0;
Step 2:随机初始化种群位置和速度;
Step 3:利用目标函数计算每个粒子适应度并记录最优个体Pg;
Step 4:将T赋值为初始温度T0,i赋值为1;

Step 6:更新粒子位置和速度,计算新目标值并更新各粒子适应度值;
Step 7:判断i是否大于等于M或满足阈值,若符合条件,结束算法;若不符合,i自增1后返回Step 5,直到i满足退出条件。
其中粒子数N=8。通过随机初始化生成代表分段数和字符数的粒子集后,根据目标函数和自变量约束进行优化。在退火过程中不仅接受较优的解,也以一定的概率接受较差的解,同时这种概率受到温度参数的控制。
3.3 基于核密度估计的聚类中心典型场景筛选
3.2节所述算法所得聚类中心为数据分布中心,为考虑可靠性评估相关因素,需要依据场景对应的可靠性指标在聚类所得场景集中进行典型场景筛选。
本文基于核密度估计参数估计建立元件故障模型[16]拟合发电机停运容量分布,对IEEE RTS-79标准测试系统进行发电系统快速可靠性评估得到第i类对应的日平均停电时间期望为:
(10)
式中,LOLEij为第i类第j天对应的日停电时间期望;ni为第i类所包含风-光-荷联合曲线条数。
|LOLEi,LOLEij′|=min|LOLEi,LOLEij|
(11)
则第i类场景集典型场景选取j′作为此类的典型场景输入可靠性评估算法。
4 典型场景生成算法总体流程
本文首先选取DBSCAN聚类算法对日净负荷持续曲线进行聚类,能够实现对大量数据的快速初步聚类,得到不同净负荷水平的场景集。然后采用改进K-means聚类算法,以对初步聚类结果进行高质量的二次聚类,同时保留风-光-荷出力的时序特征,最后对聚类结果进行筛选,得到适用于可靠性评估的风-光-荷典型场景集。整体算法流程如图4所示。

图4 基于DBSCAN和改进K-means 的两阶段聚类流程图Fig.4 Flowchart of two-stage clustering based on DBSCAN and improved K-means
在聚类评价中采用DB (Davies-Bouldin) 指标作为算法评价指标,DB指标计算公式如式(12)所示,其值越小,则类间的相似度越低,类中相似度越高,聚类效果越好。
(12)
式中,c为聚类数;Wi为i类内数据点到聚类中心Cj的平均距离;Wj为j类内数据点到聚类中心Cj的平均距离;Cij为聚类中心i与j之间的距离。
5 算例分析
5.1 算例介绍
本文算例采用的平台为1.7 GHz CPU和8 GB内存的计算机,使用MATLAB 2014a进行算法仿真。为减少数据异常及缺失对数据分布的影响,保证聚类结果的正确性,本文已去除全零负荷并采用分段多项式拟合对曲线进行平滑处理,详见文献[17]。
5.2 算法性能测试结果
为测试算法的高效性,本文采用IEEE 8 736 h标准负荷数据[18],共计364条负荷曲线进行聚类,对以下4种算法进行对比:
方法1:未改进的K-means聚类算法;
方法2:AP聚类算法;
方法3:文献[13]中自FCM算法;
方法4:本文所述DBSCAN和K-means两阶段聚类算法。
为了算法的统一性,方法1,2,3均为在Matlab自带K-means算法的基础上进行实现。由于传统K-means算法需要事先输入聚类数目,为了方便比较,令方法1和方法3的聚类数c=15。方法4两阶段聚类最终聚类数为15。对上述四种算法的DB值及总计算时间分别进行计算,得到结果如表1所示。

表1 算法结果对比Tab.1 Algorithm performance comparison
方法1由于算法复杂度低,计算时间最短,然而传统K-means算法在数据迭代过程中收敛慢,在本文数据下,达到聚类迭代最大次数时,聚类中心尚未达到稳定,导致K-means算法的DB指标值高于其他算法;方法2中AP聚类通过相似度矩阵进行聚类,具有自适应的聚类数, DB指标优于传统K-means算法,但此类算法复杂度较高,所需总计算时间明显长于其他算法。方法3所需计算时间短,DB指标更优,算法表现上较好。方法4改进之后由于增加了一次聚类及降维过程,总计算时间有一定增长,但仍小于方法2,且DB指标明显优于其他算法。结合DB指标和计算时间看,方法3和方法4较有优势。
为测试算法的有效性,本文将以上四种聚类算法的结果作为典型场景输入IEEE RTS-79标准系统中,利用枚举法进行发电系统可靠性评估,所得结果如表2所示。

表2 基于状态枚举法的发电系统可靠性评估结果Tab.2 Reliability evaluation result of power generation system based on enumeration method
表2中,EENS指标(Expected Energy Not Supplied)表示测试系统运行一年的失负荷量。由表2可知,方法2和方法3所得EENS指标与全部场景输入所得差值非常大,方法1差值较小,且差值随聚类数的增大逐渐减小,方法4差值最小,原因主要是:①由于可靠性评估的失负荷状态主要发生在负荷水平较高的情况下,而在聚类过程中,负荷水平较高的场景往往是类别中的边缘点,通常不能作为聚类中心,因此以聚类中心作为典型场景评估所得年失负荷量会明显偏低;②方法1、3、4都需要人为指定聚类数目,聚类数的多少会明显影响可靠性评估的结果。
另外,方法3算法对满足正态分布的数据聚类效果较好,但由于季节、天气等因素影响,用电数据并不呈正态分布,因此方法3用于用电数据聚类效果一般。而方法4算法简单,可以通过经验结合枚举法找出最优聚类数,且聚类结果较好。结合计算效率和有效性,方法4较有优势。
根据比较可以看出,DBSCAN和改进K-means两阶段聚类算法在实际应用中,能够获得较高的聚类效率和较好的应用效果。
5.3 IEEE标准系统测试结果
数据集来自比利时某电力公司官方网站2017~2018年负荷、风力发电数据及某光伏电站一年光伏发电上网数据[19],选取负荷曲线,风电出力曲线及光伏出力曲线各365条,并对有效曲线进行了离差归一化处理。图5给出了数据集对应净负荷持续曲线DBSCAN聚类后的聚类中心。

图5 净负荷持续曲线聚类结果Fig.5 Result of net load duration curve clustering
从图5可见,类1到类5的按峰值负荷大小有明显阶梯状分层,类2最大,类5最小。类1,2,3场景峰值负荷较大,用电峰谷差也较为明显,类4,5场景负荷水平较低,用电情况较为稳定。以上结果表明采用净负荷持续曲线的DBSCAN聚类可以对风-光-荷场景实现较好的分层效果。
将各层聚类中心代入IEEE RBTS-6测试系统采用枚举法进行发电系统可靠性评估计算,得到可靠性指标如表3所示。
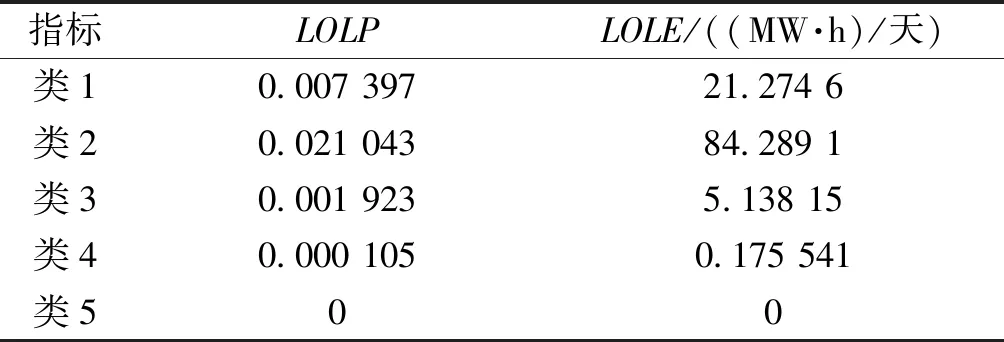
表3 各层聚类中心可靠性评估结果Tab.3 Reliability indices of clustering centers
表3中,LOLP指标(Loss of Load Probability)为测试系统一天的失负荷概率,LOLE指标(Loss of Load Expectation)为测试系统一天的失负荷量。由表3可知,类2聚类中心作为输入计算所得失负荷量最大,类5聚类中心计算所得失负荷量最小。净负荷持续曲线峰值越大,计算所得失负荷量越大。由此可见,净负荷大小与失负荷量呈正相关,本文对净负荷持续曲线分层对后续可靠性评估计算正确有效。
表3中分类结果的原始数据集即为根据净负荷持续曲线分层后的场景集,利用改进K-means分别对每一层进行聚类,经过多次试验,本文设k=3。聚类结果为5层,每层3类,共15类场景集。对所得场景集进行筛选,用基于核密度估计的可靠性评估算法在每一类中筛选出最终适用于可靠性评估的典型场景,舍弃部分相似场景后结果如图6所示,各典型场景出现概率如表4所示。
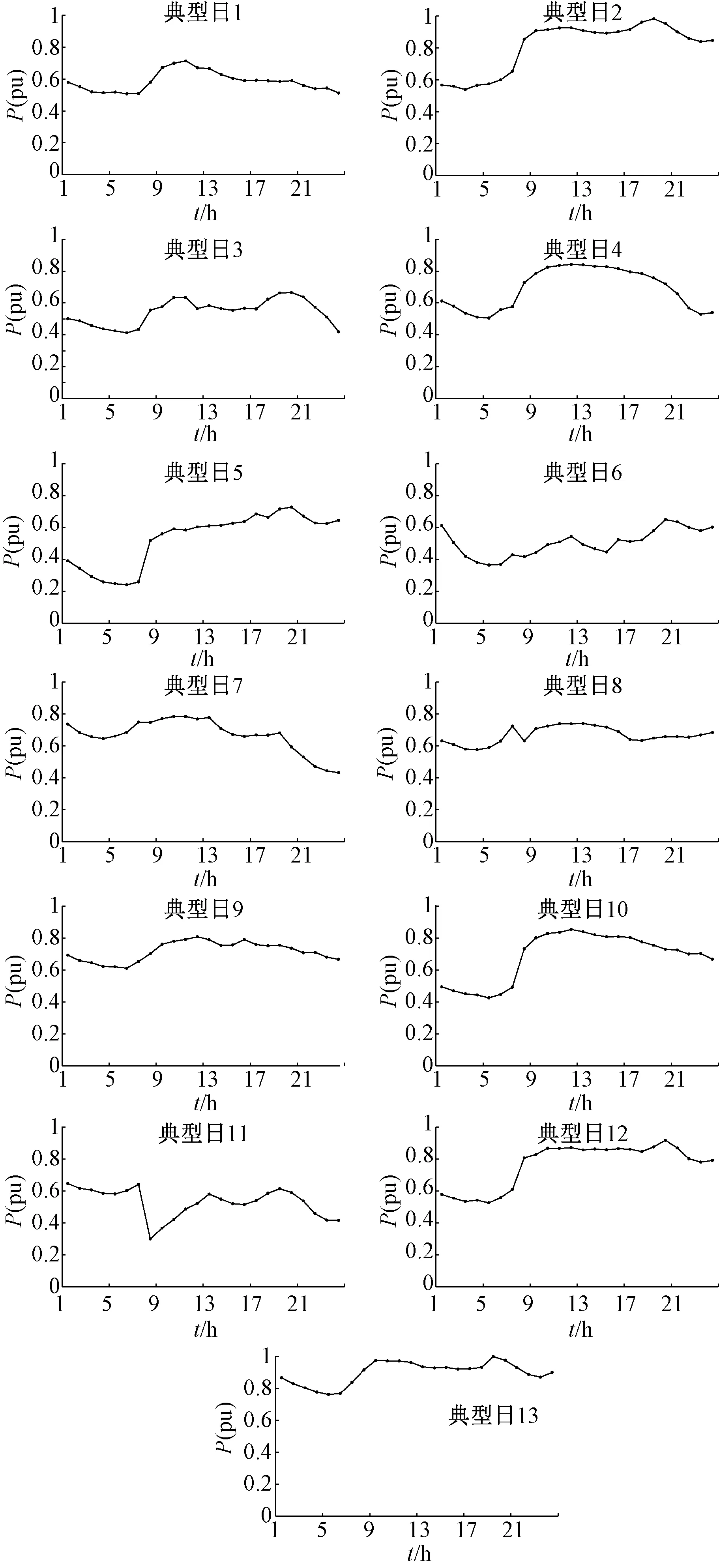
图6 DBSCAN和K-means两阶段聚类后筛选所得典型日Fig.6 Typical scenarios from DBSCAN and K-means two-stage clustering

表4 各典型场景对应概率Tab.4 Probability of typical scenarios
本文对IEEERTS-79标准测试系统进行改进,在节点7添加风电出力输入,节点22添加光伏出力输入,该系统接线图如附图1所示。改进后测试系统上采用图6中所示的时序典型场景及各场景对应概率,依概率进行基于序贯蒙特卡洛抽样的可靠性评估,得到的可靠性指标与输入一年365天风-光-荷数据对比如表5所示。

附图1 IEEERTS-79标准测试系统接线图 App.Fig.1 Diagram of IEEERTS-79 reliability test system

表5 典型场景与全场景输入的序贯蒙特 卡洛仿真结果对比Tab.5 Comparison of sequential Monte Carlo simulation results using typical scenarios and full scenarios
表5中,LOLF指标(Loss of Load Frequency)为电力不足频率,即单位时间内停电的次数。从表5可见,典型场景输入计算所得EENS指标对比全场景输入误差率为2.82%,较其他聚类算法所得典型场景输入误差较小,误差不为零的原因是聚类算法原理导致聚类过程中可能会丢失对可靠性评估指标影响较大的边缘点,采用本文算法选取典型场景可以一定程度减少此类误差,但不能完全消除。而运用典型场景进行可靠性评估较原方法计算时间缩短60%,显著提升了计算效率。由此可见,利用本文所提出的DBSCAN和改进K-means聚类典型场景生成方法所得的时序典型场景适用于可靠性评估计算,兼具高效性与准确性。
6 结论
本文提出了一种适用于含可再生能源电力系统可靠性评估的DBSCAN和改进K-means两阶段聚类典型场景生成方法。首先基于分层抽样的思想,采用密度聚类将净负荷持续曲线分层,然后采用SAX算法改进K-means聚类算法对风-光-荷原始曲线进行降维聚类,依据核密度估计可靠性评估LOLE指标对各层曲线集进行场景筛选,最终生成保留时序特征的风-光-荷典型场景。
该算法在保证聚类算法效率的同时,对高维数据聚类效果良好。最终所得时序风-光-荷典型场景用于电力系统序贯蒙特卡洛可靠性评估,显著提升算法效率的同时保证了可靠性评估的准确性。
场景约简技术作为一种稳定、高效的简化计算方法,在可靠性评估中具有很大的研究价值。下一步研究可以尝试关注极端场景,在聚类过程中保留边界点,细化高负荷水平场景的分类,从而进一步减小可靠性评估误差。
附录
