一类具有时滞和Holling III型功能反应的捕食系统的定性分析
2021-06-09叶丽霞兰德新李燕云
叶丽霞,兰德新,李燕云
(武夷学院 数学与计算机学院,福建 武夷山 354300)
在种群生态学中,捕食者—食饵系统之间的关系,一直以来都是生物数学研究的重点,它对于生物界种群的死亡和发展有着重要的影响。功能性反应函数对于捕食者—食饵系统有着重要的意义,它能够确切地表现出捕食者的捕食能力。Holling[1]通过实验,得出了不同物种的三种不同的功能反应函数。文献[2-5]对Holling II 、Holling III型的捕食者—食饵系统的正周期解的存在性、正平衡点的稳定性等动力性行为建立了相应的研究成果。在生物系统中,种群的捕捞或放养在极短时间内不会对种群密度造成极大的变化,即表现为时滞现象,因此,时滞对生物的演化具有重要的影响。研究表明,建立具有时滞的生物模型具有非常重要的应用价值[6-13]。

1 基本概念
研究Rn中的微分方程组
(1)
定义1[9]若∀ε>0,∃δ>0(δ一般与t0和ε有关),使当任一x0满足‖x0‖≤δ时,式(1)描述的系统由初始条件x(t0)=x0确定的解x(t),对一切t≥t0均有‖x(t)‖<ε,则称系统的零解x=0为稳定的。
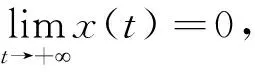
定义3[9]若式(1)描述系统的零解x=0为渐进稳定的,且吸引域是Rn,则系统为全局渐进稳定的。
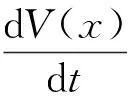
2 主要结论
本文考虑的具有时滞和Holling III型功能反应的捕食系统被描述如下:
(2)
其中x(t)表示t时刻食饵的密度;y(t)表示t时刻捕食者的密度;r为食饵固有增长率;q为捕食者死亡率;a为食饵中间作用系数;b为捕食者中间作用的系数;m为半捕捉饱和常数;τ为捕食者从幼年到具备捕食能力所需要的成长时间;r、a、q、b皆为正数。
2.1 持续性生存
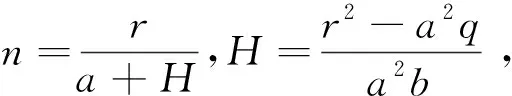
证明由式(2)可得x′(t)≤x(t)[r-ax(t)],由比较原理知:
(3)
同理可得:
(4)
(5)
(6)
由条件(i)~(ii)知,n,N,h,H均存在,且全部大于0,则该系统是持续性生存。
2.2 正平衡点的存在性
定理2设式(2)描述的系统中的系数r,a,m,q,b为正数,若该系统满足(1-qm)r-abq>0,r2-a2q>0时,则该系统存在正平衡点。
证明设式(2)的平衡点为E*(x*(t),y*(t)),则
(7)
由式(7)可得:
(8)
则有
-abm2x*5(t)+brm2x*4(t)+(qm-2abm-1)x*3(t)+
2brmx*2(t)+(q-a)bx*(t)+br=0.
令
由于r,a,m,q,b皆为正数,则有:
则函数f(x*(t))在(0,+∞)穿过x轴,即关于x*(t)的方程在(0,+∞)有解,即系统(2)存在x*(t)>0的解。
下面证明系统(2)存在解y*(t)>0.
由定理2的已知条件(1-qm)r-bq(a+H)>0,r2-a2q>0及r,a,m,q,b为正数,可得(1-qm)>0,则式(8)可化为
故系统(2)存在正平衡点。
2.3 全局渐进稳定
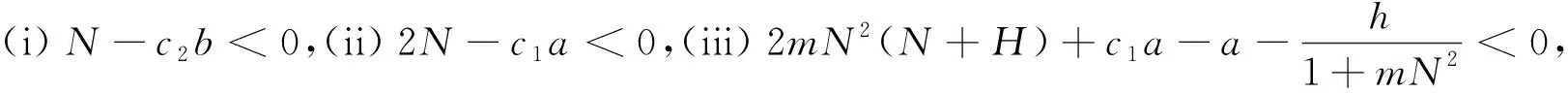
证明构造Lyapunov函数如下:
其中c1,c2为大于零的常数,V(t)为定正函数。
将V(t)函数沿着式(2)对t求导数
c1a[|x(t)-x*(t)|-|x(t-τ)-x*(t-τ)|]+c2b[|y(t)-y*(t)|-|y(t-τ)-y*(t-τ)|]+
c1a[|x(t)-x*(t)|-|x(t-τ)-x*(t-τ)|]+c2b[|y(t)-y*(t)|-|y(t-τ)-y*(t-τ)|]=
{[mx*2(t-τ)+mx*(t)y(t-τ)][x(t)+x*(t)]-(1-c1)a}|x(t)-x*(t)|-
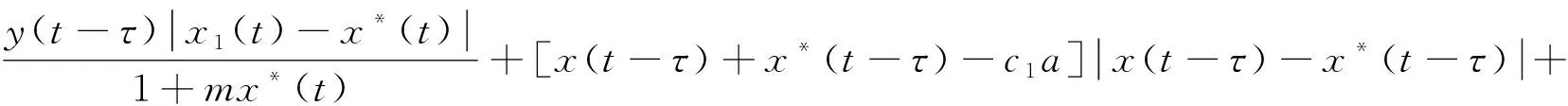
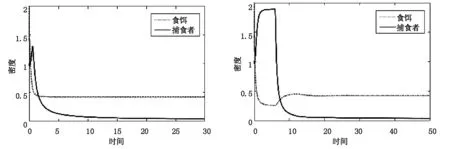
由于0 取系统(2)的初始值为(2,1),即食饵的密度为2,捕食者的密度为1,r=1,a=2,m=0.5,q=0.1,b=2,用Matlab对系统(2)在τ=0.55和τ=6进行仿真,结果如图1~2所示。 图1 τ=0.55捕食者和食饵的密度函数图像 图2 τ=6捕食者和食饵的密度函数图像 可以看出,图2趋近稳定的速度比图1 更慢,表明时滞因素能够延迟系统达到稳定,对系统的稳定性有重要影响。 本文基于实际应用背景,考虑捕食者从幼年到具备捕食能力需要成长时间,对功能反应函数中的捕食者y(t)和食饵x(t)加入时滞效应,研究了一类具有时滞和Holling III型功能反应的捕食者-食饵系统,分析了该系统的持续性生存、正平衡点的存在性和全局渐进稳定。定理1和定理2分别给出该系统持续性生存和正平衡点存在的一个充分条件,定理3给出该系统达到全局渐进稳定的一个判别定理。最后,通过对系统(2)选取合理参数,借助Matlab软件作图,具体描述系统在不同时滞因素下捕食者和食饵的密度随时间变化的情况图,结果表明时滞因素能够延迟系统达到稳定,对系统稳定具有重要的影响。
3 数值仿真
4 结束语
