外热式回转窑传热过程计算流体力学模拟与强化

谭心舜,仲 华,郑世清,毕荣山

(青岛科技大学a.计算机与化工研究所;b.化工学院,山东 青岛266042)

据统计,全世界每年产生废旧轮胎约1 700万t[1]。由于轮胎极难降解,容易燃烧且热值很高,是一种危险固体废弃物,对其进行有效处理具有重要意义[2]。热解作为废旧轮胎处理方法之一,可以生成热解气、热解油和活性炭等有用产品[3-5],因此被认为是最有前景的一种废旧轮胎综合处理方式[6]。回转窑因结构简单、技术成熟、投资低,广泛用于热解过程中[7]。典型的工业回转窑没有折流板,一般用于间歇过程,但存在操作周期长、传热效率低、容易造成热解产物二次反应的缺点。为了克服这些缺点,很多学者进行了研究:BABLER等[8]建立了用于生物质热解过程的外热式回转窑数值模型,探究了传热过程和颗粒流之间的强烈相互作用规律,但忽略了烟气和窑壁之间的传热过程;BONGO等[9]在中试规模外热式的回转窑实验数据的基础上,提出了基于维度分析的系数模型,获得了外热式加热回转窑壁面-固体之间的传热系数,但忽略了电阻到窑壁传热过程;吴静等[10]预测了大颗粒低填充率外热式回转窑内壁与颗粒间的传热过程,但同样没有考虑热源到窑壁之间的传热。SCHAFFER等[11]研究了棉花秸秆在回转窑中的热解过程,但没有深入探究回转窑传热过程的影响;IOVANE等[12]利用实验数据验证了外热式回转窑内棕榈壳蒸汽气化过程,认为蒸汽比例对产气量具有重要影响。以上研究只是针对典型回转窑的热解相关过程进行研究,并没有对设备进行改进。LAM等[13]利用计算流体动力学(CFD)模拟在典型外热式回转窑热解的基础上,提出了添加窑内折流板可以提高间接燃烧窑的热效率,但他没有考虑窑床运动和外部热烟气运动的影响;YOUNG等[14]使用氧化铝球作为填料的回转窑反应器实现了牛皮纸木质素的连续热解,与传统的固定床反应器热解相比,显著提高了油产品的质量并使炭团聚最小化。以上研究针对的都是外热式回转窑窑壁与窑内的传热过程,并未涉及到由热源到窑壁的传热过程。外热式回转窑的传热过程类似于管壳式换热器,壳程结构对整体传热过程同样具有重要的影响[15]。EMAD等[16]通过对比实验研究了壳程4种不同折流板结构对换热过程的影响,结果显示混合折流板的增加可以大幅改善回转窑的换热性能;ANAS等[17]对带有螺旋折流环的双管换热器进行了数值模拟,结果同样显示螺旋折流环增强了传热性能。由此可见,折流元件的加入对加强传热具有很大的作用。本工作建立了典型废旧轮胎热解用回转窑外加热过程的CFD模型,通过分析其内部流场和温度场分布,提出了适合的添加折流板以强化传热的方案,并对增加折流板前后的传热效率进行了比较。

1 计算模型

1.1 湍流模型

1.1.1 标准k-ε模型

标准k-ε模型[18-20]具有稳健性,经济性和准确性的优点,因而在工业回转窑中广泛使用。标准kε模型方程如下:

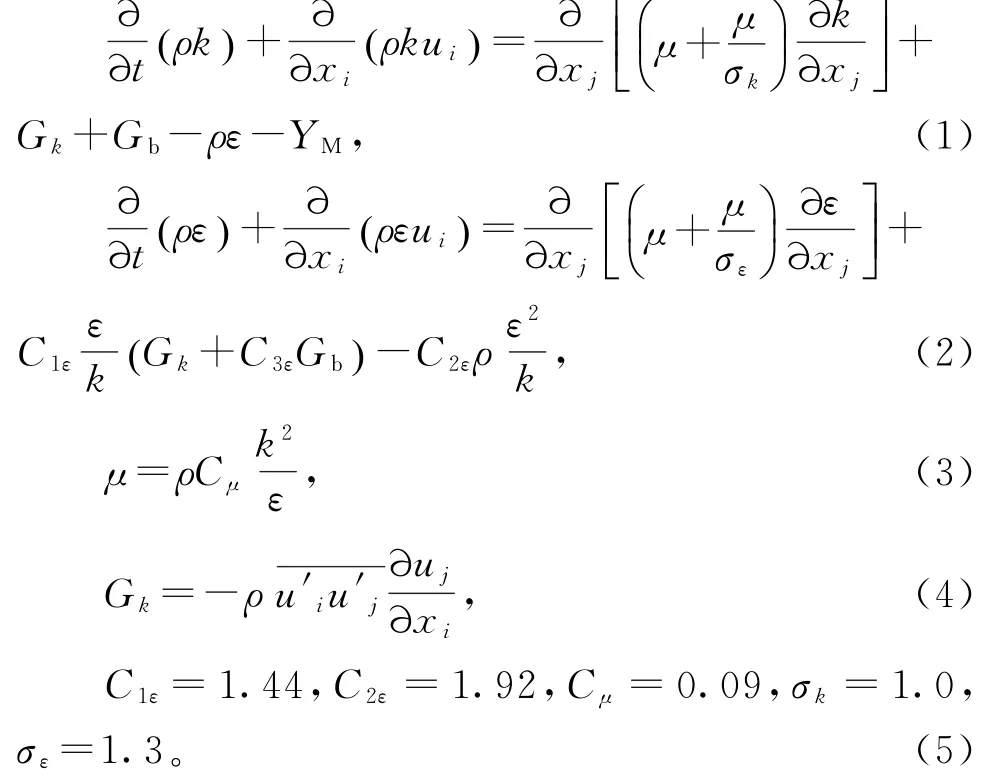
1.1.2 传热模型

能量方程由式(6)给出:

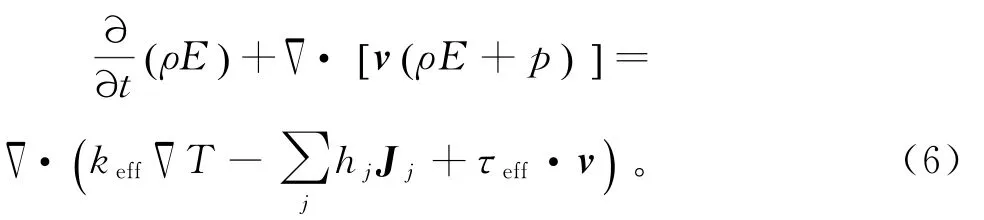
1.1.3 控制方程和求解方法

质量守恒方程,又称连续方程,如式(7)所示:

动量方程:

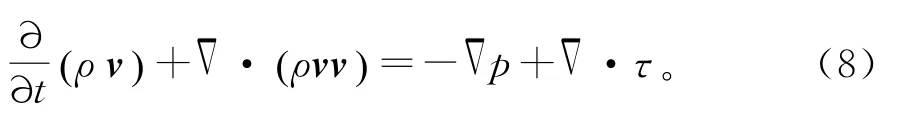
本研究使用基于压力的求解器,速度场的连续性约束是通过求解压力方程来实现的。压力-速度耦合算法使用SI MPLE,SI MPLE算法利用速度和压力修正之间的关系,来加强质量守恒并获得压力场。其中,压力插值格式使用PRESTO!。

1.2 物理模型

图1(a)是回转窑全尺寸结构图,图1(b)是图1(a)沿XY平面左右对称部分的右侧,结构尺寸如图1(b)所示,单位mm。其中,对称面由对称面1,对称面2和对称面3组成。

本研究的模型为图1(a)的对称面右侧部分,即图1(b)。热流进入的方向为负X方向,热流出口的方向为正Y方向,内筒轴线从右到左为正Z方向。其中,对称面2的中心位置为坐标原点O(0,0,0),如图1(b)所示。图1(c)是对回转窑进行网格划分图,首先对回转窑进行非结构性网格划分,但由于网格数过多,故对划分网格后的非结构性网格进行多面体转化。

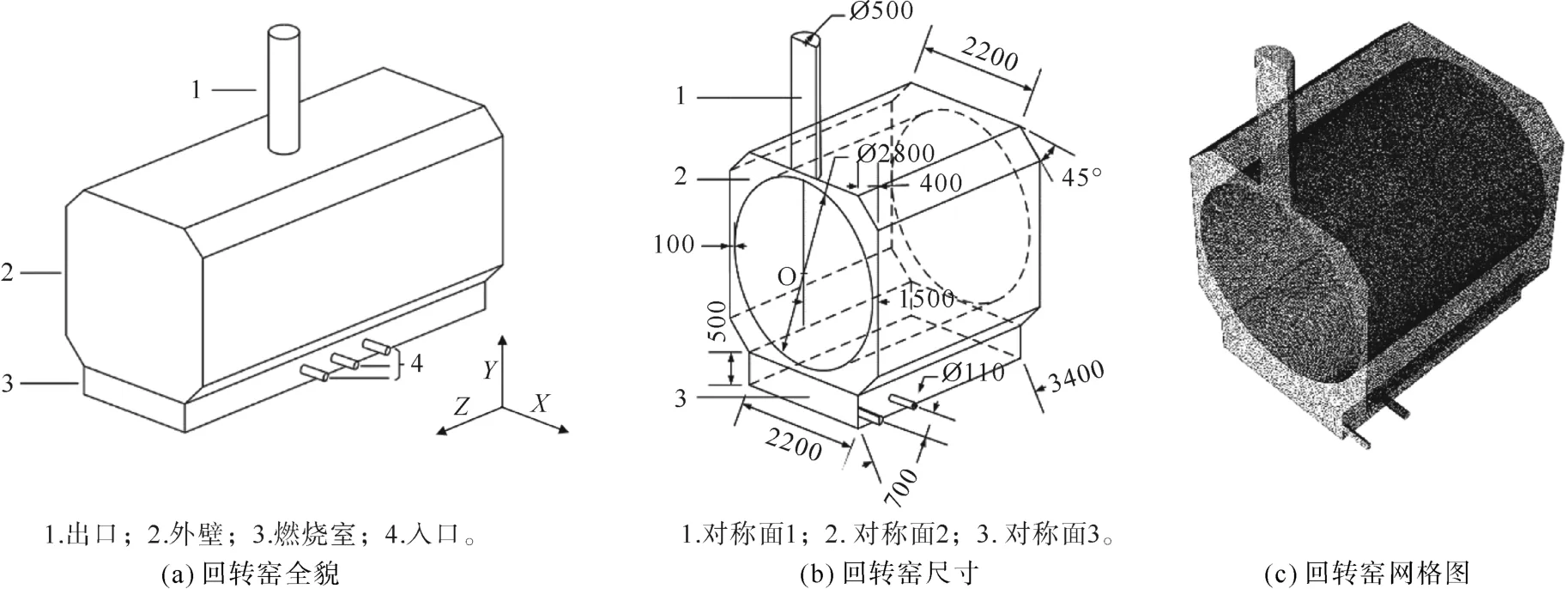
图1 回转窑结构和网格示意图Fig.1 Sche matic and grid diagra m of rotary kil n

2 模拟过程

2.1 边界条件

假设3个入口气体是已经燃烧后的高温混合理想气体,其组成为CO2,H2O,N2和O2,其中O2的摩尔分数占0.002,可以忽略不计。回转窑外壁边界光滑,无滑移,假设回转窑没有热损失,故热边界条件为绝热,即热通量为0。内筒壁边界为光滑,无滑移,热边界条件使用对流换热边界条件,表面传热系数(αin)为2 000 W·(m2·K)－1,内筒内侧冷流体温度(Tin)为673.15 K。回转窑内筒内侧冷流体温度是根据工业数据[21]确定的,而内筒壁表面传热系数是根据经验[22]确定的。具体数据如表1所示。

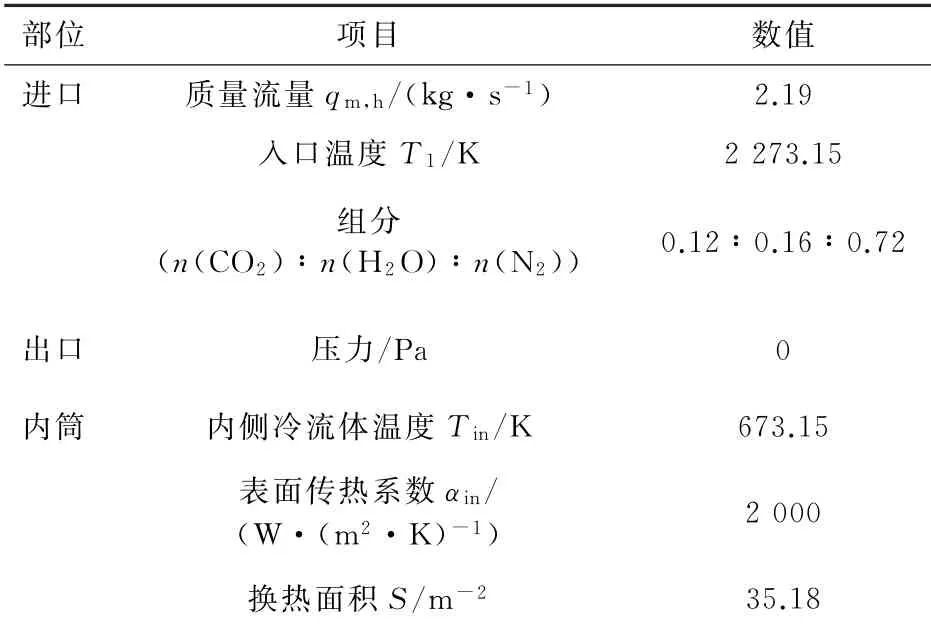
表1 边界条件Table 1 Boundary conditions

2.2 网格无关化验证

选取一条坐标为(－1 450,0,0)到(－1 450,0,－3 400)的直线,位置如图2所示,该直线位于内筒壁与回转窑外壁的中心,并且与Z坐标轴平行。在不同网格数目的情况下进行模拟,获得该直线上的速度的变化趋势,以进行网格无关化验证,见图3。从图3可以看出,当网格数低于432 433时,具有较大误差(大于2.5%),而网格数432 433与520 702的两条曲线比较接近,最大误差1.6%,可以认为满足模拟要求。因此,本研究选择432 433的网格数进行数值模拟。

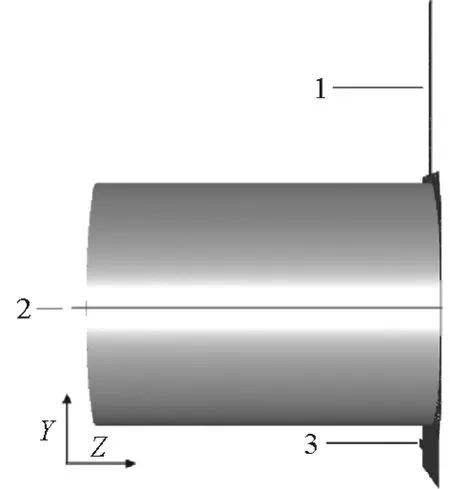
图2 直线的位置示意图Fig.2 Schematic diagra m of the position of the line

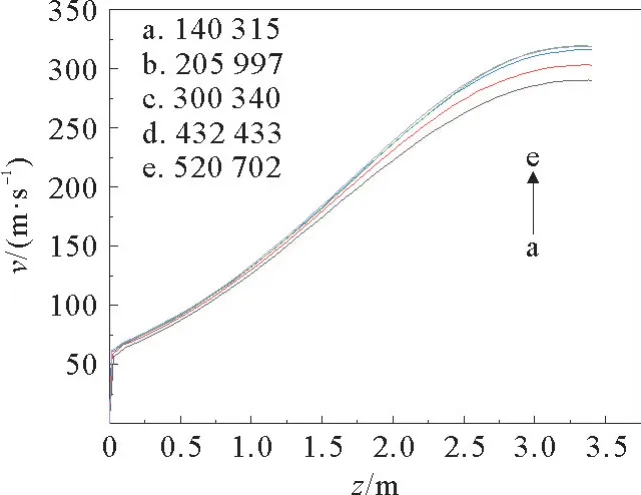
图3 直线上不同网格数的速度变化图Fig.3 Speed change graph of different grid nu mbers on a straight line

2.3 对流增强因子的确定

对流增强因子表示测量的努塞尔数与理想流量的努塞尔数之比。当模拟扰动流或扰动边界层的传热时,需要利用对流增强因子来增加扩散热通量的计算。工业上传统的回转窑出口温度T2为875.15 K,通过调节对流增强因子的数值模拟出口温度,与工业实际值进行比较。当对流增强因子等于38时,模拟的出口温度与实际数据相符合。

2.4 评价指标

本工作的研究对象是内筒外侧的传热情况,所以把外侧对流传热系数的大小作为回转窑传热性能的评价指标,以衡量添加折流板对传热的影响。假定内筒内侧冷流体的温度Tin和表面传热系数αin一定,并且忽略管壁导热热阻和污垢热阻影响,由式(9)可以计算总传热系数K,然后进一步由式(10)反推出内筒外侧的对流传热系数αo。式(9)中对数平均温差Δtm由公式(11)计算得出。

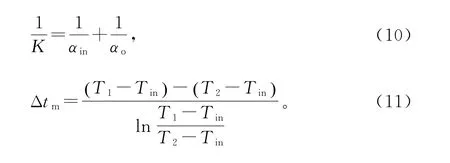
3 模拟结果与讨论

3.1 典型无折流板外热式回转窑流场分析

图4分别给出了不同视角下典型无折流板外热式回转窑内筒的温度分布云图。由图4看出,高温度区域集中位于对称面与内筒相交位置,如:图4(a)中1位置温度较高;而图4(b)中1位置较低。可见,典型无折流板外热式回转窑传热效率有很大的提升空间。为了探究其强化传热的提升空间并进行合理的优化,进一步对内筒的速度流场进行了分析。

图5为在图4相同视角下的典型无折流板外热式回转窑速度流线图。

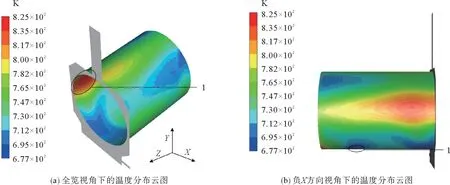
图4 无折流板外热式回转窑内筒温度分布云图Fig.4 Temperature contours of the inner cylinder of the unbaffled indirectly heated rotary kiln

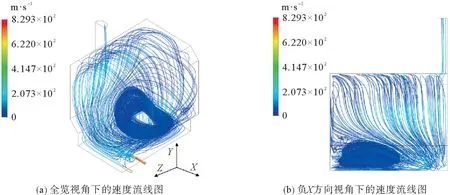
图5 无折流板外热式回转窑速度流线图Fig.5 Velocity streamline of unbaffled indirectly heated rotary kil n

结合图5(a)和(b)两张图可以看出,热流主体沿对称面绕内筒流过半圈后,直接从出口处流出,停留时间较短,并且内筒的左右两端附近区域流经的热流较少,在内筒负Y方向上存在很大的滞留区。对比图4、5发现,内筒壁温度高的区域,热流速度也快。因此,可以考虑通过添加折流板,在强化湍动的同时,改善热流体的停留时间,增加传热机会,避免短路和滞留区。

3.2 结构改进分析

综合以上对典型无折流板外热式回转窑温度云图和速度流线的分析,提出了通过添加折流板以强化传热的方案。折流板的位置及尺寸如图6所示。

本工作折流板的结构尺寸是根据经过前期理论分析和CFD初步模拟的结果最终确定的。折流板A部分(图6(a))是位于燃烧室顶面的正方形平面,厚度为0 mm,长3 300 mm,宽2 200 mm,方向为水平,高度为500 mm;折流板B部分(图6(b)、图6(c))是缠绕在内筒的螺旋形折流板,该折流板是由10个螺距300 mm、半径2 400 mm的螺旋形形成的,并且厚度为0,可以让内筒左右两底面的热流沿内筒绕流到对称面处汇集。这样可以增加热流与内筒的接触面积,消除热流滞留区,增加内筒面附近的湍动,提高对流传热系数,达到强化传热的目的。

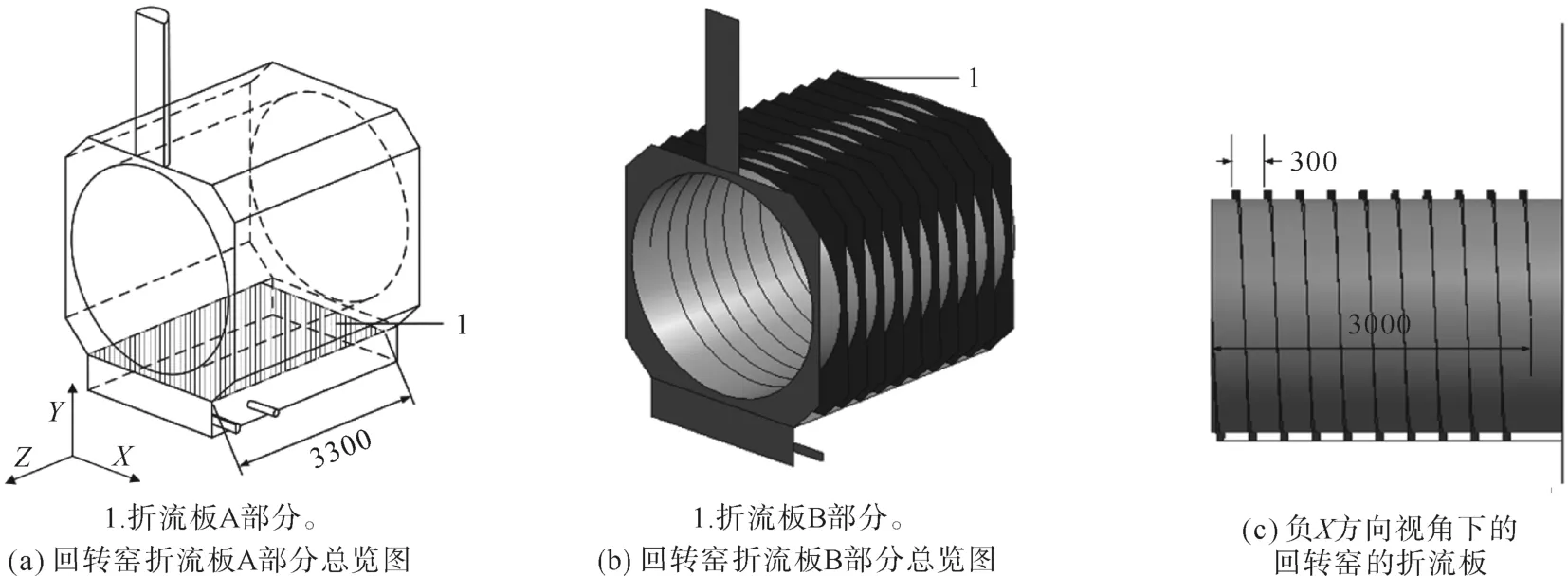
图6 有折流板外热式回转窑示意图Fig.6 Sche matic diagra m of indirectly heated r otar y kiln with baffles

3.3 有折流板外热式回转窑流场分析

图7分别给出了不同视角下有折流板外热式回转窑内筒的温度分布云图,图中用不同数字表征了温度变化的特征位置标记。由图7可以看出,图7(b)中1位置温度较高;而图7(a)中1位置较低。从图7中可以看出,折流板的加入使内筒的侧面温度由底面向对称面逐渐降低。

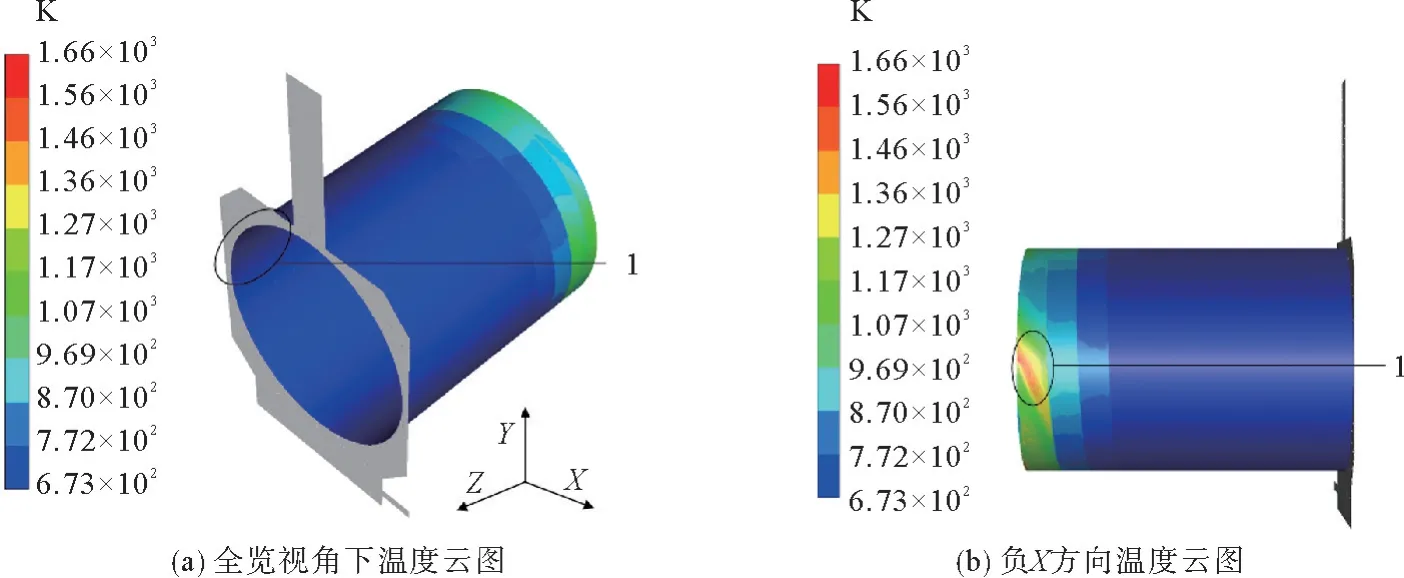
图7 有折流板外热式回转窑内筒温度云图Fig.7 Temperat ure contours of inner cylinder of indirectly heated rotar y kiln with baffles

图8分别给出了不同视角下有折流板外热式回转窑的速度流线图,图中不同数字表征了温度变化的特征位置标记。与图7温度分布对比可知,热流速度越快,内筒壁温度越高,即图7(b)和图8(b)中1位置所示。由于折流板B部分的螺旋折流板的螺旋几何形状的影响,Z轴方向上的流体流动增强并变成平推流。折流板B部分的螺旋折流板的挡板间距为300 mm,对应的平均环空流体路径长度为8 801.4 mm。这表明使用螺旋折流板的回转窑更紧凑,而不显著增加其尺寸和质量。与图5相比,折流板的添加,使得内筒上的热流速度分布更加均匀,减小了流动滞留区。同时折流板的添加,增加了热流在回转窑间隙的停留时间,增加了扰动,增加了换热面积,利于强化传热。

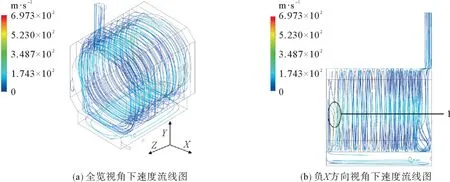
图8 有折流板外热式回转窑速度流线图Fig.8 Velocity strea mline of baffle rotary kil n

3.4 增加折流板后的效果比较

为了更明确地显示增加折流板的效果,分别计算了有、无折流板情况下内筒外侧的对流传热系数,如表2所示。具体计算方法:首先,式(11)计算出对数平均温差(Δtm);然后由式(9)求出总传热系数(K),即K＝QT/(S·Δtm);最后由式(10)计算出内筒外侧的对流传热系数(αo),即αo＝K·αin/(αin－K)。

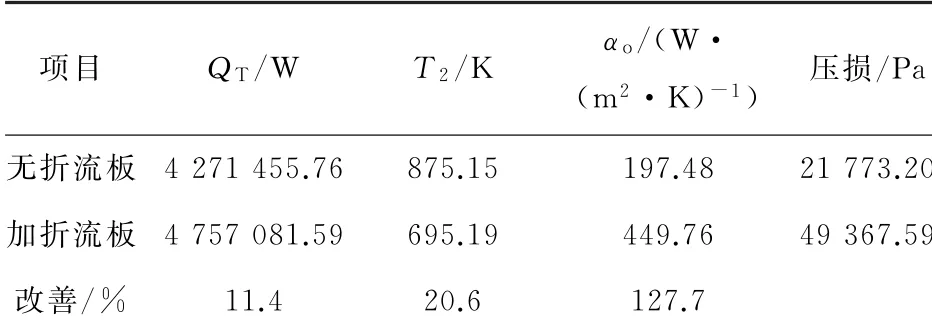
表2 内筒外侧对流传热系数Table 2 Convection heat transfer coefficient of the inner cylinder

从表2中可以看出,与无折流板相比,添加折流板后,内筒外侧的传热系数提升了127.7%,出口温度降低了20.6%,传热热流量提升了11.4%。因此,折流板的添加显著增强了传热效果。另外,加挡板的压损是无挡板的2.27倍。故增加的压损与增加的传热流量相比,可以接受。

4 结 论

1)在外热式回转窑物理模型的基础上,基于工业数据,建立了回转窑加热过程的计算流体力学(CFD)模型,结合温度云图和速度流线图发现:内筒左右两端附近区域是传热瓶颈。

2)通过增加折流板结构优化外热式回转窑传热,模拟结果表明:在压损不大的情况下,内筒外侧表面对流传热系数提升了127.7%,传热热流量提升了11.4%。

符 号 说 明

C1ε,C2ε,C3ε,Cμ——常量

E——总能量,J

Gb——浮力产生的湍流动能项,kg·(m·s3)－1

Gk——平均速度梯度产生的湍流动能项,kg·(m·s3)－1

h j——组分j的显焓,J·kg－1

J j——组分j的扩散通量,kg·(m2·s)－1

K——总传热系数,W·(m2·K)－1

k——湍流动能,m2·s－2

keff——有效导热系数,W·(m·K)－1

p——压力,Pa

QT——内筒的传热热流量,W

qm,h——质量流量,kg·s－1

S——换热面积,m2

T——温度,K

t——时间,s

Δtm——对数平均温差,K

u i,u j——速度分量,m·s－1

v——总速度矢量,m·s－1

YM——可压缩湍流中脉动膨胀对总耗散率的贡献,kg·(m·s3)－1

α——传热系数,W·(m2·K)－1

μ——湍流黏度,Pa·s

ρ——密度,kg·m－3

σk,σε——k,ε的湍流Prandtl数

ε——湍动能耗散率,m2·s－3

τ——应力张量,Pa

下标

in——内筒内侧

o——内筒外侧

1——入口

2——出口