变流速条件下非达西裂隙流溶质运移特征研究
2021-06-09苏世林许光泉
李 旭,苏世林,文 章,许光泉
(1.安徽理工大学地球与环境学院,安徽 淮南 232001;2.中国地质大学(武汉)环境学院,湖北 武汉 430078)
裂隙介质广泛存在于自然界中,与人类的生产生活活动密切相关。裂隙介质中地下水渗流和溶质运移规律的研究一直是国内外学者重点关注的问题之一,但是由于裂隙介质具有强烈的空间变异性,使得溶质运移特性研究变得十分复杂[1-4]。近几十年来,国内外学者对此开展了大量的研究,并取得了一定的研究进展,其主要研究成果可分为两大类:第一类为裂隙网格中水流和溶质运移理论研究[5-6];第二类为单裂隙介质中水流和溶质运移理论研究[7-10]。单裂隙作为裂隙介质水流和溶质运移研究的基础单元,多数研究通常是从单裂隙开始的。如郑志成等[8]利用平行大理石板开展了单个裂隙溶质运移实验研究,结果表明溶质的穿透曲线表现出拖尾的现象。因此,开展单裂隙溶质运移理论研究对于探索裂隙介质中溶质运移规律具有重要的理论意义。
通常情况下,单裂隙溶质运移理论研究主要是在达西流的基础上进行的[11-12],然而越来越多的研究表明达西定律只在一定的水力梯度范围内成立,裂隙介质中地下水流速过快往往会导致地下水渗流速度与水力梯度呈非线性关系,即所谓的非达西流[13-16]。Qian等[17]通过单裂隙室内实验研究发现,单裂隙介质中地下水平均流速和水力梯度的关系能很好地与Izbash方程吻合,且水流速度与水力梯度的1/2次方成正比;李一鸣等[18]利用Izbash方程刻画了单裂隙介质中的非达西流,研究当单裂隙的轴向与基岩水流方向斜交过程中,裂隙流的非达西程度对溶质羽分布的影响。上述研究表明,Izbash方程能够很好地描述单裂隙介质中的非达西流,可以应用于单裂隙介质中溶质运移机理的研究。
目前国内外学者对单裂隙的非达西渗流和溶质运移开展了大量的理论研究,其研究通常假定地下水流是稳定的[19-21]。然而,实际裂隙含水层由于受到补给/排泄模式、地表水体水位以及区域地下水抽采率的变化等因素的影响,导致裂隙介质中地下水流速是随时间发生变化的[22]。目前许多学者也开展了变流速条件下的溶质运移理论研究[22-24]。如Singh等[24]利用拉普拉斯变换得到了地下水流速为正弦变化的二维溶质运移的解析解;Li等[22]以松散含水层为研究对象,提出了指数变化的地下水流速方程,并利用积分变换获得变流速淋滤作用下的一维溶质运移的解析解。目前关于变流速条件下的溶质运移理论研究对象主要为松散含水层,而裂隙含水层中的变流速溶质运移研究几乎还是空白。此外,裂隙介质溶质运移过程中的地下水流时常不符合达西定律。因此,有必要开展变流速条件下非达西裂隙流溶质运移规律的研究。
为此,本文将建立变流速条件下考虑非达西流的单裂隙一维溶质运移模型。利用指数变化的地下水流速方程来刻画单裂隙介质中地下水流速的变化规律,并耦合Izbash方程,利用积分变换的方法获得变流速条件下单裂隙非达西流溶质运移的解析解,以此来探究非达西流和指数变化的地下水流速对裂隙介质中溶质运移的影响机理,以为裂隙地下水污染研究提供理论依据。
1 非达西渗流与变流速水流
1.1 裂隙达西流与非达西流
在裂隙介质中,当地下水流速较小时,黏滞力占主导地位,惯性力的影响可以忽略,通常用线性的达西定律来表示,即:
vd=-KJ
(1)
式中:vd为达西渗流速度[L/T];J为水力梯度[无量纲];K为裂隙介质的渗透系数[L/T]。
但当地下水流速较大、惯性力占主导地位时,地下水流速与水力梯度之间不再呈现线性的关系,发生非达西渗流。为此,国内外学者提出了不同类型的非线性流方程,在方程中因参数太多,限制了其应用[13]。本文采用Izbash方程来描述裂隙介质中的非达西渗流[18],其数学表达式为
vn=-kJ
(2)
式中:n为经验系数,n值反映了裂隙水流流态的变化,即从达西流(n=1)到非达西流(1 裂隙水流动状态依据雷诺数(Re)判定,其判定方程为 (3) 式中:2b为裂隙的平均开度[L];q为裂隙介质中地下水平均流速[L/T];μ为地下水动力黏度[L2/T]。 通常情况下,裂隙中水流的Re大于1~10之间的某个值时,地下水渗流速度与水力梯度之间不再呈现线性的关系,而表现出非达西渗流的现象。 目前关于裂隙介质溶质运移模型中地下水流速通常设定为常数,但实际过程中地下水流速是随着时间的变化而发生变化的(见图1),针对这一问题,提出了采用线性方程和指数变化的方程来刻画地下水流速的变化规律。实际上裂隙介质中地下水流速的变化应趋于某一确定的值,表现出指数增加或指数衰减的趋势[22]。例如,当含水层受到生物、化学及物理的堵塞会导致其渗透性减小,使得含水层中地下水流速表现出指数衰减[25-26]。再如,河岸带及海岸带的裂隙含水层由于地表水位的波动(如洪水、潮汐等作用)也会引起含水层中地下水流速呈现出指数增加或指数衰减的趋势[23]。因此,在达西流条件下的裂隙含水层中地下水流速可以表示为指数增加或指数衰减的形式[22]: 图1 变流速条件下非达西裂隙流溶质运移示意图Fig.1 Schematic diagram of solute transport under Non-Darcian flow and variable flow velocity in the fracture vd(t)=vd0φ(t)=vd1+(vd0-vd1)(e-λt) (4) 式中:vd0为单裂隙介质中初始的地下水流速[L/T];vd1为单裂隙介质中最终稳定的地下水流速[L/T];λ为地下水流速变化指数[1/T]。 当vd0>vd1时,公式(4)表示地下水流速为指数衰减的情况;当vd0 [v(t)]n=[v0τ(t)]n=(v1)n+[(v0)n-(v1)n](e-λt) (5) 式中:v0为非达西流条件下单裂隙介质中初始的地下水流速[L/T];v1为非达西流条件下最终稳定的地下水流速[L/T]。 若n=1时,公式(5)与公式(4)相同,则τ(t)可表示为 (6) 在建立变流速条件下非达西裂隙流一维溶质运移模型之前,为了简化数学模型,假设条件为:①裂隙为单裂隙,其水流为非达西一维流动;②裂隙的开度不随距离变化而变化,不考虑裂隙的粗糙度及充填物等因素的影响;③地下水流为非稳定流,其流速随时间呈指数变化;④溶质为惰性溶质。则单裂隙介质中对流-弥散方程(ADE)可以表示为 (7) 式中:C为单裂隙介质中溶质的浓度[M/L3];x为距离[L];t为时间[T];D(t)为随时间变化的弥散系数[L2/T],v(t)为随时间变化的地下水流速[L/T],两者分别表示如下: v(t)=v0τ(t) D(t)=αv(t)=αv0τ(t)=D0τ(t) (8) 式中:α为弥散度[L]。 将公式(8)代入到公式(7)中,可得: (9) 初始条件和边界条件可表示如下: C(r,0)=0,x<0 (10) C(0,t)=C0,t>0 (11) C(∞,t)=0,t>0 (12) 式中:C0为x=0处给定的溶质浓度[M/L3]。 为了获取模型的解,这里引入一个新的积分变换: (13) 则公式(9)可以表示为 (14) 边界条件和初始条件在相同的积分变化下可以表示如下: C(x,0)=0,x<0 (15) C(0,T)=C0,T>0 (16) C(∞,T)=0,T>0 (17) 通过积分变换,公式(13)~(16)为经典的ADE模型。因此,一维半无限长单裂隙介质在x-T域中定浓度边界条件下ADE模型的解为 (18) 式中:erfc(·)为余误差函数。 将公式(13)代入到公式(17)中,可获得一维半无限长单裂隙介质在x-t域中定浓度边界条件下ADE模型的解为 (19) 上述推导的公式(19)为变流速条件下非达西裂隙流溶质运移模型的解析解。为了进一步验证该模型的准确性,将不考虑非达西流的溶质运移结果,将本文模型解析解与Li等[22]的模型解析解进行了对比。Li等[22]提出了指数变化的地下水流速方程,并获得了变流速条件下一维溶质运移模型的解析解,但是该模型没有考虑非达西流的影响。当非达西参数n=1时,本文模型解析解结果应该与Li等[22]模型解析解结果一致。图2为本文与Li等[22]模型解析解在x=20 m处的溶质穿透曲线(BTC)对比结果。模型主要参数设置如下:n=1,v0=1×10-3m/s,v1=6×10-3m/s,λ=0.000 01 1/s,α=0.1 m、0.5 m和2 m。 图2 本文与Li等[22]模型解析解在x=20 m处的溶质 穿透曲线对比Fig.2 Comparison of the breakthrough curves at x=20 m computed by analytical solution of this study and Li et al.[22] 由图2可见,本文模型解析解结果与Li等[22]模型解析解结果完全吻合,进一步说明本文的解析模型是准确的。 为了研究非达西流对单裂隙介质中溶质运移的影响,首先应确定非达西裂隙流地下水流速的范围。本文将发生非达西流与达西流流态转变的临界雷诺数设定为10,由公式(3)可得到单裂隙介质中临界地下水流速的计算公式为 (20) 将参数设置为:2b=0.02 m,μ=1.0×10-6m2/s[18],根据公式(20),可计算得到单裂隙介质中临界地下水流速为0.000 5 m/s。 当裂隙介质中地下水流速为指数衰减条件下,在距离原始溶质注入点x=40 m处,当非达西参数n取不同值时的溶质穿透曲线,见图3。模型主要参数设置如下:v0=0.001 5 m/s,v1=0.000 5 m/s,λ=0.000 05 1/s,α=0.1 m,n=1、1.2、1.5和2.0。 图3 变流速条件下不同非达西参数n在x=40 m处 所对应的溶质穿透曲线Fig.3 Breakthrough curves for different Non-Darcian parameters (n) at x=40 m under variable flow velocity 由图3可见,溶质穿透曲线的溶质浓度随着非达西参数n的增大而不断增大,表明非达西参数n越大,地下水紊流程度越高,溶质运移速度越快。 为了进一步分析导致溶质运移速度变快的原因,本文研究了不同非达西参数n时单裂隙介质中地下水流速v的变化,其变化曲线见图4。 图4 不同非达西参数n下单裂隙介质中地下水流 速的变化曲线Fig.4 Velocity curves of the groundwater flow in a single fracture for different Non-Darcian parameters (n) 由图4可见,当裂隙介质中地下水流速由0.001 5 m/s减小到0.000 5 m/s时,非达西参数n越大,地下水流速衰减得越慢,地下水流速越快。总之,在变流速条件下裂隙介质中的溶质运移受到非达西流的影响明显,非达西流的存在改变了裂隙介质中地下水流速的变化规律。因此,在裂隙介质中刻画变流速溶质运移过程不能忽视非达西流因素的影响。 非达西流条件下地下水流速衰减指数λ取不同值时在x=40 m处所对应的溶质穿透曲线,见图5。模型主要参数设置如下:v0=0.001 5 m/s,v1= 0.000 5 m/s,α=0.2 m,n=1.5,λ=0.000 025 1/s、0.000 050 1/s和0.000 075 1/s。对于指数衰减的地下水流速,λ值的大小反映了地下水流速衰减得快慢,主要是由地下水水位变化速率或者渗透性衰减得快慢所决定的。 图5 非达西流条件下不同取值的地下水流速衰减指数 λ在x=40 m处所对应的溶质穿透曲线Fig.5 Breakthrough curves for different attenuation indexes λ of the exponentially decreasing groundwater velocity at x=40 m under Non-Darcian flow 由图5可见,地下水流速衰减指数λ越大,溶质穿透曲线的溶质浓度越小,说明地下水流速衰减指数λ越大,溶质运移速度越慢。这主要是由于地下水流速衰减指数λ越大,地下水流速衰减得越快,导致溶质运移速度越慢。当v1=0.001 5 m/s时,地下水为稳定流,本文通过对比变流速条件下的溶质穿透曲线与稳定流的溶质穿透曲线可以发现,变流速条件下溶质穿透曲线的溶质浓度值均小于地下水稳定流的情况,说明地下水流速的变化对裂隙介质中溶质运移有较大的影响。 非达西流条件下地下水流速v1取不同值时在x=40 m处所对应的溶质穿透曲线,见图6。模型主要参数设置如下:v0=0.001 5 m/s,λ=0.000 050 1/s,α=0.2 m,n=1.5,v1=0.000 7 m/s、0.001 1 m/s、0.001 5 m/s、0.001 9 m/s和0.002 3 m/s。当地下水流速v1取不同值时,公式(2)可以表示为地下水流速指数增加或指数衰减的函数形式。因此,当v1>0.001 5 m/s 时,地下水流速为指数增加的函数形式;当v1<0.001 5 m/s 时,地下水流速为指数衰减的形式;当v1=0.001 5 m/s 时,地下水为稳定流。 图6 非达西流条件下不同v1取值在x=40 m处所 对应的溶质穿透曲线Fig.6 Breakthrough curves for different final steady velocities (v1) at x=40 m under Non-Darcian flow 由图6可见,地下水流速v1越小,地下水流速衰减的幅度越大,溶质穿透曲线的溶质浓度越小,溶质运移速度越慢。例如,当v1=0.000 7 m/s时,溶质运移速度最慢,其溶质穿透曲线位于最右端(见图6)。另外,地下水流速v1越大,地下水流速增加的幅度越大,溶质穿透曲线的溶质浓度越大,溶质运移速度越快。因此,利用公式(2)可以刻画裂隙介质中地下水流速的指数增加或指数衰减的情况,为研究地下水流速变化对溶质运移的影响提供了有效途径。 本文依据Izbash和指数变化的地下水流速方程建立了单裂隙介质非达西流溶质运移新模型,通过积分变换的方法得到了模型的解析解,并模拟分析了非达西流和指数变化的地下水流速对裂隙介质中溶质运移的影响,得到如下结论: (1) 变流速条件下,单裂隙介质中非达西参数n越大,地下水紊流越强,地下水流速越大,导致溶质运移速度越快,溶质穿透曲线的溶质浓度越高。因此,单裂隙介质中刻画变流速溶质运移过程不能忽视非达西流因素的影响。 (2) 单裂隙介质中指数变化的地下水流速对溶质运移有较大的影响,地下水流速的衰减指数λ越大,地下水流速衰减得越快,溶质穿透曲线的溶质浓度越低,溶质运移速度越慢。 (3) 地下水流速(或渐进地下水流速)在单裂隙介质溶质运移过程中起到了关键的作用,其大小反映了地下水流速增加或减小的幅度,其变化的幅度越大,溶质运移速度快慢表现得越明显。1.2 变流速水流

2 数学模型及求解

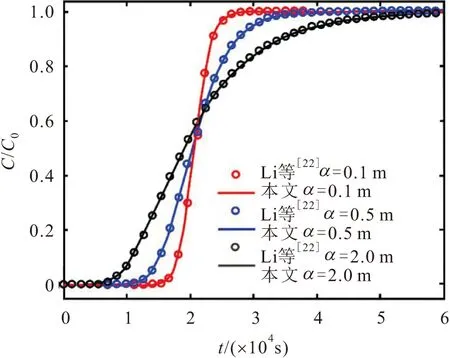
3 结果分析与讨论
3.1 非达西裂隙流的溶质运移特征
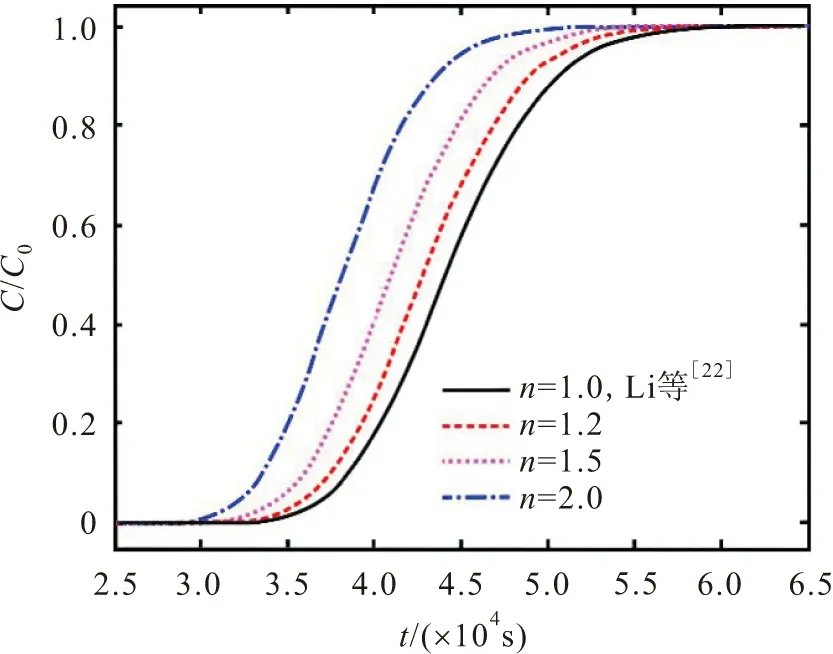
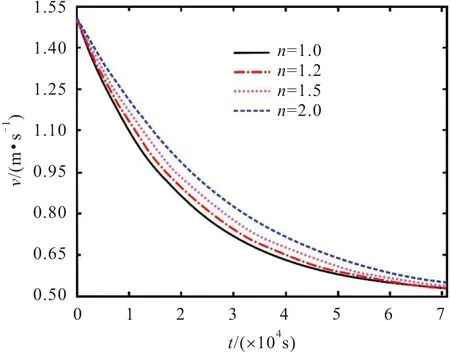
3.2 变流速条件下非达西流裂隙流的溶质运移特征

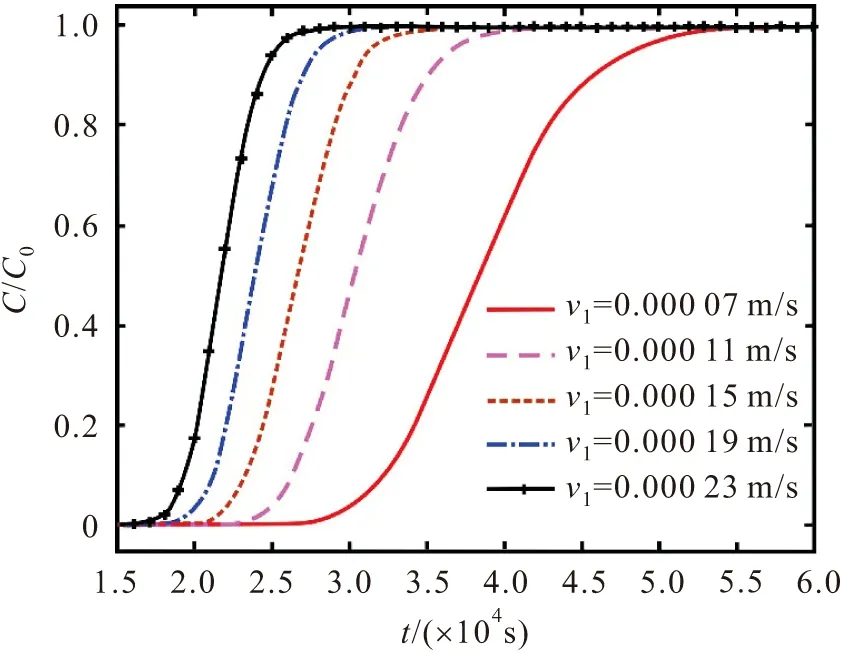
4 结 论
