基于CFD的涡轮式搅拌器内流场数值模拟

杨文哲 苏晓磊 刘毅 冯亚斌

摘   要： 搅拌器内流场的计算流体力学（CFD）数值模拟中，网格离散质量对流场仿真结果的可靠性具有重大影响。基于ANSYS ICEM CFD仿真环境，以六直叶开启涡轮式搅拌器为研究对象，提出一种六面体网格离散方法，并采用标准k-ε湍流模型和滑移网格模型（SM）对流场进行数值模拟。研究发现：1）在六面体网格离散下，搅拌器内流场网格质量较好，平均网格质量约为0.96，能够很好地刻画径向流的典型特征并较为准确地模拟搅拌器内流场问题;2）所模拟的六直叶开启涡轮式搅拌器混合效果较差，在靠近釜顶、搅拌轴区域与釜底的“锥形区域”内易形成回流死区，造成物料堆积，应通过安装诱导锥、适当降低搅拌器的安装位置等方式减小回流死区，以提高搅拌器的混合效果。

关键词： 六直叶开启涡轮式搅拌器;ANSYS ICEM CFD;网格离散;数值模拟

引言

当今，CFD（计算流体力学）理论和软件迅速發展，已成为一种先进且高效的研究工具，在航空航天、土木工程和化学工业等领域应用广泛[1-3]。

在化工生产过程中，搅拌器对流体的混合、物料的分散等都有着重要作用。近些年来，越来越多的学者已开始利用CFD与PIV（粒子图像测速）技术获取搅拌器内流场的重要信息，从而实现搅拌器的优化设计[4-6]。例如，Luan等[7]利用CFD技术研究了6-PBT搅拌器的偏心距和底部间隙对搅拌釜中假塑性流体混合特性的影响，结果表明流场的微观结构对示踪剂的混合过程具有重要影响。Zhang等[8]采用Fluent软件的滑移网格模型（SM）对所设计的新型圆筒搅拌器进行了数值模拟，评估了其混合特性，结果表明圆筒搅拌器相比Rushton涡轮与螺旋桨涡轮具有更好的节能效果。Jiang等[9]采用4种不同的搅拌器合成了Y2O3粉体，并研究了共沉淀反应过程的均匀性对Y2O3粉体、前驱体相组成和形貌的影响，结果表明采用四斜叶涡轮可以获得更均匀混合物，所制备的Y2O3粉体更分散。Li等[10]利用混合网格对搅拌釜内流场进行了离散，研究了搅拌釜敞口无挡板且釜内具有自由表面涡流时的流场分布，并通过预测数据与实验数据的对比，验证了仿真的可靠性与准确性。莫惠珺等[11]对4种不同型式结构的双曲面搅拌器内流场进行了数值模拟研究，结果表明高叶片结构的双曲面搅拌器更有利于形成对称均匀的流场，搅拌混合效果更佳。胡志梁等[12]采用层流模型与大涡模拟方法对六直叶搅拌器中低雷诺数下的拟塑性流体流动特性进行了研究，为搅拌器的设计及实际搅拌的操作提供了参考。张慧敏等[13]模拟研究了开启涡轮式搅拌器内流场，并与PIV实验进行了验证，结果表明模拟计算结果与实验结果基本一致，优化叶轮设计参数后的搅拌器内流场中的搅拌死区最少，搅拌效果最佳。

可以看出，搅拌器内流场的研究工作已越来越依赖于CFD仿真，而仿真的前提是网格离散，网格离散质量会对流场仿真结果的可靠性产生重大影响[14-16]。为此，本文以六直叶开启涡轮式搅拌器为研究对象，采用ANSYS ICEM CFD软件探索适合于该搅拌器内流场的网格剖分方法，并对搅拌器内的流动特性进行探讨，最大程度减小回流死区。

1  物理模型及网格划分

1.1  物理模型与计算域

采用SolidWorks 2018软件建立搅拌器的几何模型[17]，如图1所示。模型主要由釜体、碟形釜底、挡板、搅拌器和搅拌轴五部分组成，搅拌器采用垂直定位，旋转方向为顺时针。搅拌釜和叶轮的主要参数如表1所示。简化后的计算域与边界条件如图2所示，整个计算域被分为动、静两个区域。动区域与静区域分别采用旋转坐标系和静止坐标系，其交界面的信息以插值形式进行数据传递。若要捕捉搅拌器和挡板附近的流动细节，可进行局部网格加密处理[18]，并注意第一层网格节点高度y的设置。

1.2  网格划分

1.2.1  动区域网格划分

将动区域分割为6个单叶片区域，对其中之一进行网格划分。在完成关联几何体和块、设置网格尺寸与周期性节点、更新预览网格、检查网格质量、调节优化网格等相关操作后，所生成的单叶片区域块与网格如图3所示。

动区域的块与网格可通过旋转复制单叶片区域块的方式来生成;若发生错误，一定要检查周期性面与边的关联情况。所生成的动区域块与网格如图4所示，其六面体网格总数为93 712。

1.2.2  静区域网格划分

静区域网格的划分方式可采用类似于动区域网格的划分方式。将挡板类比于叶片，再通过旋转复制单个挡板区域块的方式来生成釜体静区域的块与网格。值得注意的是，在旋转复制块以前，必须删除动区域单叶片的块，并创建好周期性节点，完成周期性面与边的关联，以避免映射错误的发生。但由于碟形釜底静区域的网格不易划分，故可采用首先单独对其划分，再与釜体静区域其他网格进行合并的方法来完成。其交界面的信息也以插值形式进行数据传递。现说明釜底静区域的网格划分方式。首先将釜底区域块划分为16个子块，再对其进行“O”型剖分，使釜底的块能够更好地贴近釜底面，以提高釜底面附近聚集的网格节点效率[19]，从而提高网格质量。所生成的釜底区域块与网格如图5所示，釜底区域的六面体网格总数为189 310。

1.2.3  合并动、静区域网格及检查

对所划分的动、静区域网格进行合并后，一定要利用Check Mesh选项卡来检查可能出现的网格错误，比如重复的网格元素、丢失的面网格等。若发现错误，可采用Mesh Repair Tools功能进行修复。经检查无误后，所得到搅拌釜内流场网格如图6所示。图6b中的深色外围区域与中间区域分别为挡板和搅拌器。搅拌釜内流场整体区域的六面体网格总数为486 398。

1.3  网格质量检查

采用Edit Mesh命令中的Display Mesh Quality功能进行网格质量检查。网格度量参数如表2所示，除最小角度指标外，各参数的值越接近1，表示所生成的网格质量越好，而最小角度的指标值越接近90°越好[16，17，19，20]。釜底面的曲率半径较大，与水平面的夹角较小，是造成整体网格长宽比指标值较低（未能达到0.3以上）的主要原因，但其余各指标值均在0.3以上。如果所检测的各评价指标值较低，则网格质量较差，可通过调节节点函数与移动节点的方式来提高网格质量，而网格的大小则可通过调节比例缩放因子的方法来调整，以便对其进行网格无关性验证。总的来说，由六面体网格所划分的搅拌器内流场网格质量较好（平均网格质量为0.96，接近1），但还应结合实际的流场计算结果进行对比分析。

2  数学模型及计算方法

由于本文所选案例的雷诺数在4 000以上，流态为完全湍流[12]，故选择适用于高雷诺数的湍流模型——标准湍流模型。描述水流的质量守恒方程、动量守恒方程和标准湍流模型方程如下[21-23]。

采用标准湍流模型与多参考模型（MRF）进行单相流数值模拟，流动介质为水，设置为不可压缩流动。压力与速度耦合求解选用SIMPLE算法，对流扩散项采用二阶迎风格式。计算域与边界条件可参考图2，搅拌器的转速设置为100 r/min。壁面边界采用无滑移边界条件，近壁处理为标准壁面函数。迭代步数为2 000步，残差收敛精度为10-4。在稳态的残差曲线收敛后，转为瞬态，并采用滑移网格模型继续进行求解计算，直至收敛。时间步长取为0.001，计算周期为6T（一般可选取3～6个周期）。

3  数值模拟结果与分析

3.1  流场分布

分别记轴向截面Y=0和径向截面Z=0为Y0和Z0。图7为Y0的速度矢量与流线图，其长度矢量与速度的范数成正比[24]。可以看出，液体在釜内轴向形成了“双循环”流型[18，24，25]，轴向“下循环”的搅拌效果要优于轴向“上循环”，越靠近釜顶和搅拌轴，搅拌效果越差，越易形成死区[4，26]。同时还可以看出，搅拌器所形成的涡旋较为发散，涡心位置较靠近挡板，不利于物料的混合。对此，可采用双层涡轮式搅拌器来代替单层涡轮式搅拌器，以提高搅拌效果[5]。此外，在搅拌器下方连接釜底的“锥形区域”内，形成了沿轴向呈对称分布的双环形小涡（回流死区），其混合效果较差，易造成物料堆积，可通过安装诱导锥的方式来减小回流区，并增大湍流强度[27];同时，该釜底回流死区的范围与离底高度成正比，可适当降低搅拌器的安装位置来减小釜底回流死区[5]。

3.2  湍动能与湍流耗散率分布

图8a为Z0的湍动能云图，现将其划分为三个区域，即挡板区域、叶轮区域和叶轮与挡板间的环流区域[24]。由于叶轮区域的湍动能大于环流区域与挡板区域，因此叶轮区域高度湍动，搅拌效果最好，其次为环流区域，而挡板区域搅拌效果最差，易形成死角。图8b为Z0的湍流耗散率云图，叶轮后方的尾涡区域湍流耗散率相比其他区域较高，且沿搅拌器中心呈周向分布，表明该区域的能耗较高，應适当减小，以降低搅拌器的功率消耗。

3.3  速度分布

图9a为Z0的速度云图与矢量图。可以看出，叶轮区域的流体速度相比环流区域较大，尤其在叶轮外缘切向速度最大，其有利于叶轮搅拌区的分散与混合作用[28]。环流区域的稳定性较好，但相比叶轮区域湍动性较差，叶轮后方的尾涡会使功耗增大，应尽量避免。同时从图9b中发现，叶轮外缘区域的液体旋向与环流区相反，这可能是因为速度延迟效应存在于叶轮外缘区域。

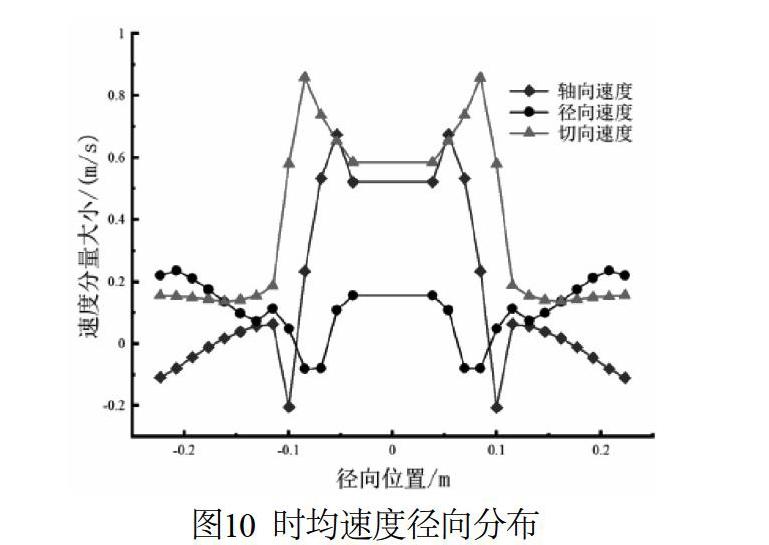
图10为横截面上（Z=0）的时均速度径向分布，取左侧区间（X=[-0.3， 0]）进行分析，可以看出各速度分量沿轴向呈对称分布且不失一般性。叶轮区域以切向流为主、轴向流为辅，径向速度小于切向速度，且峰值约为切速度峰值的0.25倍。速度的负号反映了回流区的存在[26]，轴向速度从几何中心向壁面呈先增后减再增再减的趋势，速度符号变化了两次，这说明液体参与了轴向的“双循环”流型，其峰值处可认为是叶轮的射流区[25]。从径向速度分布可以发现，叶轮区域与环流区的液体旋向相反且在叶轮后方存在尾涡，与图9b的Z0速度矢量分布一致。

图11为釜底横截面上（Z=0.18）的轴向速度径向分布，取左侧区间（X=[-0.216， 0]）进行分析可以看出，轴向速度呈对称分布，且其正负号变化了两次并有第三次变化的趋势，这说明釜底的“锥形区域”内存在两个环形小涡，与图7b所示的釜底流线分布一致，应尽量避免。

4  结束语

为研究六直叶开启涡轮式搅拌器内流场的网格划分方法与其流动特性，采用ANSYS ICEM CFD软件，对搅拌器进行了建模与数值模拟分析，得到以下结论：

（1）由六面体网格所离散的搅拌器内流场网格质量较好，平均网格质量可达到0.96，能够很好地刻画径向流的典型特征，并较准确地模拟搅拌器内流场问题。

（2）所模拟的六直叶开启涡轮式搅拌器混合效果较差，在靠近釜顶、搅拌轴区域与釜底的“锥形区域”内易形成回流死区，造成物料堆积，应通过安装诱导锥、适当降低搅拌器的安装位置等方式减小回流死区，以提高搅拌器的混合效果。

参考文献

[1] Kroll N， Bieler H， Couaillier V， et al. ADIGMA-A European Initiative on the Development of Adaptive Higher-Order Variational Methods for Aerospace Applications： Results of a collaborative research project funded by the European Union，2006-2009[M]. Springer， 2010.

[2] Gnatowska R. A Study of Downwash Effects on Flow and Dispersion Processes around Buildings in Tandem Arrangement[J]. Polish Journal of Environmental Studies， 2015， 24（4）： 1571-1577.

[3] 刘志军. CFD技术在化工机械设计中的应用[J]. 化学工程与装备， 2020（2）： 187-188.

[4] 张云电， 董昌帅， 储瑞， 等. 反应釜内搅拌混合特性研究[J]. 机电工程， 2017， 34（10）： 1101-1105.

[5] 张慧敏， 廖辉良， 胡守明， 等. 单双层涡轮式搅拌器的流场分析与对比[J]. 中国农机化学报， 2016， 37（9）： 270-273.

[6] 周勇军， 袁名岳， 徐昊鹏， 等. 三叶后掠-HEDT组合桨搅拌釜内流场的模拟及实验[J]. 化工学报， 2019， 70（12）： 4599-4607.

[7] Luan D， Zhang S， Wei X，et al. Effect of the 6PBT stirrer eccentricity and off-bottom clearance on mixing of pseudoplastic fluid in a stirred tank[J]. Results in Physics， 2017（7）： 1079-1085.

[8] Zhang P， Chen G， Duan J， et al. Mixing characteristics in a vessel equipped with cylindrical stirrer[J]. Results in Physics， 2018（10）： 699-705.

[9] Jiang Z， Zhang L， Yao Q， et al. Agitator dependent homogeneity enhancement of co-precipitation reaction for improving the dispersibility of precursors and Y2O3 powders[J]. Ceramics International， 2017， 43（18）： 16121-16127.

[10] Li L， Xu B. Numerical simulation of hydro-dynamics in an uncovered unbaffled stirred tank[J]. Chemical Papers， 2017， 71（10）： 1863-1875.

[11] 莫惠珺， 范海濤， 王明玥， 等. 型式结构对双曲面搅拌器流场影响的数值模拟[J]. 环境工程学报， 2019， 13（5）： 1119-1127.

[12] 胡志梁， 于新海， 赖焕新. 拟塑性流体在六直叶搅拌器中的模拟与比较[J]. 华东理工大学学报（自然科学版）， 2019， 45（4）： 660-668.

[13] 张慧敏， 廖辉良， 胡守明， 等. 开启涡轮式搅拌器的流场分析及结构优化[J]. 中国农机化学报， 2016， 37（6）： 58-63.

[14] Sosnowski M， Krzywanski J， Gnatowska R， et al. Polyhedral meshing as an innovative approach to computational domain discretization of a cyclone in a fluidized bed CLC unit[J]. E3S Web of Conferences， 2017， 14： 01027.

[15] 王宁， 苏新兵， 马斌麟， 等. 网格类型对流场计算效率和收敛性的影响[J]. 空军工程大学学报（自然科学版）， 2018， 19（1）： 9-14.

[16] 王纯， 刘艳梅， 周涛， 等. 基于ICEM CFD对汽轮机末级三维叶片流场网格划分方法的优化[J]. 汽轮机技术， 2012， 54（5）： 324-326.

[17] 中华人民共和国国家标准： 有机产品： GB/T 19630.1-19630.4-2011 [S]. 北京： 中国标准出版社， 2012.

[18] Vakili M H， Esfahany M N. CFD analysis of turbulence in a baffled stirred tank， a three-compartment model[J]. Chemical Engineering Science， 2009， 64（2）： 351-362.

[19] 丁源， 王清. ANSYS ICEM CFD从入门到精通[M]. 北京： 清华大学出版社， 2013.

[20] 张晓东， 张培林， 傅建平， 等. 双方程湍流模型对制退机内流场计算的适用性分析[J]. 爆炸与冲击， 2011， 31（5）： 516-520.

[21] 纪兵兵. ANSYS ICEM CFD 网格划分技术实例详解[M]. 北京： 中国水利水电出版社， 2012.

[22] 刘国勇. 流体仿真与应用[M]. 北京： 冶金工业出版社， 2017： 24-25.

[23] 刘玉玲， 李东旭， 李盼盼， 等. 搅拌器内转轮半径对气液混合影响的数值模拟研究[J]. 水资源与水工程学报， 2017（2）： 14-18.

[24] Chen T， Wang L Q， Wu D Z， et al. Investigation of the mechanism of low-density particle and liquid mixing process in a stirred vessel[J]. The Canadian Journal of Chemical Engineering， 2012， 90（4）： 925-935.

[25] 武光霞. 涡轮式组合搅拌器流场模拟研究[D]. 青岛： 青岛科技大学， 2014.

[26] Ameur H， Ghenaim A. Mixing of Complex Fluids in a Cylindrical Tank by a Modified Anchor Impeller[J]. ChemistrySelect， 2018， 3（26）： 7472-7477.

[27] 付双成， 付飞， 巩建鸣， 等. 基于FLUENT搅拌釜底部回流区的数值模拟研究[J]. 石油机械， 2016， 44（8）： 102-107.

[28] 王学涛， 崔宝玉， 魏德洲， 等. 絮凝搅拌器内部流场特性数值模拟[J]. 东北大学学报（自然科学版）， 2018， 39（10）： 1442-1446.