基于SOM-MQE模型的设备故障预警方法

韩宝宏 闫明胜 段鹏飞 李志 张羽 朱慧敏

摘   要： 借助机器学习算法进行设备故障预警是保证设备安全可靠运行的有效手段，但故障数据样本难以获取，成为相关设备推广应用的一大挑战。构建一种结合自组织映射网络（SOM）和最小量化误差（MQE）的SOM-MQE模型，提出基于SOM-MQE模型的设备故障预警方法。首先，划分训练集和测试集，用训练集的设备正常状态数据训练SOM模型;然后，将实时数据与SOM所有图元中的权值矢量作比较，根据MQE值确定设备的故障预警区间，从而判断设备是否需要故障预警。采用某航空发动机的全生命周期数据进行实验验证，表明SOM-MQE模型在进行发动机故障预警时能达到74.81%的准确率，满足在缺少明确故障标签数据的条件下设备故障预警准确率不低于70%的行业要求。SOM-MQE模型易于构建，检测速度快，适用于大多数实际工业场景。

关键词： 自组织映射神经网络（SOM）;最小量化误差（MQE）;故障预警;航空发动机;权值矢量

引言

在实际工业生产中，小到一个标准件、大到发动机等复杂机械设备的寿命都是有限的，运行一段时间后就要维修（或者更换）。及时对设备进行故障预警，可以有效减少安全生产事故的发生。

目前，设备的故障诊断技术主要聚焦于信号分析和智能诊断两方面[1]。在信号分析方面[2]，故障诊断主要依赖相关从业人员具备的知识基础和经验;在智能诊断方面，故障诊断主要借助机器学习相关算法如支持向量机（Support Vector Machine，SVM）[3]、人工神经网络（Artificial Neural Network，ANN）[4]、核方法（Kernel Method）[5]和卷积神经网络（Convolutional Neural Network，CNN）[6]等的应用。这些方法在模式识别的过程中，需要借助大量的历史故障数据对模型参数进行拟合，但对于实际的工业场景来说，设备故障样本不像正常状态数据那样易于采集[7]，这对机器学习算法的推广应用提出了很大挑战。

自组织映射网络（Self Organizing Map，SOM）[8]是一种无监督的人工神经网络，其借鉴了人脑对信号进行处理的特点，依靠神经元之间的互相竞争，实现了神经网络的逐步优化。SOM算法结构简单、参数量少，所以被广泛用于语音识别[9]、聚类分析[10]、异常值剔除[11]等领域。文献[12]将SOM算法和免疫神经网络相结合，实现了飞机燃油系统的故障诊断，该方法在使用SOM算法进行数据处理的基础上，利用BP神经网络对故障进行分类，依然要求有充足的故障数据样本，具有一定的局限性。

为此，本文提出一种SOM和最小量化误差（Minimum Quantifying Error，MQE）相结合的模型，利用数据偏离正常特征空间的量化误差进行模式识别。首先，简要介绍SOM算法和MQE的基本原理;然后，提出基于SOM-MQE模型的设备故障预警方法;最后，将方法应用于某航空发动机的全生命周期数据，对设备故障预警有效性进行评估。

1  SOM算法和MQE

1.1  SOM算法原理

SOM算法可以对数据进行无监督学习（如聚类），其理论基础是神经网络对于某一图像或某种频率的特定模式产生的兴奋。SOM有输入层和输出层两层。输入层神经元的数量是由输入向量的维度决定的，一个神经元对应一个特征，各神经元通过权向量将外界信息汇集到输出层的各神经元;输出层中的一个节点代表一个需要聚成的类，输出层神经元的数量决定了最终模型的粒度与规模，这对最终模型的准确性与泛化能力有重要影响。

在本系统中，为了取得并分析航空发动机异常数据样本，需要对航空发动机的排气温度、总温度、燃油流量、滑油温度、振动值等进行全生命周期监测，将其全生命周期数据中前60%使用时长的数据作为正常数据，后10%使用时长的数据作为潜在异常数据。

SOM结构的区别主要在输出层，输出层节点的拓扑关系可以自定义。如果为一维模型，则输出节点依次连成一条线;如果为二维模型，则输出节点组成一个平面。图1所示为最常见的一维和二维SOM示意图。

SOM算法的基本思想接近于竞争神经网络，差别在于竞争神经网络中只有唯一获胜神经元才能调整权向量，其他神经元无权调整权向量;而在SOM中，获胜神经元对其邻近神经元的影响是由近及远，由兴奋逐渐变为抑制，即，不仅获胜神经元要训练调整权值，其周围的神经元也受到影响，要不同程度地调整权向量。具体调整过程是：以获胜神经元为中心设定一个邻域半径R，该邻域半径圈定的范围称为优胜邻域，优胜邻域初始状态较大;随着训练次数的增加，优胜邻域将不断收缩，直至半径为0。具体学习步骤如下：

（1）学习率初始化，建立初始优胜邻域，使用小随机数对输出层各神经元权重赋初值、归一化，得到;

（2）从训练集中随机选取一个输入样本并进行归一化处理，得到;

（3）遍历输出层中每一个节点，选取距离最小的节点作为优胜节点，即从与所有的内积中找到最大的;

（4）根據优胜邻域确定优胜邻域将包含的节点，并计算各自更新的幅度;

（5）更新优胜邻域内的所有神经元权重：

1.2  MQE

大多数情况下，故障数据非常难以准确采集，而正常状态数据往往可以方便且准确地获取，所以故障预警可以基于偏离正常特征空间的量化误差来进行。首先，用正常状态数据训练SOM模型;然后，将特征矢量与所有图元中的权值矢量作比较，若MQE超过了预设临界点，则表示可能已需要预警。借助于当前状态偏离正常运行基准模型的距离，可以设计新的故障预警指标，其做法是通过将新获取的状态监测数据输入到正常状态数据训练过的SOM网络，计算其MQE，并将该误差作为一种新的故障预警评估指标。MQE定义为

通过追踪MQE值，可以定量描述设备的健康状态。

2 基于SOM-MQE模型的设备故障预警

在训练集上训练模型，得到SOM-MQE模型设备预警故障的区间阈值。对于训练集中的每组设备，用正常状态数据训练SOM，然后将剩余数据与所有图元中的权值矢量作比较，计算其MQE。设备的故障预警区间设定为全生命周期寿命后10%节点的上下20%。计算该区间内的所有数据MQE的平均值，取的80%作为预警区间的下限，取的120%作为预警区间的上限。

在测试集上测试模型的有效性。在测试数据中，取每组设备的正常状态数据初始化SOM，然后将剩余被测数据与所有图元中的权值矢量作比较，计算其MQE。若MQE在区间内，则表示设备处于故障预警状态。

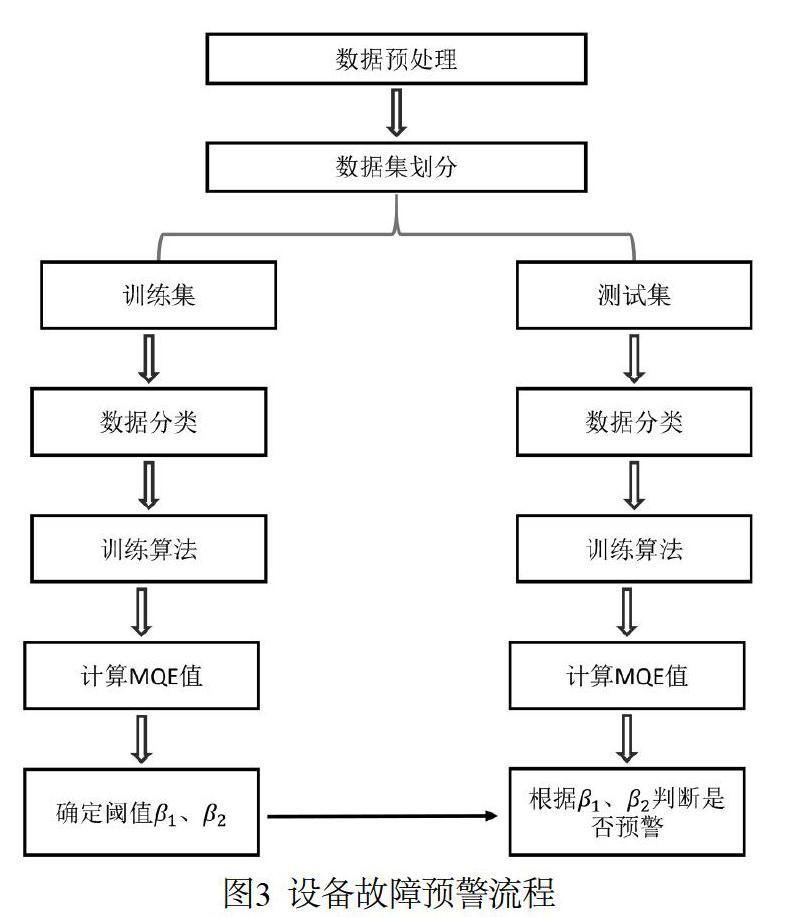
综上，设备故障预警的具体流程如下：

（1）划分训练集和测试集，将训练集和测试集中的每组数据划分为正常数据和故障数据，无故障数据标签设置为0，有故障数据标签设置为1;

（2）利用训练集的正常数据训练SOM模型;

（3）计算训练集数据中故障数据的MQE值;

（4）取故障预警数据MQE平均值的80%作为预警区间的下限，平均值的120%作为上限;

（5）利用测试集中正常数据初始化算法，计算每组数据剩余数据的MQE值，在区间内的为故障预警状态，其他数据为非故障预警状态;

（6）计算判断准确率，评估模型的性能。

设备故障预警流程图如图3所示。

3  实验与讨论

实验使用2008年预测与健康管理大赛所提供的数据集，其中包含218组类型相同的航空发动机的全生命周期数据。每一组数据反映了1台航空发动机从健康状态、衰退状态到故障（报废）状态的全过程。数据是多维的：第一维是设备代号;第二维是设备使用时长;第三维到第五维是对发动机有重大影响的操作设置;其他维度是传感器采集到的参数，如温度、压力等，但参数对应的物理含义没有明确解释。

在实验过程中，首先划分训练集与测试集：选择前100个发动机全生命周期数据作为训练集，后118个发动机全生命周期数据作为测试集;然后，归一化训练集中的传感器采集参数，确定训练集中发动机的最大使用时长为357个周期（每一个周期代表时长，竞赛未详细说明），假定此类航空发动机的额定使用时长是357个周期，不同的发动机由于出厂的差异和磨损程度的不同，剩余寿命也不同。根据发动机使用经验确定最大使用时长的前60%使用周期为正常数据，用于模型训练;确定最后10%使用周期作为预警节点，因为这段时间容易出现故障状态，要及时提醒对设备进行维修或者更换，以有效降低发动机的意外维修次数。为了减小误差，取10%节点上下限各20%求平均值，作为预警的时间节点区间。

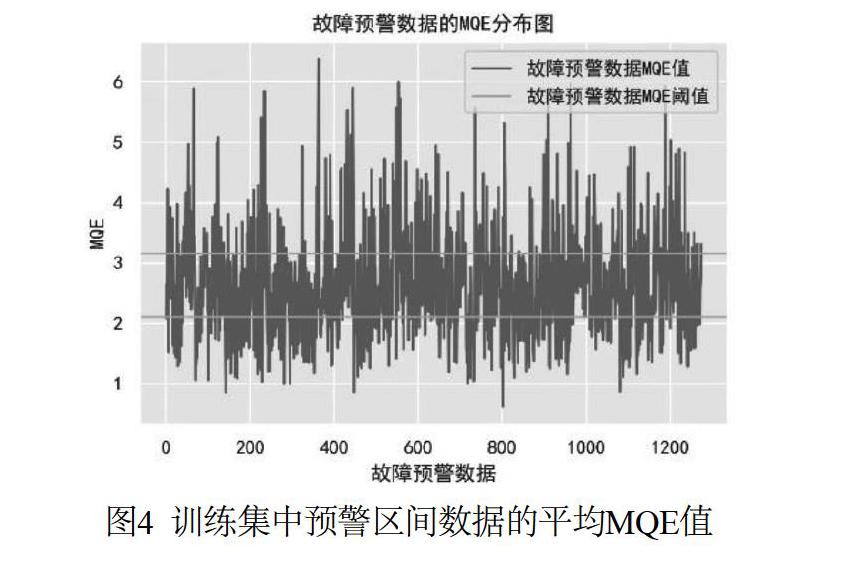
接下来，计算所有训练集中预警区间数据的平均MQE值（如图4所示），其结果为2.64，将其乘以0.8得到预警数据的下限为2.11，乘以1.2得到预警数据的上限为3.16。

对SOM-MQE模型进行测试。同样，先归一化测试集中的传感器采集参数;其次，将测试集中发动机最大使用时长的前60%使用周期作为正常数据训练SOM模型;模型训练完成后，使用测试集中每个发动机的剩余数据计算其与训练好的SOM模型的MQE值。

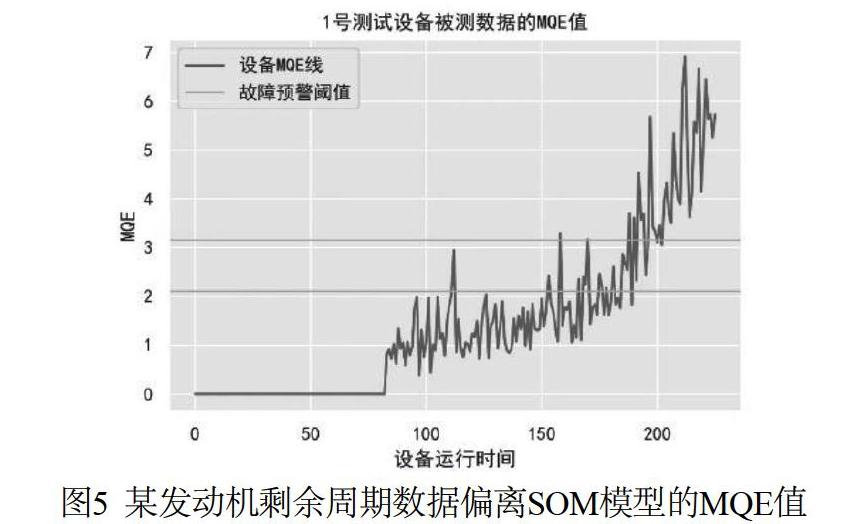
以测试集中的某个发动机（称为1号测试设备）为例，选择此发动机的前60%周期数据作为正常数据，用于初始化SOM模型，剩余周期数据用于验证。如图5所示，深色曲线为此发动机剩余周期数据偏离SOM模型的MQE值。可以看出，随着发动机运行时间的推移，MQE值不断变大，即设备越偏离正常状态，出现故障的风险越大。浅色水平线为根据训练集训练得到的故障预警阈值和，即当被测数据中MQE值在区间时，则认为设备处于故障预警状态。计算所有测试集数据中被测数据的MQE值，根据和判断设备状态，并输出预测结果，计算得到预警模型的准确率为74.81%，满足在缺少明确故障标签数据的条件下设备故障预警准确率不低于70%的工业界要求。

4  结论与展望

本文介绍了一种基于SOM-MQE模型的设备故障预警方法。该方法的优势在于，即使缺少明确的故障标签，也能够充分利用历史数据中的海量健康数据和使用经验构建基准模型，并基于观测数据与正常状态数据的偏差实时判定设备的健康状态，快速有效地对设备进行故障预警，降低意外故障导致的设备维修次数，在工业界具有显著的应用价值。

本文没有将设备中所有传感器采集的参数用作模型的输入。未来可考虑进行有效特征的选择和优化，简化模型输入，进一步提升算法的预测准确性。

参考文献

[1] El-Thalji I， Jantunen E. A summary of fault modelling and predictive health monitoring of rolling element bearings [J]. Mechanical Systems & Signal Processing， 2015， 60/61（1）： 252-272.

[2] 王江萍， 孫文莉. 基于小波包能量谱齿轮振动信号的分析与故障诊断[J]. 机械传动， 2011， 35（1）： 55-58.

[3] Thelaidjia T. A New approach of preprocessing with SVM optimization based on PSO for bearing fault diagnosis[C]// 13th International Conference on Hybrid Intelligent Systems （HIS）， 2013. IEEE， 2013.

[4] Moosavi S S， Djerdir A， Ait-Amirat Y， et al. ANN based fault diagnosis of permanent magnet synchronous motor under stator winding shorted turn [J]. Electric power systems research， 2015， 125（8）： 67-82.

[5] 李巍华， 史铁林， 杨叔子. 基于核函数估计的轉子故障诊断方法[J]. 机械工程学报， 2006， 42（9）： 76-82.

[6] Zhao D， Wang T， Chu F. Deep convolutional neural network based planet bearing fault classification [J]. Computers in Industry， 2019， 107： 59-66.

[7] 柯赟， 宋恩哲， 姚崇， 等. 船舶柴油机故障预测与健康管理技术综述[J]. 哈尔滨工程大学学报， 2020， 41（1）： 125-131.

[8] Kohonen T. The Self-organizing Maps [J]. Proceedings of the IEEE， 1990， 78（9）： 1464-1480.

[9] Xiao X， Dow E R， Eberhart R， et al. Gene clustering using self-organizing maps and particle swarm optimization[C]// Proceedings International Parallel and Distributed Processing Symposium. IEEE， 2003.

[10] 孙放， 胡光锐. SOM结合MLP的神经网络语音识别系统[J]. 数据采集与处理， 1996， 11（2）： 119-122.

[11] 路辉， 刘雅娴. 基于互相关分析和SOM神经网络的异常值检测平台[J]. 计算机测量与控制， 2018， 26（5）： 52-55.

[12] 戴敏， 祝加雄， 贺元骅. 基于SOM算法和免疫神经网络的飞机燃油系统故障诊断[J]. 计算机测量与控制， 2014， 22（11）： 3483-3486.