一种基于小波分析的卫星钟差数据粗差处理方法

王 威 许 芬 王宇谱

1 北京卫星导航中心，北京市北清路22号，100094 2 北方工业大学电气与控制工程学院，北京市晋元庄路5号，100144

卫星钟差数据能直接反映星载原子钟的工作状态，作为卫星导航系统不可或缺的一种数据产品，其质量的优劣对导航系统的性能至关重要。由于在轨卫星容易受外部环境变化等因素的影响，导致获取的卫星钟差数据经常出现间断、跳变和粗差等异常情况[1]，而含有异常数据的卫星钟差不仅会降低卫星钟性能分析的可靠性，还会导致钟差预报的精度随预报时长的增加快速衰减。由此可见，卫星钟差数据的预处理是原子钟稳定性分析、钟差预报等科学研究和工程应用的前提和基础。针对钟差数据的粗差探测与剔除等问题，较为常用的方法是中位数法(MAD)及其改进方法[1-5]。但MAD法参数的选取是基于经验值，若参数选取较大则粗差剔除得不够彻底；若参数选取过小，则部分有效数据会被当作粗差剔除。另外，还有其他的一些预处理方法[6-10]。

基于此，本文提出一种基于小波分析的数据预处理方法，能充分利用小波分析对数据局部特征的分辨能力，有效处理小量级的粗差值，同时顾及预处理后对钟差预报精度的影响，保证经过预处理后的数据能获得较高精度的预报参数。使用CODE解算的BDS卫星钟差数据进行数据预处理及拟合、预报，并与常用的MAD法进行对比分析，结果表明，新方法能够有效剔除数据中的异常值，得到较好的预处理数据，且基于新方法处理后的钟差数据能够有效提高卫星钟差预报的精度。

1 算法原理

小波分析理论具有较好的局部特征分辨能力，本文利用小波分析的优点，结合卫星钟差数据及其异常点的特性，给出一种基于小波分析的卫星钟差数据预处理方法。

1.1 基于小波分析的钟差数据预处理原理

利用小波分析进行粗差探测的主要依据在于数据序列中粗差点相较邻近数据有较大起伏，并且这些起伏的特征在不同尺度变换的小波系数中均有对应。因此，可以对数据进行小波分解，并通过处理小波系数的起伏情况进行粗差探测和剔除。

本文基于小波分析设计的卫星钟差数据粗差处理原理与过程见图1。

首先对钟差频率数据进行小波分解，得到低频小波系数cai和各层高频小波系数cdj，再对分解所得的低频、高频小波系数进行粗差处理。需要注意的是，在粗差处理过程中，对处理效果影响最大的因素是低频小波系数cai，因此采用低频小波的中位数作为阈值，即med=median{|cai|}，若cai>med/3，则将该点的小波系数设为粗差点[10]。对于高频小波系数cdj，利用σ=median{|cdj|/0.674 5}计算各层小波系数的方差，将|cdj|>3σ的小波系数点判定为粗差点。考虑到个别卫星的频率数据较为明显地偏离零值，若直接将粗差值置零，则置

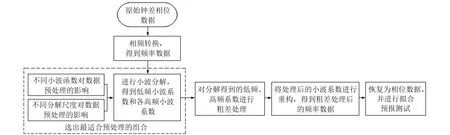
图1 数据处理流程Fig.1 Data process procedure

零点相当于成为了新的粗差值；若简单地将粗差值剔除，则会引起不必要的数据缺失。因此，本文使用三次分段样条方法对探测出的粗差点进行内插并替换，以减小对邻近数据的影响。将处理后的小波系数进行重构，获得粗差处理后的钟差频率数据，同时利用参数为5的MAD法对原始频率数据进行剔除粗差处理，分别将2种粗差预处理后的频率数据恢复为相位数据，并进行拟合与预报，对比分析二者的差异。

1.2 小波函数与分解尺度的选型

利用小波函数进行钟差数据预处理时，可选用多种小波函数，常用的有db系、sym系和coif系，每种小波函数又可搭配多种分解尺度。因此，卫星钟差数据预处理的效果同时受小波函数和分解尺度两个因素的影响，选取最适合处理卫星钟差数据的小波函数和分解尺度对数据的拟合预报至关重要。文献[3]和[10]分析了不同小波函数处理BDS钟差数据的差异，认为db系小波的处理精度要高于sym系和coif系小波，因此，本文选用分解尺度为2、3、4、5、6的dbN(N=2,3,4,5,6,7,8,9,10)小波分别处理卫星钟差。考虑到C10卫星的数据相对完整连续，此处对该卫星的数据进行预处理(选用其他卫星亦可)，并利用二次多项式模型对数据进行拟合，统计拟合残差的RMS值，随后利用二次多项式模型对数据进行2 h预报，统计预报残差的RMS值。

图2中纵轴表示不同小波函数的拟合预报精度，横轴表示不同分解尺度的拟合预报精度，其中蓝色越深表示拟合或预报精度越高，红色越深表示精度越低。对于同一分解尺度而言，不同小波处理的拟合精度相当(除分解尺度5的db10小波函数拟合精度较差及分解尺度6的db5～10小波外)，大部分小波函数经过分解尺度6的小波分解处理后拟合精度不高，其原因是当分解尺度越大时，低频小波系数分解得到的信息越少，导致重构后的数据存在失真。对于同一小波函数而言，随着分解尺度的增加，拟合残差整体呈逐渐变小的趋势，其原因是当分解尺度增大后，对数据去噪和平滑的效果更为明显，处理后数据的高频噪声被显著消除，离散程度变小，其拟合残差也相应变小。拟合精度最高的组合是分解尺度6的db3小波函数。对于预报而言，分解尺度为2、3、4的各小波均有较高的预报精度，其中分解尺度3的小波预报精度整体较高。另外，在分解尺度大于4的情况下，预报精度反而出现衰减。从同一小波函数来看，各小波函数在分解尺度小于4时，均有较好的预报精度。从整体来看，db2、db3、db4小波的预报结果较好。

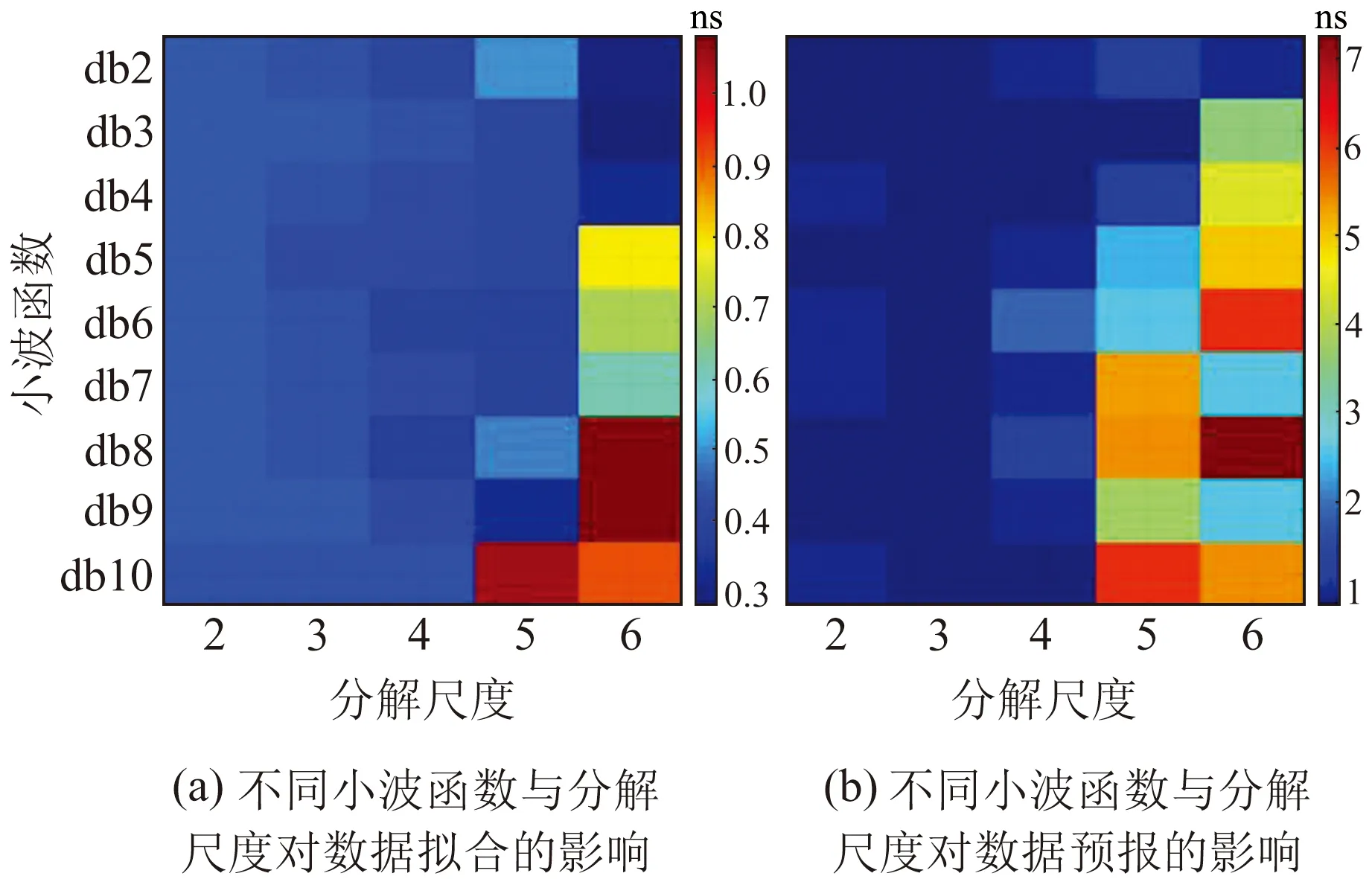
图2 不同小波函数和分解尺度各层小波系数及粗差剔除情况Fig.2 Wavelet coefficients and gross error elimination at different wavelet and decomposition scales

1.3 不同分解尺度处理钟差数据的差异分析

基于小波分析的数据预处理受所选小波函数及分解尺度的影响，其中分解尺度对预处理的影响更为显著，因此应着重对分解尺度的影响展开分析。

图3 尺度2的小波分解后的各层小波系数及粗差剔除情况Fig.3 Wavelet coefficients and gross error elimination of each layer after 2td dimension wavelet decomposition

图4 尺度3的小波分解后的各层小波系数及粗差剔除情况Fig.4 Wavelet coefficients and gross error elimination of each layer after 3th dimension wavelet decomposition

图3和4分别为C09卫星钟差频率数据经过db3小波用分解尺度2和3进行分解后各层小波系数及粗差剔除情况。可以清晰地看到，数据中存在粗差值，且在各层高频小波系数中能明显观察到系数发生跳变。用尺度2分解后，在低频小波系数中也能明显观察到粗差点；而用尺度3分解后，低频小波系数无明显的粗差点，与§1.2关于分解尺度越大低频小波系数分解得到的信息越少的分析结论相互印证。因此，选择合适尺度进行分解对粗差剔除的效果有直接的影响。经过处理，各层小波系数的跳变值被剔除，通过小波重构则可得到剔除粗差后的钟差频率数据。

1.4 两种数据预处理方法的差异分析

为比较本文提出的数据预处理方法和MAD法在粗差探测方面的差异，选用分解尺度3的db3小波函数作为小波分析的数据预处理方法，并与参数为5的MAD法进行对比，通过人工判读的方式评估粗差探测的效果。

图5(a)反映的是包含粗差的原始钟差频率，图5(b)和5(c)分别为通过MAD法和小波分析预处理后的频率数据。MAD法和小波分析均能有效地剔除粗差数据，说明小波分析处理粗差值具有合理性。对比MAD法和分解尺度3小波函数的处理结果可以看到，经参数为5的MAD法处理后，较大的粗差值被有效探测并剔除，但仍存有一部分较小的频率跳变值未能被探测到；而使用小波分析处理后，部分高频噪声被消除，量级较小的粗差值会随着高频噪声的消除被一并剔除。从粗差探测与剔除效果来看，本文方法处理后的数据比MAD法更为集中和平滑。选用分解尺度较大的小波则集中程度更为明显，这在一定程度上改变了原始钟差数据，对于评估卫星钟的性能而言，势必会降低评估结果的客观性，但对于钟差预报而言，则有利于参数的估计。由于卫星钟差数据在导航定位的应用中是需要进行预报的，因此预报精度的提升对于导航定位有着十分实用的价值。据此，本文设计了一套基于钟差预报的量化实验，将MAD法和小波分析处理后的频率数据恢复为相位数据，并对该数据进行拟合与预报，对比分析2种预处理方法的预报精度。

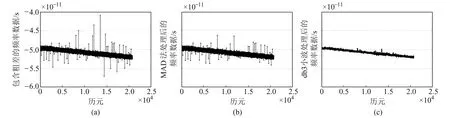
图5 MAD法与小波分析预处理后的对比Fig.5 Comparison between MAD method and wavelet analysis

通过对小波函数与分解尺度的选型进行分析发现，选用分解尺度3或4的db3小波函数进行预处理能获得较好的结果。因此，本文在随后的实验中统一使用分解尺度3的db3小波函数。

2 实验分析

本文使用2018-02-01～02-10共10 d的CODE解算的BDS卫星钟差相位数据(ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex/)，数据采样间隔为300 s。

2.1 数据拟合情况对比

利用小波分析对CODE解算的BDS各颗卫星的钟差数据进行预处理，分别比较各颗卫星数据跨度为24 h、48 h和72 h的拟合精度。

由图6可知，尺度3的db3小波分解和MAD法预处理后数据的拟合精度相当，并且拟合残差随着数据跨度的增加而变大。分析其原因，一方面是由于多星定轨解算的钟差存在跨天跳变，导致跨度较长的数据存在不连续的情况，影响拟合残差的统计结果；另一方面，跨度较长的数据包含变频和跳相的可能性会增加，最终影响拟合精度。

图6 db3小波处理不同数据跨度的拟合情况Fig.6 Fitting residuals of db3 wavelet preprocess with different data spans

2.2 数据预报情况对比

分别统计使用小波分析和MAD法预处理的拟合资料跨度为24 h、48 h和72 h的数据2 h的预报精度，并比对2种方法以24 h拟合资料分别预报2 h、4 h、6 h和12 h的预报精度。为了更集中、综合地评价MAD法和基于小波分析的数据预处理方法在钟差数据预报方面的效果，对计算结果进行算术平均，得到的预报精度不是比较某颗卫星的预报效果，而是比较2种预处理方法的效果。

表1统计了2种预处理方法在拟合资料长度不同的情况下2 h的预报精度对比，可以看出，2种预处理方法2 h的预报精度均优于2 ns，基于小波分析的预处理方法得到的数据在钟差预报方面要优于MAD法，预报精度至少提高10%。表2统计了2种预处理方法在拟合资料长度相同的情况下不同时长的预报精度的对比，可以看出，预报精度随预报时长的增加而增大，基于小波分析预处理方法的预报精度比MAD法有提升，但提升幅度随预报时长的增加而降低。

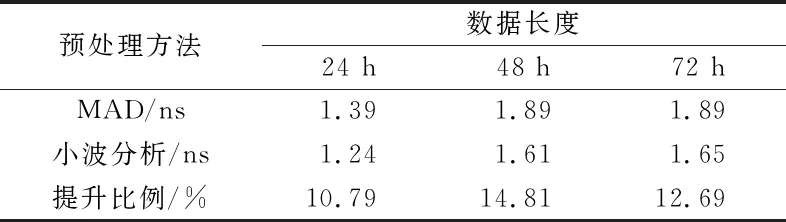
表1 2种预处理方法在不同数据长度时的预报精度对比

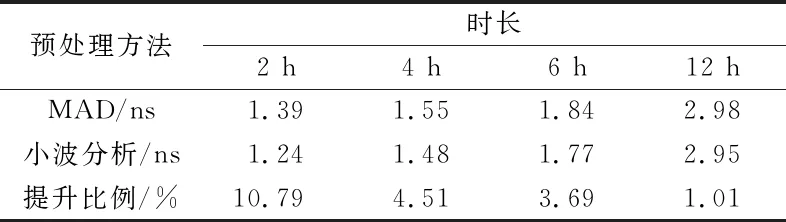
表2 2种预处理方法的不同时长的预报精度对比

3 结 语

本文提出一种基于小波分析的卫星钟差数据预处理方法，通过合理设置各层小波系数的异常数据剔除阈值，可有效剔除数据中的粗差点。分析使用不同分解尺度、不同小波函数对粗差处理的影响后发现，分解尺度3和4的db3小波函数最适合进行粗差处理。另外，本文还进行了不同数据跨度的拟合精度及预报精度分析，从结果上看，拟合精度随分解尺度的增大而逐渐提高。对比MAD法，小波分析的预处理方法在2 h短期预报方面有较大优势，精度提升超过10%。