水体透射光谱的多特征融合COD含量估算研究
2021-06-08王彩玲张育春王静怡
王彩玲,张育春,王静怡
(西安石油大学 计算机学院,陕西 西安 710065)
引言
化学需氧量(chemical oxygen demand,COD)在生活污水、地表水等的检测中占据重要地位,能够很好地反映水污染的程度[1]。传统的COD检测方法是重铬酸钾法或高锰酸钾法,两种方法都存在耗时长、人力物力消耗较大、操作不便且难以实现大批量快速检测的问题[2],而要更好地实现水污染的防治,就必须以大面积水质状况检测为前提和基础。
高光谱检测技术具有绿色、高效、耗时较少等优点,因而不少学者结合偏最小二乘法进行水质检测技术的研究。RYAN等人构建出偏最小二乘最佳高光谱Chl-a浓度估算模型[3];ALI等人利用高光谱技术检测出水体总悬浮固体浓度[4];曹引等人建立偏最小二乘水体浊度高光谱反演模型,为水体浊度大面积遥感检测提供了技术支持[5];张贤龙等人提出高光谱技术水质参数浓度反演模型[6];蔡建楠等人采用GA遗传算法实现了基于偏最小二乘法高光谱COD检测模型的优化[7]。近年来,BP(back propagation)神经网络模型在非线性映射能力以及网络结构上的优势被应用到数据检测领域[8],但对于水质检测研究较少。因此结合BP神经网络研究基于高光谱技术的COD含量检测,具有很好的理论研究意义和实践价值。
本文以水体COD含量为研究对象,通过多种预处理方法对高光谱技术采集的数据进行处理和特征提取,并进行多特征融合,建立BP神经网络水体COD含量估算模型。经实验对比,基于多特征融合BP神经网络模型的决定系数高达0.991 64,均方根误差为0.030 9,模型性能最优,能够实现水体中COD含量的检测。
1 实验数据
本次实验所用仪器为OCEAN-HDX-XR微型光纤光谱仪,光谱范围200 nm~1 030 nm,选择配比溶液为1 mg/L、2 mg/L、3 mg/L、4 mg/L、5 mg/L、6 mg/L、7 mg/L、8 mg/L、9 mg/L、10 mg/L的COD标液,相同时间间隔重复采集上述标液的高光谱数据,共计100条,随机打乱划分为校正集与验证集,其中校正集90条,用于模型的训练;验证集10条,用于模型性能的验证。通过白板校正得到所采集高光谱数据的光谱透射率值[9],如(1)式所示:

式中:RO为原始光谱数据;RW为白板数据。
2 实验结果
2.1 数据处理
采集到的光谱信息夹杂各类噪声,因此我们选择做平滑处理以降低噪音的干扰。本次实验选用滑动平均滤波器进行平滑去噪。图1为某一光谱透射率数据的原始及其平滑曲线图。
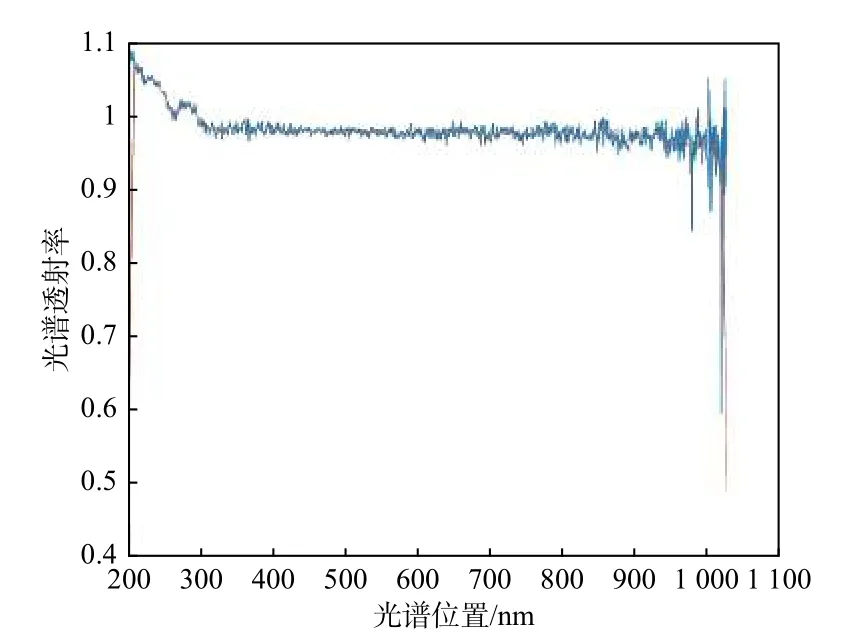
图1 原始数据及平滑光谱曲线Fig.1 Original data and smooth spectrum curve
分别采用不同的预处理方法进行处理。其中,采用双向二阶导数去除背景信号,提高光谱数据的分辨率[10];采用多元散射校正有效消除由于散射水平不同会给光谱数据带来差异,增强光谱与数据之间的相关性[11];采用标准正态变量变换降低固体颗粒大小、表面散射以及光源变换等对光谱信息的影响[12]。
2.2 特征波段的提取
采用偏最小二乘回归分析分别对上述特征做特征提取,计算最佳主成分的个数,对最佳主成分数进行筛选。回归系数图如图2所示。
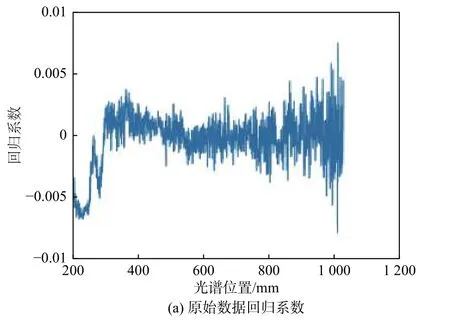
由图2可知,COD原始数据敏感波段大体分布于500 nm~800 nm,提取特征波段150个。双向二阶导数敏感波段分布在400 nm~900 nm之间,提取特征波段33个;多元散射校正以及标准正态变量变换敏感波段都分布在200 nm~300 nm之间,分别提取特征波段48个。
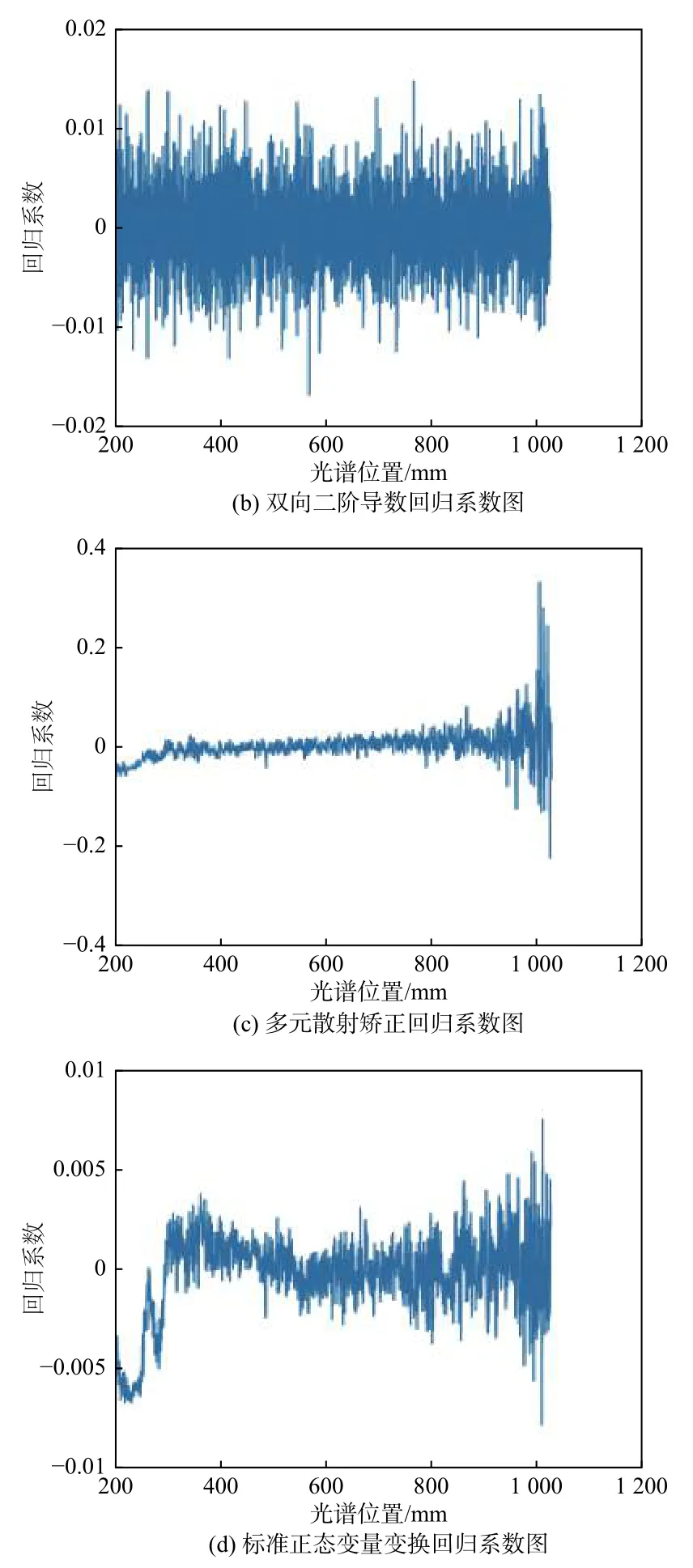
图2 回归系数图Fig.2 Regression coefficient diagram
2.3 模型的建立
本文采用BP神经网络方法以上述特征波段为自变量,将不同浓度的COD样本的浓度与光谱数据进行拟合,通过对样本数据进行训练,分别建立基于各类自变量的BP神经网络特征模型,检测结果如图3所示。
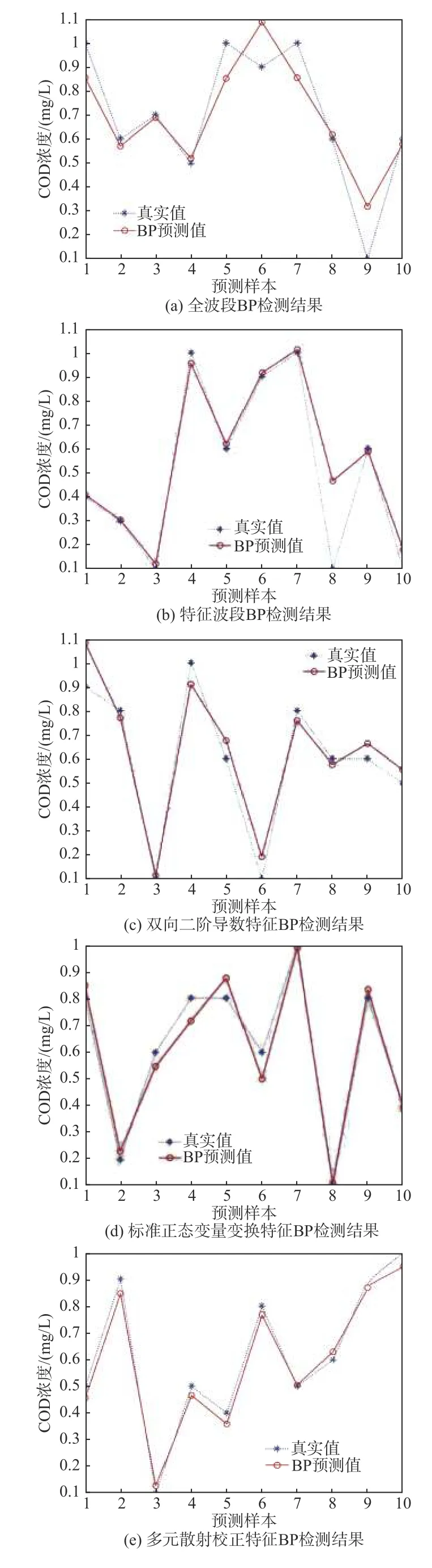
图3 模型检测结果Fig.3 Testing results of model
以均方根误差RMSE和决定系数R2以及测试时间3个参数为标准对所建立的各个模型进行精度检验与比较。其中:均方根误差越小,说明模型选择和拟合更好;R2越接近模型1的拟合效果越好。
检验结果如表1所示。

表1 模型精度检验结果Table 1 Testing results of model accuracy
由表1可知,特征波段BP神经网络的训练时间由365.873 s降低为3.386 003 s,测试时间降低为0.202 852 s,极大地减少了计算量,缩短了模型建立以及检测时间,且误差更小,拟合优度更高,性能有了很大的提升,说明特征波段提取可以实现水体中COD含量检测的优化。经过预处理之后,双向二阶导数特征BP神经网络R2为0.967 58,均方根误差与原始特征波段结果较为接近;标准正态变量变换特征BP神经网络,其R2高达0.979 02,均方根误差较低;多元散射校正特征BP神经网络模型R2达到0.990 49,RMSE为0.037 6,模型性能均高于特征波段模型,说明3种优化处理对于提高模型的精度均有效。
2.4 多特征融合BP神经网络模型的建立
为了提升模型检测的精度,学者利用多种方式对提取的特征进行优化,其中,特征融合是一项常用策略[13]。不同预处理方式所提取的不同特征向量反映的特性不同,对其进行优化组合,可以在保留有效鉴别信息的基础上消除冗余信息,从而提高模型的精度。
本文采用典型相关分析方法将3种特征进行融合,以交叉验证误差均方根RMSECV为评价标准[14],筛选80个波段进行多特征融合BP神经网络模型的建立,并采用目前较为成熟的偏最小二乘模型[15]进行对比。图4为对应的检测结果。
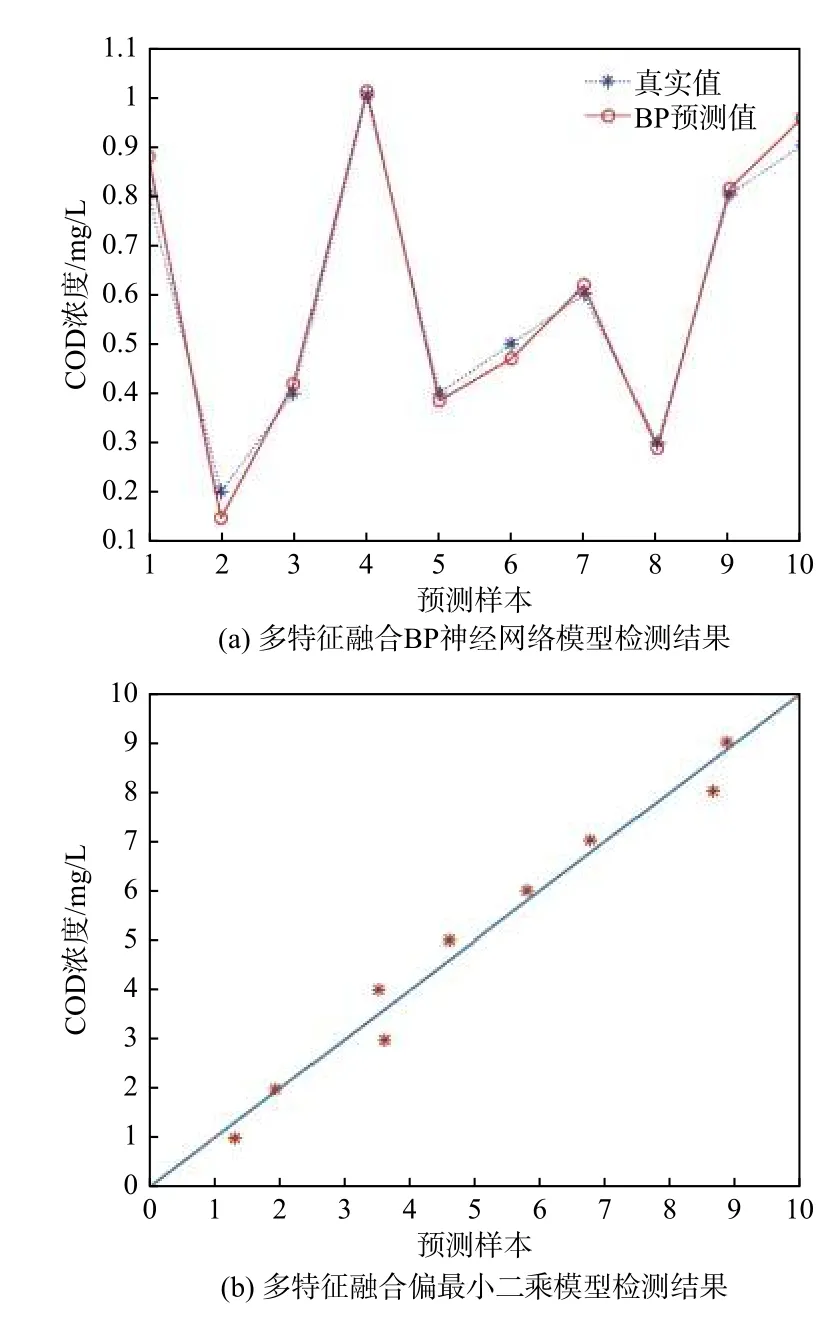
图4 多特征融合模型检测结果Fig.4 Testing results of multi-feature fusion model
2.5 最优模型筛选
对多特征融合BP神经网络模型以及多特征融合偏最小二乘模型进行精度对比。检验结果如表2所示。
从表2可知,特征融合BP神经网络模型R2高达0.991 64,RMSE为0.030 9,模型拟合度以及精度均有提高,且高于偏最小二乘法预测模型。根据R2最大、RMSE最小原则,最终采用多特征融合BP神经网络模型进行水体COD含量的检测。
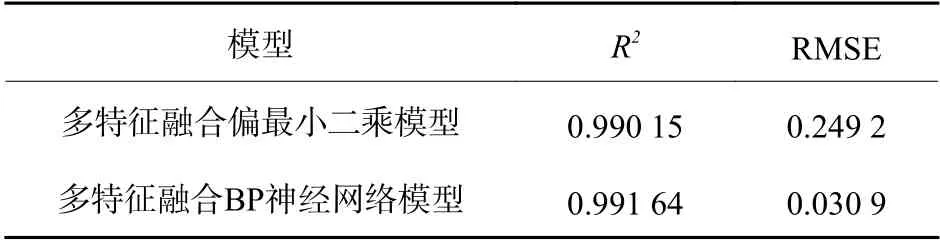
表2 模型精度检验结果Table 2 Testing results of model accuracy
3 结论
本文对光谱透射率数据进行预处理,采用偏最小二乘回归系数法提取特征波段,建立BP神经网络全波段模型、特征波段模型以及多特征融合模型,分析不同特征输入对模型精度的影响,结果表明:3种预处理方法可以有效降低噪音的干扰;偏最小二乘回归系数法可以有效降低数据维度,同时可筛选出相关性较好的波段,COD估算模型的精度;多特征融合BP神经网络模型决定系数达到了0.991 64,均方根误差为0.030 9,依据R2最大、RMSE最小原则,采用基于多特征融合的BP神经网络模型可以建立精度较好的COD定量估算模型。
