基于Weibull分布的非均质性对花岗岩声发射与能量影响的离散元模拟

沈琴冰

(广东粤源工程咨询有限公司，广州 510600)

1 概 述

岩石是天然产出的、由一种或多种矿物或其他物质构成的固态集合体。力学性质的非均质性是岩石基本的性质之一，岩石内部各种矿物成分均对岩石材料的宏观力学性质有重要的影响[1]。岩石内部矿物组成成分的非均质性是造成岩石在外荷载下表现出宏观力学性质离散性的原因之一[2]。

岩石的非均质性控制在岩石的宏观力学响应，到目前为止，C.A.Tang等[3]对岩石的非均质性对岩石强度与变形特性的影响进行了大量的研究。结果表明，非均质性对于岩石强度的最大影响在于非均质性会引起加载过程中岩石内部的局部应力集中现象，从而使得岩石力学性质的弱化和破坏的快速进行[4]。由于在室内试验中难以准确测量岩石的非均质性，因此目前研究岩石的非均质性的方法主要为数值模拟。宏观力学参数的统计规律较为符合Weibull分布，因此许多学者将岩石的力学参数假定服从Weibull分布，以此来研究力学参数的非均质性对岩石强度的影响。如RFPA软件中岩石单元的力学参数可以设置为服从Weibull分布，研究表明，非均质性对裂纹扩展和强度产生很大影响[3,5]。罗荣等[6-8]采用细胞元数值模拟方法研究了Weibull分布对于模拟多矿物组成的岩石的适用性，研究表明非均质岩石的力学特性由细胞单元力学特性和其非均质特性共同决定。

采用数字图像处理技术，可以将岩石彩色照片识别出不同矿物组分的具体位置，从而可以基于真实岩石图像建立非均质模型，实现细观尺度的非均质岩石模型建模。如岳中琦等[9-10]、于庆磊等[11]以及李国莹[12]等均通过对组成岩石模型的不同单元赋予不同的力学参数来定量模拟岩石的力学性质的非均质性。

花岗岩作为一种良好的建筑材料，具有优越的力学性能。花岗岩主要由斜长石、黑云母、石英等矿物成分组成。不同矿物成分之间的力学性质差别巨大，例如黑云母单轴压缩强度很小，而石英单轴压缩强度较高。因此，造成了花岗岩力学性质的非均质性。而PFC软件[13]在研究花岗岩的力学性质方面表现出良好的性能，由于PFC软件属于微细观建模，非常适于花岗岩的非均质性研究。本文通过北山花岗岩的室内试验数据[14]进行对比，验证本文所建模型的正确性。然后通过PFC2D中微观参数服从Weibull分布，从而研究花岗岩力学参数的非均质性对岩石声发射和能量的影响。

2 基于Weibull分布的非均质模型的建立

基于Weibull分布的力学参数赋值方法是数值模拟当中表征岩石材料非均质性时最广泛的方法[6]。本文将PFC2D中的4个微观参数(颗粒接触模量、平行黏结模量、平行黏结抗拉强度和平行黏结黏聚力，具体数值见表1)服从Weibull分布，以此研究Weibull分布中形状参数m对岩石声发射和能量演化的影响。

接下来以平行黏结抗拉强度为150 MPa时，介绍PFC2D中如何实现微观参数非均质赋值。Weibull分布的概率密度函数表达式和累积分布函数表达式为：

(1)

F(σt)=1-e-(x/σt0)mx>0

(2)

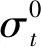
采用Monte-Carlo法生成随机变量：

(3)

式中：R为(0,1]之间的均匀分布。

本文中，m取值分别为2、4、6、10。平行黏结抗拉强度为150 MPa时，平行黏结抗拉强度的概率密度函数图见图1。本文所建立的模型宽50 mm，高100 mm，高宽比为2，与室内实验[14]保持一致。在PFC2D中显示见图2。

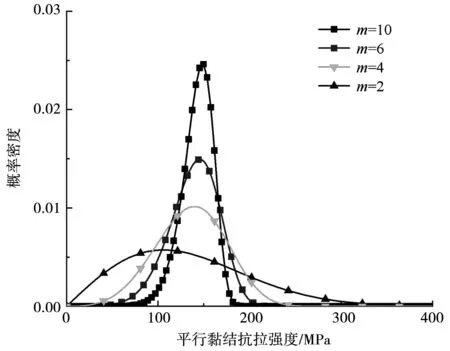
图1 平行黏结抗拉强度概率密度图

图2 平行黏结抗拉强度数值分布 (图中数值单位为Pa)

PFC2D中一般通过“试错法”不断调整微观参数，使得所建立的非均质模型的宏观力学性质和室内实验中花岗岩宏观力学性质基本一致。

首先通过均质模型标定微观参数，即同一参数不同平行黏结接触取同一值。最终选取的微观参数见表1。宏观力学性质对比见表2。表2证明本文所取微观参数基本可以反映室内实验中花岗岩的宏观力学性质。

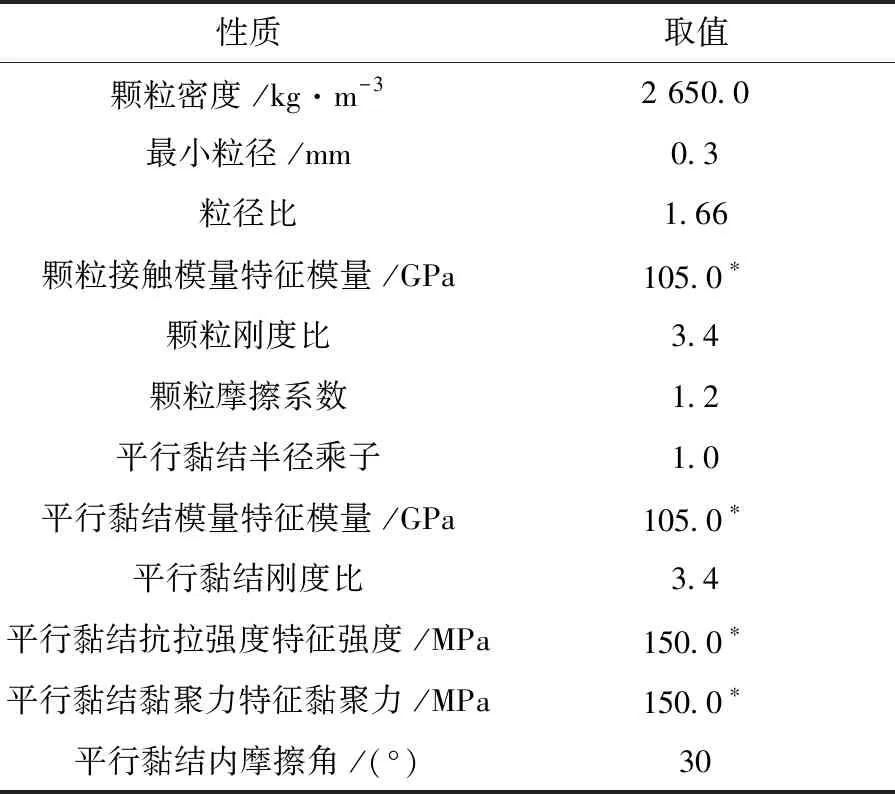
表1 PFC微观参数表

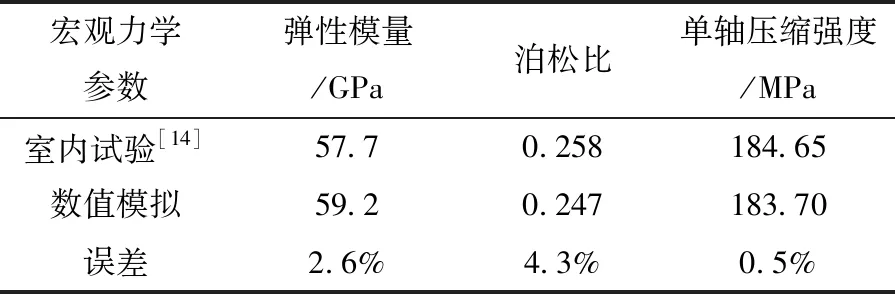
表2 宏观力学性质对比表

接下来，采用Weibull分布随机赋值的方法，将形状参数m设置为2、4、6、10，特征参数见表1，研究力学参数的非均质性对岩石声发射和能量演化的影响规律。

3 结果分析

3.1 应力-应变曲线

本文所建立的5个模型(均质模型、m=2、m=4、m=6、m=10)的应力-应变曲线见图3。宏观力学性质(弹性模量、单轴压缩强度和泊松比)见图4。

图3 应力-应变曲线

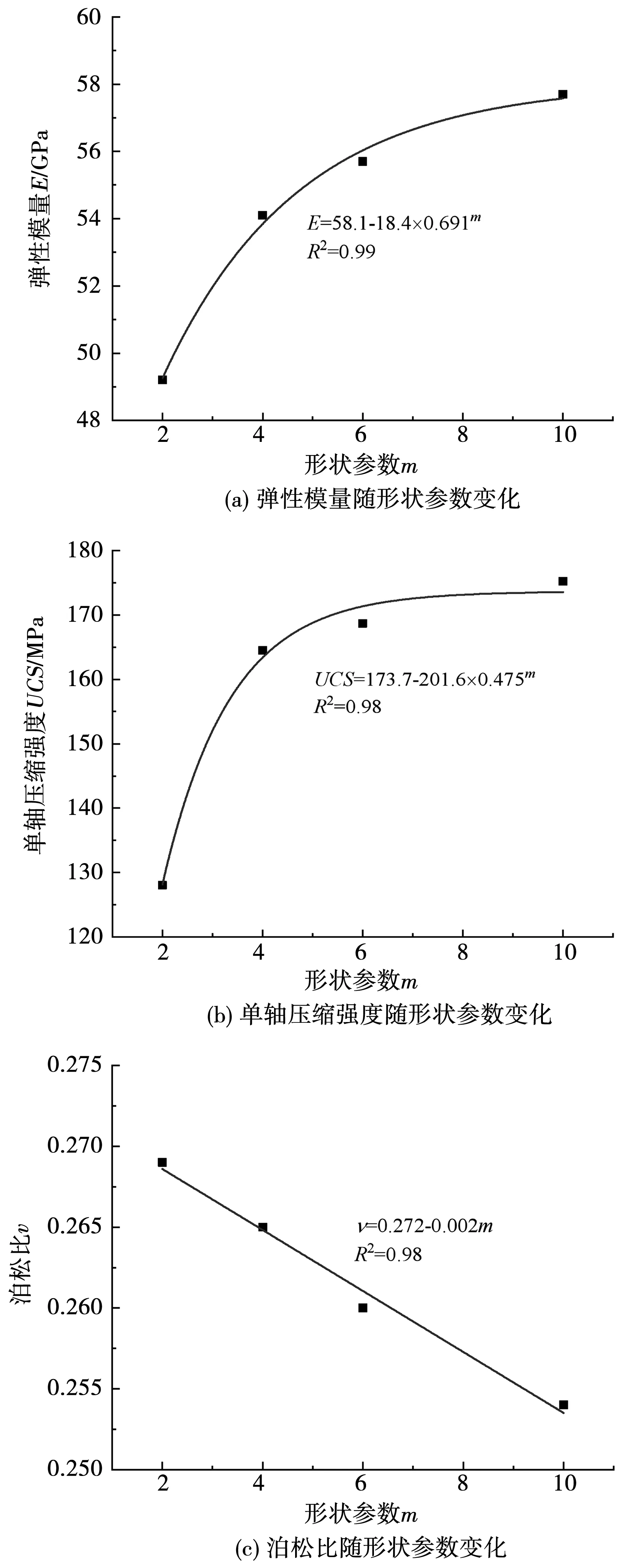
图4 宏观力学性质随形状参数变化图

由图3、图4可知，力学参数的非均质性对岩石的宏观力学响应影响非常大。随着形状参数m的增加，模型非均质性减弱，模型的力学性质越来越均一化，使得模型的单轴压缩强度逐渐增加。当m=10时，单轴压缩强度较均质模型减小4.6%，弹性模量减小2.5%，而泊松比增加2.8%。弹性模量和单轴压缩强度随形状参数拟合成指数函数关系，泊松比随形状参数拟合成线性函数关系。

3.2 声发射特征分析

在室内实验中，花岗岩内部的矿物颗粒及其胶结物在加载过程中会发生破裂而释放能量，产生声发射事件。在PFC2D模拟中，通过颗粒间接触断裂来模拟声发射事件[15-18]。图5为单轴压缩下每20个时步内声发射数(接触断裂数)与应变关系曲线。

由图5可知，5个模型声发射特征基本类似，大致可以分为4个阶段：初始压密阶段、弹性阶段、峰前塑性阶段和峰后破坏阶段。在加载初期，声发射数较少(图5(b))或者基本没有(图5(a)、图5(e))；随着加载的进行，轴向应力-轴向应变曲线进入弹性阶段，声发射数逐渐增加，

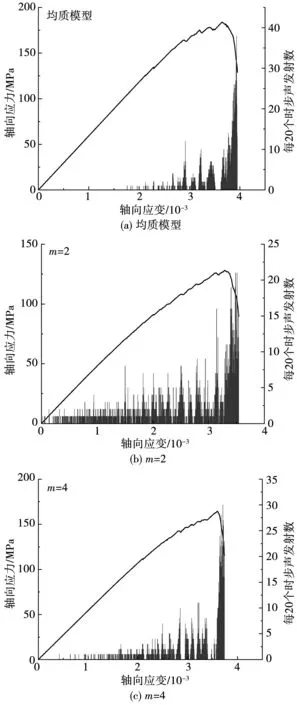
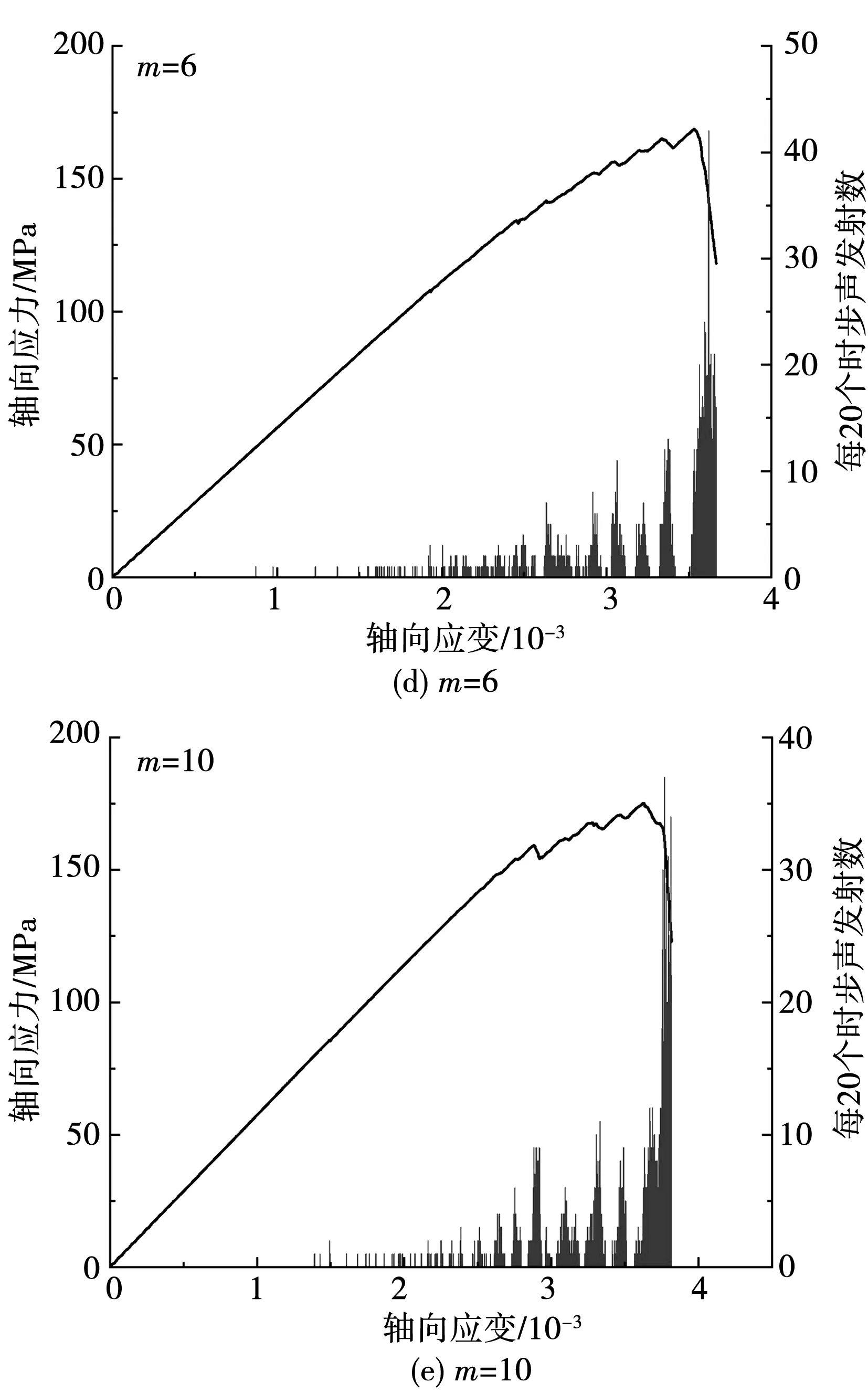
图5 声发射、应力-应变关系

但是整体依然较少；到达峰前塑性变形阶段，声发射数突然增加，表明模型发生大量损伤，即将到达峰值强度点；峰值强度点至峰后破坏阶段，声发射数达到顶峰，表明模型形成大量宏观可见的贯通裂纹，模型已经失去承载能力。

从图5可知，非均质度对声发射特征有一定的影响。其中最明显的区别就是当形状参数小(模型非均质度高，模型力学参数分布不均匀)的时候，初始压密阶段会随机产生一定量的声发射信号；而当形状参数大的时候，初始压密阶段则基本没有声发射信号。原因是因为当模型力学参数分布不均匀的时候，少数接触力学强度很小，在加载初期就会发生破裂。因此，可以认为相较于均质模型(图5(a))，采用Weibull分布赋值的模型(图5(b)-图5(e))产生了一定初始损伤。

3.3 能量演化特征分析

在PFC2D中，可以测量出模型在加载过程中各种能量的变化[19]。总应变能为颗粒黏结能和应变能之和，研究证明，从PFC2D中细观力学的角度研究能量演化特征极具优势[20]。根据能量守恒定律，定义耗散能=边界能-总应变能。不同种类的能量(边界能、动能、耗散能、摩擦能、总应变能)随形状参数变化关系见图6。

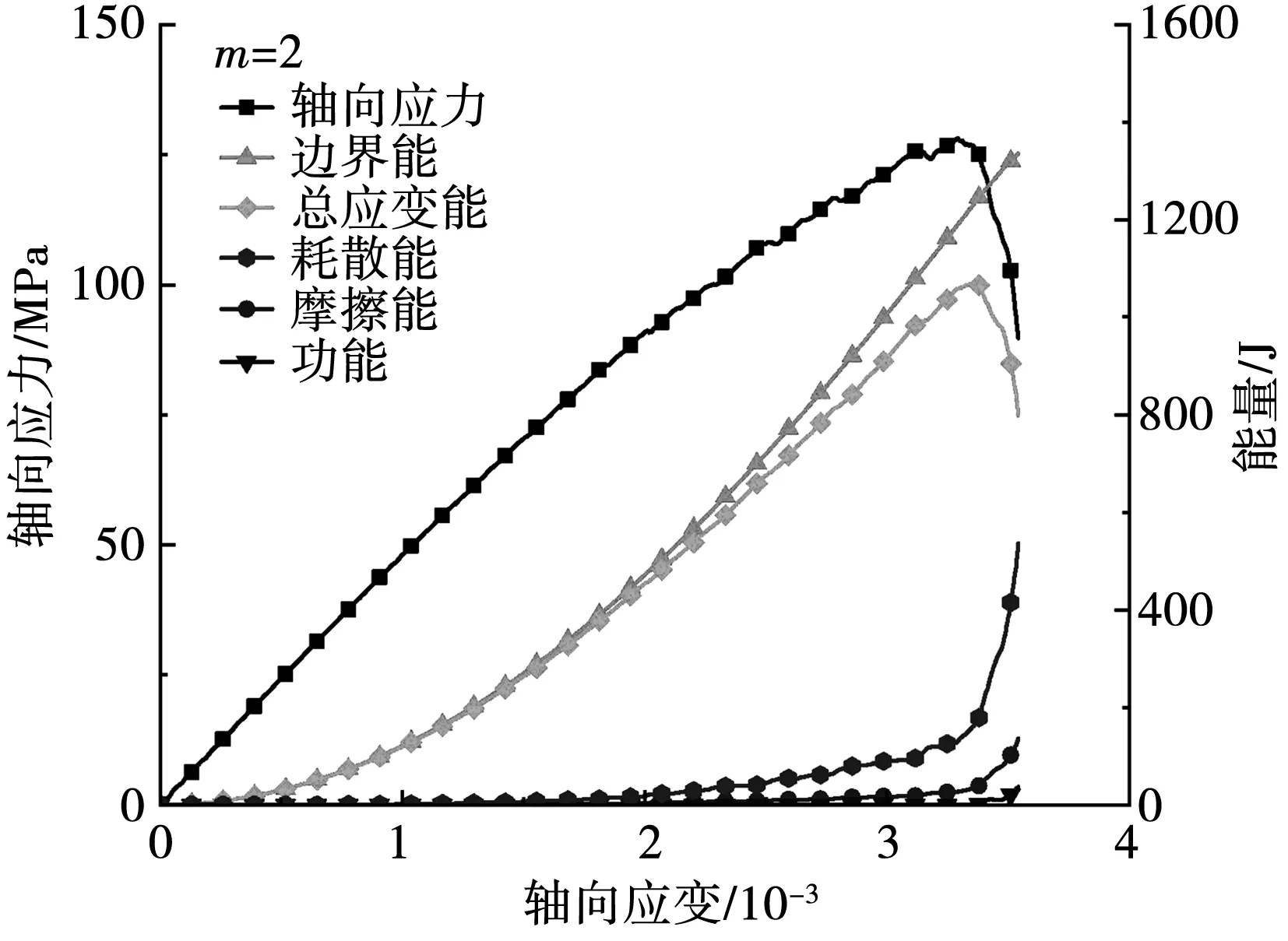
图6 形状参数为2时能量变化

由图6可知，随着加载的进行，外界输入模型的边界能逐渐增加，但是由于初期模型无裂纹产生，边界能全部转化成模型的应变能， 而耗散能、动能和摩擦能都基本为0。在弹性阶段，微裂纹逐渐萌生，裂纹扩展所消耗的能量逐渐增加，到达峰前塑性阶段时，耗散能急剧增加，表示模型微裂纹数量急剧增加，对应图5中峰前塑性阶段声发射数猛增。此时，颗粒之间相互滑移，导致模型摩擦能和颗粒动能也迅速增加。轴向应力到达峰值强度时，总应变能也几乎同步到达峰值，然后模型破坏失效，总应变能迅速释放，耗散能持续增加。在整个模型加载过程中，颗粒动能占系统能量比例很小；总应变能随轴向应变先不断增加，后减小；耗散能不断增加，且占系统能量比例不断增加。

非均质性对系统能量演化的影响见图7。

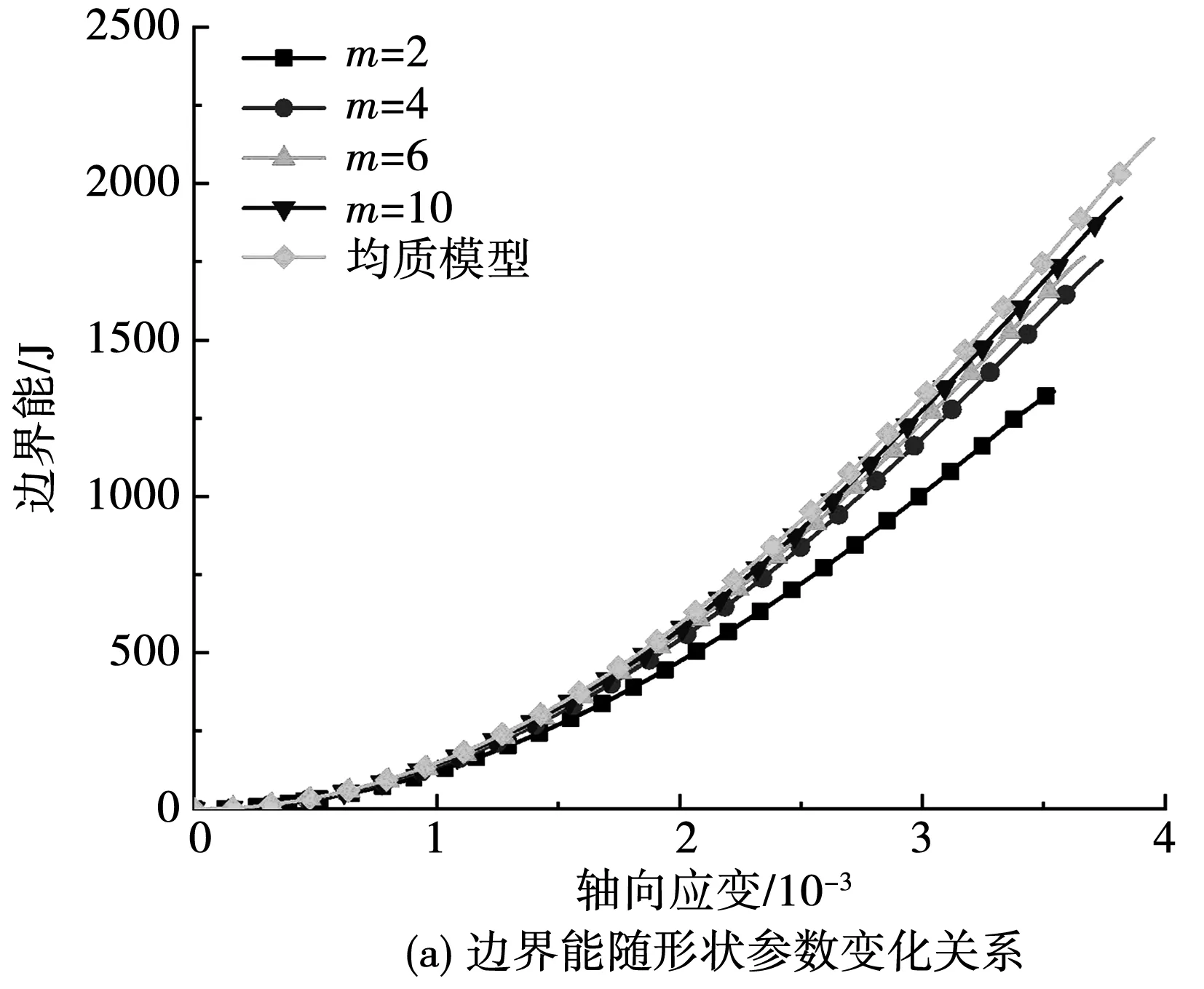
由图7可知，力学参数的非均质性对岩石能量演化具有很大影响。随着形状参数m由2增加至10，达到同一轴向应变时，边界能和总应变能逐渐增加，而颗粒动能、耗散能和摩擦能逐渐减小。当形状参数小时(如m=2)，模型非均质度高，在加载过程中，模型更加容易产生应力集中现象，使得微裂纹的萌生与扩展更加容易，从而使得微裂纹表面能所耗散的能量较少，耗散能较其他模型(如模型m=10)较少，且模型储存的总应变能也最小。因此，当模型中微裂纹扩展所需耗散能量小时，模型更加容易在加载过程中形成宏观可见的裂纹，使得模型的单轴压缩强度降低。

4 结 论

1) 力学参数的非均质性对岩石的宏观力学响应影响非常大。形状参数m越大，单轴压缩强度越高。弹性模量和单轴压缩强度随形状参数m拟合成指数函数关系，泊松比随形状参数m拟合成线性函数关系。

2) 声发射大致可分为4个阶段：初始压密阶段、弹性阶段、峰前塑性阶段和峰后破坏阶段。非均质度对声发射特征有一定的影响。当形状参数m小时，模型力学参数分布不均匀，初始压密阶段会随机产生一定量的声发射信号；而当形状参数大的时候，初始压密阶段则基本没有声发射信号。

3) 随着形状参数m增加，同一轴向应变时，边界能和总应变能逐渐增加，颗粒动能、耗散能和摩擦能逐渐减小。