分部积分法的解构和重构
——兼简论不定积分的定义和求不定积分的思想方法与一般思路
2021-06-08董春芳石德刚
董春芳,石德刚
(天津工业职业学院,天津 300400)
分部积分法是一元积分学中求积分时常用的重要方法。初学者在学习的过程中往往对如何选取u与v′以及在什么情形下需要运用分部积分法感到困惑,因此分部积分法是学生学习一元积分学时感到难以掌握的积分方法。本文对分部积分思想的理论依据进行解构和重构,总结出选取u与v′的原则和运用分部积分公式的模式。下面举例说明如何运用分部积分法求积分,以帮助初学者更好地学习和掌握分部积分法在积分运算中的运用。
一、分部积分公式
相应于两个函数乘积的微分法,可以推出另一种基本积分法——分部积分法,分部积分法主要用于求被积函数是两类不同函数的乘积且不具备凑微分法特征的积分。
设函数u(x)、v(x)具有连续导函数,由函数乘积导数、微分公式有(u·v)′=u′v+v′u、d(u·v)=vdu+udv,移项得u·v′=(u-v)′-v·u′、udv=d(u·v)-vdu(1).
对式(1)两端求不定积分,得不定积分的分部积分公式

对式(1)两端求从a到b的定积分,得定积分的分部积分公式
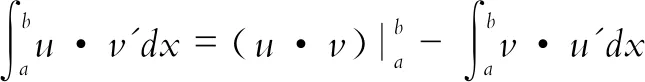
二、选取u与v′的原则与分部积分公式运用模式
用分部积分公式求一个函数的积分,需要将被积函数看作是两个函数u和v′的乘积,这就有个以什么函数为u,从而定出什么是v′的问题。因此正确地选择u与v′是运用分部积分法的关键所在。

(一)u经过求导,使u′变得简单,而v′和v的类型相同或复杂程度相当,例如,当被积函数为幂函数(代数函数)和三角函数或指数函数的乘积时,设幂函数(代数函数)为u(参见例1、例2)。
(二)u经过求导,使u′的类型与v的类型相同或相近(参见例5),例如,当被积函数为幂函数(代数函数)和对数函数或反三角函数的乘积时,设对数函数或反三角函数为u(参见例3、例4)。

(三)被积函数为不便于拆分为其它函数的单个函数[f(x)]n(n∈N+)时,一般设u=[f(x)]n
(n∈N+)(参见例6、例7);若[f(x)]k(1 解 设u=x,则v′=sinx,且u′=1,v=-cosx,从而 解 设u=x,则v′=e-x,且u′=1,v=e-x,从而 当分部积分公式运用比较熟练后,就不必写出u和v′,心里默记住u是什么和v′是什么即可直接使用分部积分公式。 该类型题的特点是,对公式左端的两个不定积分中的任何一个不定积分分部积分就可消去另一个不定积分,但是若对两个不定积分都分部积分,则可能两个不定积分都难以求出。 由该结论,要求I1(或I2),可以选择I2(或I1),若能较易求得I1-I2,则不仅可求得I1(或I2),而且同时求出了I2(或I1)。 本类型题的特点是,单独求I1(或I2)都需用两次分部积分公式并产生循环情形,即等式的右边出现KI1(或KI2),再移KI1(或KI2)至等号左边来求出I1(或I2)。 当被积函数含有以正整数n为指数的因子时,求该积分时一般都用分部积分法建立递推公式(使用递推公式计算积分层次清楚,便于检查,且不易出错)。 =-cscn-2xcotx-(n-2)In+(n-2)In-2 证 由不定积分的分部积分公式与等式x=f[f-1(x)]得 设函数u(x)、v(x)具有直至n+1的连续导函数,则有 …… 上面“得”字后各式由下往上依次代入,并保留第一式左端的积分和最后一式右端的积分,即得分部积分公式的推广形式. 分部积分公式的推广形式也可以写成表格形式: u各阶导数uu'u″u‴…(-1)n+1u(n+1)v(n+1)的各阶原函数v(n+1)v(n)v(n-1)v(n-2)v 解 设u=x2、v‴=cosx,则 x2各阶导数x22x20cosx的各阶原函数cosxsinx-cosx-sinx 当被积函数(两类不同函数的乘积)中有一个因子为对数函数或反三角函数时,不宜使用分部积分公式的推广形式。 当上面的表格中同一列的两个函数的乘积等于所给被积函数的常数倍时,求各阶导数与求vn+1的各阶原函数的工作就不需要再进行,利用解方程组的方法就可以迅速求得所给积分。 高等数学(微积分、数学分析)教材一般都是在微分学中建立泰勒公式,不仅过程较为繁杂,而且难度较大。但是用分部积分法建立泰勒公式的过程是较为简单的。 式(6)称为积分型余项. 证 只证x0 由牛顿—莱布尼茨公式和分部积分法(连续用)得 …… 式(7)称为柯西型余项. 式(8)称为拉格朗日型余项, 用函数f(x)的泰勒多项式近似代替函数f(x),需要估计误差(泰勒级数的余项Rn(x))。从泰勒公式的证明可以看出,导出Rn(x)的表达式的过程较为繁杂。但是从泰勒公式的证明也可以看出,证明泰勒公式事先并不需要知道泰勒级数的余项Rn(x)的表达式,这启示在不知道泰勒级数的余项Rn(x)的表达式的情形下,也可以给出|Rn(x)|的上界的估计。 证 只证x0 …… 原函数定义是非“构造性”的,原函数定义只表明,若函数F(x)是函数f(x)的一个原函数,则有F′(x)=f(x),因此,根据原函数定义并不知道从函数f(x)出发,经过怎样的运算能求得函数f(x)的原函数F(x),即原函数定义并未明确指出求原函数的途径,从而求不定积分(除少数标准类型外)并没有一个固定的格式可循,往往带有试探性质。 以上阐述表明积分法虽然是微分法的逆运算,但是求不定积分的思想方法与求导数的思想方法有本质的区别,且求一个初等函数的不定积分远比求一个初等函数的导数困难得多。下面简述求不定积分的思想方法。 1.将要求的不定积分设法转化成基本积分表里已有的积分(简称为表列积分,它的答案是已知的),是解答不定积分问题必须明确的一个基本原则。 2.熟悉和牢记将要求的不定积分转化成表列积分的三种积分法——直接积分法、换元积分法、分部积分法的使用方法与适用范围,一般来说,对被积函数作适当的恒等变形后,才能充分使用这些方法,而且每种方法的运用,往往视具体题目而定,有时解答一个题目仅用一种方法还不行,需要综合使用这些方法(参见例2、例6、例14、例15),因此,较多且准确的掌握各种积分类型的特点,以及与之相适应的积分方法(特别是针对被积函数特点而引入的各种换元积分法),成为解答不定积分问题的关键所在。 必须指出的是,只有多做练习,且在练习中随时注意被积函数的类型和特点,并体会转化被积函数的方法,才能增强观察的敏锐性和积淀成功的经验,从而提高简洁、准确、迅速地求解不定积分的能力。
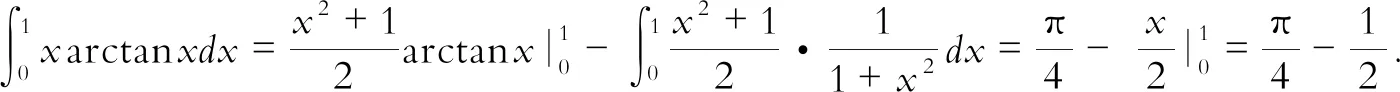
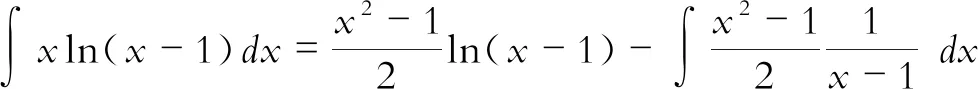
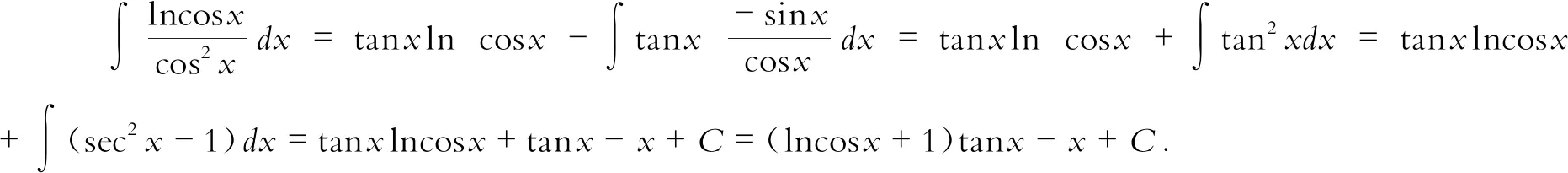


三、简论不定积分的定义与用公式及用方程组求不定积分
(一)简论不定积分的定义


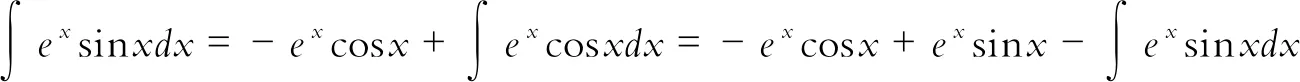


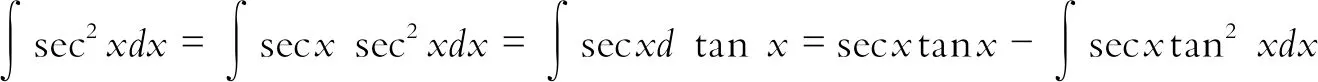

(二)用公式求不定积分
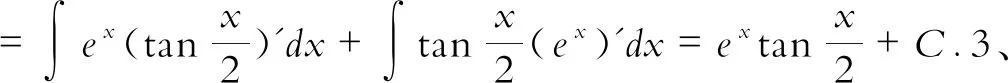





四、用分部积分法建立递推公式
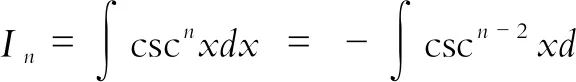

五、反函数的不定积分和不定积分的分部积分公式的推广形式
(一)反函数的不定积分
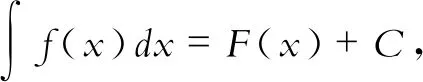
(二)不定积分的分部积分公式的推广形式
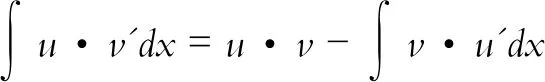


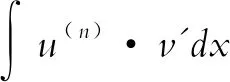




六、用分部积分法建立泰勒公式及泰勒级数的余项的绝对值的上界的估计
(一)用分部积分法建立泰勒公式
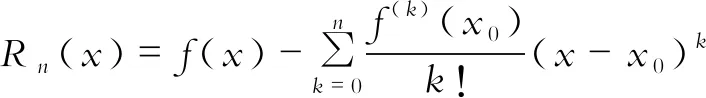



(二)泰勒级数的余项的绝对值的上界的估计

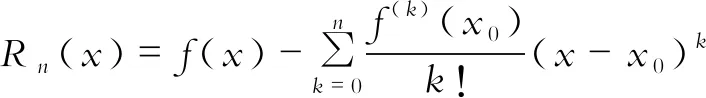
七、不定积分的思想方法和一般思路:
(一)求不定积分的思想方法
(二)求不定积分的一般思路


