分种群遗传算法的含分布式电源配电网故障定位

蔡伟强,洪 炎,徐 涛

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

目前，在新能源政策的推动下，分布式电源DG逐渐接入配电网，造成配电网结构发生变化，配电网稳定性随之变差，增大了配电网的故障定位难度，同时由于外在因素原因，故障定位的电流信息会发生畸变，使得配电网故障定位更为困难.为解决此问题需要一种新的能够提高配电网的安全性和稳定性的算法.

针对配电网故障使用的定位方法有:直接算法，即矩阵算法[1-2]，是一种简单快捷高效的方法，计算速度快，但对信息发生畸变的故障定位准确性较差，容易受到错误信息影响，定位不准确.

常见的算法有粒子群算法[3]、人工神经网络算法[4]、免疫算法[5]、蚁群算法[6]等.人工智能算法在配电网故障定位中虽然容错性能高，能够对信息发生畸变时提高定位准确率，但却在算法运行时需要处理大量的数据，效率低.

遗传算法[7-12]具有全局搜索能力强、容错性高、运算步骤简单等优点，但是运算时容易早熟，后期搜索能力较差，常对遗传算法进行改进来提高性能.

当配电网中接入多个分布式电源后，对配电网造成影响，使其结构和潮流方向改变，影响了传统的故障定位精度.近年来，对智能算法的故障定位因其定位准确，容错性高而受到重视，本文对遗传算法的初始种群进行改进，采用分种群方法，使每一个种群分别代表不同故障类型，通过仿真验证，得出该改进的遗传算法在已有的智能算法优点基础上具有对单重故障、双重故障等少重故障定位上，定位更加准确、运算效率高、计算速度快，具有一定的实用性.

1 算法定位原理

1.1 编码方法

配电网中的馈线终端单元FTU用来采集开关故障电流状态信息，将数据传输到配电网控制中心，进行信息处理.由于分布式电源的接入使得传统的算法编码方式不再适用，在含有分布式电源的配电网中需要对正方向进行规定，如图1所示，规定正方向为主电源到DG的方向，当K点发生故障时，S1、S2的故障电流方向跟正方向一致，其编码为1.S3、S4、S5的故障电流与正方向相反，其编码为-1.

图1 含DG配电网络图

用Ij表示第j个开关的状态.即

(1)

1.2 建立开关函数

当配电网运行时在某一时刻发生故障，FTU检测的开关电流越线信号发送给SCADA系统中，此时的信息不是故障线路信息，需要建立一个开关函数将开关电流越线信号转换成故障线路信息，使得每个分段开关与每个线路区段相关联.

对于含分布式电源的配电网，需要对开关函数进行改进，使其在含有多个分布式电源的情况下也能够适应，采用文献[7]中的开关函数，建立逻辑关系公式为

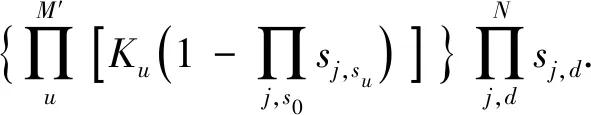
(2)

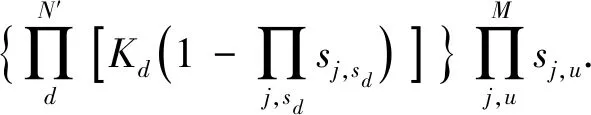
(3)

(4)

1.3 适应度函数的构造

适应度函数构造是否合理在遗传算法故障定位中起到重要作用，适应度函数的构造能够将算法与配电网故障定位相联系，适应度函数构造越合理，遗传算法故障定位越精确，根据故障电流信息经过开关函数运算后转变为故障电路信息，再算出种群中所有个体的适应度值，其适应度函数为

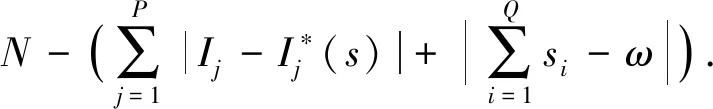
(5)

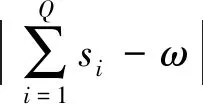
2 改进遗传算法的故障定位

2.1 初始种群的改进

遗传算法中初始种群的生成是随机生成的，其中包含所有故障种群，当配电网发生单重故障时，算法对初始种群进行筛选，会消耗大量的时间处理单重故障以外的种群个体.本文对遗传算法中初始种群的改进在于以故障类型来生成不同的种群，如单重故障对应的初始种群为[a1a2a3a4…ai](其中i为配电网联络结构图中区段的个数)单重故障时，生成的初始种群中a1a2a3a4…ai中有且只有一位ak(k∈[1,i])为1，其余全为0.双重故障对应的初始种群为[a1a2a3a4…ai](其中i为配电网联络结构图中区段的个数)，生成的初始种群中a1a2a3a4…ai中有且只有两位ak、aj(k∈[1,i]、j∈[1,i]其中k≠j)为1，其余全为0.最多只能生成i个种群，在算法运行时根据故障个数生成相应的种群.以i=10为例，对于一到三重故障生成初始种群，其中随机抽取的单个个体如表1所列.

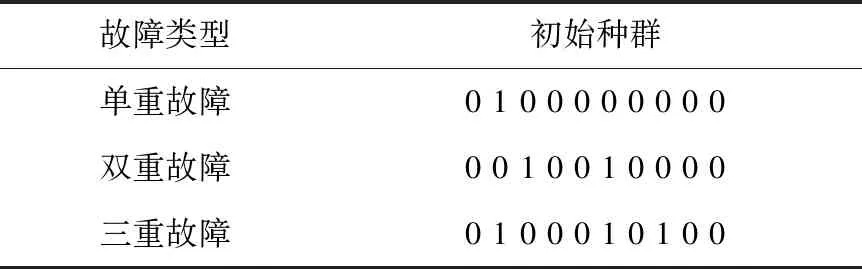
表1 生成初始种群的随机个体

2.2 单体交叉

对个体交叉进行改进，使用单体交叉在确保各种群所代表的各重故障不变的情况下，增加种群中个体的多样性.适应度函数对种群个体进行评估时，在选择最优解时能够在最小范围进行种群中个体基因的变动，从而更快地获得最优解.以图2配电网结构为例，生成三重故障种群时，其中某一个体基因为001010100000时，如果进行单体交叉操作，与另一个体基因001100100000进行交叉时，生成新的个体基因为001110100000，此个体不再是三重故障的个体.当使用单体交叉时，生成三重故障种群时，其中某一个体基因也为001010100000时，进行单体交叉时，随机选择其中某一位进行交叉，如第3位和第4位进行交叉，交叉后的个体基因为000110100000，仍为三重故障种群的个体，其种类不变.

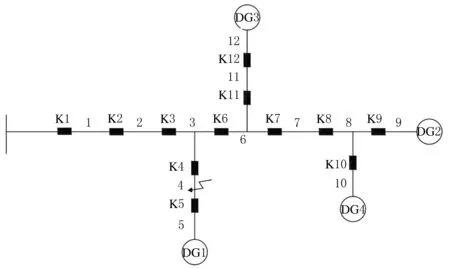
图2 配电网结构图

以图2线路4故障为例，设DG2=0，此时线路状态为

s1s2s3s4s5s6s7s8s9s10s11s12=000100000000.

(6)

此时开关函数的值为

Ij*(s)=1111-1-1-1-11-1-1-1.

(7)

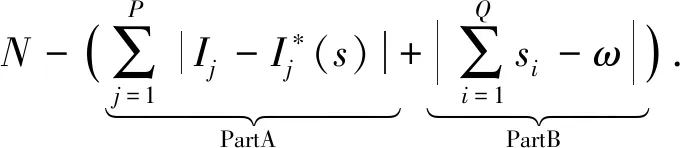
(8)

当准确故障定位时，FTU检测到线路故障，根据编码规则进行编码，反馈的值为

Ij=1111-1-1-1-11-1-1-1.

(9)

(10)

此时适应度函数取值最大

F1=N+ω-1.

当算法运算时，执行单重故障种群个体为001000000000，此时的开关函数值为

Ij*(s)=111-1-1-1-1-11-1-1-1.

(11)

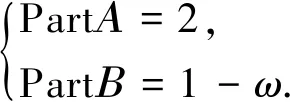
(12)

此时适应度函数值为

F2=N+ω-3.

(13)

如果靠传统的基因交叉变异，改变其中基因状态，可能会出现两个1的情况，如出现001010000000的情况，这时的PartΑ≥2，适应度值为F3，F3≤F2不利于得到最大适应度值，快速进行故障定位.执行单体交叉不但能够保持种群故障类型不变，还能够加速故障线路的寻优.执行单体交叉时

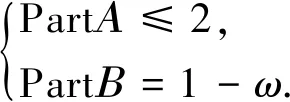
(14)

适应度函数取值

F4≥N+ω-3.

(15)

此时算法不会出现种群倒退的情况，同时保持相同的种群故障类型.

2.3 遗传操作

对遗传算法进行改进后，遗传操作也有相应的变化，添加了初始故障类型种群的生成，单体交叉，取消交叉变异操作，计算种群中每个个体适应度值，得到的适应度值最大时即得到最优解，把最优解解码，输出故障线路；否则对下一个故障种群进行评估，最终输出最优解.遗传算法故障定位流程如图3所示.

图3 遗传算法故障定位流程图

3 算例分析

3.1 单重故障

按照图2结构图搭建仿真模型，分布式电源DG1、DG3、DG4接入配电网中故为1，DG2没接入配电网故为0，利用FTU上传的信息输入目标函数，算法参数设置如下：DG1、DG3、DG4为1，DG2为0.设置每个种群数量为60，基因长度为12，最大迭代次数为50.

假设区段4发生短路，取N=100，w在本文中取0.5.根据上文的编码规则(1)和开关函数公式(2)、(3)、(4)计算相关的故障信息，结果如表2所列.

表2 各开关实际与期望状态值

根据已知的开关状态值，借助MATLAB，写入相应的评价函数，仿真结果如图4所示.

图4 故障点判断最优解

从图4可知，此改进算法对于单重故障能够快速进行故障定位，得到最优个体为4，即区段4线路发生故障，仿真结果与假设的故障线路一致，证明在含DG的配电网故障定位应用中此算法具有可行性.

3.2 多重故障

假设在图2所示配电网结构图中，区段4、区段8、区段12发生故障，根据已知的开关状态值，借助MATLAB，写入相应的评价函数，仿真结果如图5所示.

如图5得出，算法迭代9次后得到最优解，最优个体为4、8、12分别对应配电网结构图中的区段4、区段8、区段12.由仿真的结果可知与假设的故障线路位置一致，表明此算法在配电网故障定位中线路发生多重故障时能够进行准确定位.

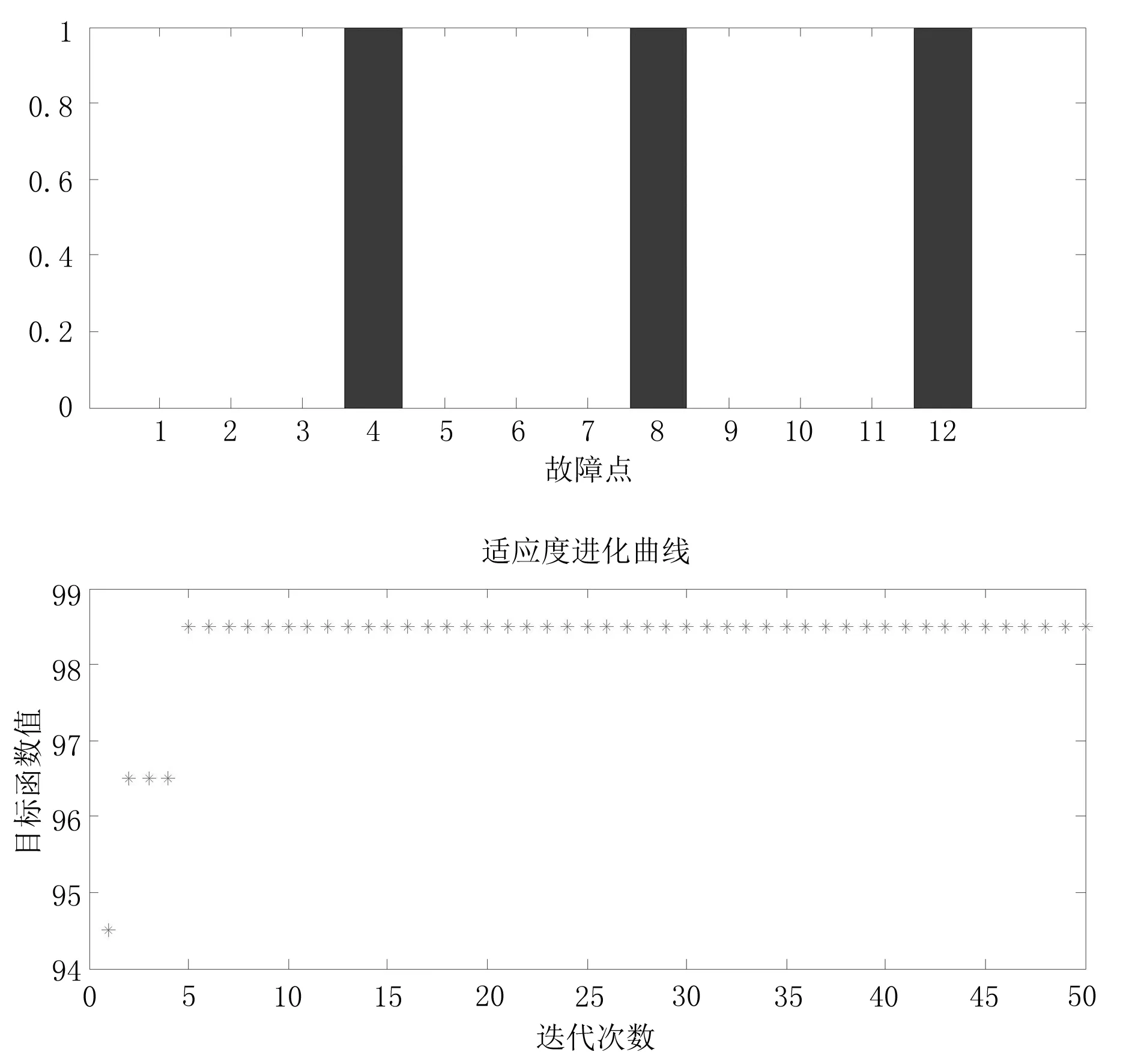
图5 故障点判断最优解

3.3 信息发生畸变

由于FTU会因为外界环境影响故障或是上传电流信息畸变，导致算法定位不准确，采用改进后的遗传算法进行故障定位时能够弥补之前算法的不足，以三重故障为例，假设区段4、区段8、区段12发生故障，受外界环境影响FTU信息发生畸变，使I7的值由“1”变为“-1”，写入发生畸变的开关状态值，仿真结果如图6所示.

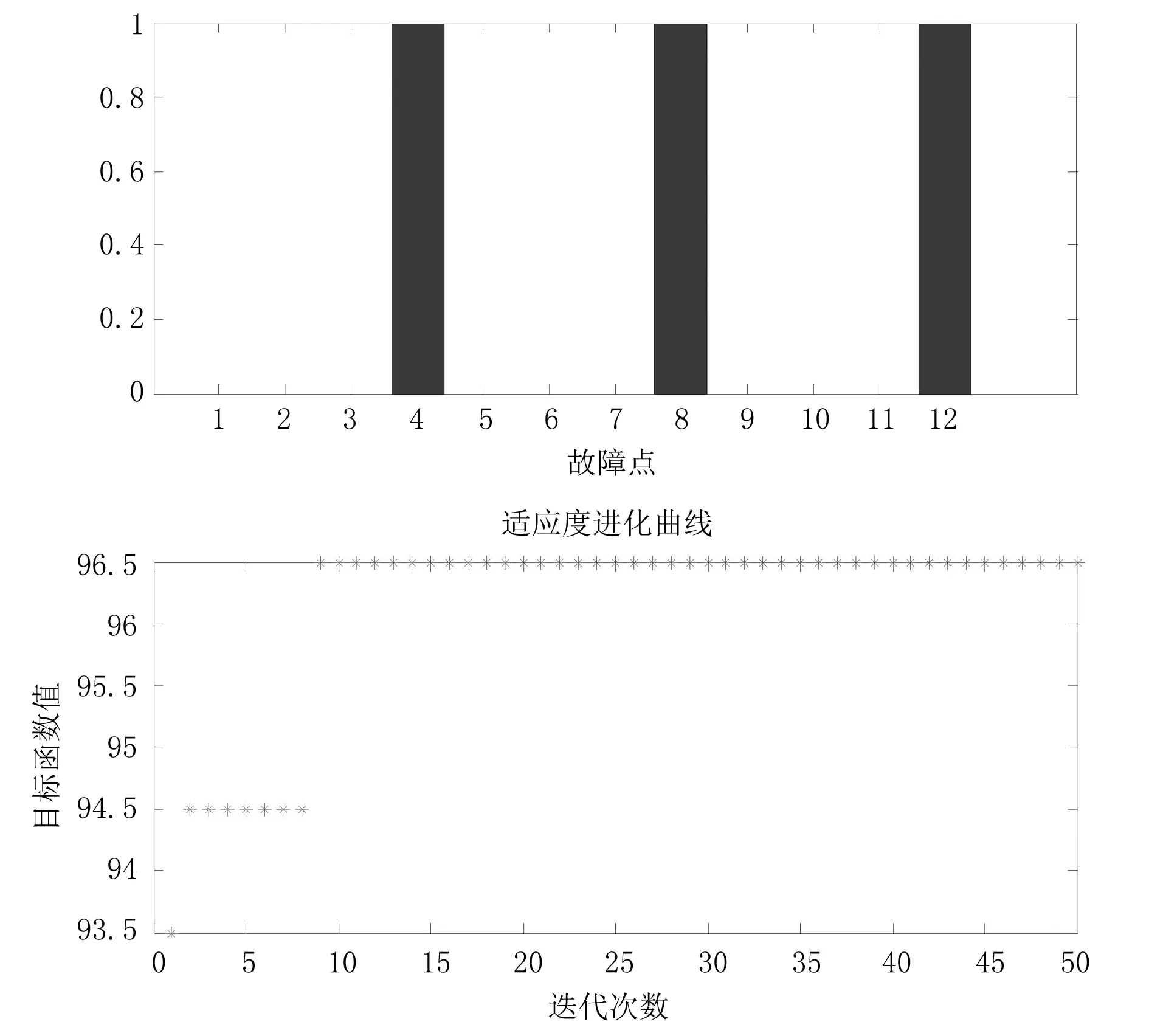
图6 发生畸变时故障点判断最优解

由图6可知，算法迭代11次后得到最优解，最优个体为4、8、12，与假设的区段4、区段8、区段12相对应.由此可知当FTU上传信息发生畸变时在含DG的配电网故障定位应用中该算法仍能够准确定位.

3.4 算法性能分析

上文对算法进行分析得出，此算法对配电网故障定位具有可行性，运算效率较快，准确率高.通过算例仿真验证当接收信息有畸变时也具有以上特性.表3为不同类型故障的仿真结果，当对算法的单重故障、两重故障、三重故障以及分别有畸变的情况下进行20次仿真，对各类型的故障平均迭代次数、正确次数进行分析.

表3 不同类型故障仿真结果

由表3可知，对单重故障、两重故障、三重故障进行定位时，单重故障的迭代次数很少，算法效率很高，准确率也较高；两重故障、三重故障的迭代次数也不多，准确率很高.该算法能准确地在上传信息有畸变的情况下进行故障定位，证明了该算法在配电网故障定位应用中具有一定的应用价值.

4 结语

本文提出了一种对初始种群进行改进的遗传算法能够对含有多个DG的配电网故障快速定位，对遗传操作中的交叉步骤进行改进，加入单体交叉，能够加快算法的快速性，同时也维持了故障种群类型.此算法在进行单重故障、两重故障等低重故障时能够快速、准确进行定位，仿真结果表明，改进的遗传算法对带分布式电源的配电网故障定位具有良好的容错性，算法的效率和准确性也都很高.