再生混凝土受压细观损伤尺寸效应分析
2021-06-08黄一凡王向东
黄一凡, 王向东
(河海大学 力学与材料学院, 江苏 南京 211100)
再生骨料是将废弃混凝土进行破碎、清洗,并按一定比例和级配混合而成的骨料,再生混凝土是用再生骨料代替天然骨料配制成的新的混凝土[1].再生混凝土在细观层次上是一种五相复合材料,拥有比普通混凝土更为复杂的细观结构和力学性质,但目前对再生混凝土的细观层次的研究较少.由于试验易受环境因素和骨料来源的影响,各国学者得出的结论大相径庭[2].为了从细观层次研究混凝土的力学性能,许多学者建立了细观力学模型.Schlangen[3]应用格构模型模拟混凝土损伤断裂的过程,但由于采用简单的线弹性本构关系和破坏准则,模拟的混凝土受压过程差异较大.Mohamed等[4]在混凝土的宏观破坏行为与细观裂缝发展有直接关系的前提下,提出混凝土内部结构细观模型(M-H模型).该模型考虑骨料和力学性质的随机分布,但假定骨料和砂浆之间只传递压应力,忽略剪切应力.刘光廷等[5]在随机粒子模型的基础上提出随机骨料模型,并模拟混凝土的三相细观骨料模型,提出断裂韧性和强度破坏综合准则,采用非线性有限元法模拟单裂纹拉伸试件从损伤到断裂破坏的全过程,为混凝土破坏机理的研究及混凝土强度的计算提供新的技术途径.
本文采用随机骨料模型模拟再生混凝土五相细观力学模型,选择混凝土损伤塑性(CDP)模型作为再生混凝土细观损伤的本构并分别赋予五相不同的材料参数,从抗压强度、应力-应变曲线和损伤的角度研究再生骨料替换率为80%时尺寸效应的影响.
1 再生混凝土随机骨料模型
再生混凝土的骨料形状最接近多边形,再生骨料的表面均匀附着旧界面,从内到外分别是旧水泥砂浆、新界面和新水泥砂浆.再生混凝土细观模型,如图1所示.

图1 再生混凝土细观模型Fig.1 Meso model of recycled concrete
为了模拟再生混凝土真实的密度和强度,选择的骨料粒径和数量是由富勒曲线中导出的累积分布函数[6]决定.基于Walraven公式,任一点不同骨料粒径的概率Pc为
(1)
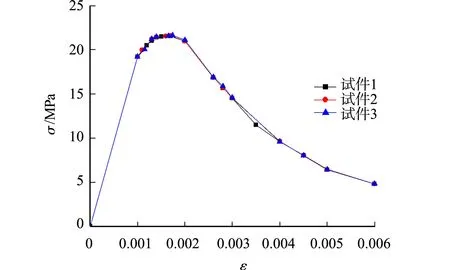
式(1)中:D 再生骨料的替换率为80%,骨料的占比率为60%.根据不同的试件尺寸,可求得各粒径骨料的数量,再通过蒙特卡洛法确定骨料圆心的位置.从大到小依次投放骨料,同时,判断骨料之间是否会碰撞,并预留界面的位置,即旧界面、旧水泥砂浆、新界面的厚度分别为0.5,1.0,0.5 mm.基于微观成像技术的研究[7],骨料与砂浆之间界面的厚度约为50~60 μm,但是数值计算中太小的尺寸无法承载和传递荷载,也难以收敛.因此,界面区厚度一般设为0.5~2.0 mm[8],文中界面的厚度为0.5 mm. 混凝土损伤塑性模型中塑性参数[9]的膨胀角为38°,偏心率(流动势偏移量)为0.1,双轴抗压强度和单轴抗压极限强度之比为1.16,K系数(屈服面形态)为0.666 67;粘性系数(数值越大越接近液体)一般取0.000 1. 单轴受拉时,再生混凝土各相应力(σ)-应变(ε)曲线参数为 σ=(1-dt)Ecε, (2) (3) (5) 式(2)~(4)中:dt为单轴受拉损伤演化参数;αt为单轴受拉应力-应变曲线下降段的参数[10];ft,r为单轴抗拉强度;εt,r为与单轴抗拉强度代表ft,r相对应的峰值受拉应变. 单轴受拉应力-应变曲线的参数取值,如表1所示. 表1 单轴受拉应力-应变曲线的参数取值Tab.1 Parameter selection of uniaxial tensile stress-strain curve 单轴应力-应变曲线,如图2所示.图2中:fc,r为单轴抗压强度;εc,r为与fc,r相应的峰值受压应变;εcu为应力-应变曲线下降段0.5fc,r时的受压应变;负值为受拉,正值为受压. 图2 单轴应力-应变曲线Fig.2 Uniaxial stress-strain curve 单轴受压时的再生混凝土各相应力-应变曲线参数为 σ=(1-dc)Ecε, (5) (6) (7) (8) 式(5)~(8)中:αc为单轴受压应力-应变曲线下降段参数值dc为单轴受压损伤演化参数[10]. 单轴受压应力-应变曲线的参数取值,如表2所示. 表2 单轴受压应力-应变曲线的参数取值Tab.2 Parameter selection of uniaxial compression stress-strain curve 图3 加载方式与边界条件Fig.3 Loadingmode and boundary conditions 为研究尺寸效应的影响,建立3种尺寸,每种尺寸有3组试件,共9组再生混凝土试件.根据代表性体积元法(RVE)[11],试件的边长应大于等于3倍的最大骨料粒径.因此,75 mm×75 mm与100 mm×100 mm的试件为一级配,150 mm×150 mm的试件为二级配.对模型采用位移加载的方式,在试件上部,每个步长向下压0.005 mm的位移荷载,其加载方式与边界条件示意图,如图3所示. 再生混凝土材料参数[12],如表3所示.表3中:E为弹性模量;fc为抗压强度;ft为抗拉强度;ν为泊松比.由表3可以计算再生混凝土各相材料的拉伸损伤参数与压缩损伤参数,以及随机多边形骨料在单轴受压条件下各相材料的拉伸损伤参数与压缩损伤参数. 不同尺寸的再生混凝土五相细观模型,如图4所示.图4中:试件1,2,3尺寸为75 mm×75 mm;试件4,5,6尺寸为100 mm×100 mm;试件7,8,9尺寸为150 mm×150 mm. 表3 再生混凝土材料参数Tab.3 Material parameters of recycled concrete (a) 试件1 (b) 试件2 (c) 试件3 (d) 试件4 (e) 试件5 (f) 试件6 (g) 试件7 (h) 试件8 (i) 试件9图4 不同尺寸的再生混凝土五相细观模型Fig.4 Five phase meso model of recycled concrete with different sizes 与传统圆形骨料相比,多边形骨料存在尖锐角,很难通过骨料与砂浆之间的网格过渡区域,因此数值计算过程极易不收敛.故采用四边形为主的整体划分进阶算法,允许多边形骨料在过渡区域使用三角形网格,这样能很好地吻合网格与种子的位置,特别是尺寸较小的界面层.网格划分示意图,如图5所示.全局种子尺寸为0.5 mm,最大偏离因子为0.1. 图5 网格划分示意图Fig.5 Schematic diagram of grid division 试件应力-应变曲线,如图6所示. (a) 75 mm×75 mm (b) 100 mm×100 mm (c) 150 mm×150 mm图6 试件的应力-应变曲线Fig.6 Stress-strain curve of specimens 尺寸为75 mm×75 mm的再生混凝土试件中,最大骨料粒径为17.5 mm,最小骨料粒径为7.5 mm,骨料的占比率为60%.由图6(a)可知:这一组试件的抗压强度分别为21.54,21.57,21.63 MPa,峰值应变约为0.001 70.因此,取其平均值21.58 MPa作为该组试件的抗压强度. 尺寸为100 mm×100 mm的再生混凝土试件中,最大的骨料粒径为17.5 mm,最小的骨料粒径为7.5 mm,骨料的占比率为60%.由图6(b)可知:这一组试件的抗压强度分别为20.58,20.48,20.74 MPa,峰值应变约为0.001 67.因此,取其平均值20.60 MPa作为该组试件的抗压强度. 尺寸为150 mm×150 mm的再生混凝土试件中,最大骨料粒径为32.5 mm,最小骨料粒径为10 mm,骨料的占比率为60%.由图6(c)可知:这一组试件的抗压强度分别为19.43,19.20,19.26 MPa,峰值应变约为0.001 64.因此,取其平均值19.30 MPa作为该组试件的抗压强度. 由图6可知:随着试件尺寸的增大,抗压强度随之减小,与75 mm×75 mm的试件相比,100 mm×100 mm和150 mm×150 mm试件的抗压强度分别下降4.5%和8.3%,对峰值应变的影响很小.计算结果与试验值19~28 MPa较为符合[13],差异主要是因为骨料粒径和参数存在差异. 9个试件的最终损伤图和应力云图,如图7所示.图7中:试件1,2,3的最终损伤平均值0.92;试件4,5,6的最终损伤平均值0.89;试件7,8,9的最终损伤平均值0.85.由对再生混凝土圆形骨料损伤的研究[14]可知:初始损伤出现在旧界面,随后损伤依次出现在外界面、老水泥砂浆和新水泥砂浆. 由图7可知:多边形骨料的损伤与传统圆骨料的扩展有略微不同,初始损伤出现在内界面,随后出现在外界面,两者的损伤带发展贯通旧水泥砂浆,随后向新水泥砂浆发展,并最终贯通整个试件;每个尺寸的试件损伤发展方向都呈45°或135°,损伤出现的区域基本和应力云图中应力集中的区域吻合,应力集中于骨料的内、外界面;随着试件尺寸的增大,损伤会更加均匀地出现在试件的各处,损伤极限更低. (a) 试件1 (b) 试件2 (c) 试件3 (d) 试件4 (e) 试件5 (f) 试件6 (g) 试件7 (h) 试件8 (i) 试件9图7 再生混凝土不同尺寸损伤图和应力云图Fig.7 Damage diagram and stress nephogram of recycled concrete with different sizes 建立再生混凝土五相任意多边形随机骨料模型,应用损伤塑性模型,研究了试件尺寸对再生混凝土单轴受压抗压强度和损伤断裂的影响,得到以下3个结论. 1) 试件尺寸对再生混凝土的宏观力学性能影响显著,随着试件尺寸的增大,再生混凝土试件的抗压强度和峰值应变随之降低.这是因为试件尺寸越小,单位体积下的孔隙、裂缝和薄弱处就越少. 2) 多边形骨料的损伤发展与圆形骨料略有不同,内界面出现初始损伤后,外界面出现损伤,内外界面的损伤发展贯通旧水泥砂浆,随后沿着45°或135°向新水泥砂浆中发展,而圆形骨料是内界面出现损伤后向外依次出现损伤.这一现象的原因是,圆形骨料的应力-应变状态是各向同性的,而多边形骨料的应力-应变状态是各向异性的.在同等体积率下,多边形骨料的受力面积更大,更易发生应力集中,所以损伤会优先出现在薄弱处,即内外界面. 3) 试件尺寸对应力影响不大,每组试件的损伤处基本和应力云图中应力集中处吻合.随着试件尺寸的增大,最终损伤值也随之降低,且在较小尺寸的构件中损伤多集中发生在骨料较密处,呈现少而密;在较大尺寸的试件中,损伤会均匀出现在试件的各处,呈现多而疏.这是由于试件尺寸愈小,强度的离散性愈大,即尺寸较小时,骨料会相对集中,造成试件各处强度不均匀,从而使损伤少而密.2 混凝土损伤塑性模型
2.1 塑性参数
2.2 拉伸损伤参数


2.3 压缩损伤参数


3 数值模拟
3.1 模型的建立
3.2 材料参数




3.3 网格划分

3.4 试件尺寸对应力-应变曲线的影响

3.5 试件尺寸对应力和损伤的影响



4 结论
