用Matlab软件仿真磁聚焦实验
2021-06-07张林
张 林
(南京林业大学 理学院,江苏 南京 210037)
磁聚焦是电子在非垂直磁场中运动的一个重要应用,并被广泛应用于阴极射线管(CRT)显示器中。学生通过学习磁聚焦现象,不仅可以认识到电子在非垂直磁场中做螺旋线运动,也能明白显示器中的热电子经过栅极后,运动一个螺距的位移,会重新汇聚到焦平面上。目前,研究人员在磁聚焦领域做了大量的工作,例如磁聚焦中电子纵向运动的计算机模拟[1],则使用磁聚焦技术测定电子的荷质比[2-4],这对于学生认识磁聚焦的本质具有重要的意义。在实验中,观察微观电子做螺旋线运动是非常困难的,对电子空间运动的测定更是不可能的。因此,希望使用Matlab软件建立电子在磁聚焦实验中的模型,通过改变电子的不同发射角,模拟其在空间的运动规律,并得出实验结论。
1 电子在磁聚焦实验中的运动模型
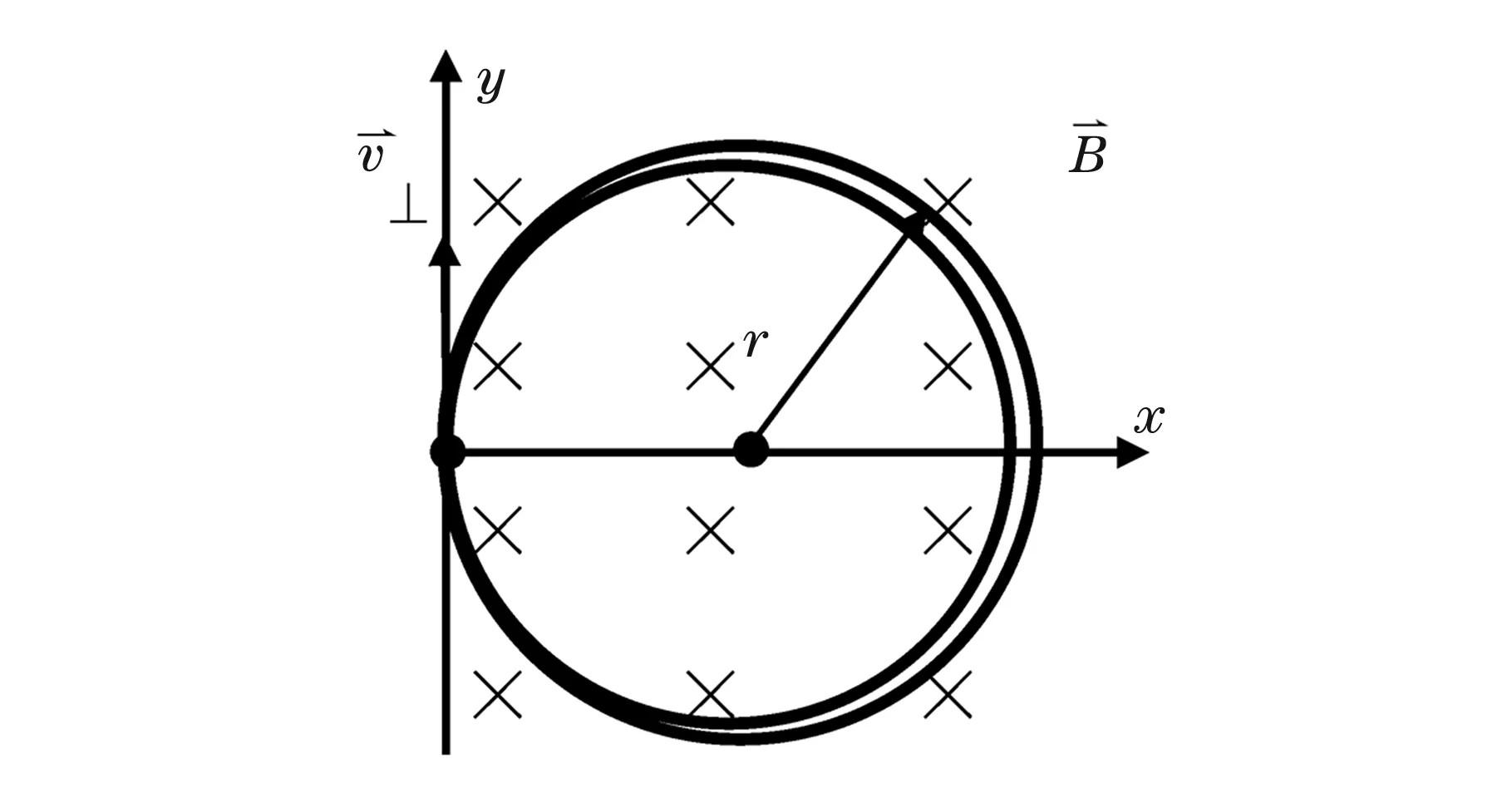
图1 磁聚焦中电子在x-y平面和空间的运动轨迹
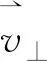
(1)
(2)
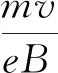
(3)
根据(3)式,就可以使用Matlab绘制出不同电子在空间的运动轨迹,如图1右图所示。
2 磁聚焦中电子空间运动的Simulink模型
本章将使用Matlab/Simulink仿真软件,对带电粒子在磁聚焦实验中的运动方程(3)式建立仿真模型。打开Matlab/Simulink仿真界面,如图2所示,建立一个共用的时钟Clock模块,用于电子在空间三个方向运动的计时。首先,来表示电子在x方向的运动,将Clock接入一个余弦函数模块(Cosine Wave function),并将其平方,用以表示(3)式中x方向的分运动因子cos2(t/2),再将其乘上一个正弦函数sinθ,再通过一个增益模块X1,就可以表示电子在x方向的运动。同样,由于电子在y方向的运动方程与其在x方向非常相似,因此只需要构建一个新的三角函数,用以表示(3)式第二个方程中的因子sin(t/2),利用已有的模块sin(t/2)和sinθ,只要将三者相乘,再通过一个增益Y1,就可以得到电子在y方向的运动,即(3)式的第二个方程。最后,再将时钟t乘以一个三角函数,就可以实现电子在z方向的运动。
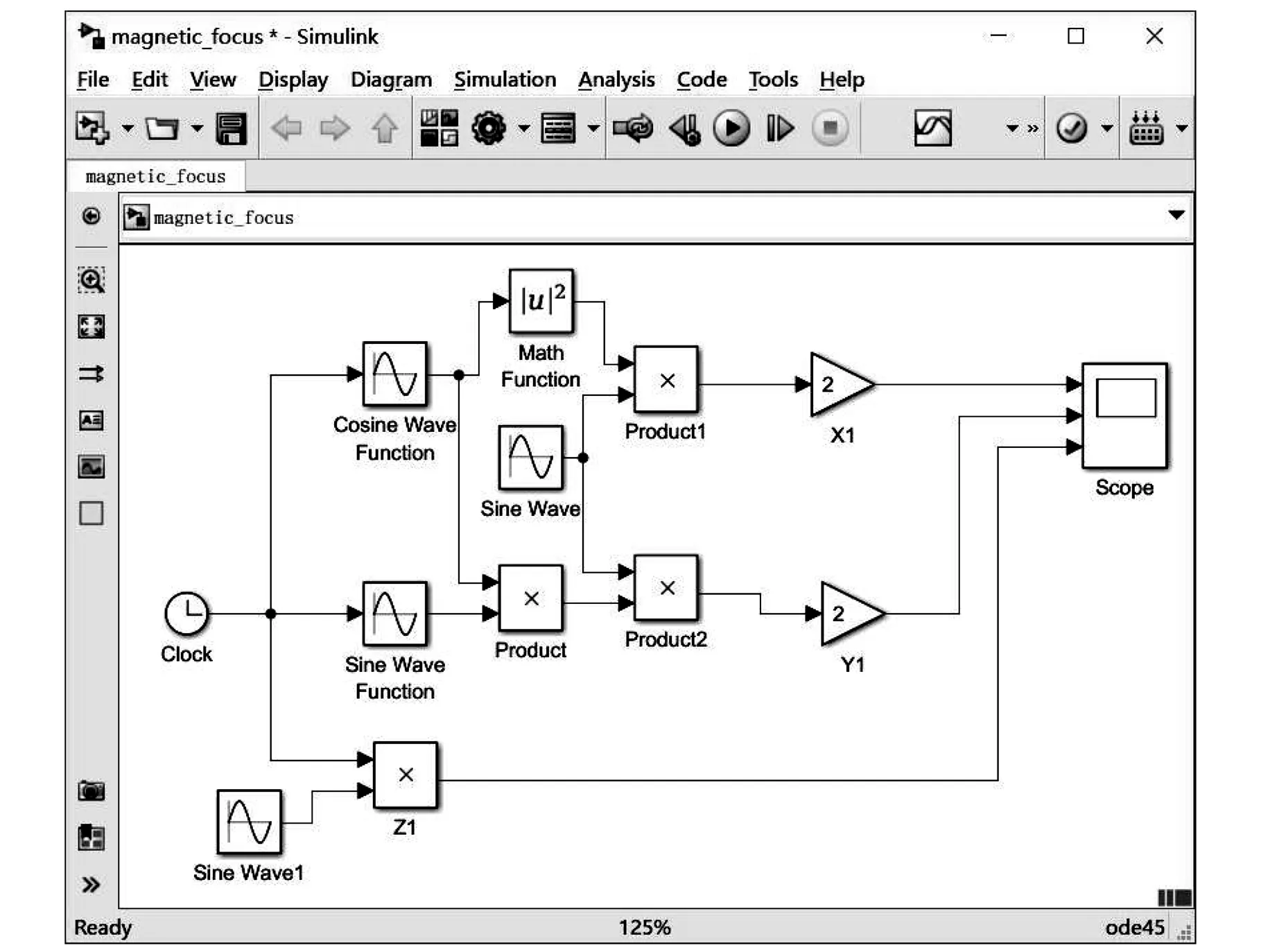
图2 电子在磁聚焦实验做空间运动的Simulink模型
最后将电子在x、y和z方向的分运动输入到一个三通道的虚拟示波器Scope中,运行仿真程序,就可以通过Scope观察到电子在各个方向上的运动图像。
3 仿真图像与结论
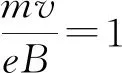

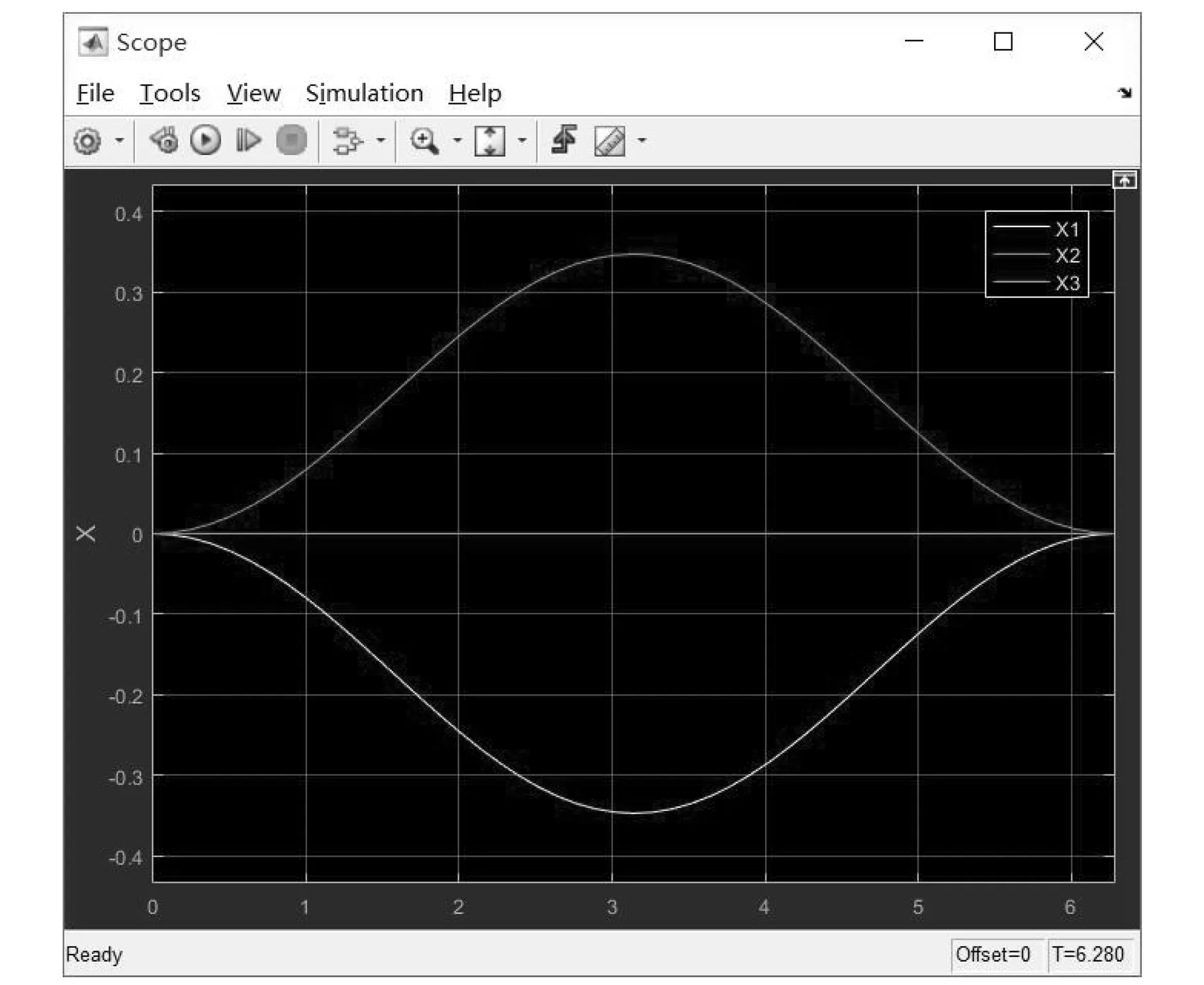
图3 发射角θ=-π/18,0,π/18时,电子在x方向的运动曲线
图4是当θ=-π/18(黄线),0(蓝线)和π/18(橙线)时,电子在y方向的运动曲线。电子在y方向的运动与x方向非常相似,其周期仍然为T=2π=6.28 s,与x方向的运动不同的是,电子y方向的运动轨迹是标准的正弦函数y∝2sin(t/2)cos(t/2)=sin(t),这是与方程(3)式中相符合的。同样,当反射角相反时,两电子的运动方向相反,当t=nπ时(其中n为整数),电子的y=0;当t=nπ+π/2时,y方向的位移达到最大,约为回旋半径r=0.175,是x方向最大位移的一半。同样,当发射角θ=0时,电子在x-y不做圆周运动,因此电子在y方向的位移始终为0。
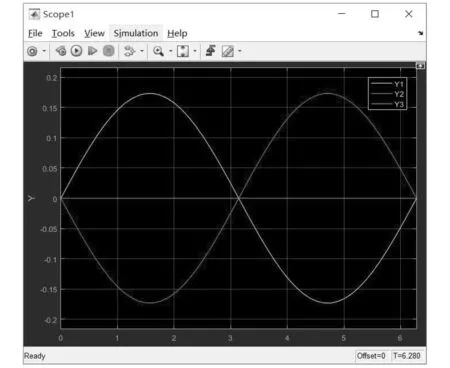
图4 发射角θ=-π/18,0,π/18时,电子在y方向的运动曲线

综合图3至图5的现象,可以得到以下结论:经过一个回旋周期T后,各电子具有相同的x,y和z的位置,因此各电子经过一个螺距后,会重新汇聚到磁透镜的焦点。

图5 发射角θ=-π/18,0,π/18时,电子在z方向的运动曲线
