页岩油藏微尺度流动特征及应力敏感性分析

赵国翔 ，姚约东 ，王链 ，陈依伟 ，张涛 ，于雯汀

（1.中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249；2.中国石油新疆油田分公司，新疆 克拉玛依 834000；3.陕西延长油田股份有限公司工程管理部，陕西 延安 716000；4.中海油田服务股份有限公司油田生产事业部，天津 300450）

0 引言

随着常规油气资源量的不断减少，以页岩油、致密油为代表的非常规油气资源逐渐成为勘探开发的新方向［1-5］。对页岩油在纳米孔中的传输机理进行定量表征，是研究页岩油滞留、运移及赋存状态的基础工作之一。但是，通过数值模拟、实验方法得到的经验公式不能完全揭示流体微尺度流动特征［1］。因此，有必要建立合理的数学模型，对微尺度流体的渗流机理进行描述。

微尺度条件下，由于流体-壁面作用力较强，常规尺度流体传输的数学模型不再适用，经典的达西定律及 Hagen-Poiseuille方程无法描述其传输机理［4-9］。Mattia等［10］基于实验及分子模拟结果提出了滑移长度模型，但无法考虑分子结构变化导致的滑移变化。Sun等［11］基于Mattia模型引入了修正因子，但未给出修正因子的计算方法，仍然需要经过实验或模拟才能确定其具体数值。Thomas 等［12］以及 Myers［13］根据实验及模拟结果分别提出了边界滑移模型，但无法反映流体-壁面作用力的影响。Wu等［6］基于Tolstoi模型，使用了表观黏度简化边界层的作用，导致微尺度效应的影响被高估。同时，低渗透油藏在开发过程中发生了应力敏感及介质变形现象，使得页岩油储层孔隙度、渗透率均发生变化，进一步增大了微尺度效应的影响［14-16］。因此，本文通过建立页岩纳米孔传输模型，描述了烷烃分子微尺度流动机理，并应用实验及分子模拟结果进行验证。

1 微尺度条件下的管流模型

模型的假设条件：1）毛细管中为单相牛顿流体流动；2）流体在毛细管中的流动为稳态层流；3）微尺度流动过程中满足连续介质假设；4）毛细管中流体分为体相部分及均质的边界层部分；5）整个流动过程为等温过程，不考虑温度变化。

1.1 单毛细管流动模型

微尺度条件下，流体-壁面作用力导致边界层流体物性与体相流体物性不同，且边界层流体流动速度不再为0。边界层流体及体相流体分别具有不同的流体黏度，且在不同的壁面条件下，其边界滑移速度及流速剖面也有所变化，如图1所示。图中：rb为体相流体半径，r0为毛细管半径，hi为边界层流体厚度，ls1为流体在无机孔中的滑移长度，ls2为流体在有机孔中的滑移长度，δ为烷烃分子层间的平均距离，ηi，ηb分别表示边界层流体及体相流体的分子流动性。

图1 烷烃分子在纳米孔中的流动机理示意

无限长等截面毛细管中，不可压缩流体体相部分的流动方程［7］为

其中

原油分子模拟结果［7］表明，边界层流体厚度约为2个分子层的厚度，本文取0.96 nm。

与体相流体类似，边界层流体的流动方程［8］为

式中：μi为边界层流体黏度，mPa·s；vi为边界层流体流速，m/s。

边界层部分与体相部分流动方程的边界条件为

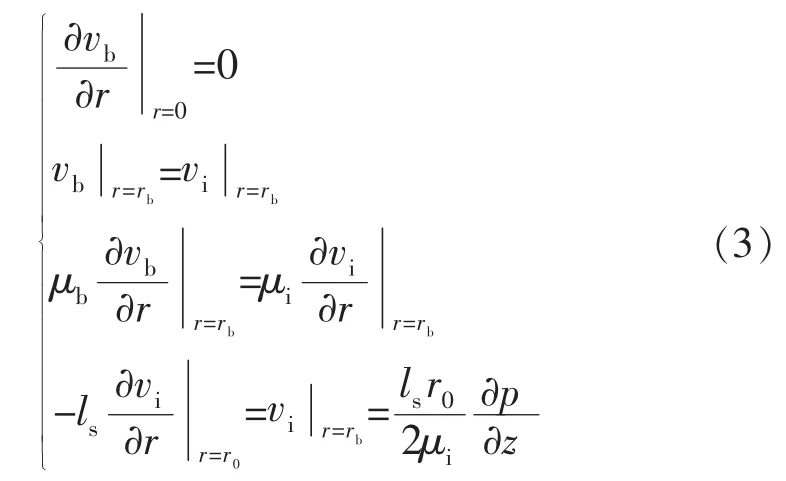
式中：ls为烷烃分子滑移长度，nm。

根据式（1）—（3），体相及边界层流体流速分别

式中：Δp为毛细管所受应力压差，MPa；l为毛细管长度，m。

对式（4）和式（5）分别进行积分，可以得到体相流体与边界层流体的体积流量qb，qi：

因此，毛细管内的总体积流量qt为

1.2 滑移长度模型

滑移长度与边界层流体及体相流体的分子流动性差异有关。边界层与体相的流体分子流动性之比［17］为

分子层间的平均距离δ约为0.5 nm。

分子流动性之比可由式（10）确定［18-20］：

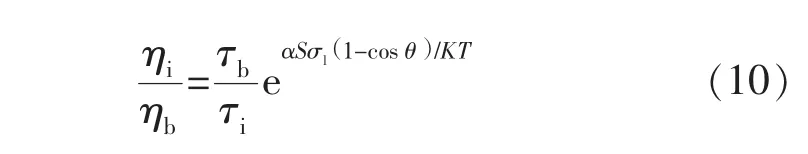
其中：

式中：τi，τb分别为边界层及体相流体的弛豫时间（由实验或分子模拟结果得到），s；K为玻尔兹曼常数；T为温度，K；αS为相邻层可流动分子的等效壁面面积，nm2；n 为烷烃分子中的碳链数量；θ为接触角，（°）；σl，σs分别为流体和固体壁面的表面张力，mN/m；φ为流体表面张力及固体壁面表面张力的极性贡献值和扩散贡献值之比（取值 0.85［6］）。

当考虑壁面粗糙度时，表观接触角会随着粗糙度的变化而变化，并且符合分形定律［21］，可表示为

式中：θapp为考虑壁面粗糙度时的表观接触角，（°）；lu，ll分别为圆锥形粗糙单元的高度和长度；D为粗糙度分形维数。结合式（9）—（13），得到 ls的计算公式：

实验及模拟结果表明，边界层流体与体相流体黏度之比与其平均弛豫时间比有关［22］，即：

1.3 应力敏感特征

当毛细管受压时，其应力发生变化，产生变形。由材料力学及胡克定律［23］可知，毛细管受压后，径向方向半径减小，形状不变，轴向方向则变长，可表示为

应力变化时，毛细管中体相流体半径rb′为

式中：r0′，l′分别为毛细管受压后的半径及长度，nm；E为弹性模量，GPa；F为所受应力，MPa；ν为泊松比。

1.4 考虑微尺度效应的流体传输模型

结合式（8）、（14）、（16）—（18），得到考虑界面滑移、边界层吸附、壁面粗糙度及应力敏感的液体传输模型：

为说明流体传输模型中微尺度效应及应力敏感导致的流量变化，引入增长因子ε，其为本文模型计算得到的体积流量与Hagen-Poiseuille方程的体积流量qHP之比，可表示为

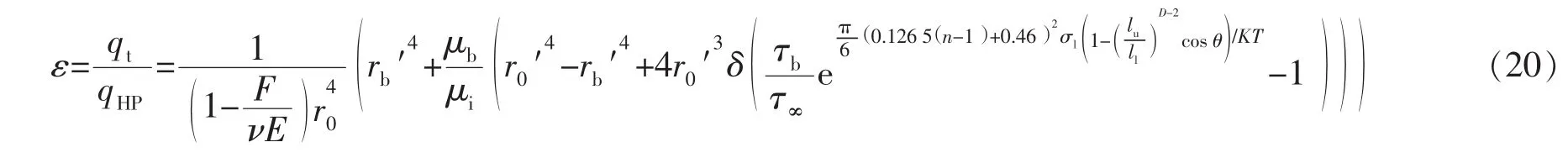
其中

2 模型验证

为验证模型的准确性，应用不同碳链长度烷烃微尺度实验及分子模拟结果进行验证。文献来源及其基本参数见表1。应用式（20）计算出不同烷烃分子的增长因子，并与文献数据结果进行了对比验证（见图2）。从图2可以看出，理论模型计算结果与文献数据基本吻合，说明新流体流动模型应用效果较好。

表1 文献来源及其基本参数

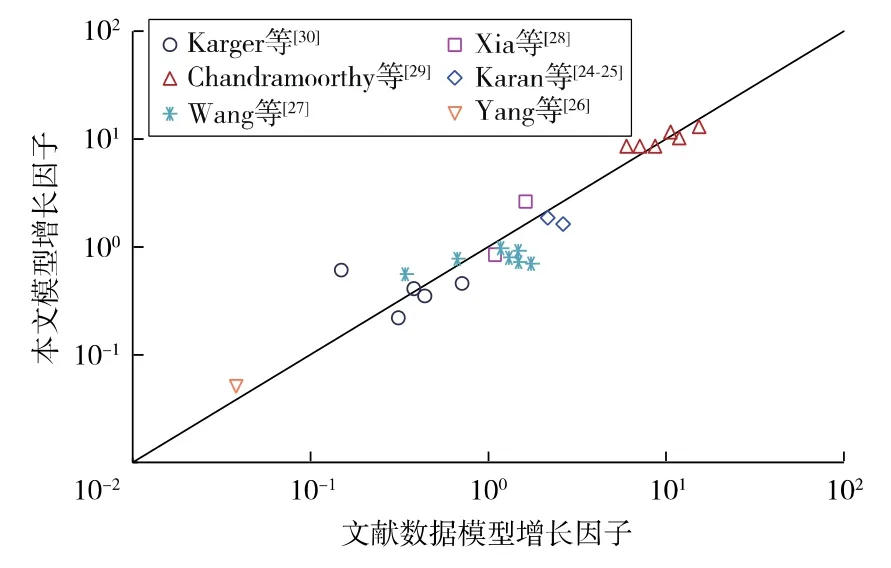
图2 本文模型计算的增长因子与文献数据对比

3 结果与讨论

由式（14）可知，滑移长度的确定与边界层流体和体相流体的弛豫时间比有关。Wu等［6］给出了20℃条件下不同烷烃分子的弛豫时间比（见图3），其边界层流体黏度变化也可应用式（15）确定。本文随后的敏感性分析皆基于图3数据。

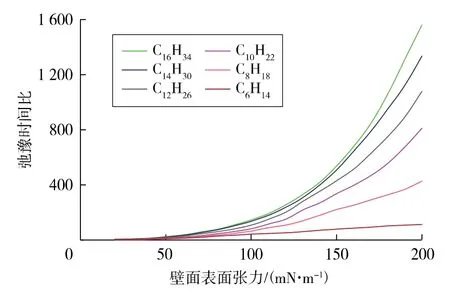
图3 不同烷烃分子弛豫时间比随壁面表面张力的变化

3.1 壁面表面张力对增长因子的影响

随着壁面表面张力增加，流体-固体作用力随之增强，导致边界层流体弛豫时间及其黏度随之变大，固体壁面性质对烷烃传输能力有显著影响（见图4）。由图4可以看出，随着壁面表面张力的增加，增长因子逐渐减小，说明强壁面表面张力条件下，烷烃分子流动性显著下降（C16的增长因子变化可达4个数量级）。

图4 增长因子与壁面表面张力的关系

当壁面表面张力大于50 mN/m时，增长因子不再有明显变化，可解释为当壁面表面张力较强时，边界层流体黏度显著增加，其滑移现象为负滑移，导致增长因子小于1，而在壁面表面张力较低条件下，流体-固体作用力较弱，边界滑移现象为正滑移。同时，随着碳链长度变长，增长因子变大，说明微尺度效应对长链分子的影响更明显。这是由于近壁面处的长链分子更容易在壁面作用力下出现层状排列，而体相部分相邻层长链分子互相缠结，导致体相部分相对边界层流体分子流动性明显降低。

3.2 孔隙半径对增长因子的影响

页岩油储层中孔隙结构较为复杂，且有机孔发育，因此有必要对不同孔隙半径有机孔（壁面表面张力23.2 mN/m）中的流体传输机理进行研究（见图5）。当孔隙半径逐渐变大，微尺度效应的影响降低，这是由于壁面层对烷烃分子的影响有限，约为2个分子层的厚度。当孔隙半径增大时，边界层占比降低，增长因子逐渐减小。当孔隙半径大于50 nm时，对于碳原子数小于14的烷烃分子，其微尺度效应可以忽略。当碳原子数较大时（如C16），微尺度效应的影响更为明显。当孔隙半径大于250 nm时，其微尺度效应方可被忽略。这说明在计算页岩油藏渗透率时，需考虑微尺度效应及流体分子结构的影响。

图5 增长因子与孔隙半径的关系

3.3 壁面粗糙度对增长因子的影响

真实孔隙壁面往往有较多的粗糙单元，具体大小难以表征，但通过适当调整其参数值，可以较好地用于拟合、预测实验数据。同时，粗糙单元的存在可以改变表面润湿性，从而使得流体流动性发生变化。由于烷烃分子表面张力较小，在相对较高的固体表面张力条件下，油分子往往可以润湿固体表面，即油分子接触角小于90°。在这种条件下，壁面越粗糙，油分子润湿能力越强，滑移长度降低，表现为壁面粗糙度分形维数越大，增长因子越小（见图6）。

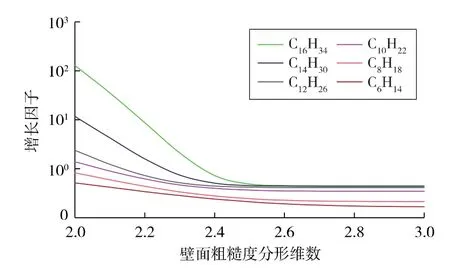
图6 增长因子与壁面粗糙度分形维数的关系

3.4 应力及弹性模量对增长因子的影响

孔隙所受应力及其力学性质对流体应力敏感程度有明显影响，尤其当孔隙半径较小时，应力敏感条件下的孔径变化将使微尺度效应更为明显。孔隙所受应力及弹性模量对增长因子的影响见图7，其泊松比为0.04。由图7可知：随着孔隙所受应力增加，增长因子逐渐减小；当弹性模量增加时，变形量减小，应力敏感程度减弱。

图7 不同弹性模量条件下增长因子与应力的关系

3.5 泊松比对增长因子的影响

由图8可以看出，泊松比对微尺度流动过程中的应力敏感现象有显著影响。相同弹性模量条件下，泊松比越大，应力敏感程度越小，增长因子逐渐增加。这是由于泊松比是表征横向变形的系数，同一弹性模量条件下，泊松比越大，毛细管受压伸长，其相对变形量逐渐减小，应力敏感性降低。

图8 不同弹性模量条件下增长因子与泊松比的关系

3.6 黏度变化对增长因子的影响

有机孔中流体-壁面作用力较弱，边界层原油分子流动性较强，但流体-壁面作用力导致毛细管中的黏度分布不均匀，使得微尺度下烷烃分子流动性显著降低。由图9可知：对正十六烷（C16H34)来说，考虑黏度变化时，其增长因子仅为忽略黏度变化时的68%～88%；而对于正己烷（C6H14)，尽管流体-壁面作用力导致其边界层流体黏度显著变化，但由于其较小的滑移长度，导致黏度对增长因子的影响较小。这说明在页岩油微尺度流动模拟计算过程中，需在考虑原油分子结构的基础上，决定是否考虑黏度变化的影响。一般情况下，黏度变化的影响可以忽略，而对于长链分子，忽略黏度变化的影响将导致结果出现较大误差。

图9 不同孔隙半径条件下黏度变化对增长因子的影响

4 结论

1）本文建立的页岩有机质纳米孔传输模型，考虑了分子结构、温度、壁面粗糙度及应力敏感的影响，可用于微尺度流动机理模拟，并推广应用于页岩油藏渗透率计算。

2）页岩油传输能力与分子结构、孔隙半径、孔隙类型、壁面粗糙度有关：碳链长度及孔隙类型起主导作用，微尺度效应对长链分子传输能力有显著影响；当孔隙半径大于250 nm，微尺度效应的影响可被忽略，但同时考虑到页岩油藏纳米孔发育，进行模拟计算时仍需考虑微尺度效应的影响；随着壁面粗糙度增加，烷烃分子对孔隙壁面的润湿能力变强，导致传输能力下降。

3）页岩油微尺度传输机理与力学性质密切相关，且弹性模量越大，孔隙可压缩性减小，应力敏感程度越弱；泊松比越小，微尺度传输能力变化幅度越大，应力敏感程度越强；有效应力越大，孔隙变形程度越大，应力敏感性增强。

4）微尺度条件下，强流体-壁面作用力导致的孔隙中黏度分布不均匀是页岩油微尺度流动过程中的主要影响因素，忽略黏度变化将导致计算误差。

5）本文未考虑页岩有机质丰度、混合润湿、有机质吸附和解吸附的影响，进一步需开展的研究有：考虑混合润湿及有机质吸附条件下的页岩油传输模型；将微尺度模型扩展至岩心以及油藏尺度；不同截面形状、非光滑壁面的影响；微尺度效应对页岩油藏产能的影响。