考虑前车效应的一维元胞自动机混合交通流模型研究

张锦，符鼎俊，李启朗

（安徽建筑大学 数理学院，安徽 合肥 230601）

随着计算机技术的发展，在交通工程领域计算机模拟技术的应用越来越广泛，通过计算机对交通流的模拟，人们可以在计算机上动态地仿真交通流中的各种现象以及交通流的交通特征并应用于交通规划以及交通管理。此外，利用计算机模拟技术可以避免进行一些费用昂贵且周期长的交通调查和现场试验，在付出较低成本的情况下就可以收集难以获得的数据，并再现各种交通现象，可以从一个崭新的视角展开对交通问题的研究。由于交通系统中的数据是极为复杂且庞大的，一般的离散方法和微分方法都不适宜进行交通计算和仿真，而元胞自动机的规则简单和快速的计算能力在交通仿真中发挥了重要作用，进而，元胞自动机在交通系统中得到了更为广泛的应用。

在Nagel 和Schreckenberg 提出的元胞自动机模型（简称NS 模型）的基础上，人们提出了很多改进过的模型，开始考虑了前车对于随机慢化行为的影响，如梁经韵等针对多路段特点提出的多路段元胞自动机交通流模型，张柠溪等考虑到前车速度与高速跟驰现象，提出的考虑动态车间距的一维元胞自动机交通流模型以及侯培国等人考虑驾驶员行车过程中进行防御性驾驶，即驾驶员当发现前车减速并且下一时刻停车时，提前进行防御性减速的基于防御性驾驶的一维元胞自动机交通流模型，Newell提出了一个车辆跟驰模型（Newell模型），模型中车辆的速度是时刻之前车间距的函数。随后，在Newell 模型的基础上，Bando 等人提出了优化速度模型（optimal velocity model，OV），Helbing和Tilch 使用经验数据来校准优化速度模型（OV 模型），发现优化速度模型会出现过度加速，不合理减速和碰撞等现象。他们认为，当前车的速度比后车的速度小的时候，需要考虑到前后车速度差的影响，于是他们提出了广义力模型（general force model，GF）。本文提出的元胞自动机交通流模型在Velocity-Dependent-Randomization模型（VDR 模型）的基础上进行了扩展，VDR模型的慢启动规则应用较为广泛，其目的是为了研究高速公路上的“幽灵堵塞”，VDR 模型也可以运用于研究交通亚稳态现象，为了模拟出明显的亚稳态现象，VDR 模型将下一时步静止车辆的随机慢化概率取值0.75，运动车辆的随机慢化概率取值1/64，与实际驾驶情形相比，这个取值偏差很大，使得VDR 模型容易失去稳定性，当道路系统中连续的车辆速度同时降低为0 时，会立刻出现大规模堵塞。新模型的随机慢化概率不再是依赖于车辆速度，而是连续两辆车之间的速度差，随机慢化的减速幅度也是根据前车的速度差进行选择。与传统的VDR 模型相比，系统中不会出现大范围的宽运动阻塞。实际交通中，车道上一般都是由不同类型不同性能的车辆混合行驶，因此研究混合车辆的交通流问题更能反映真实交通的特性。新模型的研究对象为混合交通流，车长不再是固定的1 元胞，而是存在两种类型的车辆，大型车辆（2 元胞）与小型车辆（1 元胞），以往的混合交通流模型只研究了不同车型最大速度上的差异及随机慢化概率上的差异或是车辆长度对交通流的影响，没有考虑不同车型存在着不同的加速模式，新模型模拟了两种不同车型不同的加速模式。本文提出的新慢启动模型中，考虑了前车的期望速度，通过前车的影响以避免紧急制动并以此计算出前车在下一时步的期望间距，根据两辆连续车辆的速度差调整车辆随机慢化的概率以及减速幅度，加速模式由不同车辆类型决定，对单车道混合交通流进行了模拟，并对车速及加速度进行了分析。

1 新慢启动模型

Step1 确定随机慢化概率及减速幅度：

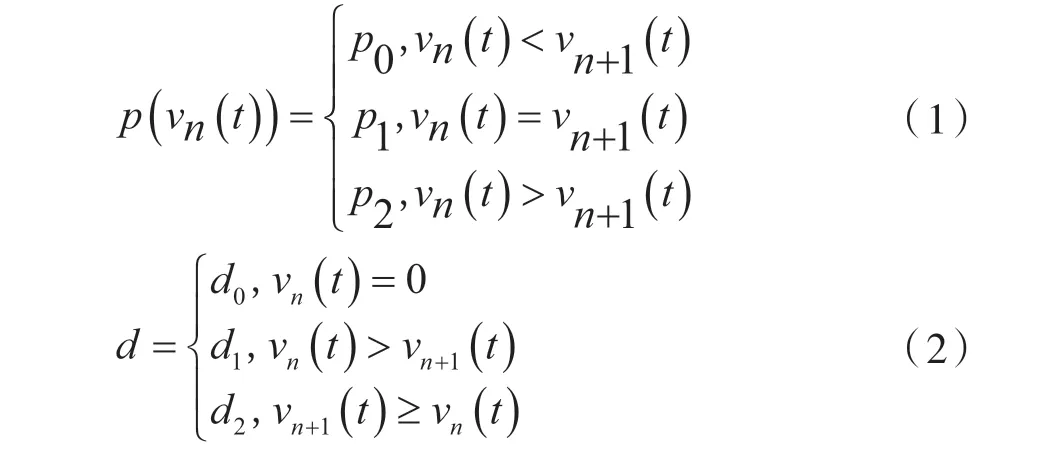
Step2 加速：当l=1 时

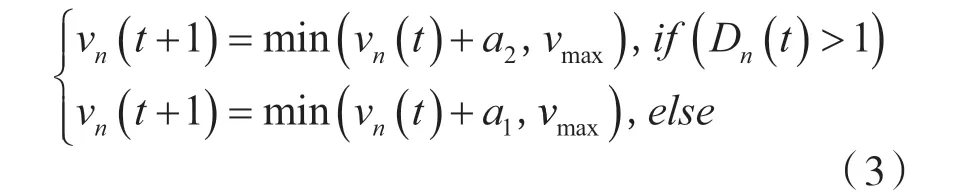
当l=2 时

其中D（t）=x（t）-x（t）-l，l为车辆长度，x（t）与x（t）分别为n+1 号车和n 号车t 时刻的位置；

Step3 减速：

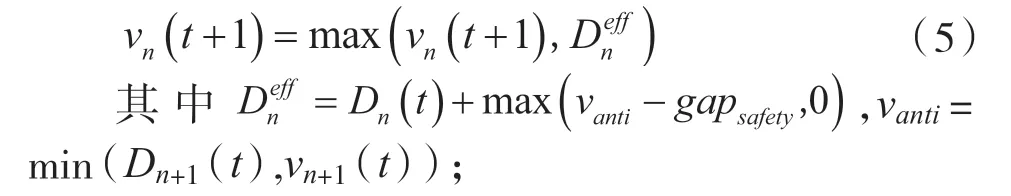
Step4 随机慢化：以概率P（v（t））令

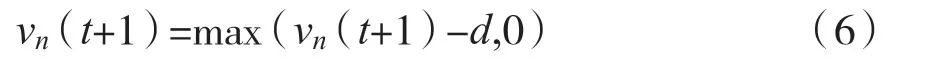
Step5 位置更新：

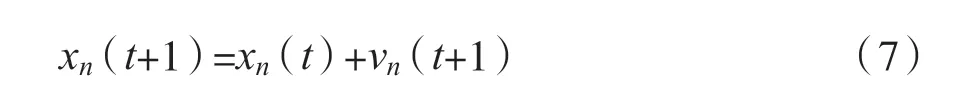
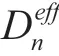
2 数值模拟结果与讨论

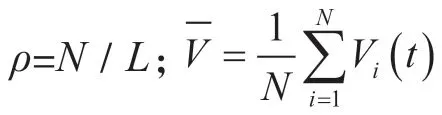
2.1 基本图

图1（a）与图1（b）分别为NS 模型（慢化概率ρ=0.6）与新模型使用表1 中的参数进行模拟得到的基本图，在NS 模型中大型车辆占比的增加只会对流量产生微弱的影响，与NS 模型相比，从图1（b）中可以看到，新模型的最大流率是明显大于NS 模型中的，并且随着道路中大型车辆占比的增加，临界值O会逐渐增大，最大平均流量也会随着大型车辆占比的增加逐渐下降。新模型中基本图会分为三个部分，以大型车辆占比为0.5（L=0.5）时为例，最左边的部分（0 ＜O＜O），此时道路处于低密度状态，流量都是随着占有率的增加线性增长的，最右边的部分（O＜O ＜1）此时道路处于高密度状态，道路趋于堵塞，流量随着占有率的增加线性减少，中间部分（O＜O ＜O），由于考虑了前车的速度效应以及减速幅度及随机慢化的调整，提高了交通流的稳定性，消除了减速中的过度行为，形成了流量随着道路占有率缓慢下降的波动曲线。当系统中不存在大型车辆的时候（L=0.0），道路占有率与流量的曲线存在着两个峰值。为了了解随机慢化概率的调整对模型的影响，分别选取了三组不同的慢化概率进行了模拟，模拟结果如图2（a）即忽略了当前车辆车速小于前车车速的情况，可以发现当道路占有率超过临界值O后，流量会随着道路占有率的增加线性下降，即考虑前车效应可以提高中高密度区域的流量。接着调整了控制预期效应的参数gap，令gap=2，这样降低了前车预期的有效距离，驾驶行为也变得更加保守，保守的驾驶行为会减少大幅度的减速，模拟结果如图2（b），其流量在前期是低于原模型的，当道路占有率为O时，调整后的模型才会达到流量的峰值并且两条曲线合并，即之后随着道路占有率的增加，流量的下降趋势都是相同的，gap的影响仅存在于低道路占有率的情况下。

表1 模型参数

图1 NS 模型与新模型在不同大型车辆占比下的数值模拟基本图

2.2 时空图及速度特征分析

时空图由数据坐标点构成，其中横坐标为车辆的位置，纵坐标代表系统中的时刻。道路长度为2000 个元胞，选取了前1000 个元胞展示时空演化特征，从图1（b）中可以看到当L=0.5 时随着道路占有率的增加，流量的变化会呈现出三个模式。当道路占有率低于O时，此时处于自由流状态，流量随着道路占有率的增加线性增加，我们选取（0＜O ＜O）中的任意一点O=0.15，模拟得出的时空图如图3 所示。图3（a）为O=0.15 时的时空图，可以看出图中基本上没有阻塞区域，由图3（b）的热力图也可以看出，系统中绝大部分车辆都保持高速行驶（红色区域代表高速，不同颜色代表不同车速），只有少数车辆会根据规则（4）随机慢化降低车速，由于考虑了前车效应，大大减少了道路系统中车辆因为保持安全距离的过度减速。将图3（a）、图3（b）分别与图4（a）、图4（b）相比（图4 为当道路占有率为0.15 时NS 模型的时空演化图），在同样的道路占有率的情况下，新模型道路系统中的大部分车辆都是高速行驶，并且没有大范围的阻塞区域，反观NS 模型中由于随机慢化造成的减速会产生一条阻塞波并随着时间推移向上游传播，并且阻塞区域存在着大量的低速车辆。图5 是NS 模型与新模型在O=0.15（L=0.5）时的速度统计，新模型避免了过度的减速，从而阻止了系统中阻塞波的形成，系统中高速车辆占比大于NS 模型，能更大程度还原现实交通流中低密度时的运行模式，交通系统也更加稳定。

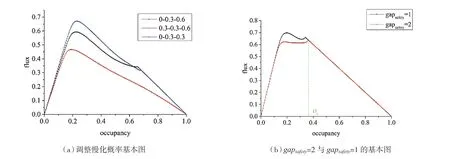
图2 Lvo=0.5 时调整参数模拟结果对比

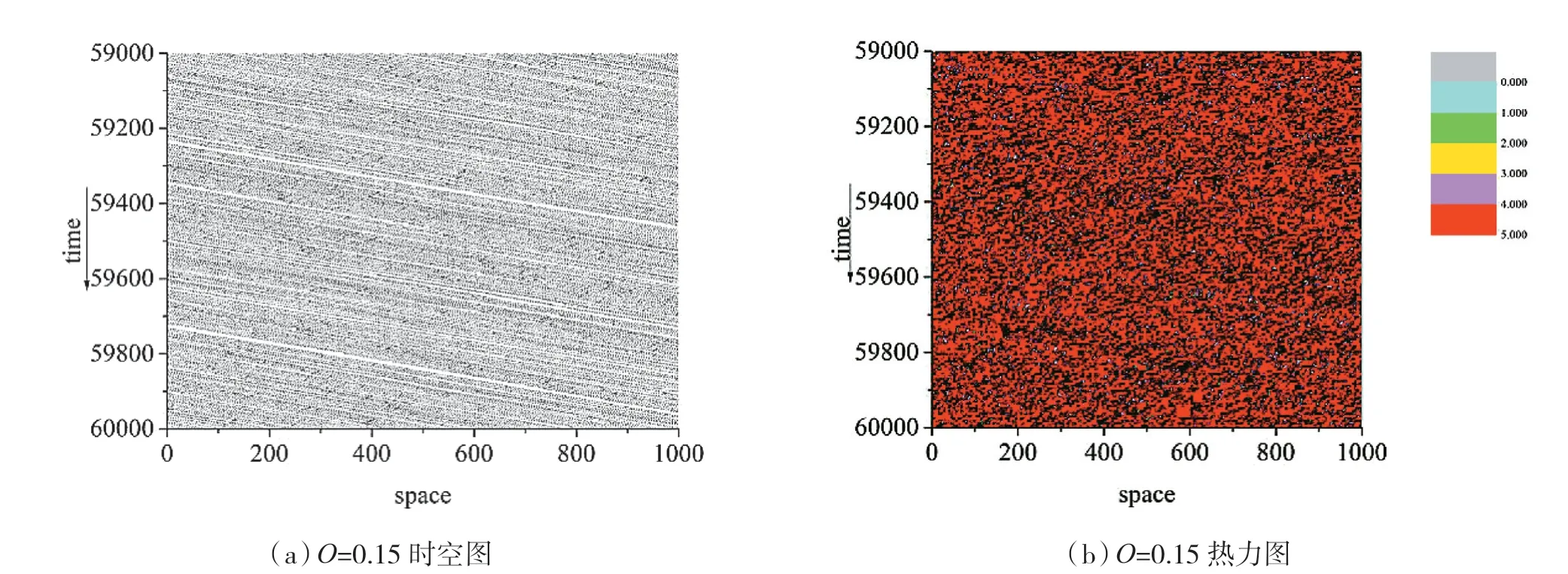
图3 当道路占有率为0.15 时新模型的时空演化图

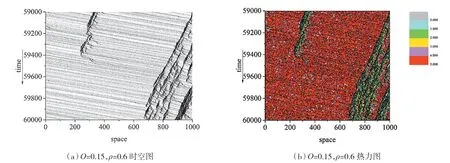
图4 当道路占有率为0.15 时NS 模型的时空演化图

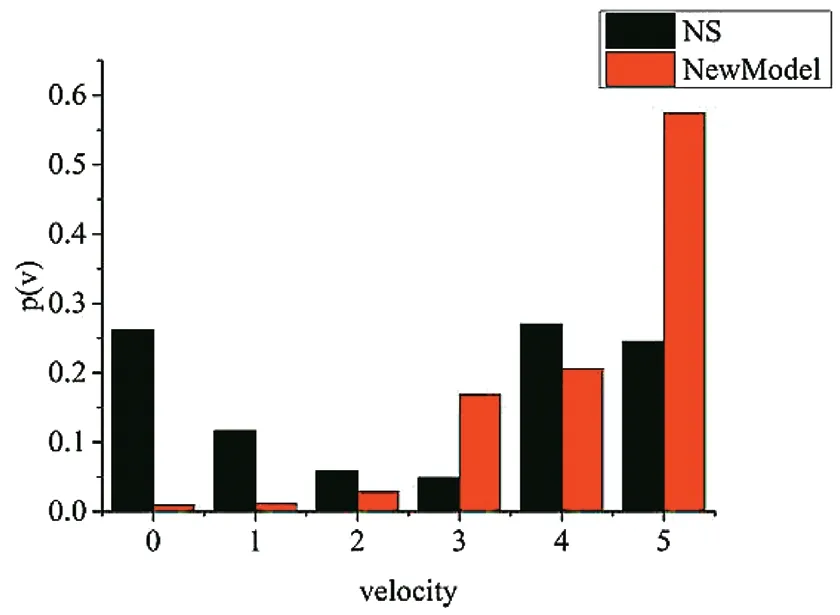
图5 当道路占有率为0.15 时NS 模型与新模型的速度统计

在中间部分任选一点O=0.40，时空图如图6（a）所示，随着道路占有率的增加，没有宽运动阻塞的形成，从图6（b）中可以看出道路系统中只是出现了大面积的低速区域，说明了新模型中的自适应系统加速了阻塞的消散，不会形成大范围的阻塞，提高了中高密度区域的流量。在最后一部分，当O=0.80 时，时空图如图7 所示，由图7（b）的热力图演示可以看出，此时系统中只剩下了停止与低速车辆，在图7（a）的时空图中，可以观察到数条狭窄的阻塞带，即图7（b）中的灰色区域，以往的慢启动模型会出现大范围的宽运动阻塞带，新模型与其存在着很大的不同，表明了新模型更好地再现了现实交通系统中，车辆处于堵塞中的启停模式，模拟结果贴近真实系统中的车辆时走时停的现象。图8 为当L=0.5 时道路占有率处于不同值情况下的加速度统计，可以清楚地看出考虑了前车的速度状态，减少了为了避免碰撞产生的强减速行为，加速度最多分布于1、0、-1 这三个值，反映出了交通流状态相对其他模型更为平稳，更加精准地还原了现实交通系统中的加速与减速行为。

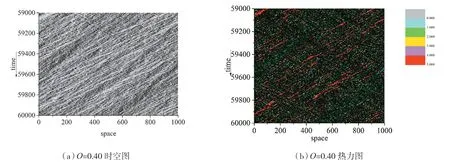
图6 当道路占有率为0.40 时新模型的时空演化图

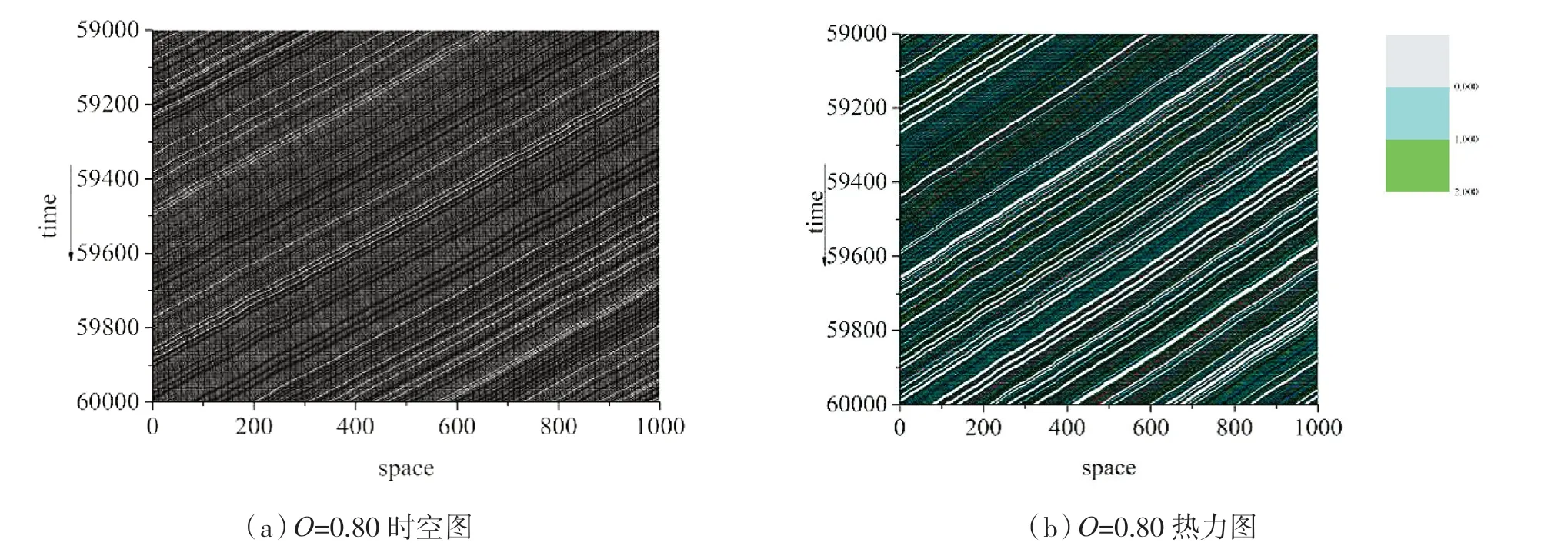
图7 当道路占有率为0.80 时新模型的时空演化图

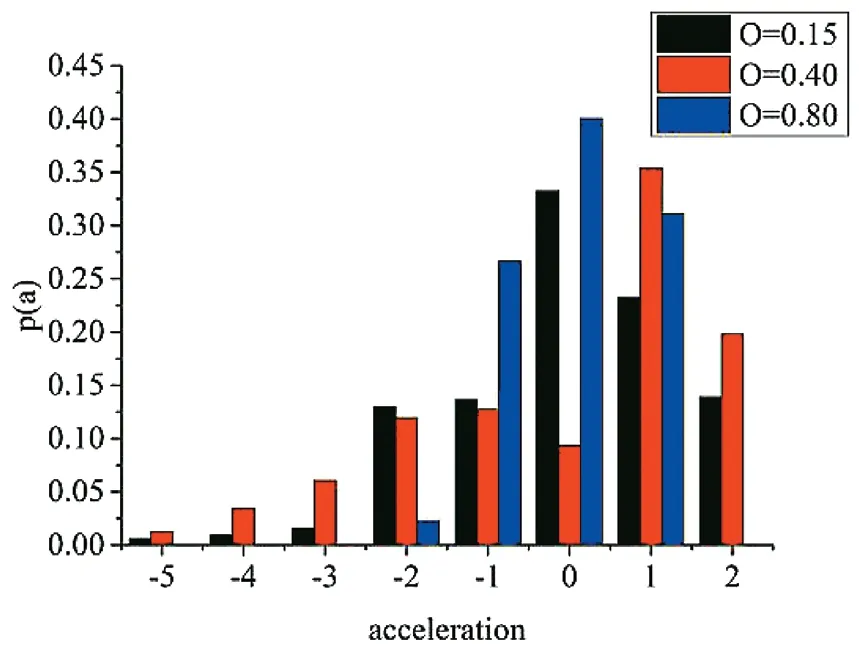
图8 Lvo=0.5 加速度统计

3 结论

本文研究了一个新的元胞自动机混合交通流模型，在NS 模型的基础上结合了慢启动模型思想，考虑了不同车型加速行为的差异以及连续两辆车之间速度差异对慢化参数的影响，通过仿真发现新模型有以下几个特点。首先模拟的基本图显示流量密度曲线被分割成三个区域，不再是简单的线性关系，考虑了周围的交通环境，模拟结果能更好地再现交通流特征；长车占比与最大平均流量以及道路占有率的临界值有着密切的关系，当道路密度越大时，长车占比对于系统的影响越大。其次，减少了车辆行驶中不必要的减速行为以及紧跟前车的行为，提高了系统的通行能力，从而抑制了阻塞的形成；与其它模型相比，模型提高了中高密度区域的流量并且可以长时间保持均匀的流量，从而具有较高的交通效率。最后，结合VDR 模型的思想，考虑了不同的减速幅度，更加贴近现实驾驶行为，提高了系统的稳定性，阻塞形式得到了改变，促进了大集团阻塞的消散，小阻塞集团可以稳定存在于道路系统中，解决了VDR 模型与实际驾驶相差较大的问题。