基于有限元仿真的冰箱搁架玻璃厚度估计算法

程旺，张谷峰，梁龙旭，常见虎

（合肥美的电冰箱股份有限公司，安徽 合肥 230601）

冰箱玻璃搁架以钢化玻璃为主体，用于存放瓜果蔬菜及饮料等，位于箱体内醒目位置。玻璃搁架若设计太薄，承载时搁架变形严重，影响用户使用体验。若设计太厚，用户拆装不方便，同时材料和包装费用增加，不利于成本控制。相关设计标准仅约束玻璃的许用厚度值，选择条件较粗糙，不利于设计人员定型，导致部分玻璃搁架变形过大。

目前针对玻璃研究的关注点是玻璃的应力、损伤及爆裂问题，因设计冰箱时，可选的玻璃厚度已满足爆裂的相关要求，相关实验对玻璃搁架的加载力低于玻璃破裂极限值，因此不考虑玻璃搁架破裂问题。冰箱玻璃的承载力研究已取得一些进展，得出影响承载力的因素主要是玻璃搁架的对角线及厚度尺寸，但如何确定玻璃厚度未做探讨。本文通过对玻璃搁架承重进行有限元分析，开发出玻璃厚度选优软件，为设计人员快速选型提供依据。

1 实验方法

冰箱在实际使用过程中，搁架上的物品摆放重量、种类和分布位置等完全随机，无法在实验室模拟真实使用场景。针对以上问题，制定以下试验标准：

（1）物料种类：测试台、测试样机、砝码、游标卡尺。

（2）测试过程：将测试样机摆放在测试台，测量空载时搁架底端与基准的垂直间距，记录3 组数据，取均值。然后将24 kg 砝码沿深度方向中心线按1 列N 排堆放（如图1 所示），重复上述测量并记录3 组数据，取均值。砝码直径Φ80 mm，单个重1 kg 或0.5 kg。

（3）数据分析：将空载和负载下数据相减，取均值，即为变形量。

（4）注意事项：

●堆放砝码时砝码不允许悬空，不能压住前后饰条：

●搁架深度在280-340 mm 之间，摆放3 排砝码，每排8 kg；

●搁架深度在360-420 mm 之间，摆放4 排砝码，每排6 kg；

●搁架深度在440-460 mm 之间，摆放5 排砝码，前4 排每排5 kg，第5 排4 kg；

图1 玻璃搁架测量方法

2 分析验证

2.1 有限元模型

有限元分析是以计算数学、计算力学及相关工程科学为基础，针对复杂工程或产品进行数学建模、计算分析、行为模拟及优化设计的计算机信息处理技术。静载荷作用下的结构，需要求解的基本有限元方程实际是外力和内力的平衡方程，可以表示为

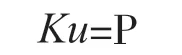
式中，K 为结构的刚度矩阵（各个单元刚度矩阵的组合），矢量u 为位移向量，P 是作用在结构上的载荷向量。其求解思路是：通过将几何体离散成有限多个连续的单元体，单元和单元间通过节点连接。按静力等效原则将作用在结构体上的外部载荷分解成等效节点载荷向量，把需要在复杂的连续弹性体上分析计算的问题，转化为对一个多元代数方程求解的过程。上述几何离散及方程求解是非常复杂和困难的过程，为解决此问题，专业的ANSA 和Hypermesh 和等前处理软件，以及ABAQUS、ANSYS、NASTRAN 等大型通用分析软件应运而生。玻璃搁架堆码实验即为静载荷作用下的结构，本文的玻璃搁架有限元模型即采用Hypermesh 进行建模。

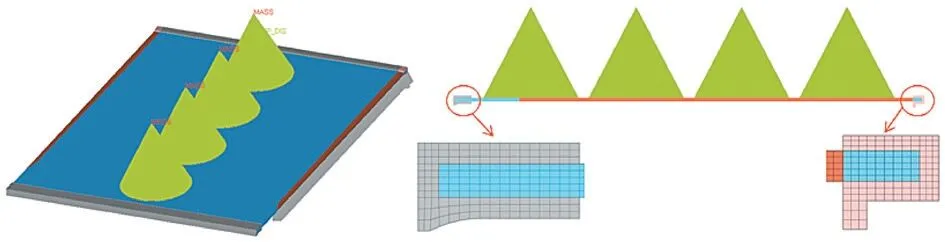
图2 玻璃搁架仿真模型

为保证分析精度，玻璃及前后饰条采用实体单元建模，模型尺寸与形状以实际玻璃搁架为准，网格数量在300 万以内，建立的有限元模型如图2 所示。其中：长度和宽度方向网格基本尺寸1 mm；玻璃厚度方向划分5 层网格，网格尺寸由玻璃厚度确定；前后饰条厚度方向划分3 层网格；删除玻璃边框及饰条上小于0.5 mm 的圆角；玻璃和饰条共节点；玻璃弹性模量72000 MPa。将砝码简化成位于质心位置的质量点，单元质量为每排砝码实际重量，质量点与玻璃相应节点耦合连接。模型中，约束左侧玻璃底面最外侧一列节点的全部自由度，只约束右侧玻璃底面最外侧一列节点的垂直自由度，模拟搁架在箱体内的固定情况。

2.2 模型验证

随机选择9 种玻璃搁架进行堆码实验，测量搁架几何尺寸及变形结果。按实际测量所得搁架尺寸，在Hypermesh 中建立对应的有限元模型，并进行仿真分析。在后处理软件中提取搁架的最大变形量、查看如图3 所示的变形云图等。图示玻璃搁架尺寸为461×270×3.2（单位：mm），其中红色为变形量最大区域，颜色梯度反映了不同变形量的大小，搁架变形量从中间往两端递减。

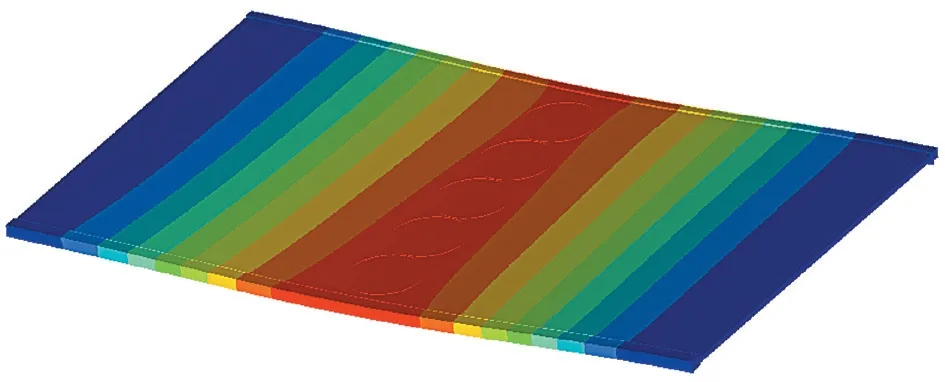
图3 玻璃搁架变形云图

分析假设不同厚度、不同批次的玻璃弹性模量相同，箱体不存在变形。模型同时忽略了胆筋（搁架支撑）宽度和长度对搁架变形的影响，只将胆筋宽度和搁架外伸长度设成定值。实际中，胆筋宽度和长度对搁架变形的影响存在一定影响。9 种玻璃搁架实验与分析结果如表1 所示。其中，分析与实验误差均在6%以内，表明现有模型可近似模拟出实验变形值。

表1 实验与分析结果对比表

3 影响因素与公式拟合

冰箱在设计过程中，整体箱体尺寸和壁厚，以及风道等相关尺寸一旦确定，玻璃搁架的宽度和深度也随之确定。此时需根据搁架宽度和深度值，确定玻璃的厚度。因冰箱标准化的要求，玻璃搁架的深度、宽度及厚度的取值范围如下：

（1）搁架深度：取值在205 mm 至505 mm 之间。搁架过浅，盛放物品有限；搁架过深，不便于取放物品。

（2）搁架宽度：取值在300 mm 至800 mm 之间。搁架过窄，不满足盛放需求；搁架过宽，冰箱尺寸过大。

（3）玻璃厚度：因标准化需求，玻璃可选厚度只有3.2、4、5、6 mm 四种厚值。若厚度过薄，玻璃破碎性能达不到要求；厚度过厚，拆卸不便，成本过高。

在上述深度和宽度范围内，如何确定玻璃厚度，进而影响承载时搁架的变形量，是判定厚度选择是否合理的根本。因此须确定搁架深度、宽度和厚度对变形量之间的大致关系，为后续详细分析提供依据。

3.1 敏感度分析

（1）搁架深度

为确定搁架深度对变形的影响，将搁架宽度和玻璃厚度均设成定值，其中宽400 mm，厚3.2 mm。搁架深度采用300/398/460 mm 三种值。三种深度下玻璃搁架变形量如图4（a）所示，变形趋势表明，搁架深度与变形量成反比，深度越大，变形量越小。搁架深度从300 mm 增至460 mm，变形量由5.5 降至3.8 mm，降幅较小，深度对变形影响较小。

（2）搁架宽度

将搁架深度和玻璃厚度均设成定值，其中深300 mm，厚4 mm。搁架宽度采用300/400/500/600/700/800 mm 六种值，变形量如图4（b）所示。变形趋势表明，搁架宽度与变形量成正比，宽度越大，变形量越大。搁架宽度从300 mm 增至800 mm，变形量由1.3 增至24 mm，增幅较大，宽度对变形敏感。

（3）玻璃厚度

将搁架宽度和深度均设成定值，其中宽600 mm，深300 mm。玻璃厚度采用3.2/4/5/6 mm 四种值，搁架变形量如图4（c）所示。变形趋势表明，搁架厚度与变形量成反比，厚越大，变形量越大。玻璃厚度从3.2 mm 增至6 mm，变形量由18.3 降至3.5 mm，降幅较大，厚度对变形敏感。

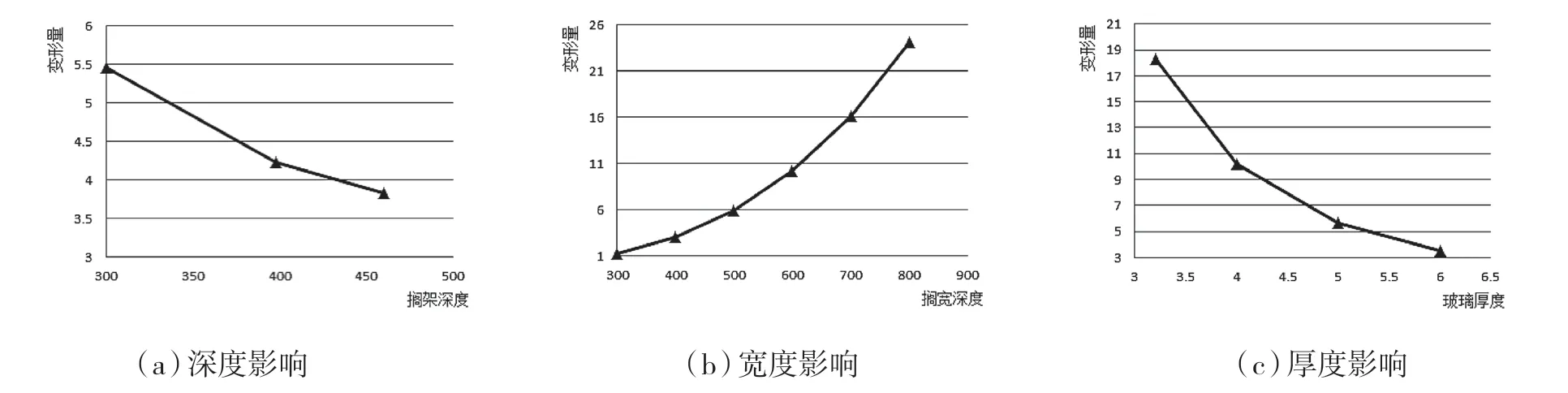
图4 变形趋势

图5 玻璃搁架变形曲线

3.2 拟合公式

为拟合出搁架变形的精确计算公式，根据影响搁架变形的敏感度结论，建立以下模型：

（1）因搁架深度对变形影响较小，模型深度仅设定300/398/460 mm，共3 个变量。

（2）由于搁架宽度对变形敏感，须对宽度进行详细研究。模型宽度从300 增加至800 mm，每增加20 mm 计算一次，共26 个变量。

（3）基于玻璃厚度对变形敏感的结论，对涉及搁架厚度全部计算，计4 个变量。

上述模型涉及3 个搁架深度、26 个宽度、4 个玻璃厚度，共312 个模型（3×26×4=312）。将分析结果进行整理，获得12 条不同深度、宽度及厚度的变形关系曲线，如图5 所示。图通过插入与上述曲线相近的趋势线，可得不同深度下，宽度与变形量之间的计算公式，即拟合公式。如345 mm ＜玻璃深度≤425 mm，玻璃厚3.2 mm，宽度与变形量之间的拟合公式为：

Y=7×10X+7×10X-6×10X+0.0021X-0.208

式中X 轴为宽度值，Y 轴为变形量。

图中每条变形曲线可得一个拟合公式，共计12 个公式，按照玻璃深度进行分组，供后续软件编制使用。

随机选择30 种玻璃搁架进行堆码实验，测得其变形结果。然后根据玻璃搁架尺寸，选择相对应的计算公式，得到推导变形量。各种玻璃搁架实验变形量及推导变形量误差区间如图6 所示。

对比结果表明，实验结果与推导结果误差在8%范围内，最大误差为7.2%。因行业现有标准未规定搁架允许的变形量，也未涉及分析误差大小，经相关设计和实验人员讨论后，公式所得变形量可替代实验，计算结果已满足设计人员需求。

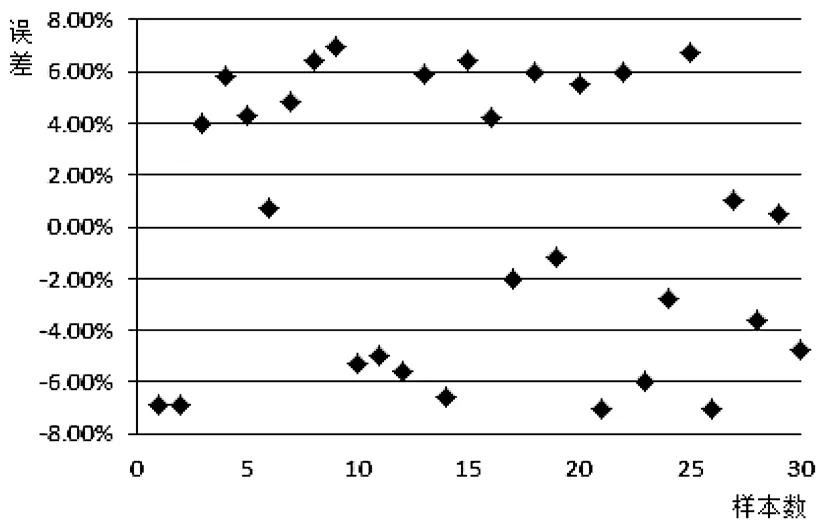
图6 误差区间分布

4 程序设计

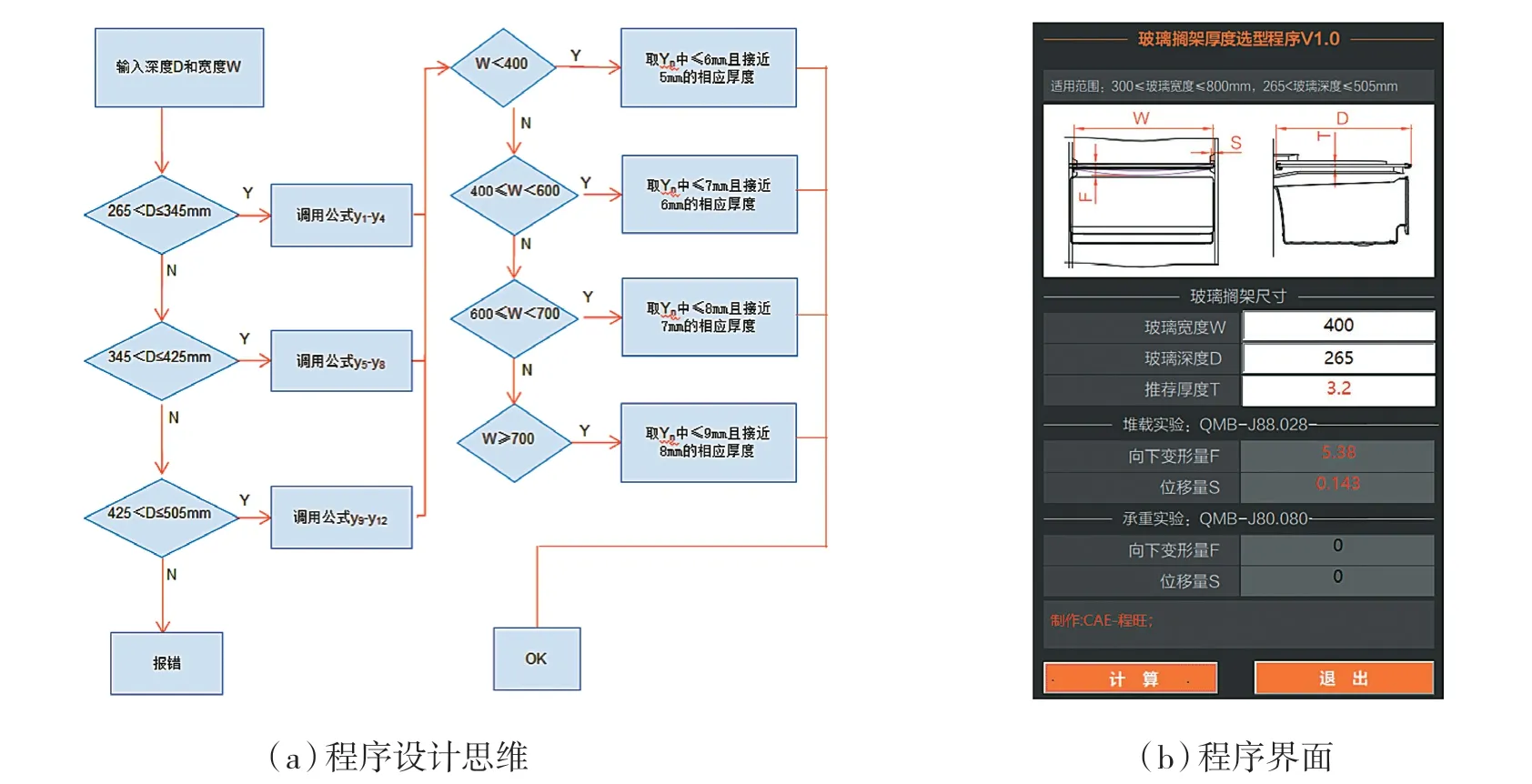
图7 程序设计思维图和程序界面

根据上述拟合公式，使用Microsoft 公司开发的一种基于对象的程序设计Visual Basic（VB）语言编制。VB 拥有图形用户界面（GUI）和快速应用程序开发（RAD）系统，提供了大量可视化设计工具，可帮助使用者快速建立一个应用程序。编制软件时，以上述12 个拟合公式为基础，编写思维如图7（a）所示。首先在GUI 界面创建以图形呈现的各种菜单及命令对象，并设计这些对象的属性。然后再编写功能模块的代码，使软件实现以下功能：

（1）使用权限判断：根据IP 地址，如果是允许端口则正常启动软件，如果不是则出现警告并无法使用；

（2）玻璃厚度和深度输入范围判断：当输入的宽度或深度在限定范围，正常计算。若超出范围，会自动提示输入超限；

（3）玻璃厚度推荐值输出；

（4）变形量和位移量输出。

玻璃搁架厚度选型程序界面如图7（b）所示。示例中输入的玻璃宽度为400 mm，玻璃深度为265 mm，程序推荐使用3.2 mm 厚玻璃，此尺寸下玻璃搁架承载24 kg 砝码时向下变形5.36 mm。该程序使设计人员不需要掌握深奥的力学理论知识，只需在软件界面中输入玻璃宽度和深度，即可快速得出玻璃优选厚度及相应厚度下的变形量。

5 结论

本文根据冰箱抽屉以及使用实验方法，对9 款玻璃搁架进行堆码实验，并根据实验结果，修正有限元模型，使仿真能够准确模拟出玻璃搁架的实际变形。通过仿真，确定搁架宽度和玻璃厚度为影响变形的主要因素。然后建立覆盖所有搁架尺寸的312 个有限元模型并进行仿真分析，得到搁架变形的计算公式。通过随机选取30 款搁架实验结果及公式计算结果进行对比，证明公式计算结果的准确性。最后根据所得12 个计算公式开发出计算程序，通过输入玻璃宽度和深度，迅速得到推荐厚度以及此厚度下的搁架变形量，该方法对设计人员的选型提供了理论依据。