高桩低应变测试的交错网格有限差分法响应分析

姜静，卢志堂，高子杰

（1.宣城职业技术学院 电大工作处，安徽 宣城 242000；2.合肥工业大学 资源与环境工程学院，安徽 合肥 230009；3.安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230022）

随着我国经济建设的高速发展，桥梁工程及沿江城市建设得到快速发展，高桩越来越被广泛运用于桥梁、港口码头及工业与民用建筑等工程中。与低桩相比，高桩上部分是出露于土壤的，这必然使得在对其进行低应变完整性检测时的三维干扰增加，最终导致检测结果分析的难度增加。因此，研究高桩的低应变检测问题是十分必要的。

Steinbach等于1975 年首次提出应力波传播法检测混凝土桩和沉箱质量。之后，该方法被广泛运用于基桩检测。Van Koten等利用了函数代换和求解黎曼函数的方法得到了均质土中无限长桩的时域纵向响应。在此基础上，王奎华等求得了有限长桩及弹粘性桩的受迫振动问题的解析解。刘东甲运用差分法得到了完整桩模型，且直观的反应了桩中应力波的传播过程。同时，刘东甲运用Laplace 变换及矩阵理论解析地求得缺陷桩的桩顶传递函数，并得到了桩顶速度频响函数等。Jiang采用交错网格差分法对承台-桩系统进行了研究，并获得了承台表面最佳拾振位置及各参数对承台表面速度曲线的影响。然而，以上研究的都是浅桩基础或者全埋入的桩基。

余云燕等采用回传矩阵法研究了半埋入基桩的瞬态响应，得到了桩顶速度响应并分析了桩土参数对桩顶速度曲线的影响。但是，目前基于一维基础上进行的研究，不能真实地反映出高桩的三维效应。为了研究高桩的三维效应及如何避免三维干扰，本文采用交错网格差分法在三维轴对称条件下对高桩低应变检测问题进行了相关研究。

1 计算模型和理论公式

1.1 计算模型

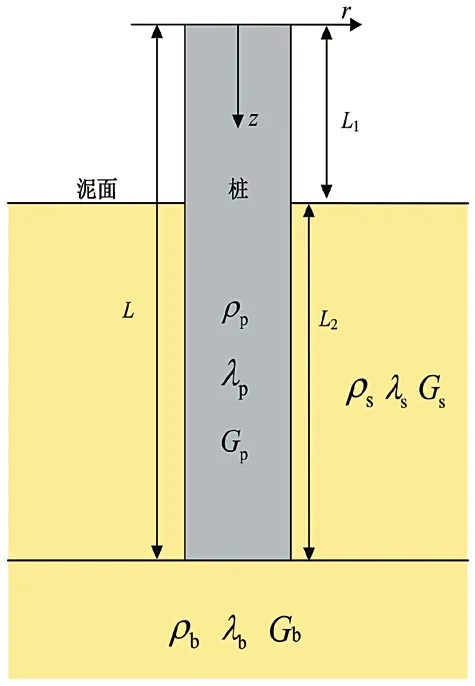
图1 高桩计算模型

首先建立高桩模型，如图1 所示。下部分桩身埋入土壤中，而上部分出露于土壤。其中桩长为L，半径为R，外露桩长为L，入土深度为L。桩身密度和拉梅常数为ρ、λ、μ，桩侧土的密度和拉梅常数为ρ、λ、μ，桩底土的密度和拉梅常数为ρ、λ、μ。

1.2 弹性波动方程

假设桩体和土都是各向同性弹性体，并且不考虑体力。在低应变动测条件下，桩土界面不分离，桩土界面处速度和应力具有连续性。基于弹性理论，二维弹性波动方程如下：

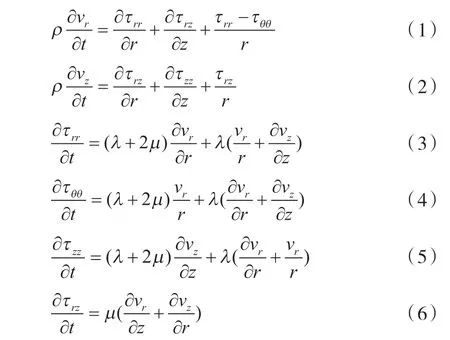
式中，ρ 是弹性体的密度，λ、μ 是弹性体的拉梅常数。τ、τ、τ分别表示径向、轴向、环向；rz 为剪应力；ν、ν分别表示质点振动的径向和轴向速度。

1.3 初始条件

在给予激振力之前，整个系统是处于静止状态的。因此，系统的速度与应力均为零。

1.4 边界条件

1.4.1 桩顶边界条件

当桩顶受到轴向激振力时，桩顶边界条件为：

其中，

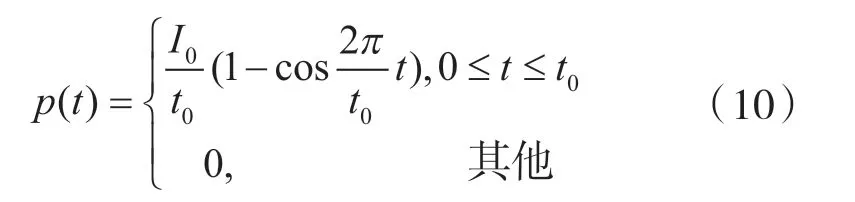
式中，I、t、r分别是激振力的冲量、作用时间和作用半径。

1.4.2 轴对称条件

1.4.3 人工边界条件

本文采用远置人工边界，人工边界与桩之间的距离至少为桩侧土最大纵波波速乘以波在桩中传播两倍桩长所需时间，以确保人工边界的反射波不会对有效信号产生干扰。

2 波动方程的差分离散

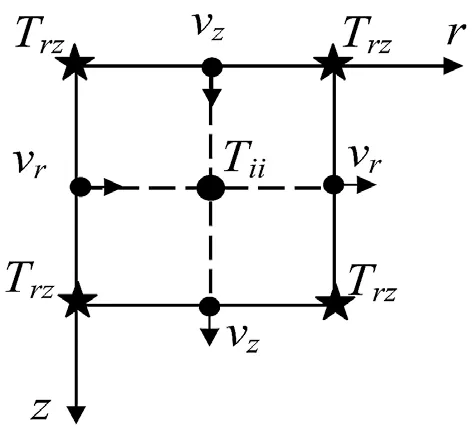
图2 计算单元上分量的交错分布图

本文采用了交错网格差分法，具体的差分离散见图2 所示，通过把应力和速度分量定义在不同的网格系统中（v、v表示质点的振动速度；T表示剪应力；T表示正应力，ii 表示rr、θθ、zz），解决了波动方程中应力和速度的不连续性。通过交错网格差分法对波动方程（1）～（6）进行差分离散，得到如下差分方程：

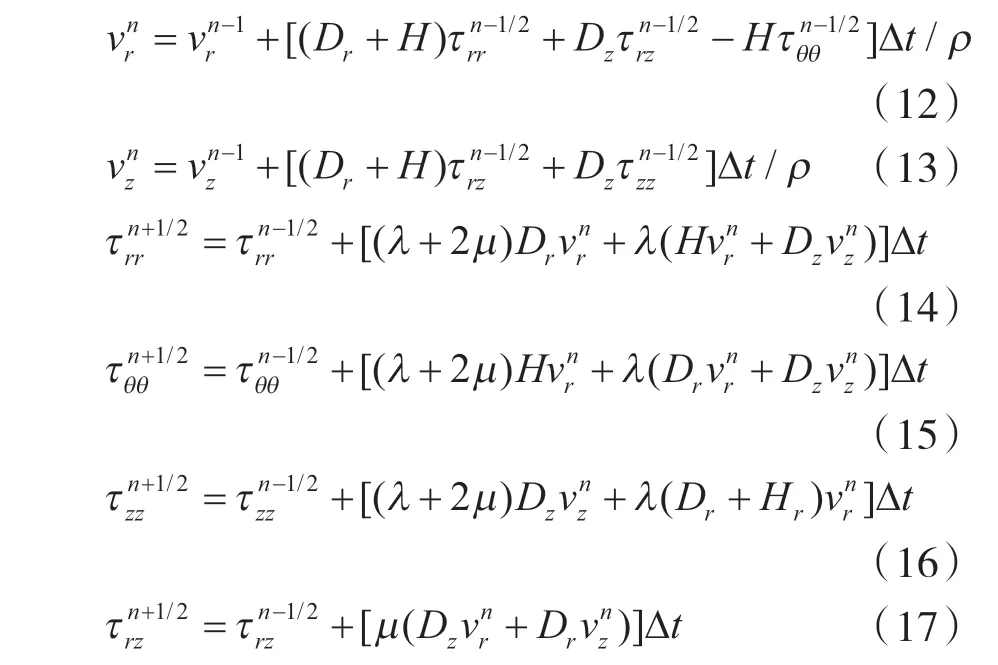
式中，D、D分别为径向和轴向的差分算子；H为平移算子。为了确保材料界面速度和应力的连续性，将计算点上的ρ、μ 按照下式进行处理：

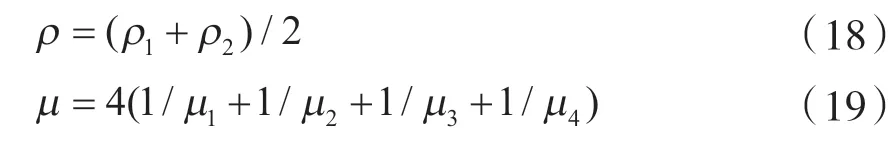
其中，ρ、ρ是计算点邻近两个采样点的密度；μ、μ、μ、μ为计算点邻近四个采样点的剪切模量。

3 数值计算分析

3.1 数值验证

根据上述算法，编制Matlab 计算程序，得到桩身不同点的动力响应曲线。为了验证该方法研究高桩低应变检测的可行性与可靠性，本文将该方法与高桩实测曲线进行对比。桩长为6 m，桩的半径为0.5 m，外露桩长为3.5 m。ρ=2450 kg/m，v=0.28，E=3.35405×10N/m；ρ=2100 kg/m，v=0.31，C=500 m/s；I=1 N·s，t=1 ms，r=4 cm，Δr=1 cm，Δz=2 cm，Δz=2µs。桩周土参数如表1所示。拾振位置采用柯宅邦的0.55R。从图3中可以看出，该方法模拟的桩顶速度曲线与高桩实测桩顶速度曲线具有较好的一致性。从而验证了本文方法的可行性与可靠性。值得注意的是，本文的数值计算得到的曲线具有高频干扰。

表1 桩周土参数Table 1 The parameters of surrounding soil

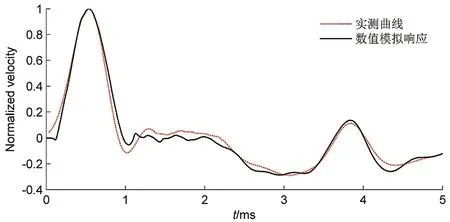
图3 高桩实测曲线和模拟曲线的对比

3.2 高桩的三维干扰

以下文中参数设置为：桩长为10 m，桩的半径为0.4 m。ρ=2400 kg/m，v=0.28，E=3.1104×10N/m；ρ=1900 kg/m，v=0.35，C=200 m/s；ρ=2000 kg/m，v=0.34，C=230 m/s；其他参数和3.1 节一致。

为了更加明了地观察应力波在高桩中的传播，图4 给出了不同时刻的高桩纵剖面波场快照图。当t=0.2 ms 时，入射波以球面波的形式在桩顶附近传播。当t=0.5 ms 时，入射波以平面波的形式向下传播，并在t=0.9 ms 左右时，应力波传至桩入土的界面。当t=2.2 ms 时，应力波在入土桩中继续向桩底传播，同时应力波向桩侧土传播。应力波在t=3.0 ms 左右到达桩底，并在桩底产生反射和透射，从图4（f）-图4（g）可以看出，产生的反射波向桩顶传播，透射到桩底土中的应力波在桩底土中继续传播。当t=6.1 ms 时，桩底反射波到达桩顶。

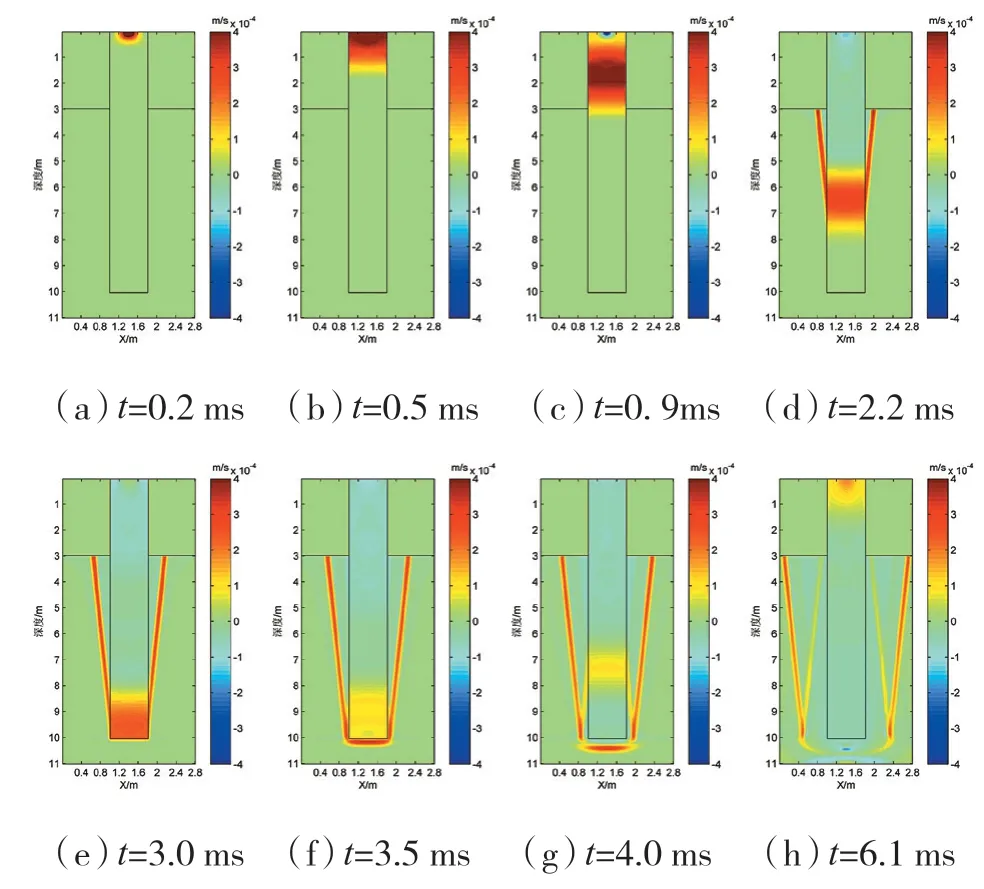
图4 高桩的竖向速度的波场快照图

3.3 最佳拾振位置

与全埋入桩相比，由于高桩存在外露桩长，应力波在桩周产生的反射必然强于全埋入桩产生的反射。为了得到高桩的最佳拾振位置，本文研究了不同外露桩长的不同拾振位置。图5 是外露桩长为3 m 时，桩顶不同拾振位置采集的曲线。首先将在R=0.4 R，0.6 R，0.8 R 三个位置采集的曲线进行对比（Rt 是拾振位置与桩心的距离），从图5（a）中可以发现，当R=0.6 R 时，曲线最为平缓，此时曲线受到的干扰最小。为此，再将R=0.6 R 附近的其他点采集的曲线进行对比。从图5（b）中可以看见，当R=0.6 R 时，曲线最为平缓，此时曲线受到的干扰最小。因此，对于外露桩长为3 m 的高桩来说，低应变采集曲线的最佳拾振为0.6 R。采用同样方法，本文研究了其他不同系列的高桩（桩径不同、桩长不同、L/L 不同），得到了同样的结论。因此，对于高桩而言，低应变最佳拾振位置为0.6 R，此结论既与柯宅邦提出的全埋入桩的最佳拾振位置0.55 R 相区别；也与陈凡提出的2/3 R不同。本文以下研究的拾振位置均采用0.6 R进行采样。

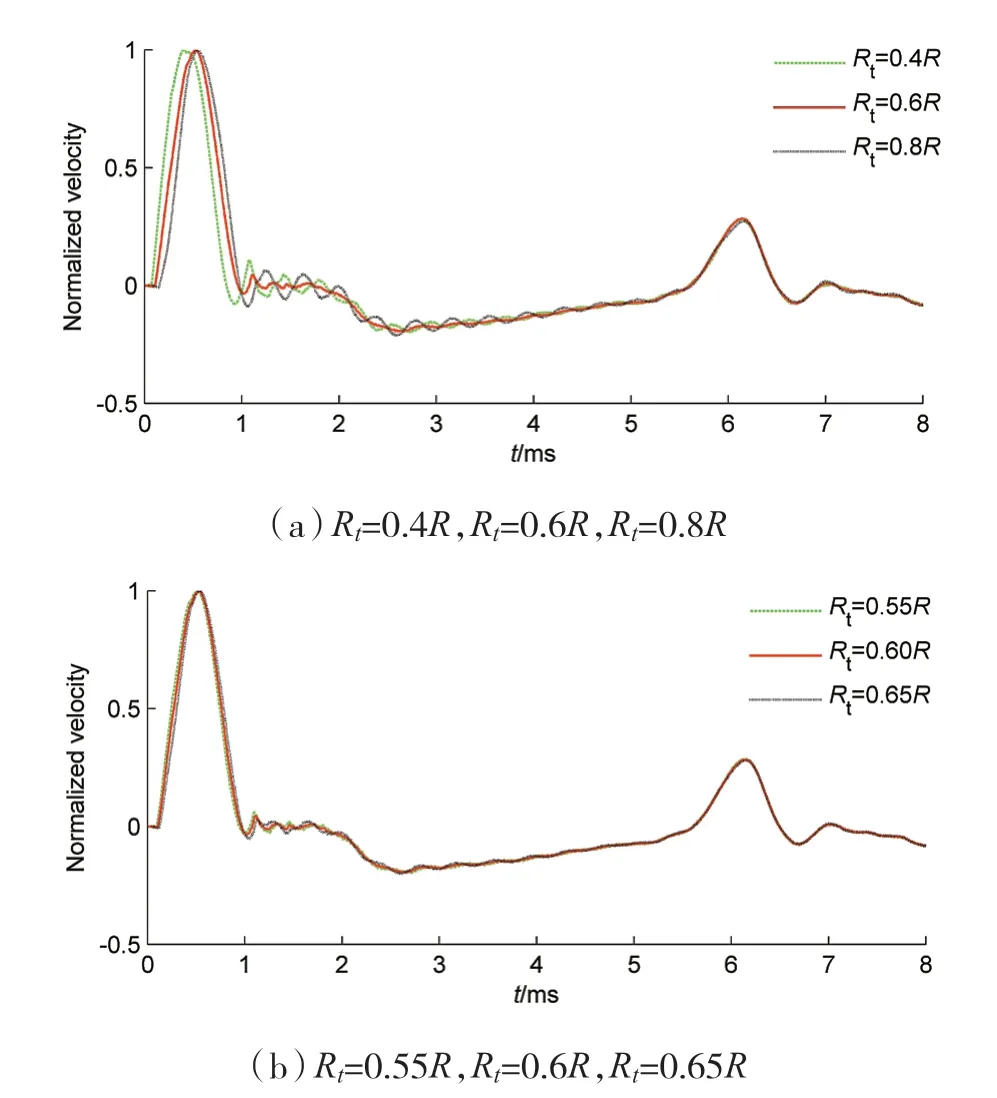
图5 高桩桩顶不同位置竖向速度曲线对比

3.4 高桩与全埋入桩的比较

图6 显示了高桩与全埋入桩的区别。从图中可以看出，高桩在入射波之后有一段零值区，这是高桩有外露桩长，无桩周土作用造成的；而全埋入桩由于存在桩周土作用，桩周土土阻力产生的上行压力波使得曲线为负值。同时，高桩桩底反射波幅值比全埋入桩底反射幅值大。这是由于高桩具有外露桩长，使得能量耗散较少。

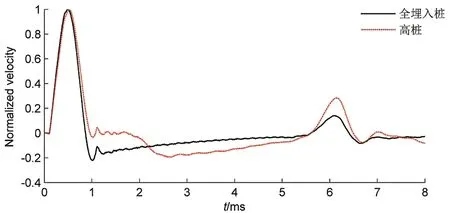
图6 高桩与全埋入桩桩顶竖向速度对比

3.5 外露桩长的影响

图7 揭示了外露桩长对高桩低应变测试的影响。从图中可以看出，随着外露桩长增长，入岩（土）信号推迟。这是因为外露桩长越长，桩周土作用于桩身的长度越短。因此，入岩（土）信号推迟；能量耗散越少。

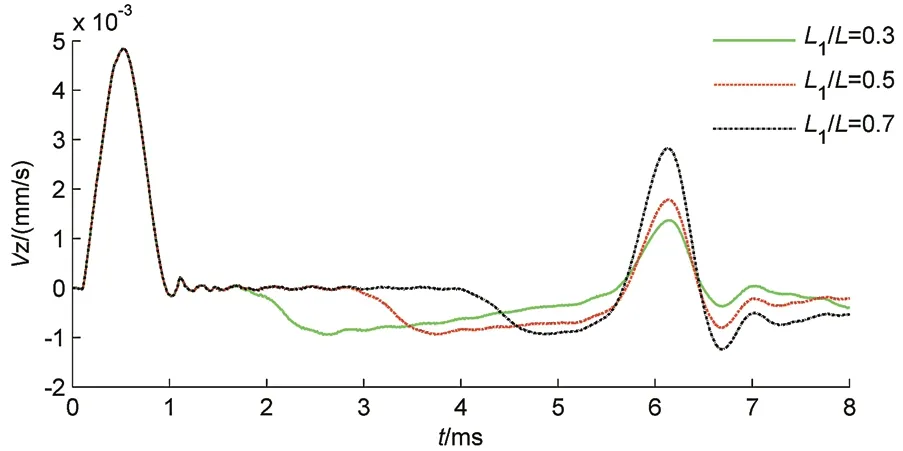
图7 外露桩长对高桩桩顶竖向速度的影响

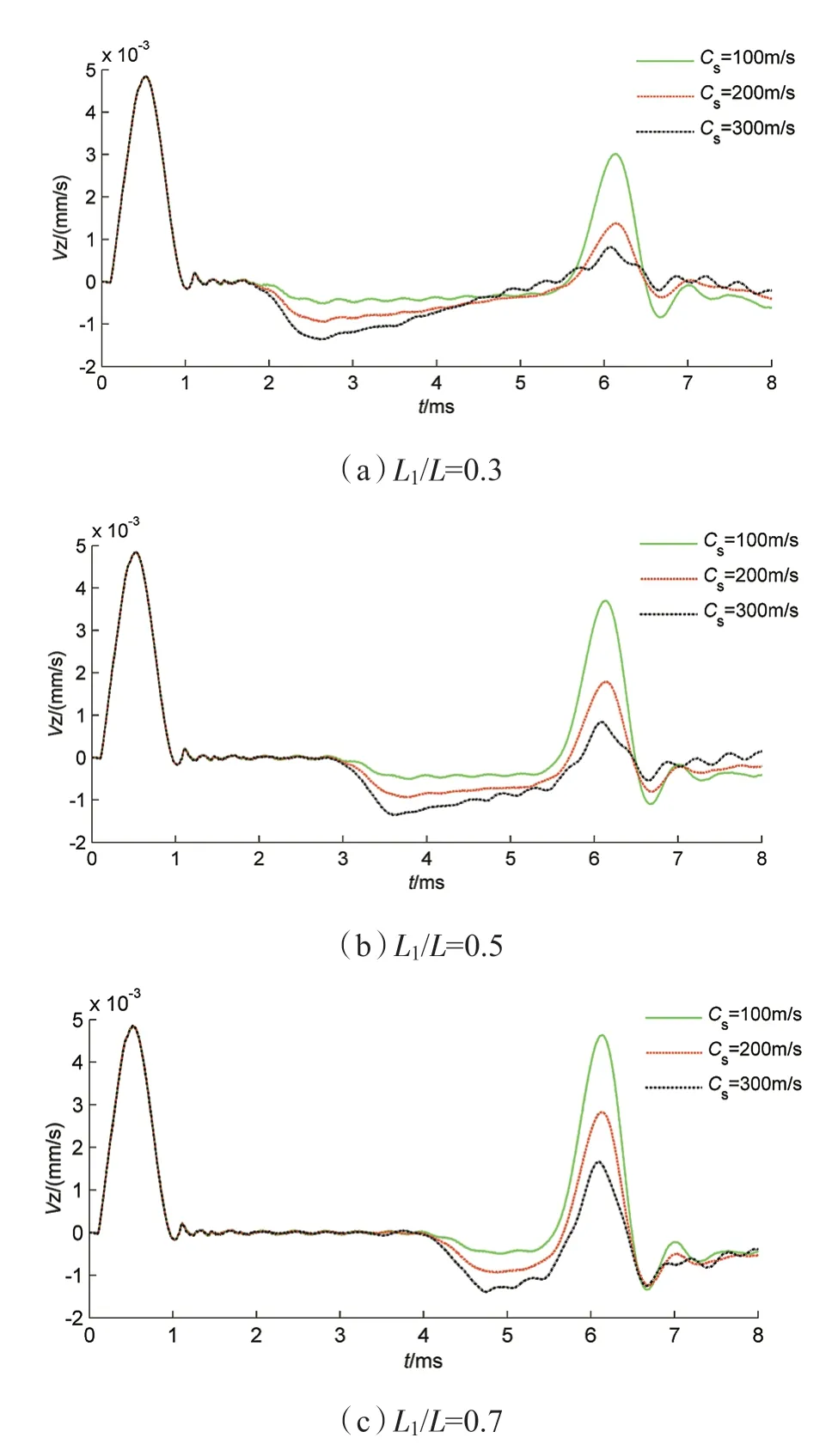
图8 桩周土对高桩桩顶竖向速度的影响

3.6 桩周土的影响

本文分析了桩周土对高桩低应变检测的影响。从图8 可以看出，无论L/L 为多少，桩底反射波随着桩周土剪切波速的增大而降低，这是因为桩周土剪切波速增大，桩中的能量透射到桩周土中的能量越多，致使桩底反射能量变弱。从图中还可以看出，桩周土剪切波速增大，在高桩入土界面处的入岩（土）反射信号越明显，这是因为桩周土剪切波速越大，桩周土越硬从而使得入岩（土）反射越明显。

4 结论

（1）本文建立了高桩的三维轴对称计算模型，运用交错网格有限差分法编制了相应的计算程序，并与高桩实测曲线进行对比，验证了该模型与算法的可行性与可靠性。

（2）给出了高桩桩土系统应力波传播的波场图，直观地反映了应力波在高桩中传播及应力波透射到桩周土及桩底土的过程。

（3）由于高桩存在外露桩长，三维干扰更为强烈。通过对比研究，发现在0.6R 处三维干扰较小。因此，高桩的最佳拾振位置为0.6R。

（4）高桩与全埋入桩相比，具有明显的入岩（土）信号。随着高桩外露桩长的增长，入岩（土）信号推迟；桩底反射信号越强。

（5）随着桩周土剪切波速的增长，入岩（土）信号越明显；桩底反射信号越弱。