重复性及分辨力引入的不确定度分析
2021-06-07李银龙韩帅杨昱刘长海
李银龙 韩帅 杨昱 刘长海


摘 要:运用贝塞尔公式进行A类不确定度评定时,通常包含了重复性和分辨力引入的不确定度分量。文章以FLUKE 5700為标准,将Agilent 34401作为被校准仪表,对其进行不确定度评定,并讲述了重复性引入的不确定度与分辨力引入的不确定度之间的关系。以此为基础,进一步讨论了重复性引入不确定度的读数方法,以及多功能、多量程数字式仪表如何确定分辨力引入的不确定度。
关键词:重复性;分辨力;数字式仪表;A类不确定度
中图分类号:TH701 文献标识码:A文章编号:2096-4706(2021)24-0169-04
Abstract: When the Bessel formula is used to evaluate the type A uncertainty, the uncertainty components introduced by the repeatability and resolution are usually included. This paper takes FLUKE 5700 as the standard, and uses the Agilent 34401 as the calibrated instrument which is evaluated its uncertainty, and describes the relationship between the uncertainty introduced by repeatability and the uncertainty introduced by resolution. Based on this, the numerical reading method of the uncertainty introduced by repeatability and how the multi-function or multi-range digital meters determine the uncertainty introduced by resolution are further discussed.
Keywords: repeatability; resolution; digital instrument; type A uncertainty
0 引 言
进行设备测量时,经常会使用多次测量求平均值的方法来获取设备的“真值”,然而测量设备受方法、仪器、人员、环境等多种因素的影响,会出现食指误差,所以要定期对测量设备不确定去进行评定,以确保测量经常处于良好状态。
在进行不确定度评定时,经常运用A类不确定度或B类不确定的评定。通常情况下,A类不确定度包含了仪器本身分辨力对测量结果造成的影响,因此当我们进行不确定度评定时,不能重复计算,防止评定结果过大。
1 测量结果不确定度来源
对仪器性能指标测量方法进行深入的研究,建立测量模型。分析测量过程,确定不确定度的影响因素,进而转换为不确定度分量。
测量结果的不确定度一般应包含五个部分:(1)测量标准设备本身的不确定度;(2)被检件带来的不确定度;(3)上级测量标准引入的不确定度(测量标准设备溯源引入的不确定度);(4)各种环境因素引入的不确定度,包括温度、湿度等因素;(5)标准设备与被测件的连接系统带来的不确定度,包括失配误差、转接头测量误差带来的不确定度等。可能影响测量不确定度影响因素很多,测量结果不确定度评定考虑的影响因素如图1所示。
2 不确定度评定中各影响因素中之间的关系
下面以直流稳压源标准装置的标准设备Agilent 34401测量标准不确定度评定为例进行说明。以DO30B多功能校准源作为Agilent 34401重复性测试、稳定性考核的测试对象。测试连接图如图2所示。
待测数字多用表的示值误差Ex,考虑各种因素对多用表测量值的影响,其测量模型为:
Ex=Vix+δVix-Vs-δVs
式中:
Vix——DO30B输出电压值;
δVix——DO30B多功能校准源有限分辨力对测量结果影响;
Vs——数字多用表所测得的标准电压值;
δVs——由于多种原因对数字电压表电压值的影响,多种原因包括:上次校准以来标准源电压值漂移;环境对标准源电压值的影响;Agilent 34401的极限允许误差等。
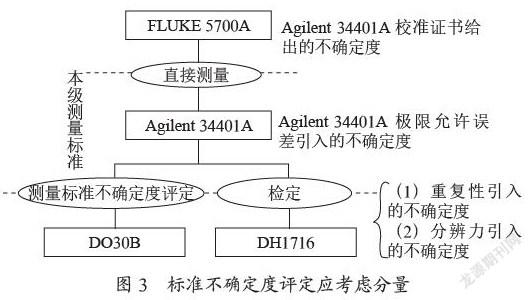
图3表明了直流电压检定标准设备Agilent 34401A的测量标准不确定度评定应考虑的不确定度分量及相互关系。
2.1 重复性引入的不确定度与分辨力引入的不确定度
由它们引入的测量不确定度应体现了随机效应对数字表测量分散性的影响,体现了测量标准本身的测量固有能力,因此可以理解为由随机误差引入的不确定度分量,当重复性引入不确定度分量大于4倍分辨力引入的不确定度分量,只需考虑重复性引入的不确定度分量;当被测标准源稳定性很好,则只需考虑分辨力引入的不确定度;如果两个数值比较接近,则平方和相加,由于两类不确定度性质相似,存在相互包含关系,现在通常的做法是取大的。
2.2 测量标准引入的不确定度分量
主要包括两个方面:一是上级测量标准引入的不确定度分量,它反映了不确定度的传递性。是上级测量标准对本级测量标准进行检定的测量结果不確定度;二是本级测量标准的极限允许误差引入的不确定度。
3 示值误差与测量结果不确定度各分量之间的关系
示值误差=示值-真值
由于真值不能确定,所以一般情况下取高一级测量标准所复现的值为“真值”,实际上叫作约定值或者叫校准值、标准值。即:
示值误差=示值-校准值
重复测量时,示值的分散性不尽受到测量设备的随机效应影响,同时测量仪器本身的分辨力也会影响测量结果。
一般运用贝塞尔公式进行A类不确定度评定时,被测件的分辨力已经包含在测量结果之中,因此重复性可不用考虑分辨力引入的不确定度,但由于部分测量设备使用时间较久、稳定性不好造成分辨力太大时,由贝塞尔公式计算的得到的不确定度,分辨力引入的不确定度远远大于重复性引入的不确定度,所以应当用分辨力引入的不确定度来代替重复性引入的不确定度。图4为示值误差与测量结果不确定度各分量之间的关系。
4 重复性引入的不确定度分量读数方法的分析
对于多功能数字表来说,由于其测量参数多,不同参数、不同量程分辨力也不一样。如果测得的数值最末几位数一直在跳变。就要对跳变的显示值进行读数,下面分以下两种情况进行分析。
4.1 读数值没有变化或者跳变范围很小
数字表读数一直非常稳定,没有变化,直接读数即可,如果读数一直在两个数之间跳变,则大概按照跳变的比例关系,读出数值。数字表读数的平均值与标准表的差值反映的是系统误差的大小,而数字表读数的重复性反映的是测量结果的离散程度,反映的是系统随机误差的大小。
下面以FLUKE 5700为标准,Agilent 34401A为被校准仪表,进行重复性测试。短时间内,由FLUKE 5700多功能标准源输出直流10 V标准电压,用数字多用表Agilent 34401A进行多次测量,数字多用表的示值测量结果如表1所示:
在20 ℃±1 ℃条件下,被校准数字多用表10 V点示值误差为Ex=(0.000 04±0.000 05)V。
因此0.000 04 V反映了系统误差影响量大小,±0.000 05 V反映了随机误差影响量大小。
4.2 读数一直在无规律地跳变
读数在一定范围内无规律地跳变,在记录重复性数据时要尽可能记录变化范围的边界点数据,而不应该是只选择测量误差比较小的数据,或是随机选取测量结果。采用这种读取数据方法主要考虑以下两方面的原因。
第一,测量数据的边界点更能够反映出两个不同的表的性能差异,而中心点的数据则反映不出性能的差别。例如,两种不同型号的枪支A、B,相同的距离进行n发子弹的射击,进行重复性的测试。子弹弹孔在靶上的分布图如图5所示。显然边界点的数据更能反映两个枪的性能差异。
第二,读取边界点的数据保证了不会把重复性引入的不确定度值评定小了,重复性引入的不确定度增大会导致相应的扩展不确定度也相应增加,使评定的不确定度更客观反映测量结果的实际情况。不会使本来不合格的结果被判定合格,造成不必要的损失。
5 分辨力引入不确定度的分析
下面以数字多用表检定为例说明多功能、多量程数字式仪表如何确定其分辨力。例如用FLUKE5700作为标准源,输出交、直流电压10 V,对Agilent 34401数字多用表进行校准,仪器连线如图6所示。
通常计算分辨力引入的不确定度方法如下:无论是直流还是交流10 V点,6位半的数字多用表显示最末一位表示10 μV电压,因此每个读数值可能包含的误差应在±5 μV范围内。假定其在该范围内满足矩形分布,于是所引入的不确定度分量为:
在直流10 V点,交流10 V,1 kHz点,FLUKE 5700标准输出不同的电压值用以检验Agilent 34401在该测量点的分辨力。数字表分辨力测试数据如表2所示。
从上面的检定数据可以清楚地看出,如果按照通常做法,将数字表Agilent 34401最后一位数字作为分辨力。直流10 V点测量数据没有问题,而在交流10 V、1 kHz点显然分辨不到10 μV,仅能稳定地分辨到1 mV,也就是说在测量结果不确定度评定过程中由分辨力引入的不确定度被估计小了两个数量级,造成了测量结果不确定度评定值偏小。
一般情况下,对于单一测量功能的仪表来说,分辨力正常情况下可以认为数字式仪表最末一位的数字区间半宽度代表的量值。但是对于数字表这样具有多参数测量功能的仪表来说,在精度不是最高的功能、量程上,最末一位的数字区间半宽度可能代表不了数字式仪表的分辨力。
6 结 论
因为重复性引入的不确定度分量与分辨力引入的不确定度存在包含关系,因此在测量结果不确定度评定中,应注意二者的选取方法。另外,在测量过程中注意进行重复性测量时测量数据的读数方法以及多功能数字式仪表不同参数、不同量程分辨力的确定方法等问题,以免使测量不确定度评定结果与实际情况偏差较大。
参考文献:
[1] 姚尧,田郁郁,王志鹏,等. 可燃气体报警器示值误差测量结果的不确定度评定 [J].低温与特气,2018,36(4):40-42.
[2] 孙立军,党士忠,张涛,等.流量计性能受流量稳定性影响实验 [J].天津大学学报(自然科学与工程技术版),2018,51(4):422-432.
[3] 倪育才.实用测量不确定度评定 [M].北京:中国计量出版社,2010.
[4] 黎清容,宋婧. 实验室测量系统的准确度评价方法 [J].广东建材,2021,37(7):42-44.
[5] 罗雪梅,张淑芳,夏继军,等.对分辨力与分辨率用法之浅见 [J].编辑学报,2012,24(S1):26-27.
[6] 卫兵,卿燕玲,傅贞,等.脉冲高电压幅值测量的不确定度分析 [J].强激光与粒子束,2009,21(10):1561-1565.
作者简介:李银龙(1983.09—),男,汉族,河南平顶山人,助理工程师,本科,研究方向:电抗技术。
