小口径低温文丘里流量计流动性能的数值分析
2021-06-06刘耕田李俊杰欧阳峥嵘匡大志艾陈旭恒
刘耕田 李俊杰* 欧阳峥嵘 石 磊 匡大志艾 鑫 方 明 陈旭恒
(1 中国科学院合肥物质科学研究院 合肥 230031)
(2 中国科学技术大学 合肥 230026)
1 引言
低温流体流量的准确测量对于低温系统的稳定运行具有非常重要的意义。常见的低温流量计有:节流流量计(包括孔板流量计、喷嘴流量计和文丘里流量计)、涡轮流量计、超声波流量计及质量流量计等。对于磁场环境液氦温区下的流量测量又有特殊要求,而文丘里流量计满足这种环境下流量测量广泛的温度适用范围、高密封性、耐压性、较低的压力损失、对磁场的低灵敏度等要求,同时文丘里流量计结构简单、价格低廉、不易损坏,因此成为低温流量测量最适用的流量计。ISO5167-4 对50—1 200 mm 管径的文丘里流量计的结构、制造、性能等均有说明,对于50 mm以下的小口径文丘里流量计并未涉及,同时,国内对77K 以下的文丘里流量计的性能研究较少。
关于差压式流量计的研究工作主要集中于流出系数和压力损失两个方面,前者代表着实际流量与理论流量之比,后者意味着文丘里管造成的永久压力损失。对于差压式流量计而言,期望测量所需的差压信号越大越好,节流件所带来的压力损失越小越好,从节能和经济的角度出发,仪表的压力损失对于仪表的选型有着重要的参考价值,但是单一的差压信号无法衡量一个装置的优劣性,因此,引出压力损失比这个指标,简称压损比,它定义为节流件的压力损失与测量的差压的比值[1]。中国科学院等离子体物理研究所的朱志刚[2]、孟春亚[3]等人对小口径低温文丘里流量计进行了常温下的测试与数值模拟,分析了文丘里结构参数对流出系数和永久压损的影响,通过正交数值模拟实验确定了一种性能较为优秀的文丘里结构以及通过实验确定了一种规格的小口径文丘里流量计的流出系数和精度。Süßer M.,JitschinW[4]等人通过实验得到了一种小口径低温文丘里流量计的流出系数与喉部雷诺数的拟合公式。
针对低温下流体测量的准确性、能量损耗、紧凑性等要求,中国科学院强磁场科学中心大科学装置低温系统中的文丘里流量计的尺寸以10 mm 左右最为合适,本文以现有10 mm 低温文丘里流量计为基础,利用CFD 工具,以氦气为流体介质,给出了4.5 K 温度下该文丘里流量计流出系数随雷诺数的函数关系,有助于后续实验误差的分析和文丘里流量计精度的校准,在此基础上分析了喉径比、收缩角度对流出系数和压损比的影响,为优化小口径文丘里流量计结构提供方向性参考。
2 文丘里流量计工作原理
文丘里流量计由入口圆筒段、圆锥收缩段、圆筒喉部、圆锥扩散段和出口圆筒段4 个部分依次连接组成。其结构如图1 所示。其中圆筒段管道内径为D,圆锥收缩段收缩角度为α,喉部长度为l,喉部内径为d。
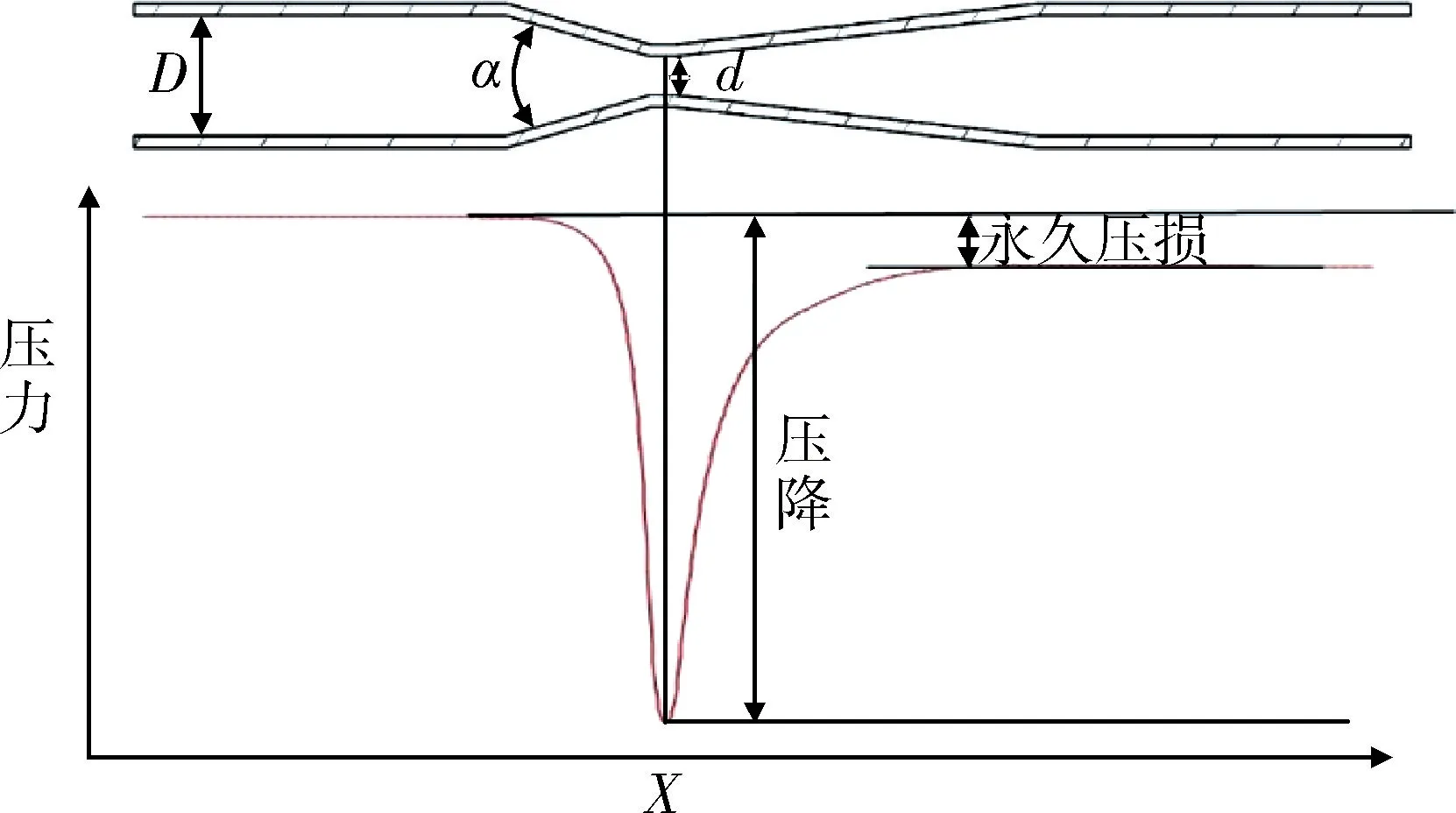
图1 文丘里管结构和压力分布图Fig.1 Schematic presentation of Venturi tube and pressure distribution
文丘里流量计测量的原理与其它差压式流量计相同,即伯努利方程和流动连续性方程。在流体流经文丘里流量计时,在喉部区域由于管径的变化,流体流速增大,静压降低。如图1 所示,通过测量入口处的静压与喉部位置的静压之差,即通过压降或者说差压来确定流量。由伯努利方程和流动连续性方程推导的流体质量流量qm与压降Δp关系:
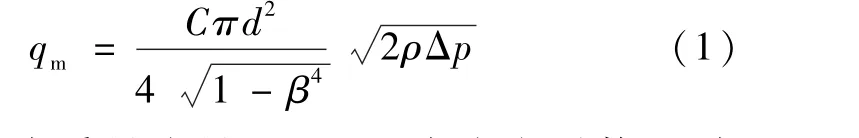
式中:qm为质量流量,kg/s;C为流出系数;d为喉部内径,m;β为喉径比,即喉部内定d与管道内径D之比;ρ为流体密度,kg/m3;Δp为压降,Pa。
同时压损比ζ 与压降Δp关系:

式中:pL为永久压力损失,即进口压力与出口压力之差,Pa。
3 几何模型与数值模拟方法
3.1 几何模型与网格划分
文丘里流量计的数值仿真区域选取其内部流体域,计算流体域结构如图2 所示。为减少入口效应和出口返流的影响,设置了10D的入口直管段和出口直管段,并保持长径比始终为1(长径比为喉部直径和喉部长度之比)。根据ISO5167-4 及实验用文丘里流量计结构设置文丘里结构参数,表1 展示了实验用文丘里流量计的主要参数,表2 为仿真几何模型的主要参数,NO.2(NO.7)为目前在实验室中的文丘里流量计,另外始终保持文丘里流量计的长径比(喉部长度和喉部直径之比)为1,出口角度始终为8°。利用Mesh 划分六面体结构化网格,并且在喉部区域对网格进行加密处理,整体网格和局部网格见图3。

图2 文丘里流量计计算区域Fig.2 Fluid diagram inside Venturi meter

表1 实验用文丘里流量计的主要参数Table 1 Main parameters of Venturi flowmeter used in experiments

表2 文丘里流量计结构参数(10 mm 管径)Table 2 Dimesions of Venturi tube(inside diameter is 10 mm)
图3 整体网格和局部网格Fig.3 Global and local meshes
3.2 数值求解方法及边界条件设置
4.5K氦气在文丘里流量计内的流动时,密度几乎不发生变化,视为不可压缩流动。考虑到计算精度、可靠性和计算时间,选取标准的k-ε模型进行计算,并采用标准壁面函数进行修正,使用稳态模拟,数值计算采用有限体积法,速度与压力的耦合采用couple 算法。仿真计算中,所使用的边界条件以现有的实验为基础,设置为压力型入口、质量流量型出口及外壁面固定无滑移边界条件。
3.3 数值模型的验证
在保证计算结果准确性的基础上尽可能地缩短计算时间,需要对生成的网格进行无关性验证,确定合适的网格数量。当网格数量达到30 W 后,文丘里流量计沿程压力的计算结果随网格数目几乎不发生变化(偏差低于0.028%),表明此时网格数已经达到计算要求,图4 展示了距文丘里管入口0.09 m 至距离文丘里管入口0.12 m 区域(此区域压力随网格数目的变化最大)的沿程压力随网格数目的变化情况,因此在仿真计算中采用的网格数量在30 W 左右即可。
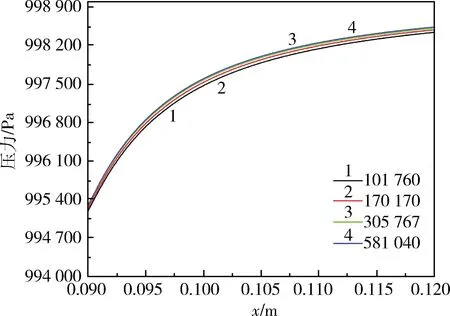
图4 不同网格数量下文丘里流量计的沿程压力变化曲线Fig.4 Pressure curve of Venturi flowmeter with different grid numbers
选用的标准k-ε模型已有中国科学院等离子体物理研究所的孟春亚[3]等验证过其在低温下的准确性,本文以实际实验结果进行进一步的验证,实验文丘里管参数已经在表1 中给出,图5 给出了流出系数C的模拟结果和实验结果对比情况,偏差小于6%,并且随着雷诺数的增加,偏差进一步减小。

图5 实验和数值模拟得到的C-Re 对比关系图Fig.5 Comparison between C-Re curves obtained by experiment and numerical simulation
4 结果分析与讨论
在完成模型验证后,以氦气为流体介质,进口温度为4.5 K,进口压力为10 ×105Pa,利用HEAPAK查得对应密度为148.224 4 kg/m3,动力粘度为4.656 97 ×10-6Pa·s,对表2 中所列的不同结构参数的文丘里流量计进行模拟与分析。
4.1 流出系数与雷诺的关系
在文丘里管结构及安装方式确定后,流出系数C为喉部雷诺数Re的函数,即C=F(Re)。通过改变氦气质量流量,计算得到不同雷诺数下的流出系数。参考了多个拟合函数,包括Süßer M[4]等人通过实验提出的对数形式的方程以及Reader-Harris M J[5]在文章中提及的包含指数形式的多个方程,最终确定的目标函数形式为C=a+b×Re-0.5,流出系数与喉部雷诺数的关系拟合公式如式(3),拟合曲线如图6所示。

从图6 中可以看出,流出系数的值随着喉部雷诺数的值增加而增加,当雷诺数较低时,流出系数的值增加得很快,而当雷诺数到达一定数值后,流出系数的值增加较为缓慢,增加幅度越来越小。这一变化规律符合牛顿流体的性质,随着雷诺数的增加,流体粘性对流场的影响越来越小,由粘性引起的边界层越来越薄,惯性力的作用开始远远大于粘性力的作用,从而计算而得的流量越来越逼近真实值,流出系数越来越接近1,也可以说,抛开制造安装等因素,流出系数是对粘性作用的修正。
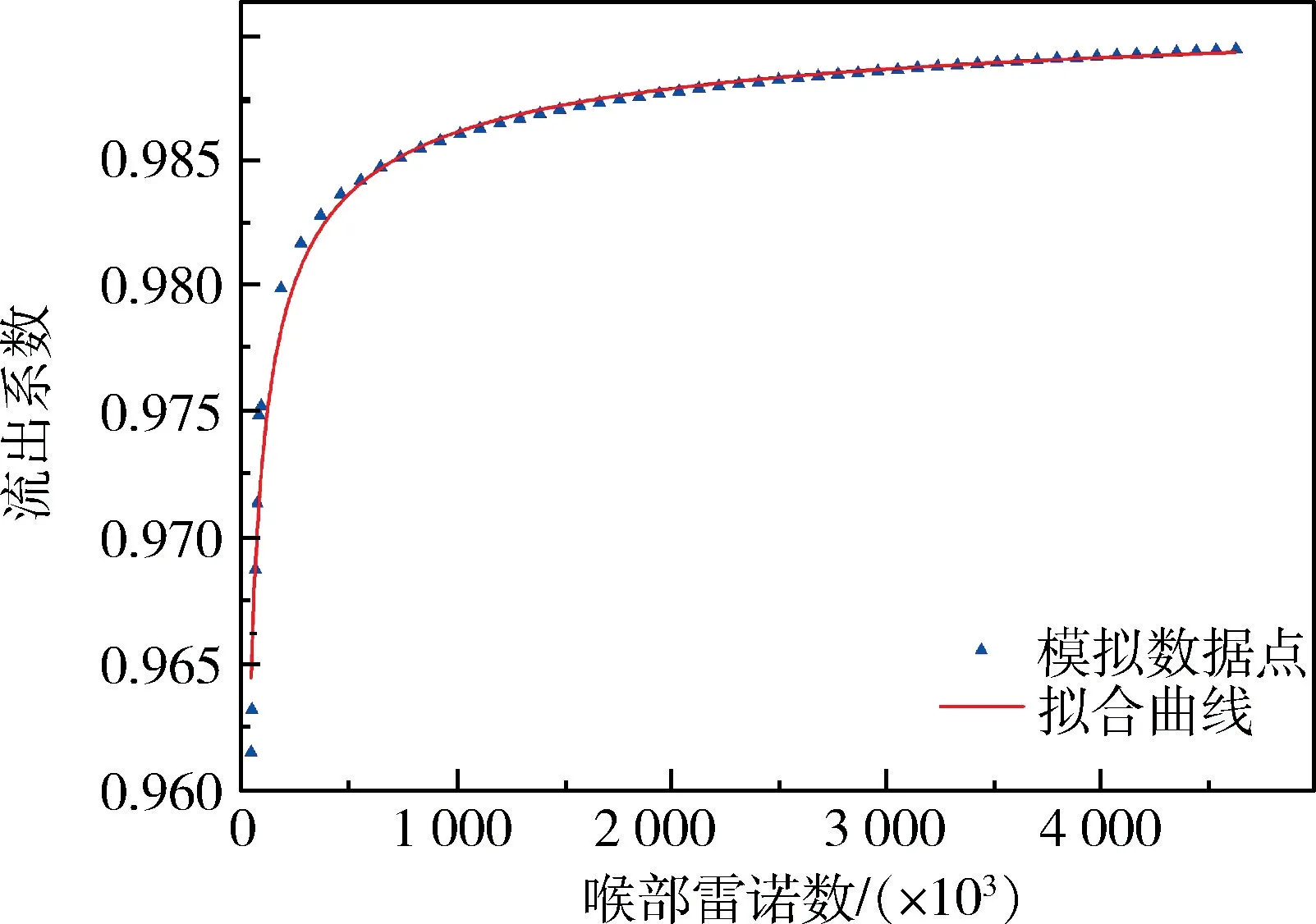
图6 拟合曲线Fig.6 Fitted curve
4.2 喉径比对流出系数和压力损失比的影响
图7 给出了不同喉径比文丘里流量计的流出系数C和压损比ζ。从图中可知,对于确定结构的文丘里流量计,随着雷诺数增大,流体流动受粘性影响越来越小,流出系数逐渐变大,在雷诺数小于106时变化非常剧烈,随着雷诺数进一步增大,流出系数变化逐渐平缓,最终流出系数趋向一稳定值,同时压损比ζ 也在逐渐减小;而随着喉径比的增大,在喉部区域边界层的厚度相对于整个管道变薄,因此流出系数C相对增大,而同时由于喉径比增大造成收缩段长度变大,导致了额外的压力损失,所以压损比ζ 在一定范围内相对增大。不同喉径比会对氦气在文丘里流量计内的流动产生不同程度的阻碍,由图8 所示的文丘里流量计在氦气质量流量为10 g/s 时的速度云图可以看出,随着喉径比的减小,氦气流动速度在喉部区域发生的变化越剧烈,同时,因为流体的惯性使得流束经过喉部入口后有射流现象,在距离喉部入口一定位置流体速度达到最大值。
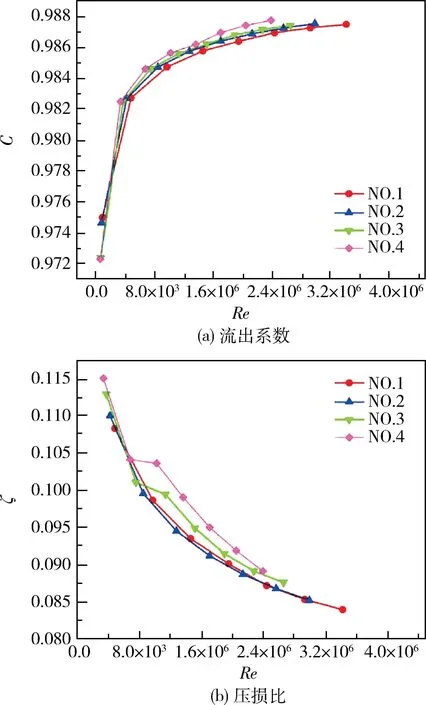
图7 不同喉径比文丘里流量计的流出系数和压损比Fig.7 Discharge coefficient and pressure loss ratio of Venturi flowmeter with various β values
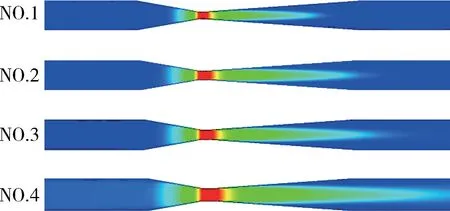
图8 10 g/s 氦气流经不同喉径比文丘里流量计内流动的速度云图Fig.8 Velocity contour of He in Venturi flowmeters with various β value at 10 g/s
4.3 收缩角度的影响
进口锥角同样会影响着流体流经文丘里流量计的流动状态,结合标准确定了表1 中NO.5 到NO.10五种规格不同收缩角度的文丘里流量计。不同收缩角度的文丘里流量计的流出系数C和压力损失系数ζ随雷诺数的变化如图9 所示。可以看出,进口锥角为20°的文丘里流量计的流出系数明显大于18°、16°的文丘里流量计的流出系数,而20°、22°、24°的文丘里流量计流出系数随雷诺数的曲线几乎完全重合,也就是说,当达到20°以后,小范围的进口锥角度数的变化对流出系数几乎不产生影响,同时,压损比随着收缩角度的增大而减小。图10 给出了不同收缩角度的文丘里流量计内部氦气流动的速度云图,可以看到,随着收缩角度的增大,氦气流动速度在喉部区域变化得更快一些,同时,可以看到氦气在文丘里管内的流动情况随着收缩角度改变的变化远远小于随着喉径比改变的变化。

图9 不同收缩角度文丘里流量计的流出系数和压力损失比Fig.9 Discharge coefficient and pressure loss ratio of Venturi with various α values

图10 10 g/s 氦气流经不同收缩角度文丘里流量计内流动的速度云图Fig.10 Veiosity contour of He at 10 g/s of Venturi flowmeters with various α values
5 结论
通过对4.5 K 低温氦气流经小口径文丘里流量计的流动特性的数值模拟,分析了小口径低温文丘里流量计流出系数与雷诺数的关系以及结构参数对文丘里流量计性能的影响,得到了以下结论:
(1)4.5 K 温度下,10 mm 小口径文丘里流量计的流出系数与雷诺数倒数的平方根成线性关系;
(2)4.5 K 温度下,10 mm 小口径文丘里流量计的流出系数随着喉径比的增大而增大,同时压损比随着喉径比的增大而增大;
(3)4.5 K 温度下,一定范围内,10 mm 小口径文丘里流量计的流出系数随着进口角度的增大而增大,同时压力损失比随着进口角度的增大而减小。
对小口径低温文丘里流量计测量精度提高及结构优化研究,后续实验将进行进一步验证。
